介观尺度下多孔介质内水结冰相界面演化机制研究

王文松，杨英英，2，陈周林，杨晴雨，李帅华，武卫东

（1 上海理工大学能源与动力工程学院，上海 200093； 2 上海市动力工程多相流动与传热重点实验室，上海 200093）

引 言

寒区冻土的自然冻融循环[1-3]、食品冷冻保鲜[4-6]、蓄冰制冷[7-8]等都涉及到水在其内部的固液相变问题，研究多孔介质内水冻结过程的传热传质问题在寒区工程、生物和能源等领域中有重要意义。如在寒区建筑工程中，土壤的冻胀和融沉引起的建筑道路破坏给工程建设带来巨大的经济损失[9-10]。通过对土壤等多孔介质内的相变过程[11]和温度场[12]研究，可提出冻害的预报与防治方法，缓解冻胀带来的危害[13-15]。

目前已有学者通过宏观实验来研究多孔介质内的冻结特性，马钦[16]实验研究了不同颗粒直径与表面温度对多孔介质温度分布与冻结速率的影响。但大部分的宏观热质规律实验研究难以揭示其微观的相变热质传递机理。对此，一些学者通过开展孔隙尺度或介观尺度实验研究多孔介质内水相变热质传递机理。Løvoll 等[17]观测了随机二维多孔介质内两相流驱替现象，验证了渗流理论。Fen-Chong等[18]使用含水玻璃微珠来构建多孔介质，通过电容法来研究冰-水相变过程中两相压力变化。

同时，为了揭示多孔介质内水相变的影响因素及作用机理，一些学者开展了理论与模拟研究。Everett[19]提出毛细理论，认为毛细管在弯曲冰-水界面上产生毛细吸力。Gharedaghloo 等[20]利用孔隙尺度模拟来研究冻融循环时接触角滞后对多孔介质含水率的影响。刘正明[21]模拟了未冻水在不同的冰-土颗粒组成的孔道微尺度模型中的迁移流动，分析了不同粒度组分下未冻水的迁移速度及冻结缘处的渗透率。Gawin 等[22]采用非平衡法模拟水-冰相变来研究多孔介质中水过冷与含水率滞后现象。Wu 等[23]认为冰晶生长的驱动力是基于热力学的不同温度下化学势梯度。Lin 等[24]对纳米颗粒与冰-水界面的相互作用进行了系统的分子动力学模拟，得到由于纳米粒子对界面的钉扎作用，冰-水界面形成凹曲率，抵消了晶体生长的驱动力，导致冰晶生长速度变慢。李伟斌等[25]提出三维微观孔隙结构的建模方法，基于结冰二维定量信息表征三维模型的二维孔隙定量信息，且与实验结果相吻合。

综上所述，目前已有学者开展了针对多孔介质冻结的相关实验与模拟研究，但是从介于微观与宏观之间的介观尺度（μm～mm 级）上对多孔介质内水冻结的相变过程进行的可视化实验研究非常少。本文利用红外热像仪与微距CCD 相机对孔隙尺寸为500 μm 的多孔树脂内水的冻结过程进行实验研究，分析其相界面及温度场的演变规律。并对不同边界温度（-15、-10、-5℃），不同孔隙间距（50～500 μm）,不同孔隙结构（圆形、方形）下的冻结过程进行模拟研究，分析不同冻结边界温度、孔隙间距和孔隙结构对相界面演变规律和水冻结速率的影响，研究温度场驱动的冻结演变机制。

1 理论与方法

1.1 毛细理论模型

在微孔道冻结过程中，水相与冰相的转变与传热均满足连续性方程与导热能量方程。

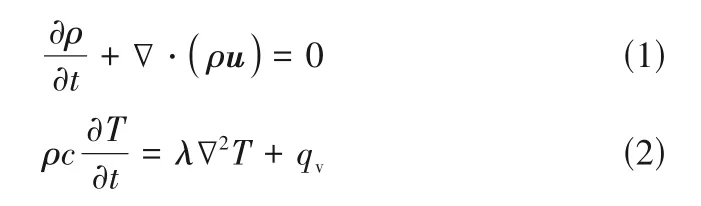
式中，ρ为密度；u为速度矢量；c为比热容；λ为热导率；qv为热源，主要来自相变潜热。

其中未冻水的流动符合不可压缩Navier-Stokes方程。

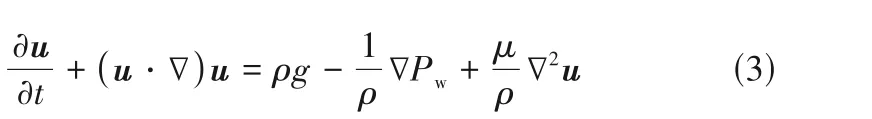
式中，Pw为水压；μ为动力黏度。

当孔道的孔隙半径处于毛细尺度以下时，相界面还受到毛细压力的影响。毛细理论可以描述水冰系统相平衡时水压力、冰压力与温度之间的关系，该理论基于广义Clausius-Clapeyron方程[26]：

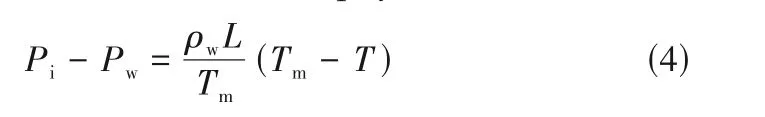
其中，Pi为孔隙冰压；L为水热相变潜热，取值为334.88 kJ/kg；Tm是水的冻结温度，如图1(a)所示。式(4)表明，冻结过程中的温度梯度会影响冻结面上的压力差。在实际情况中，冰的应力张力在各方向上是非均匀性的，式(4)中孔隙冰压Pi为表面应力张量的法向分量。冰水界面上水压力Pcl为：

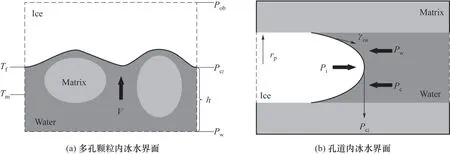
图1 冰-水相界面示意图Fig.1 Schematic of ice-water phase interface

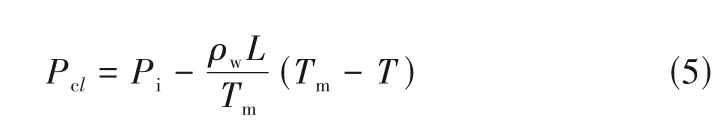
在毛细尺度下，由于压力差导致相界面产生月牙形的弯曲，如图1(b)，该压力差由Young-Laplace方程控制[17]：

式中，γiw为冰水界面的表面张力系数，取值为33×10-3N/m；r为冰水相界面的曲率半径。则孔隙中毛细压力Pc为：

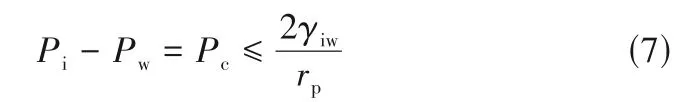
式中，rp为孔隙半径，与多孔介质的孔隙结构和大小有关，因此在不同的孔隙结构中，冻结面演变也不同。联立式（4）和式（6）得到冻结面的温度Tf：

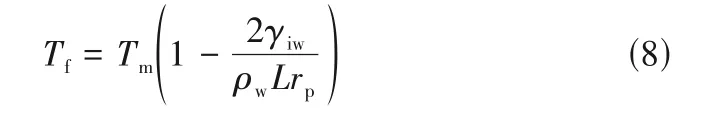
式（8）为Gibbs-Thomson 方程[27]，冰水界面的曲率和温度均受该方程约束。当冻结面温度Tf低于临界温度时，冰水界面的曲率半径小于孔隙半径，则冰层向孔隙中发展，形成向前弯曲的界面，同时相界面中心位置的平衡温度高于界面上其他位置的平衡温度，并且随着相面曲率半径的减小而增大，同时相界面温度并不等于液态水冻结温度，存在一定的过冷现象[28]。

1.2 单向冻结实验研究方法

1.2.1 介观尺度单向冻结实验台 本文通过搭建介观尺度单向冻结实验台，研究孔隙半径为500 μm的微孔道内水冻结过程中温度与相界面的变化，实验台如图2(a)所示。实验台由环境控制及观测两部分组成，其中环境控制部分由恒温水槽、保温箱与冷腔组成，可以保持环境温度稳定和提供指定温度边界。观测部分如图2(b)所示，保温箱上方设置观测孔，通过伸入红外成像仪与微距CCD 镜头的方式观测温度演变与冻结面演变。

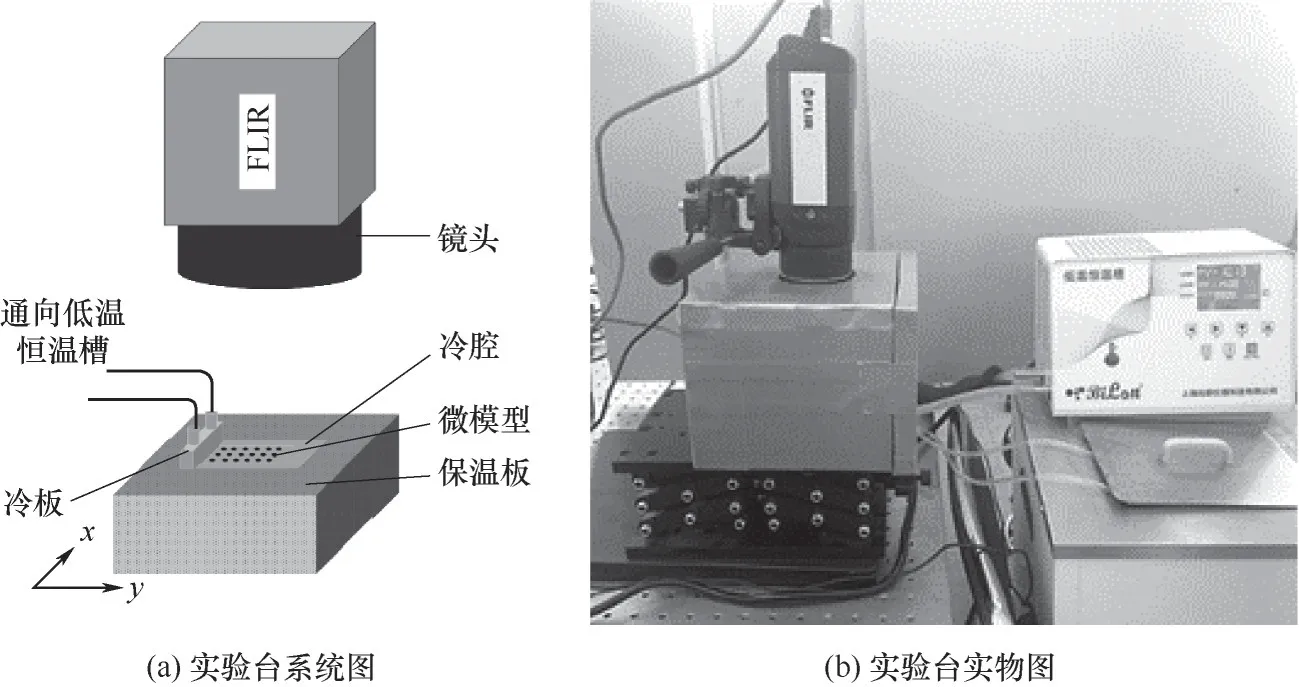
图2 单向冻结实验系统图和实物图Fig.2 System diagram and object diagram of unidirectional freezing experiment

通过进行重复性单向冻结实验，分别对冻结过程中的温度场及冻结面演变进行观测。使用红外成像仪记录整个冻结过程的温度场变化，微距CCD相机拍摄冻结面变化，边界温度Th为-20℃，初始温度T0为20℃。使用仪器及关键参数如表1所示。

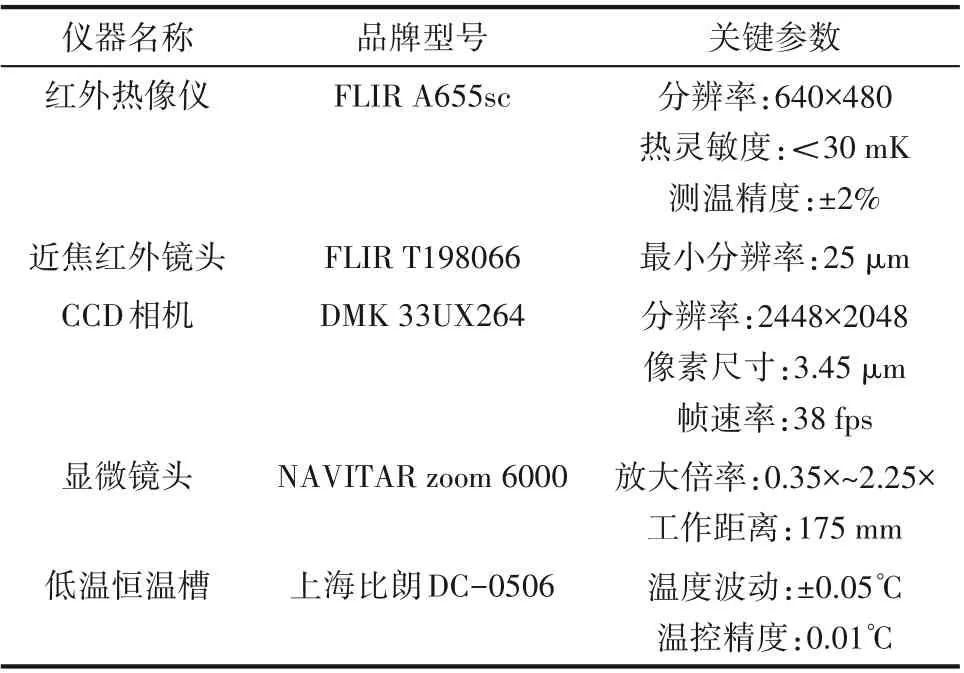
表1 设备相关参数Table 1 Parameters of equipment

1.2.2 多孔树脂微模型 本实验设计了具有二维多孔介质结构的微模型。该模型由树脂3D 打印制成，精度达到10 μm，结构如图3 所示。多孔模型总尺寸为20 mm×10 mm×10 mm，多孔骨架为圆形。如图3(b)，其中的微网格为直径1 mm 的微型圆柱，圆柱间距为500 μm。该模型能从二维角度模拟多孔介质内水冻结过程的特征。底部基底用于支撑孔隙骨架，其高度对实验结果无影响。由于冷板（冷源）温度恒定，热通量不会受到基底高度变化的影响。

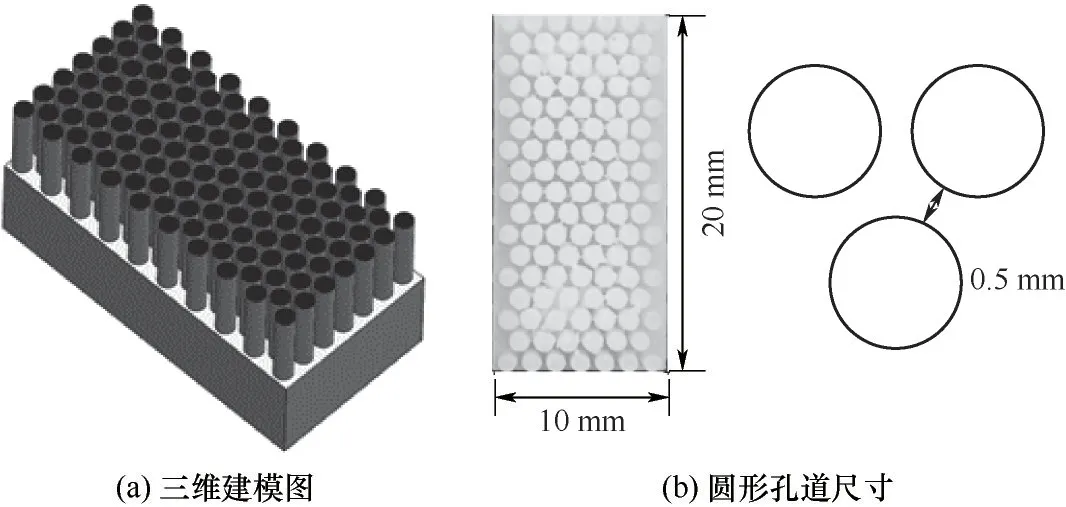
图3 被测多孔树脂微模型结构示意图Fig.3 Structural diagram of the tested porous resin micro model

1.3 模拟研究方法

1.3.1 物理模型 为研究不同孔隙形状与孔隙排布对冻结过程的影响，本文设置了四种不同的孔隙结构。图4为孔道的部分放大图。水侧位于孔隙骨架外侧，其中d为直径或边长，l为孔间距。

图4 四种孔隙结构尺寸图Fig.4 Dimension diagram of four pore structures

模型的几何尺寸与实验对象相同，边界条件设置及模拟取点位置如图5所示。下侧边界设置为恒定温度Th，提供冻结过程的冷量。根据上述的假设条件，上侧边界为绝热条件，两侧边界为对称条件。多孔介质边界为润湿壁条件。流体初始温度为5℃，流动状态为静止。图中标记点位置为后续实验和模拟所选测点。

图5 孔隙结构物理模型边界条件Fig.5 Boundary conditions of physical model of pore structure

1.3.2 数学模型 在平面坐标系中，该模型的控制方程为：

二维连续性方程

流体物性来自REFPROP 软件的材料库，各物性随温度的变化而变化。部分参数如表2所示。

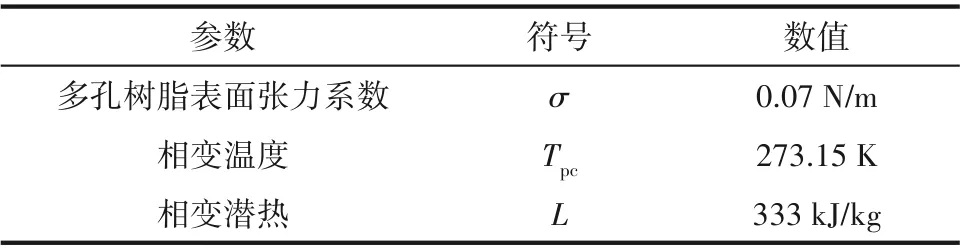
表2 模型物性参数Table 2 Physical parameters of model

1.3.3 模型验证 本文使用的模拟软件为Comsol。为验证模拟结果的准确性，将模拟结果与实验测试结果进行了对比。模拟条件如下：初始温度20℃，边界温度-20℃。模拟结果与实验结果对比如图6所示。

由图6 可知，模拟结果与实验结果有较好的吻合性，绝对误差平均值为1.4℃。实验值与模拟值的主要偏差集中在冻结初始阶段，原因是在实验过程中低温恒温槽输出的低温冷冻液到达冷板时会发生能量损耗，实际边界温度略低于-20℃，因此导致在冻结初始阶段降温速率与理论模拟有一定的差别。

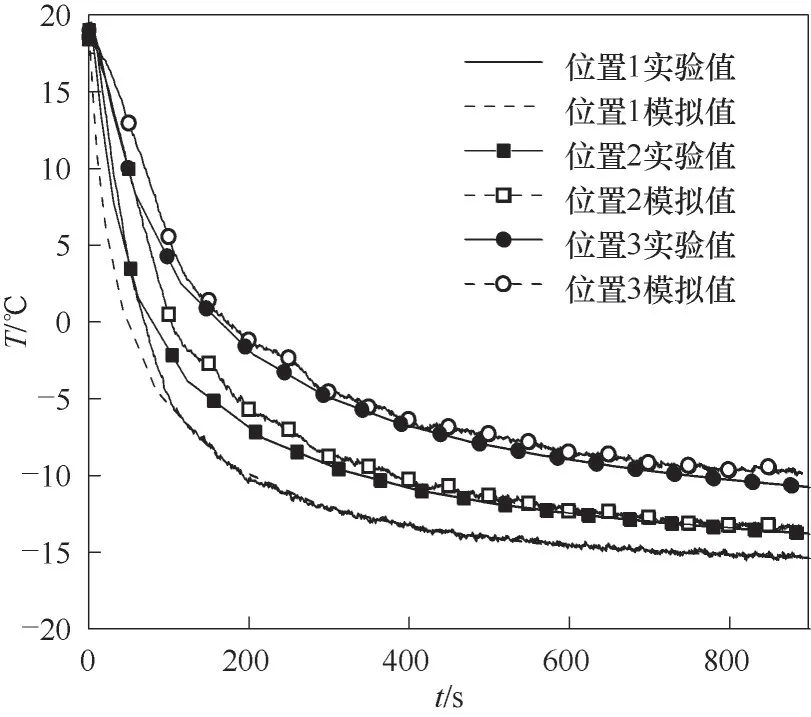
图6 冻结过程中相同位置温度模拟结果与实验结果对比Fig.6 Comparison of temperature simulation results and experimental results at the same position during freezing

2 结果与讨论

2.1 单向冻结实验结果分析

2.1.1 冻结面演变规律 根据毛细冻胀理论，接触角不同与微孔道结构变化会使相变过程受到不同程度的毛细作用力。根据Young-Laplace 方程理论计算，可以得到冻结面在经过孔道时，毛细压力的变化。图7（a）为孔道中孔隙半径分布示意图；图7（b）展示了在多孔树脂的孔隙结构中，随着冻结面推进，孔隙半径rp与最大毛细压力Pmax在相对位置h上的变化。相对位置h位于孔隙中轴线处。可以看出，圆形孔道中，毛细压力在孔隙半径最小处达到毛细压力最大值，之后随着孔隙半径增大而减小。

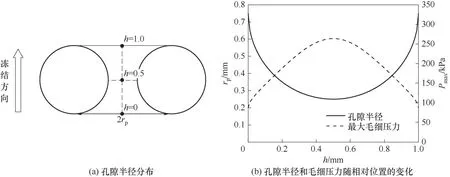
图7 微孔道中孔隙半径和毛细压力随相对位置的变化Fig.7 Variation of pore radius and capillary pressure with relative position in microporous channel

圆形微孔道中冻结面的相对曲率分析如图8(a)所示。在冻结面与壁的接触点处，冻结面受到冰壁表面张力和壁表面张力的影响，形成弯曲相界面现象，其中水与壁面的接触角为θlw。如图8(b)所示，在冻结初期，冻结面进入孔隙半径逐渐减少的孔道时，毛细压力Pc逐渐变大，边界毛细作用逐渐明显。在冻结面上共同受到水压Pw与冰压Pi的影响，由于毛细压力随冻结面在孔道中发展而变化，因此水压与冰压差也随之变化，如图8(c)、(d)所示。

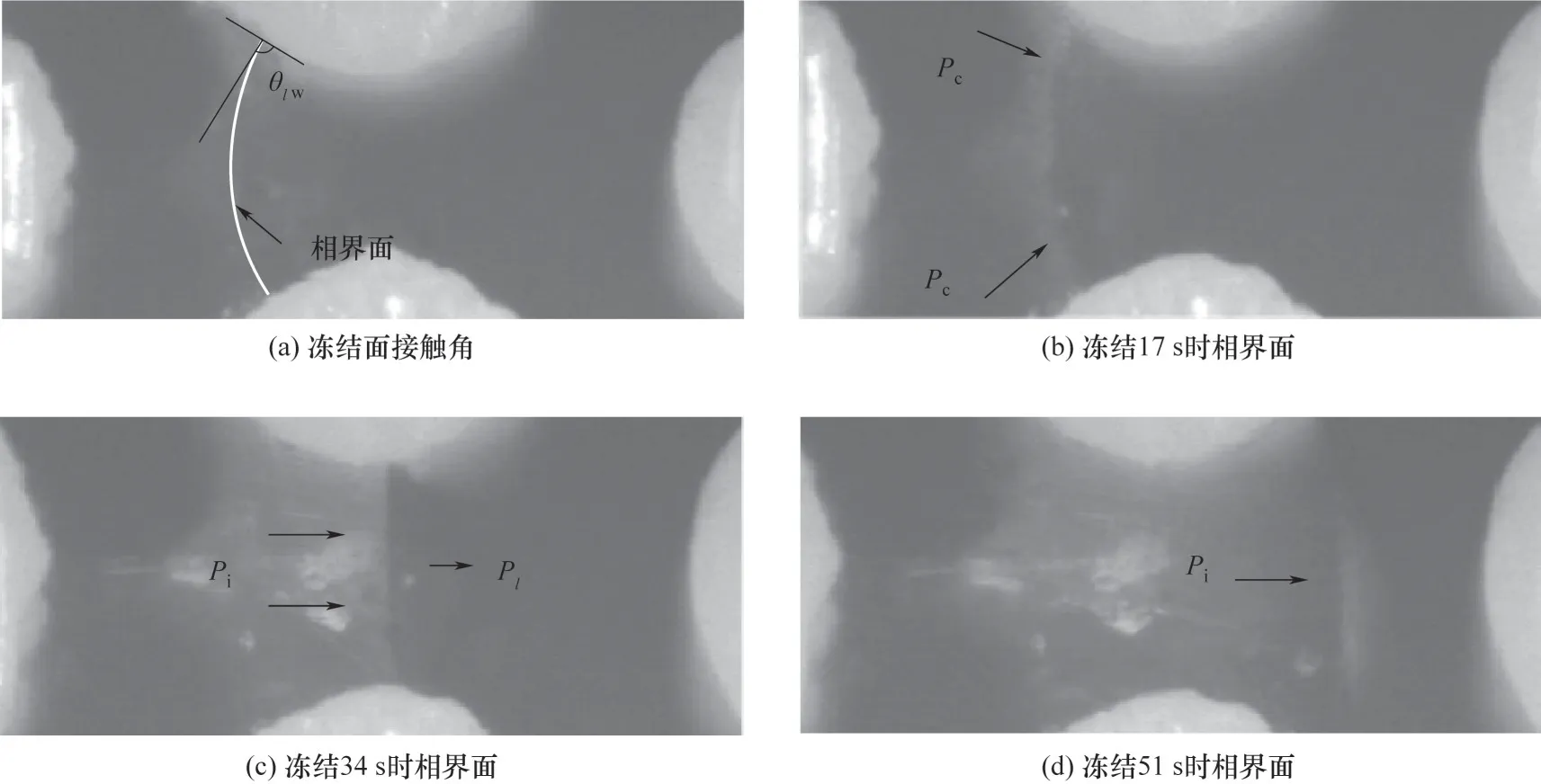
图8 冻结面变化示意图Fig.8 Schematic of frozen surface change

为量化界面曲率的变化，引入相对曲率概念研究相界面经过孔道时的变化。首先在相界面提取一定量的数据点，根据足够的数据点进行函数拟合，函数根据图9(a)中的坐标轴定义，之后把拟合出的函数代入式（14），得到相界面的相对曲率k。

如图9(b)所示为冻结面相对曲率随时间的变化。实线为根据实验中拍摄的冻结面所计算的曲率值，虚线为数值计算模拟值。可以看到，在冻结面经过一个圆形孔道时，相对曲率呈先上升后下降再上升最后下降的趋势。相界面从孔道发展结束，准备进入下一排孔道时，由于缺少孔壁约束，相界面逐渐平缓，相对曲率逐渐减小。进入孔道以后，毛细作用逐渐明显，表面张力从水、冰、壁面接触点向孔道中轴处影响，导致相对曲率逐渐增加。由于圆形孔道孔隙半径减小，导致毛细压力逐渐变大，冰压与水压差变大，冻结面会有突起的趋势（相对于冰侧），所以冻结面会从凹形向凸形发展，冻结面相对曲率会先下降至0（点b，平直界面）再上升至点c。最后，随着冻结面继续前移，孔隙半径逐渐变大，冻结面失去孔道的限制逐渐平缓，相对曲率逐渐下降。

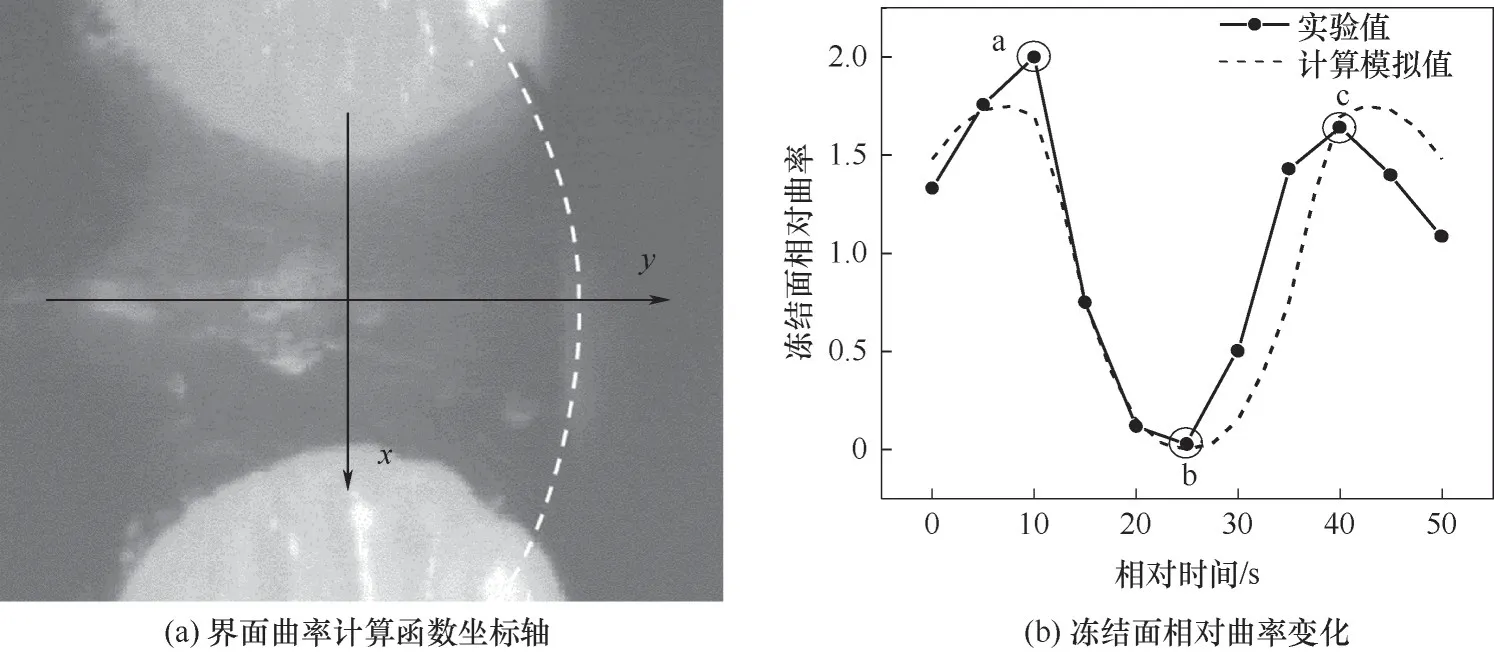
图9 冻结面相对曲率变化规律Fig.9 Change law of relative curvature of freezing surface

2.1.2 温度场演变规律 图10 显示了在边界温度Tc为-20℃的情况下，随着时间的变化，温度场在孔道间的演变，其中白色部分为多孔树脂固体骨架，彩色部分为孔道介质温度。在50 s 时，温度场沿着孔道向前推移至第三排孔道，至90 s 孔道温度到达7℃左右，在190 s 到达2℃左右， 在240 s 时，孔道温度到达0℃，到达310 s时，孔道温度达到-6℃。温度场下降速率呈先快后慢的趋势，与温度场发展的温度梯度有关。

图10 冻结过程中微孔道温度变化Fig.10 Temperature change of microporous channel during freezing

从图11 微孔道内测点温度随时间变化也可以得到相同结论。从图中可以看出，环境温度变化在1℃范围内，说明保温箱内温度基本不变，可视为实验在环境温度不变的条件下进行。孔道内温度受到温度梯度的影响呈先迅速下降、后缓慢下降的趋势，分界点在150 s 左右。位置1 的温度下降不但比位置3 快，300 s 时温度同样更低，说明微孔道内在300 s已经形成基本稳定的温度场，温度变化逐渐减小。所以如果要保持温度下降速度，需要改变边界温度，保证温度场形成一定的温度梯度。

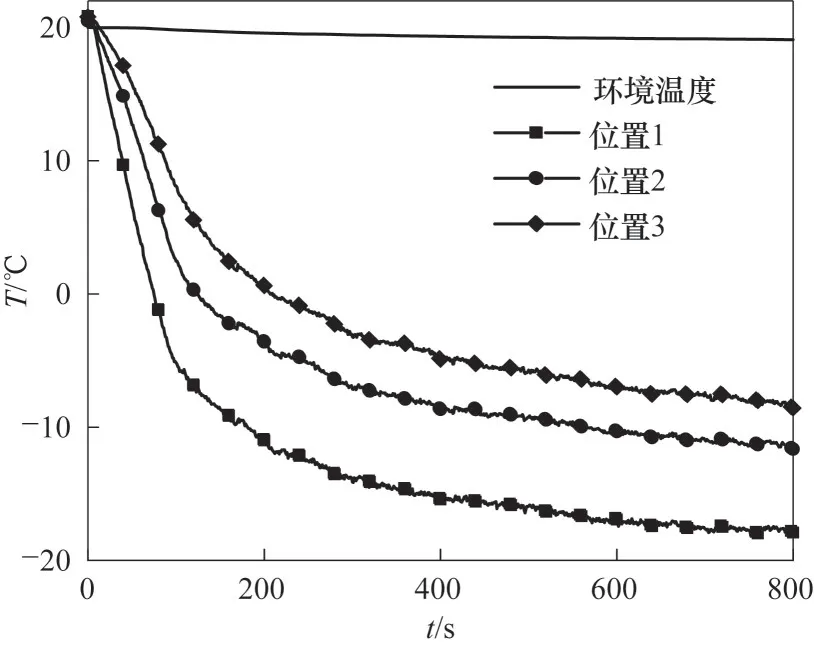
图11 单向冻结实验测点温度随时间的变化Fig.11 Temperature variation of measuring points with time in unidirectional freezing experiment

图10(d)中，相界面与0℃等温线有一定的距离，这是因为在多孔介质中，毛细压力会造成过冷的现象，因此在到达相变温度时并不会立即冻结，导致在0℃等温线与相界面之间出现过冷带。

为研究过冷带在孔道间的迁移，同时分析过冷带所处的温度场。图12为单个孔道中的温度演变，其中红色代表高温，蓝色代表低温，黄色代表温度范围为-1～0℃。选取时间为228、240、253、266 与285 s（相对时间为0、12、25、38、57 s）。可以从图中看出，由于交错排布的孔道结构，导致冷量从孔道两侧向中间汇聚，过冷带的形状呈月牙状。在进入孔道后，由于孔隙半径的减小，导致温度梯度在孔隙间迅速增大，因此过冷带在孔隙间曲率逐渐变小，并在253 s时可以清晰看到过冷带边界平直。然后随着温度场发展，过冷带进入下一排孔道。

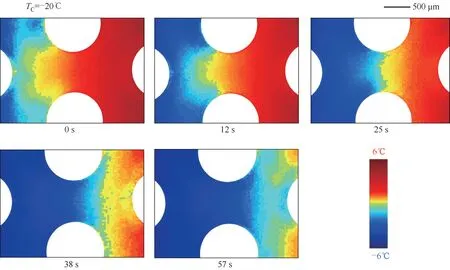
图12 单向冻结实验单孔道温度场演变Fig.12 Evolution of temperature field in single channel of unidirectional freezing experiment

2.2 单向冻结模拟结果分析

2.2.1 边界温度对温度场及冻结速率的影响 通过模拟可以得到边界温度为-15℃的温度场及对应的相界面云图，图13 所示为300 s 时的温度场及相界面云图。可以看出，300 s 时温度场发展至第六排，且前排温度梯度比后排高。相界面发展至第四排。

图13 在300 s时刻的温度场及相界面云图（边界温度-15℃）Fig.13 The temperature field and the phase interface cloud Contour at 300 s (boundary temperature -15℃)

为分析不同边界温度对温度场演变的影响，取一测试点（图5）进行研究，图14 展示了该点在不同边界温度时的冻结过程中温度变化曲线。从图中可以看出，在前200 s，由于温度梯度大，温度迅速下降并接近冻结温度，在200 s后，温度梯度趋于平缓，温度变化速率逐渐减小。边界温度越低，温度下降越快，不同边界温度主要影响发生在冻结开始阶段的温降速度与冻结晚期的稳定温度。不同边界温度条件下，该位置到达相变温度所用的时间也不同。边界温度为-5℃的条件下，该点在52 s 时达到相变温度，边界温度为-10℃的条件下需要22 s，而边界温度为-15℃的条件下，只需要14 s。

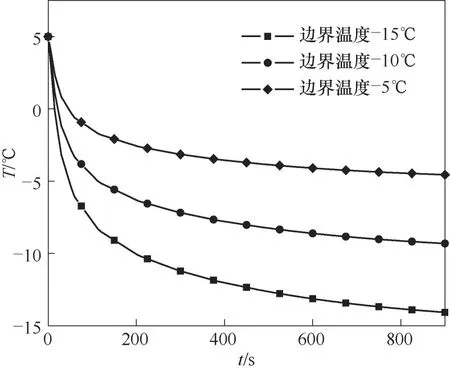
图14 不同边界温度在相同位置的温度变化Fig.14 Temperature change of different boundary temperatures at the same position

测试点处温度梯度随时间变化如图15 所示。可以看到在冻结至200 s左右，温度梯度发展至最大值，因此在0～200 s 的区间中，测点温度下降速率最快。而在200 s 之后，随着温度场向y方向的发展，温度梯度逐渐下降，因此在200 s后测点温度趋于稳定。同时边界温度为-5℃的最高温度梯度比边界温度-15℃的最高温度梯度小，说明温度越低的边界温度带来的温度梯度越高，发展至稳定的温度场所需的时间也越长。

图15 温度梯度随时间的变化Fig.15 Temperature gradient versus time

图16展示了不同边界温度下的平均冻结速率，边界温度为-10℃的冻结速率比边界温度为-5℃的冻结速率快36.37%，边界温度为-15℃的冻结速率比边界温度为-10℃的冻结速率快91%，证明边界温度可以显著提高冻结速率，并且边界温度越低冻结速率加快越明显。

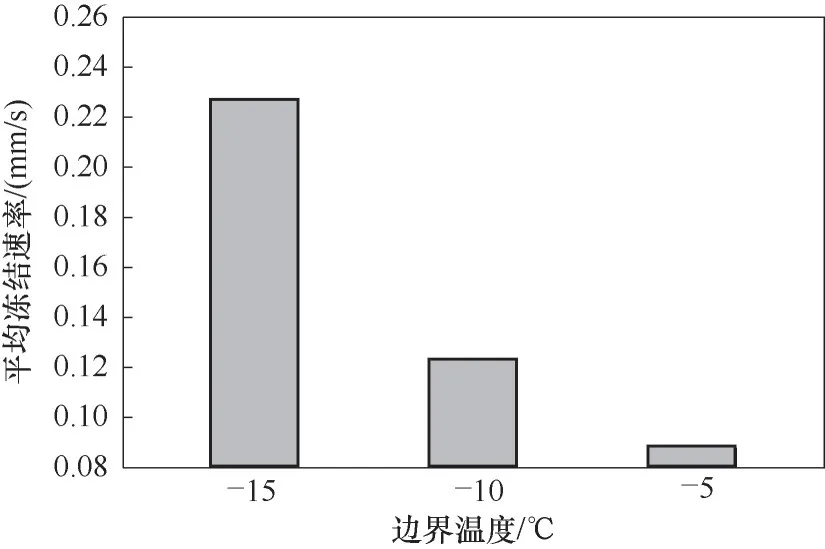
图16 不同边界温度下的平均冻结速率Fig.16 Histogram of average freezing rate at different boundary temperatures

2.2.2 孔隙间距对冻结速率的影响 为探究孔隙间距对温度场演变的影响机理，从温度梯度角度对边界温度为-15℃时，孔隙间距为500、200、100 和50 μm 的圆形交错孔隙结构进行分析。图17 为多孔介质中测点温度随时间的变化曲线。可以看到孔隙间距为500 μm的孔隙结构到达相变温度最快，需要14 s；孔隙间距为50 μm 的孔隙结构到达相变温度最慢，需要31 s。可以证明孔隙间距越小，温度变化速率越慢。

图17 不同孔隙间距中温度随时间的变化Fig.17 Temperature variation with time in different pore spacing

图18 显示了不同孔隙间距的孔隙结构中温度梯度随相对位置的变化。其中相对位置是指孔道中轴线位置，0 处位于孔道最窄处。可以明显看出，孔隙间距为500 μm 的温度梯度变化平稳，最高到1103 K/m，且变化范围更宽达到1.4 mm。孔隙间距为50 μm的温度梯度变化剧烈，最高达到1389 K/m，变化范围只在0.58 mm 内产生变化，可以量化证明温度梯度在孔隙中的变化。上述说明了不同孔隙间距对温度场发展产生影响的原因，由于在孔隙间距最小处发生温度梯度突跃，会阻碍温度场发展速度，并且突跃的程度与阻碍温度场呈正相关，因此孔隙间距越小，温度场发展越慢。

图18 单个孔道温度梯度随相对位置的变化Fig.18 Variation of temperature gradient of single channel with relative position

平均冻结速率如图19所示。由图可知，孔隙间距越小，平均冻结速率越慢。其原因是由于在该孔隙结构中，冻结过程主要由温度场驱动，温度场发展越快的孔隙结构，冻结发展速度也越快。结果表明，孔隙间距越小的孔隙结构，其冻结速率越慢。

图19 不同孔隙间距下的平均冻结速率Fig.19 Histogram of average freezing rate under different pore spacing

2.2.3 孔隙结构对冻结速率的影响 图20 为四种孔隙结构的平均冻结速率，可以看到冻结速率由快到慢分别是圆形直排、圆形交错、方形直排与方形交错。为进一步证明在多孔介质冻结过程中冻结场主要由温度场进行驱动演变，通过热流线及等温线研究四种孔隙结构对温度场演变影响的机理。图21为四种孔隙结构的多孔介质在同一时间、位置的温度场孔道局部图，其中红色代表高温，蓝色代表低温，黑线表示热流线及等温线，相邻两条等温线相差0.25 K。

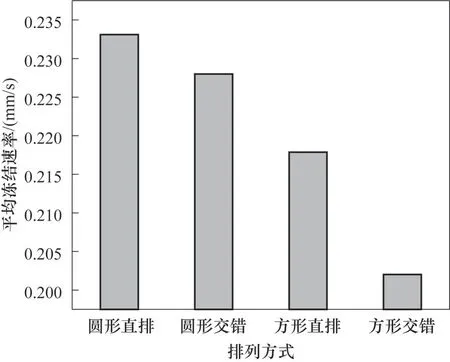
图20 不同孔隙结构下的平均冻结速率Fig.20 Histogram of average freezing rate under different pore structures

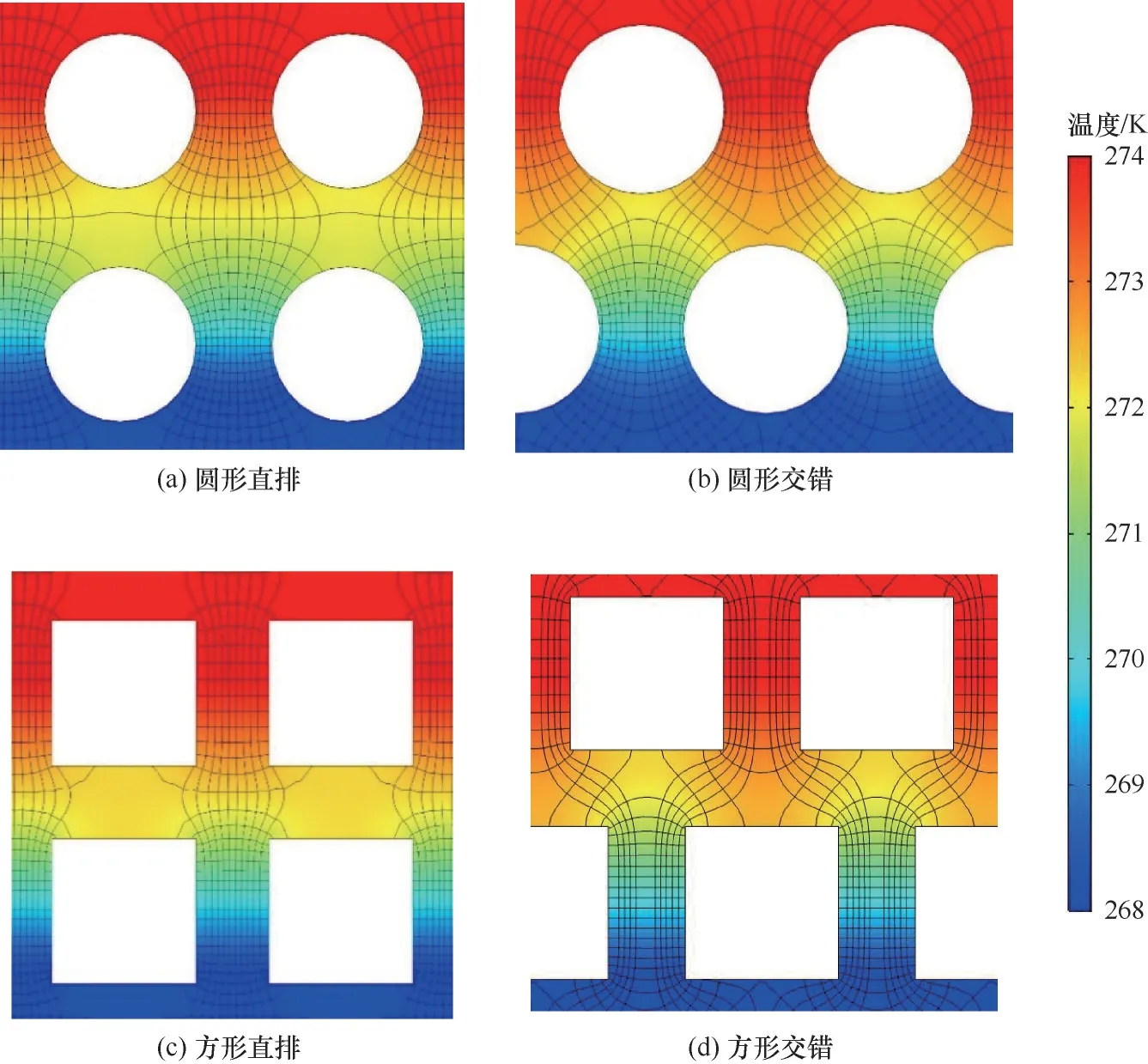
图21 不同孔隙结构温度场孔道局部图Fig.21 Partial diagram of pore channel for temperature field of different pore structures

通过对比圆形孔道与方形孔道，可以发现方形孔道由于受到形状的限制，当圆形孔道等温线已经进入孔道时，方形孔道等温线仍在孔道外的壁面上，因此，圆形孔道比方形孔道更利于传热。对比图中直排与交错排列的孔隙排布，交错孔道的热流通道（整体热流线）弯曲导致等温线的弯曲，这意味着一部分冷量提前向后部进行传热，导致传热面积的减小，减缓了冻结面进入孔道的时间，因此，直排孔道中温度场演变速率比交错孔道的温度场演变速率更快。结果表明，孔隙骨架形状越光滑，热流通道越趋于平直，温度演变越快。

3 结 论

本文实验研究了多孔介质单向冻结过程中相界面与温度场的演变，并通过数值模拟方法，研究了不同边界温度、孔隙间距及孔隙结构对多孔介质冻结过程及冻结速率的影响，得出如下主要结论。

（1）冻结面在经过孔道时，孔隙半径先减小后变大，毛细压力随之先增大后减小，因此相对曲率先减小后增大。冻结面从凹形向凸形变化，在孔道中轴处相对曲率下降至0，冻结面平缓。

（2）边界温度相同时，孔道内同一位置处的温度梯度先快速增加，随着冻结的进行逐渐减小，导致该点温度下降呈现先快后慢的趋势，最后趋于稳定。边界温度越低，形成的温度梯度越高，进而提高其冻结速率。不同边界温度，相同位置处，达到最高温度梯度的时间相同。孔道内水结冰过程存在过冷现象，0℃等温线和相界面之间存在过冷带。

（3）温度梯度在孔道最窄处会发生突跃，阻碍温度场的发展，孔隙间距越小，突跃越剧烈，冻结速率越低。孔隙结构对冻结速率的影响与孔隙骨架形状和排布方式相关，孔隙骨架的形状越光滑，冻结面进入孔道越快，排布方式越规律，温度演变越快。