自转式内置转子颗粒污垢抑制特性研究

谢广烁，张斯亮，王家瑞，肖娟，王斯民

（1 西安交通大学化学工程与技术学院，陕西 西安 710049； 2 上海蓝滨石化设备有限责任公司，上海 201518）

引 言

传热管是换热器内用于交换壳程流体和管程流体热量的元件，在能源化工领域的应用十分广泛。由于传热管的工作环境复杂多变，表面不可避免地出现许多污垢，其形成的原因主要有：颗粒沉积、结晶析出、化学反应、腐蚀、凝固相变、微生物繁殖和多种因素混合作用[1-2]。Steinhagen 等[3]调查了新西兰200 家公司的近2000 台换热器，其中90%以上的换热器都存在某种污垢问题，新西兰每年因污垢问题损失3000万～4600万美元。颗粒污垢的沉积不仅会增加析晶结垢的成核数量，还会为生物的聚集、生长、繁殖提供场所，使多种污垢并存、难以去除[4-5]。因此，对传热管内颗粒污垢生长和抑制特性的研究具有重要意义。

研究者分别采用不同的数值模型，研究了气固两相流中微细颗粒在壁面上的沉积特性，并考察了颗粒粒径、入口速度、表面材料等因素对颗粒沉积的影响[6-10]。张宁等[11]采用离散相模型结合经验公式的方法模拟了二氧化硅颗粒在换热面上的沉积和剥蚀过程，研究了不同因素对管壁污垢热阻的影响，发现增大流速和入口温度，减小管壁粗糙度有利于减小颗粒污垢热阻。Kasper 等[12]提出一种基于拉格朗日粒子跟踪和欧拉方法的多相耦合模型，采用大涡模拟得到通道内的流体流动，对比了方腔表面和球形窝表面的颗粒沉积，揭示了球形窝内不对称涡结构的存在。Tang等[13]采用离散相模型和动网格对管束式换热器中粉煤灰的沉积和去除过程进行数值研究，建立了颗粒结垢的判断准则，预测了污垢形态对传热性能的影响，显示颗粒越小，结垢率越高。Seyyedbagheri 等[14]采用欧拉方法研究了管道中沥青质沉积过程，考虑了涡旋扩散、湍流泳动、热泳动、重力和分子扩散等沉积机制，发现沥青质沉积速率随油流速度的增加而增加，而通过增加管道表面粗糙度来增加沥青质沉积速率仅在粒径小于20 μm 时有效。Vasquez 等[15]使用双流体欧拉方法研究了90°弯管中粗颗粒的传输和沉积，模拟结果与实验数据吻合较好，表明双流体方法在预测粗颗粒输运和壁面沉积方面具有替代典型拉格朗日方法的潜力。Ni 等[16-17]通过扩展欧拉模型并考虑布朗扩散、湍流扩散、湍流泳动和热泳动作为运输机制，预测了中间包中浸入式喷嘴内的夹杂物沉积速率，结果表明流动的不均匀造成了浸入式喷嘴内壁面上不同位置夹杂物沉积速率分布不均，同时湍流泳动导致大尺寸夹杂物的沉积速率更大。因此，数值计算已成为目前研究颗粒沉积的重要方法。

管内插件技术作为被动强化传热技术被广泛应用在热交换器中，在管内插入转子能够增强传热效率，达到在线防垢除垢的效果。张琳等[18-19]研究了自转式螺旋扭带管内的流动和湍流特性，提出了旋转扭带强化传热的四种机理，并分析了不同扭率下传热强化的主要控制机理。Zhang 等[20]通过实验研究了自旋扭带换热管的传热特性，对比了自旋扭带和固定扭带在湍流状态下的热特性，结果表明随着自旋扭带扭转比降低，Nusselt 数、压降和热性能因子均增加；自旋扭带能够更好地提高换热器的传热性能。Arasteh 等[21]通过数值模拟研究了管内插入固定或旋转扭带的传热强化效果，结果表明，在较低Reynolds数时旋转扭带拥有比静止扭带更好的传热强化性能。姜鹏等[22]建立了内置转子圆管内CaCO3污垢形成的数学模型，得到了圆管内污垢沉积率、剥蚀率和净存速率随时间的变化情况，发现光管内污垢热阻稳定值约为内置转子圆管的3～4倍。张震等[23]采用Mixture 模型对比了光管和内置螺旋叶片转子强化管的抑垢性能，结果表明强化管的抑垢性能比光管好，颗粒直径对传热管内颗粒污垢体积分数的分布具有明显影响。刘鑫[24]采用Mixture 模型研究了间距和偏心距对组合转子抑垢性能的影响，获得颗粒污垢在传热管轴向上的变化曲线，发现无间距排列和偏心距为2 mm时组合转子的抑垢性能最好。以上文献表明自转式内置转子可在无外加动力的情况下除垢抑垢，但未针对自转式内置转子不同转速下圆管内颗粒污垢特性展开研究。

本文提出一种新型自转式内置转子，采用欧拉-欧拉多相流模型，通过UDF 加载颗粒污垢沉积和剥蚀数学模型，建立内置转子传热管内的颗粒污垢数值仿真计算模型，研究内置转子对传热管内流动传热性能的影响，分析不同流速下颗粒污垢特性，并对比转子固定和转动两种形式下的抑垢效果。

1 数值计算方法与几何模型

1.1 几何模型

如图1 所示，建立了内径28 mm，长300 mm 的传热管。在传热管中心处插入一个转子，由一个六边形面扭转90°得到，在径向最大处两端各倒出一个半径10 mm 的圆角，以防止转子棱角刮蹭管壁。转子直径26 mm，节距78 mm，左右两端各装有一个直径5 mm、高10 mm 的圆台，以便转子在实际应用中与连接件的安装。

图1 几何模型Fig.1 Geometric model

1.2 数学模型

采用欧拉-欧拉模型对传热管内的液固两相流动进行模拟，运用UDF 结合经验公式，考虑扩散沉积、湍流泳沉积、热泳沉积和重力沉积建立颗粒的沉积模型。颗粒污垢的形成是颗粒沉积与颗粒剥蚀共同作用的结果，引入颗粒剥蚀模型和污垢热阻模型，最终建立起传热管内颗粒污垢的数学模型。

1.2.1 控制方程 欧拉-欧拉模型将固体颗粒和液体视为相互渗透的连续介质，都在欧拉坐标系下求解，考虑液体相与颗粒相速度滑移与温度滑移的基础上，区分了颗粒扩展与滑移作用。欧拉-欧拉模型的控制方程如下：

由于转子的结构对流体具有扰流和引导作用，管内主流存在强烈的旋转，同时流动过程还存在二次流和剪切应力梯度剧烈变化的区域，即表现出对流线弯曲的敏感性及高度的各向异性，因此湍流模型采用RNGk-ε模型，提高计算旋流的精度和可信度。其中湍动能k及其耗散率ε由以下输运方程得到：

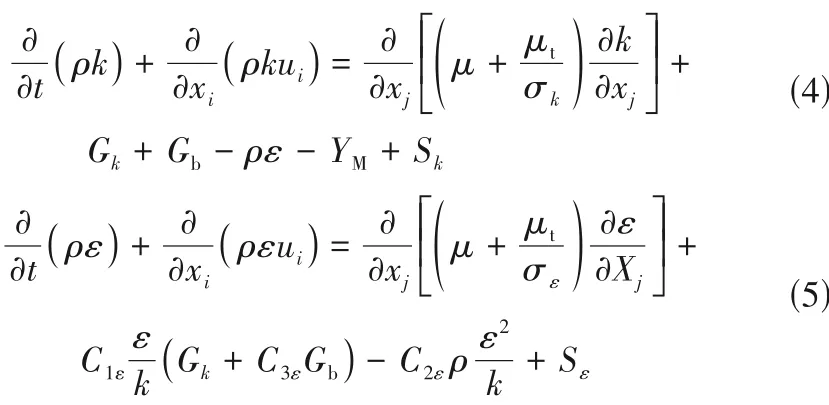
1.2.2 颗粒沉积模型 Wood[25]提出了管道流动中气侧颗粒沉积的经验公式，通过类比的方法，考虑水中微米颗粒沉积的四种有效沉积机制[26]：扩散沉积、湍流泳沉积、热泳沉积和重力沉积，其无量纲沉积速率的形式为：

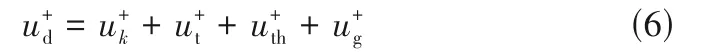
Shaw 等[27]通过实验研究提出了扩散引起的无量纲沉积速率方程：

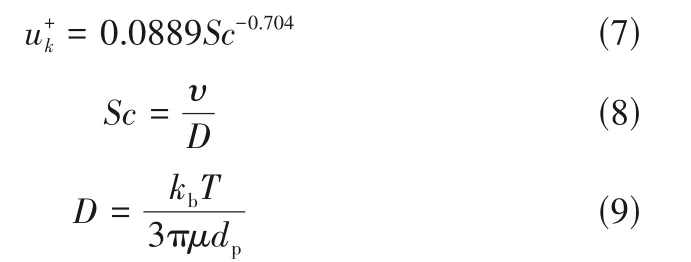
Wood[25]提出的沉积速率中包含了湍流泳沉积项，将该项中的空气运动黏度转化为水的运动黏度，即可得到微米颗粒在水中的湍流泳沉积公式：

Mcnab 等[28]通过实验研究提出了液侧微米颗粒的热泳沉积公式：

本文中氧化镁颗粒的直径为20 μm，重力对颗粒沉积的影响不可忽略，无量纲重力沉积速率公式为[29]：

沉积率ṁd受到沉积速率和颗粒质量浓度的影响，沉积率计算公式为[30]：

将以上公式编写为程序语言，编译后的程序与欧拉-欧拉模型结合便可求出传热管内的颗粒沉积率。

1.2.3 颗粒剥蚀模型 颗粒污垢热阻的形成包括颗粒在壁面上的不断沉积和剥蚀两个过程，颗粒的剥蚀与壁面剪切力和污垢黏结强度因子有关，Nae-Hyun 等[31]研究了管内液侧颗粒污垢的形成过程，并提出颗粒的剥蚀率计算公式：

1.2.4 污垢热阻模型 颗粒污垢特性是沉积和剥蚀过程的动态平衡，当颗粒剥蚀率逐渐增加至与颗粒沉积率相等时，颗粒的污垢特性趋于稳定，这时颗粒污垢热阻也达到稳定。假定污垢的成分和特性沿换热面和垢层厚度方向是均匀分布的，则污垢热阻为：

1.3 边界条件

采用瞬态计算，沿y轴负方向设置重力加速度，大小为9.81 m/s2。流体连续相为水，分散相为直径20 μm 的氧化镁颗粒，转子材质为铝，管壁材质为钢，计算物性参数如表1 所示。采用速度入口和压力出口边界条件，介质入口温度为30℃，管壁为恒壁温50℃，通过多重参考系法模拟转子的转动，设置转子所在流体区域为旋转区域。求解策略基于有限体积法，压力-速度耦合方式采用SIMPLE 算法，动量方程、能量方程、湍动能及其耗散率方程均采用二阶迎风格式。瞬态时间步长设置为0.005 s，各项残差小于10-3时认为计算收敛。

表1 介质物性参数Table 1 Physical parameters of the medium

自转式内置转子的工作原理是在管内依靠流体的推动获得动力矩，从而产生旋转。本文通过可视化冷态实验，采用光电测速仪测量不同流量下内置转子稳定旋转时的转速，最终得到文中模拟流速下对应的转子转速。实验流程和实验装置布置分别如图2 和图3 所示，实验过程中通过改变泵频率和回路阀门开度调节流量，控制体积流量从66 L/min 逐渐减小到8 L/min，每2 L/min 作为一个工况点。实验结果表明，随着体积流量的增加，转子转速逐渐增加，呈明显的线性变化，通过线性回归，得到转速随不同入口流速的拟合曲线。因此，本文流体入口流速为0.15、0.20、0.25、0.30、0.35 m/s，对应转速分别为28、48、69、89、109 r/min。

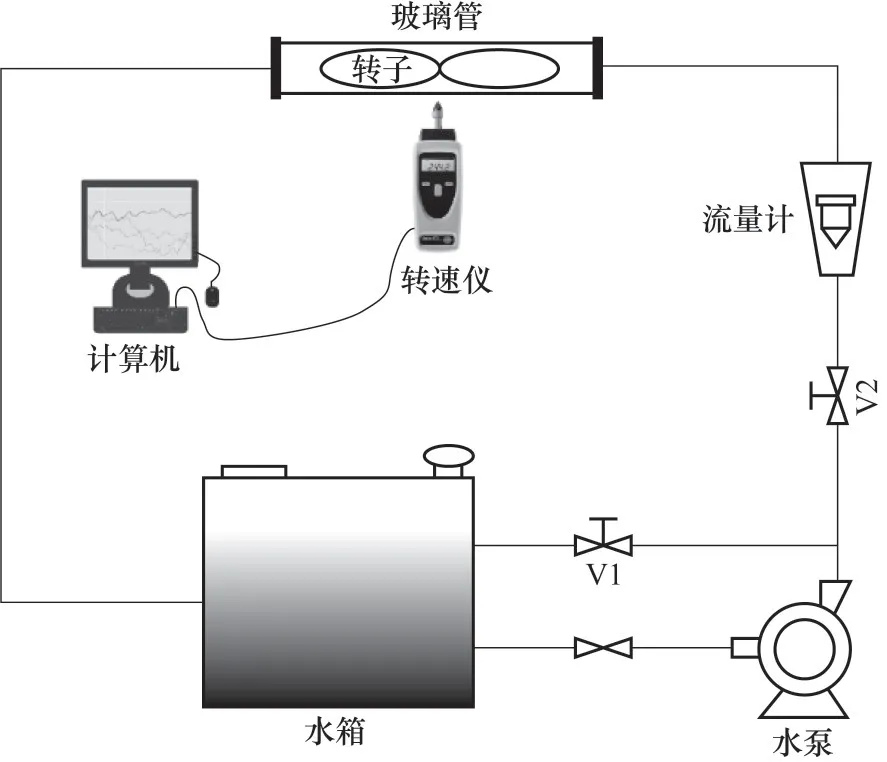
图2 实验流程示意图Fig.2 Schematic diagram of experimental process

图3 实验装置布置图Fig.3 Arrangement diagram of experimental setup

2 网格无关性验证与模型验证

将整个流体区域划分为转子附近的旋转区域和剩余的相对静止区域，分别设置网格尺寸，并对转子表面进行加密。通过改变网格尺寸大小来调整网格数量，并进行网格无关性测试，结果列于表2。当网格数量增加到4923102个时，传热管内稳定沉积率变为1.69×10-4kg/(m2·s)，相比于网格数量为3203782 个时变化了3.4%，该值小于5%。综合考虑计算准确度和计算时间，本文采用网格数为4923102个的网格。

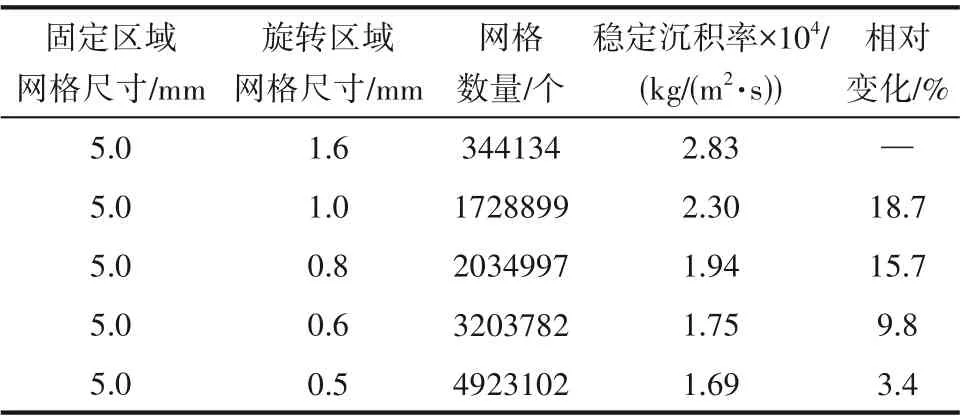
表2 网格无关性测试Table 2 Grid independence verification

本文通过复现文献[32]中内置扭带换热管的流动传热结果以验证采用MRF 模型和RNGk-ε模型对内置转子传热管内流场和温度场计算的准确性。表3 展示了模拟值与文献中数据的对比情况，从表中可以看出，在各种工况下压降的相对偏差均在3.5%以内，平均表面传热系数的相对偏差均在9.0%以内，说明了内置转子传热管内流场和温度场的计算具有较高的准确性。

表3 内置扭带换热管流场温度场对比验证Table 3 Model verification of flow and temperature fields with build-in twisted tape

采用文献[33]中不同入口速度下圆管内颗粒污垢热阻变化情况进行颗粒污垢数学模型验证。从图4中可以看出，计算结果与文献中的实验数据变化趋势一致，污垢热阻都是先增加，一段时间后达到一个渐近值，且随着流速的增加污垢热阻渐近值逐渐减小。三种流速下污垢热阻渐近值的相对偏差均在12.0%以内，平均偏差为8.4%，在两相流计算误差可接受范围内。因此，本文所采用的欧拉-欧拉模型和颗粒污垢模型是准确可靠的。

图4 污垢热阻模拟值与实验数据的对比曲线Fig.4 Comparison curves of fouling resistance between simulated values and experimental data

3 结果与讨论

3.1 内置转子对传热管内流场的影响

本节在流体流速为0.25 m/s 的情况下，分析了自转式内置转子对传热管内速度场和温度场的影响，并对比了传热管内无转子和转子固定不动时的流场，为进一步分析传热管内颗粒污垢特性提供依据。

图5 为三种形式下传热管z=0 截面上速度分布云图。从图中可以看出，在无转子的传热管内流体流动速度变化不大；转子固定时，由于流体直接冲刷转子，在转子最大径向截面尾流区出现局部速度增大，约为0.31 m/s；转子转动时，流体流经转子最大径向截面前后速度较为均匀，流经转子后，传热管轴线上的流体速度略小于传热管两侧的流体速度。流体流经转子过程中，传热管壁面边界层减薄，这是因为转子的扰流作用使流体的径向速度和周向速度增加，增加了流体的紊流程度。

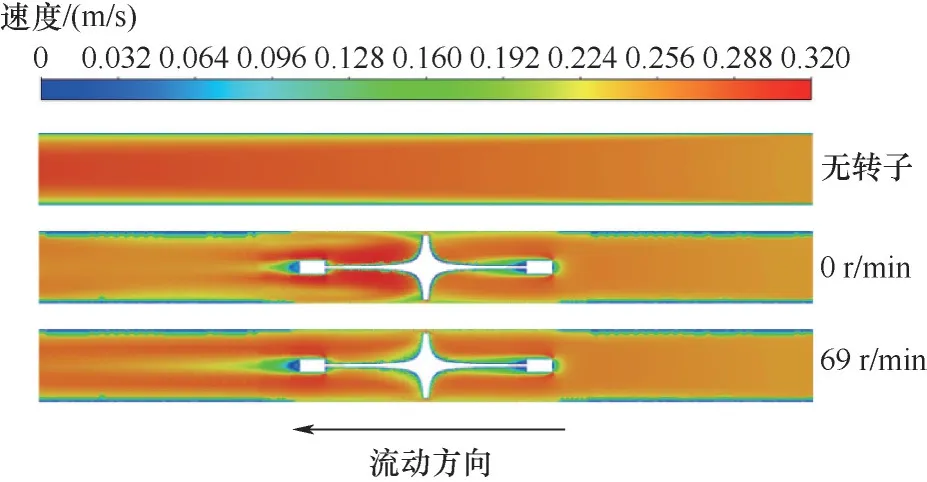
图5 传热管z=0截面上速度分布云图Fig.5 Velocity contour on z=0 section of heat transfer tube

图6为三种形式下传热管内流体流线图。从图中可以看出，在无转子的形式下，流体主要沿着轴向流动，流体扰动并不强烈；在转子存在时，流体流经转子的过程中受到转子的引流作用，流体由原来的轴流流动变为螺旋流动，流体的紊流程度大大增加，这不仅有利于传热管内的流动换热还增强了流体对管壁污垢的冲击剥蚀作用。在转子固定不动形式下，流体流经转子前半部分时，转子对流体的引流作用并不强烈，流体仍以轴流为主；随着流体与转子的接触增加，转子对流体的引流作用逐渐增强，流体的螺旋流动逐渐强烈，且在流体流经转子后仍有较强的螺旋流动。在转子转动时，旋转区域附近均出现了较强烈的螺旋流动，而由于自转转子对流体的引导作用相对固定转子较弱，流体流经转子后的螺旋流动迅速减弱，并逐渐恢复轴向流动。

图6 传热管内流线图Fig.6 Pathlines of heat transfer tube

图7 为三种形式下传热管z=0 截面上温度分布云图。由图可知，流体平均温度随着流程逐渐增加，转子存在时流体温度增速更快，三种形式下流体的温升分别为1.02、1.05、1.03℃。传热管轴心处流体温度较低，沿着径向方向流体温度逐渐增加，流体受到转子扰流作用，温度梯度减小。转子固定不动时，流体的扰流效果较强，使得轴心处温度明显高于其他两种形式；同时流体经转子引导后会冲击管壁，在冲击位置流体与管壁的换热量大幅提升。转子转动时，流体对壁面的碰撞增强，使得旋转区域内靠近管壁流体温度提升明显。

图7 传热管z=0截面上温度分布云图Fig.7 Temperature contour on z=0 section of heat transfer tube

图8 为三种形式下传热管z=0 截面上压力分布云图。从图中可以看出，转子存在时流体的压降显著增加，且转子转动时管内压降比转子固定时小，三种形式下流体的压降分别为12.82、21.87、17.70 Pa。转子固定时，转子前部对流体的阻挡作用较强，流体在转子阻挡位置出现压力激增，在靠近转子后半部分的位置出现负压。转子自转时，转子随流体的冲击而转动，因而对流体的阻挡作用相对较弱，只在圆台前部出现压力激增，阻力损失相比固定形式更小。

图8 传热管z=0截面上压力分布云图Fig.8 Pressure contour on z=0 section of heat transfer tube

3.2 内置转子传热管内颗粒污垢动态特性

由于颗粒污垢特性是颗粒沉积和剥蚀动态平衡的过程，本节对不同流速下自转式内置转子传热管内颗粒沉积率、颗粒剥蚀率以及颗粒污垢热阻的动态变化进行了分析。

图9为不同流速下传热管内颗粒沉积率的变化情况。从图中可以看出，在1.0 s 内五种流速下的沉积率都达到了稳定值。随着流速的增加，污垢稳定沉积率呈递增趋势，而且流速越大污垢稳定沉积率增长越快。在流速为0.15 m/s 时，污垢沉积率为1.56×10-4kg/(m2·s)；流速为0.25 m/s 时，污垢沉积率为1.99×10-4kg/(m2·s)，较最低流速时增加了27.6%；当流速为0.35 m/s 时，污垢沉积率增加至3.69×10-4kg/(m2·s)，较最低流速时增加了136.5%。这是因为随着流速的增加，转子转速越快，流体流经转子时的螺旋流动越强烈，流体与传热管壁面的碰撞增加，单位时间内到达壁面的污垢颗粒数目增加，污垢沉积率随之增加。

图9 沉积率随时间的变化曲线Fig.9 The curve of deposition rate with time

图10 为不同流速下污垢剥蚀率随时间的变化情况。从图中可以看出，污垢剥蚀率随着时间逐渐增加，流速越大剥蚀率增长越快，且渐近值随着流速的增加而增加。随着流速的增加，流体流经转子时的周向速度和径向速度更大，流体对壁面上污垢的冲击增强，导致流体对污垢的剥落效果得到增强；同时，壁面剪切力随着流速的增加而增大，壁面剪切力越大，污垢越容易脱落，污垢剥蚀率增加。由于污垢剥蚀率与污垢净沉积有关，低流速下污垢沉积率低，污垢的净沉积增加缓慢，因此低流速下污垢剥蚀率增加缓慢。

图10 剥蚀率随时间的变化曲线Fig.10 The curve of removal rate with time

图11 为不同流速下传热管内污垢热阻随时间的变化情况。由图可知，随着流速的增加，污垢热阻渐近值呈减小的趋势。当流速为0.15 m/s 时，传热管内的污垢热阻渐近值为3.79×10-4m2·K/W；流速为0.35 m/s 时，污垢热阻渐近值减小为1.96×10-4m2·K/W，减少了48.3%。流速增加，在转子的作用下流体对壁面的冲击增大，使得壁面剪切力增大，颗粒污垢的剥落增加。虽然随着流速增加沉积率也会增大，但剥蚀率的增长幅度大于沉积率的增长幅度，因此速度越大污垢热阻渐近值越小。当流速大于0.25 m/s 时，随着流速的增加，污垢热阻渐近值不再发生明显变化，因为剥蚀率随流速变化的增长幅度不再明显大于沉积率。

图11 污垢热阻随时间的变化曲线Fig.11 The curve of fouling thermal resistance with time

另外，随着流速从0.15 m/s 增加到0.35 m/s，达到污垢热阻渐近值所需要的时间逐渐减少，由120 h减少到25 h。流速为0.15 m/s 时，沉积率和剥蚀率都相对较小，导致污垢热阻的净增速度较慢；且污垢热阻渐近值较大，因此该情况下达到污垢热阻渐近值的时间较长。这也解释了0.15 m/s 的污垢热阻在前20 h 小于0.35 m/s 的污垢热阻，在20 h 以后大于0.35 m/s的污垢热阻的现象。

3.3 内置转子抑垢性能对比

在自转式内置转子传热管内颗粒污垢动态分析的基础上，对比不同流速下固定转子传热管内颗粒稳定沉积率与污垢热阻渐近值，为实际应用中转子的设计和选择提供参考。

图12 为两种转子形式下稳定沉积率随流速的变化情况。从图中可以看出，随着流速增加稳定沉积率逐渐增加，转子固定不动时的沉积率一直大于转子转动时的沉积率，且流速越大两种形式下的沉积率相差越明显。转子固定不动时，流体的螺旋流动更加强烈，大量内部流体携带颗粒流向管壁，且颗粒与管壁的碰撞角度更大，这都更有利于颗粒在壁面上的沉积，造成了污垢沉积率在转子固定形式下更大的情况。随着流速的增加，固定式转子与自转式转子沉积率的差值从0.02×10-4kg/(m2·s)增加到1.82×10-4kg/(m2·s)，这是因为两种形式下的流动差别更加明显。转子转动时，流体可以顺利通过转子，流体的流动情况随流速变化较小，所以沉积率随流速的增幅较为平缓，增加了136.5%，而转子固定时增加了248.7%。

图12 不同流速下稳定沉积率变化曲线Fig.12 The curve of stable value of deposition rate under different flow velocity

图13 为两种转子形式下污垢热阻渐近值随流速的变化情况。从图中可以看出，在转子转动的形式下，随着流速的增加，污垢热阻渐近值逐渐减小；而在转子固定的形式下，随着流速的增加污垢热阻渐近值先减小后增加。在转子固定形式下，沉积率和剥蚀率都会随着流速的增加而增加，当沉积率增长幅度大于剥蚀率时，污垢热阻渐近值增加。在计算工况范围内，当流速小于0.25 m/s 时，转子固定形式下的污垢热阻更小，最大相差13.1%；流速大于0.30 m/s 时，情况相反，转子转动形式下的污垢热阻更小，最大相差17.1%。可见污垢热阻与转子形式和工况参数密切相关，随着流速的增加污垢热阻并不一定会减少，在不同流速下选择转子的形式也会发生变化。

图13 不同流速下污垢热阻渐近值变化曲线Fig.13 The curve of stationary fouling resistance under different flow velocity

4 结 论

本文利用欧拉-欧拉模型模拟了传热管内的液固两相流，并结合UDF 自定义程序构建了传热管内颗粒污垢沉积和剥蚀模型，研究了内置转子的传热强化作用和除垢抑垢功能，并对比了固定转子和自转转子在不同流速下的抑垢特性，主要结论如下。

（1）在转子的作用下，流体的流动由轴流流动变为螺旋流动，流体的周向速度和径向速度增加，增加了流体内部混合的同时也增强了流体对管壁的冲刷作用。因此，传热管内插入转子的方式既有利于传热管的流动换热又有利于传热管的除垢抑垢性能。

（2）对于自转式内置转子传热管，随着入口流速从0.15 m/s 增加到0.35 m/s，传热管内稳定沉积率和剥蚀率渐近值都逐渐增加，且增速越来越快；污垢热阻渐近值逐渐减小，且减少的速度越来越慢。由于转子的扰动使流体与管壁碰撞增强，单位时间内沉积到管壁的颗粒数目增加，同时壁面剪切力增强，污垢剥蚀量增加；当两者增加幅度相近时，污垢热阻渐近值的变化较小。

（3）自转式转子和固定转子两种形式下的抑垢性能随流速的变化而变化。在流速0.15～0.35 m/s范围内，转子固定形式下的稳定沉积率一直比转子转动时更大。随着流速的增加，转子固定形式下的污垢热阻渐近值先减小后增加，转子转动时的污垢热阻渐近值一直减小，当流速高于0.30 m/s 时转子转动时的污垢热阻渐近值较小。

符 号 说 明

c——颗粒浓度，kg/m3

D——扩散系数，m2/s

dp——颗粒粒径，μm

H——焓值，J

k, kp——分别为流体热导率和颗粒热导率，W/(m·K)

kb——Boltzmann常数，1.38×10-23J/K

mf——颗粒净沉积总量，kg/m2

p——压强，Pa

T——温度，K

t——时间，s

ud——沉积速率，m/s

u*——壁面剪切速度，m/s

α——体积分数

λf——污垢层热导率，W/(m·K)

μ——动力黏度，Pa·s

ξ——污垢黏结强度因子，N·s/m2

ρ——密度, kg/m3

τ——弛豫时间, s

τ+——无量纲弛豫时间

τw——剪切力，N/m2

υ——运动黏度，m2/s

下角标

d——沉积

f——污垢

i,j——矢量分量

k——状态相，k=l时代表流体相，k=p时代表颗粒相