印刷板式微通道换热器流动与传热特性的理论模型

余智强，吴建泽，任亚涛，何明键，于喜奎，齐宏

（1 哈尔滨工业大学能源科学与工程学院，黑龙江 哈尔滨 150001； 2 空天热物理工业和信息化部重点实验室，黑龙江 哈尔滨 150001； 3 中国航空工业集团公司沈阳飞机设计研究所，辽宁 沈阳 110035）

引 言

随着世界能源资源减少、能源成本增加和环境问题日益突出，节约能源成为可持续发展目标的关键之一。根据美国能源信息管理局（EIA）的数据，到2040 年时世界能源消耗将增加56%。无论是化石能源还是可再生能源，都需要更新、开发更加高效的能源技术与设备[1]。在创新应用中，高效、紧凑型印刷板式换热器（PCHE）在热管理系统整体效率中发挥着至关重要的作用[2]。

1981 年，Tuckerman 等[3]首先提出了微通道散热器的概念，并预测其能以1000 W/m2的速率散去热量。微通道是通过微变形、微铣削、激光加工、化学刻蚀等技术，在单层金属薄板上加工出的微小的流道[4]。由于流道加工过程与印刷电路板类似，此类换热器被称为“ 印刷板式微通道换热器”（PCHE）[4-5]。相比于传统换热器，PCHE 具有传热系数高、体积小、紧凑度高、质量轻等特点，在生物工程、微加工系统、微泵、微热管等领域有广泛应用[6]。在“微尺度效应”[7]的作用下，传统换热器特性的计算方法变得不再适用，很多研究者针对这一问题展开研究，建立相关的准则关联式来预测PCHE 的流动与传热特性。

在对微通道内流动特性的研究中，Muzychka等[8]对非圆管内流体力学特性进行了详细的分析，提出以横截面积的平方根作为特征尺寸比水力直径更合适，同时构建新的模型并简化了非圆管f-Re的预测，基于实验数据获得了很好的相关性。Hun[9]采用Heatric UK 制造的PCHE 开展实验研究，提出Fanning 摩擦系数和Nusselt 数与平均Reynolds 数-Re呈线性关系，指出Re的函数依赖于通道中尖角弯头处的形状损失；通过数值模拟和实验测试数据对Fanning 摩擦系数关联式进行修正，给出在不同角度、节距和水利直径下关联式的修正因子。Chen[10]通过实验研究了换热器两侧压损，提出压降主要由两部分产生：换热器核芯的压降，分配装置（如入口/出口和流量分配集管）的压降，在Hun[9]研究的基础上根据换热器内部动量变化、摩擦作用、突扩、突缩等因素的影响提出了PCHE 压力损失的计算模型，对比发现实验测量结果与模型之间差异是由于通道变化造成的，并且在层流区域压降强烈依赖于流道的几何形状和尺寸。Chen 等[11]采用以Sharifi 等[12]和Chen[10]为基准的动态模型，对缩小尺度的直流道PCHE 的稳态和瞬态行为进行了数值预测，通过实验验证了该动力学模型在He/He条件下预测直通道PCHE性能的适用性。Bahrami等[13]基于椭圆通道提出了一种新的近似解，用于测定任意截面单连通微通道中充分发展的层流单相流的压降，该模型通过矩形、梯形和三角形微通道的实验数据进行了验证，还与不同横截面形状（超椭圆、梯形、正弦、菱形、圆形扇形等）通道的数值结果进行了比较，预测压降误差在8%以内。

在对微通道内换热特性的研究中，Kim 等[14]采用光刻技术加工出两个不同结构的PCHE，以水作为冷、热介质研究不同Reynolds数下的换热特性，提出用修正的威尔逊图法计算热侧和冷侧传热系数的关联式，与实验结果相比呈现出了很好的精度，误差在7%以内。Park 等[15]采用离散化方法得到了沿PCHE 径向的局部Nusselt 数，并采用不同的数据简化方法与PCHE 实验结果进行了比较，发现在设计PCHE 时，基于入口和出口点平均值的典型数据简化方法不适用于性能发生显著变化的传热过程，离散化方法是反映PCHE 特性变化的有效数据缩减方法。Yoon 等[16]针对高温气冷堆中PCHE 展开研究，发现根据实验数据得出换热器的效率是被高估的，在评估高温换热器性能时引入热损失部分，提高计算精度。Mortean 等[17]针对方形通道的交错流换热器展开研究，基于前人研究提出了一个数学模型来预测换热器的传热特性，对比分析实验数据和数学模型理论计算结果，发现Stephan 等[18]的关联式在模型中与实验数据比较时表现出最好的结果，特别是在低Reynolds 数时。Mortean 等[19]对不锈钢PCHE 的传热和压降进行了完整的分析，提出了一个预测换热器压降的模型，以水为两侧工作流体进行了72 次测试，发现Muzychka 等[8]提出的关联式与实验结果吻合较好；提出了一个压降模型，计算了设备芯、集管等部件的贡献，得出进口和出口集管对总压降的贡献最大，占50%以上。Sarmiento等[2,20]在已有研究的基础上，以文献中1482个数据点作为数据库，使用Churchill 等[21]提出的方法建立了一个适用于大多数常见非圆形管道的模型，模型计算结果与实验数据的最大误差小于30%；针对半圆形微通道提出了一种新的方法来考虑通道间翅片几何形状的变化，同时引入Yoon 等[16]提出的热损失概念，建立了PCHE 换热特性的预测模型，并将模型结果、实验结果、数值结果进行比较，结果表明三者吻合较好，综合误差小于8%。

由上述研究可以发现在流动与传热特性准则关联式的研究中，前者的研究主要针对摩擦特性与流动状态之间的关系，目的是获得求解Fanning 摩擦系数f的关联式，并通过摩擦系数间接得到压损；而后者的研究主要针对传热特性与通道结构、流动状态之间的关系，通常是获得求解Nusselt 数的计算关联式，然后间接计算对流传热系数、换热量等特性参数。然而，大量的研究都是针对特定工质、结构、工况等条件展开，得到的计算关联式大多只适用于特定情况，更换其中某一条件可能导致其不再适用。

因此，本文基于目前已有的研究，筛选出适用于层流换热的流动与传热特性关联式，并建立相关计算模型，通过文献中已公布的不同结构、工质、工况等条件下的实验测试结果与计算模型中不同关联式所得经验解进行对比，获得其中适用性最高的计算关联式组成计算模型。最后，提出一种PCHE换热核芯结构，对其进行两种工质（航空燃油RP-3与航空润滑油4050）对流换热的数值仿真与经验计算，对比数值解与经验解之间的精度，进一步验证计算模型的适用性。

1 理论模型

1.1 几何结构

对于PCHE换热核芯（图1），定义其整体结构尺寸为长L、宽W、高H；由Nc层冷板和Nh层热板层叠而成，每层板含有通道数M；冷、热通道的高为b、宽为w、栅格厚e、基底厚a，冷热流道结构相同，使用下角标c、h区分冷侧、热侧。对于本文PCHE几何模型所采用的半圆形流道，使用Sarmiento等[20]和Liu等[22]提出的理论将其等效为矩形结构，具体方法将在后文中详细叙述。

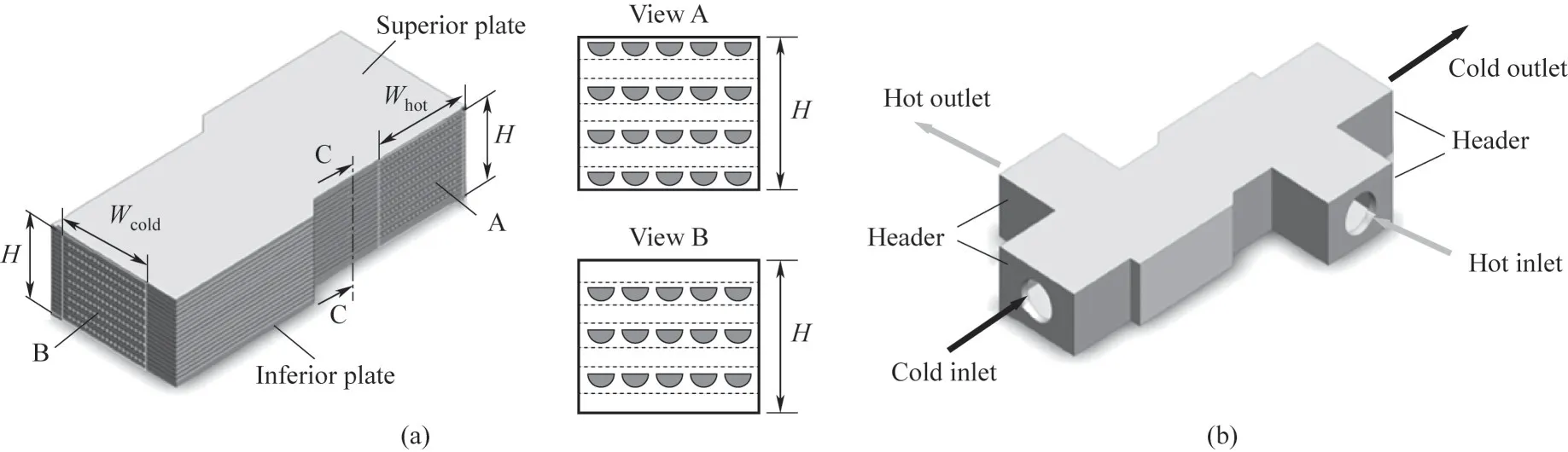
图1 PCHE结构示意图[2]Fig.1 Structure of PCHE[2]

基于PCHE 的几何参数，根据文献[23]，紧凑度α是传热面积与体积的比值：

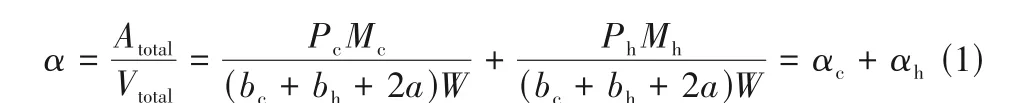
式中，Atotal为总传热面积，m2；Vtotal为换热器核心体积，m3；P为湿周，m。

孔隙度σ为自由流面积Afree与前缘面积的比值，表达式为[23]：

由式（3）可知，换热器的紧凑度α与孔隙度σ成正比，与当量直径d成反比。可见，为了提高紧凑度α（即更小的换热体积内具有更大的传热面积），就必须减少当量直径或增加孔隙率。

1.2 传热特性理论计算

对换热器内的换热过程进行简化处理来确定传热路径，以便进一步分析和讨论，有如下假设：微通道尺寸较小，忽略通道内的辐射和自然对流；固体具有恒定特性，流体不可压缩、性质无突变，且能以平均温度为基础表示；层流流动下恒定传热速率、稳态传热；流体均匀分布于各通道之间，具有均匀的流速剖面。

基于上述假设，热交换器的总传热系数UA（或总热阻1/UA）可以表示为[23]：

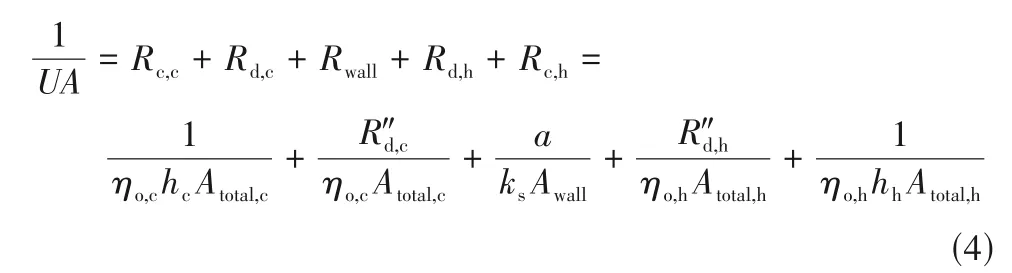
式中，Rc为对流热阻；Rd为污垢热阻；Rwall为基底导热热阻；R″d为污垢系数；ηo表示表面总效率；Awall表示平均壁面面积；h表示材料的传热系数；ks表示材料热导率。换热器中传热特性计算简化为翅片结构，如图2所示。

图2 传热计算简化示意图Fig.2 Simplified schematic diagram of heat transfer calculation

PCHE 的应用中，由于其通道孔径很小，需要保持工质洁净，不能有掺混杂质、局部结渣等问题造成微通道堵塞。在计算过程中，可以忽略污垢热阻的影响，式(4)可以简化为：

式中，χ表示效率参数。

式中，φ表示通道的宽高比，定义为通道最大边与最小边的比值；Red表示以当量直径为特征尺寸的Reynolds数，表达式为：

式中，ρ为流体密度；V为流速；μ为动力黏度；ṁ为流体质量流量。

上述表达式中，壁面热流和通道径向温度被认为是常数，是目前紧凑型热交换器的较好近似。经过上述过程可推导得到关于总传热系数UA（或总热阻1/UA）的求解式，其中重点需要求解的冷、热流体的对流传热系数（或Nusselt数），该值需要通过大量实验数据推导计算获得，许多研究者根据不同流动状态（层流区、过渡区、湍流区）提出了不同的Nusselt 数关联式。针对微通道内层流具有代表性的关联式如表1所示。

表 1 微通道内层流换热Nusselt数关联式Table 1 Nusselt number correlation of laminar heat transfer in microchannels

表1中8个Nu关联式均以当量直径作为特征尺寸，除此之外部分学者研究发现以截面面积的平方根A作为特征尺寸拟合得到的Nusselt数关联式模型同样可以取得极佳的计算精度，部分学者研究结果如下。

Muzychka等[8,30]评估了几种特征尺寸，对椭圆和矩形通道进行了比较，发现圆形通道和矩形通道的解基本上已经坍缩为单一值，并且在小长径比的极限下，椭圆通道和矩形通道的计算结果也趋于一致，可以清楚地看出，对于层流数据的无量纲化，横截面积的平方根比水力直径更合适。Muzychka 等基于截面面积的平方根A作为特征尺寸，提出Nusselt数关联式模型：

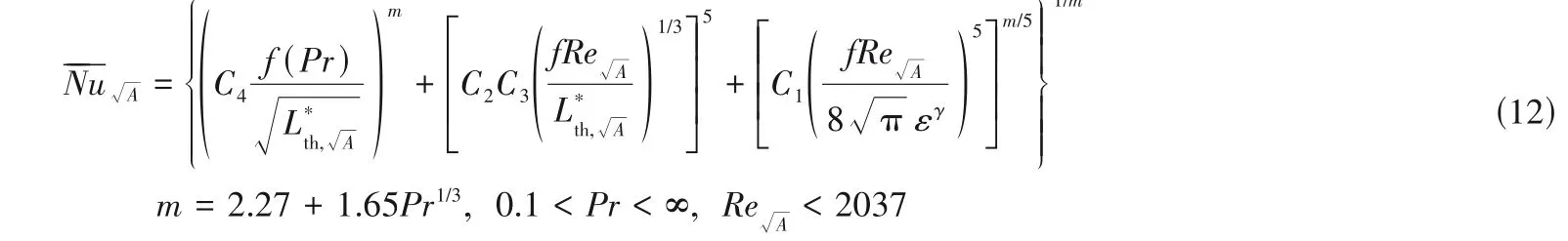
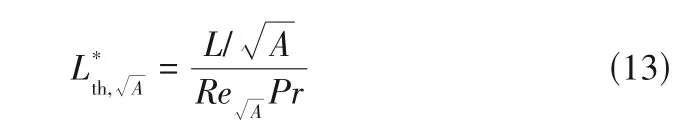
层流状态下的Fanning摩擦系数表达式为：

此外，常数C1和C3是热边界系数，而C2和C4取决于Nusselt数是局部值和平均值；f(Pr)是一个依赖Prandtl数的因子；γ是形状参数（表2）。

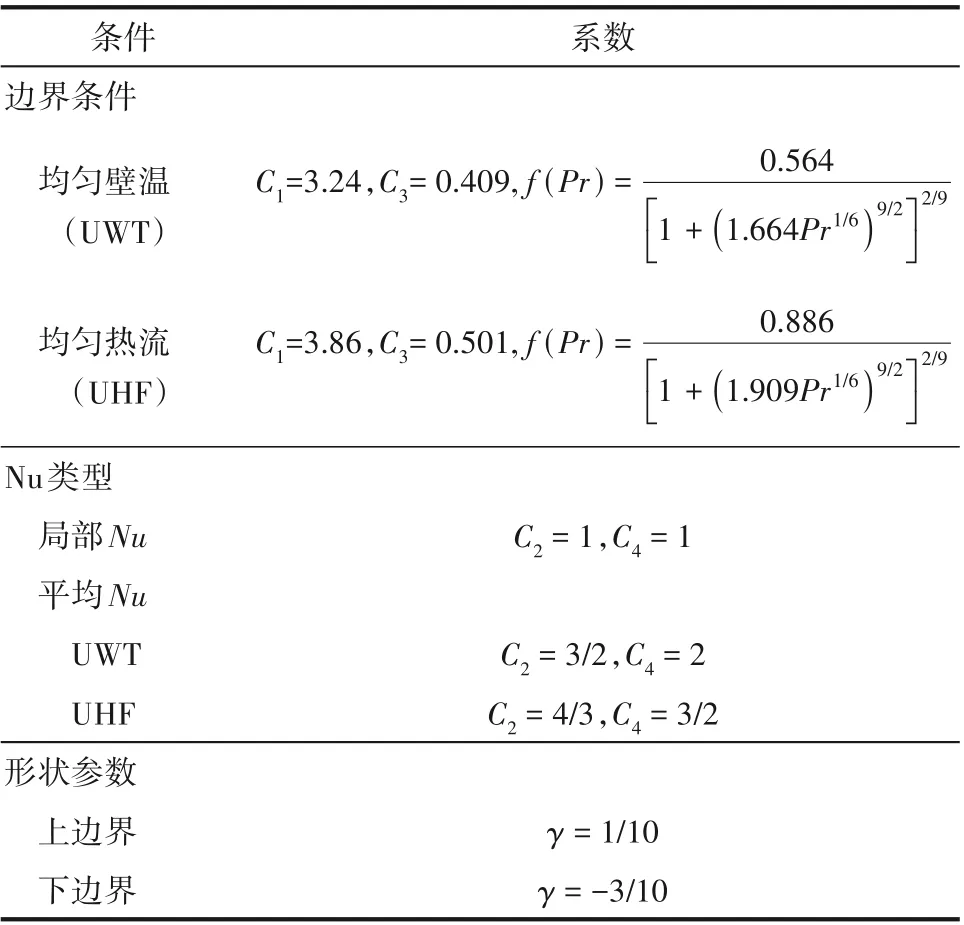
表2 关联式系数［20，30］Table 2 Correlation coefficient［20，30］

Sarmiento 等[20]使用Churchill等[21,31]提出的方法，建立了一个适用于大多数常见的非圆形管道的模型，该模型利用层流和紊流的换热表达式生成了一个过渡方程，表达式为：

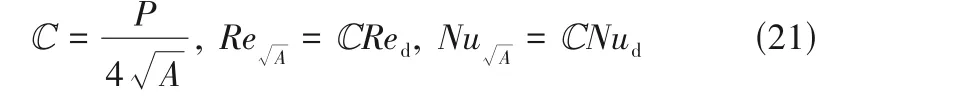
求得冷、热侧流体Nu后，间接推导对流传热系数h，然后再计算得到总传热系数UA，最后计算总换热量等性能参数区分与转换。基于本文的研究内容，采用LMTD 法、ε-NTU 法构建计算模型，介绍如下。

换热量是通过对数平均温差ΔTLM来确定，适用于热物性不发生较大变化且工况远离临界条件的情况[15,38-39]，当热物性会发生剧烈变化时，需要采用离散化方法[15,40-41]。本文属于前者，总热导率可表示为：

对于校正因子F的计算，不同流动形式的换热器取值有所不同，完全逆流的换热器的F值取1。对于混合交错流换热器，校正因子F的定义式为：

式中，C表示换热工质的热容量；Cmin表示冷、热工质热容量的最小值。

恒压下，工质比定压热容cp变化不剧烈时可视为常数，在忽略环境热量散失时总传热量Q可表示为：

式中，C*表示冷、热工质的热容量的最大值与最小值之比。不同流道布置形式效能ε表达式有所不同，本文主要涉及准逆流、非混合交错流。

逆流换热器效能ε的表达式[42]为：

根据Kuppan[37]、Shah 等[43]提出的解析表达式，非混合交错流换热器的效能ε为：

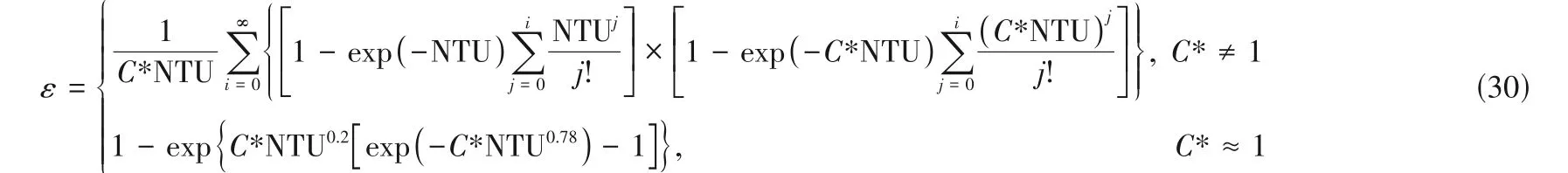
在换热器运行时，由于环境的影响其热损失可能很大。Yoon 等[16]考虑周围环境热损失提出了模型：

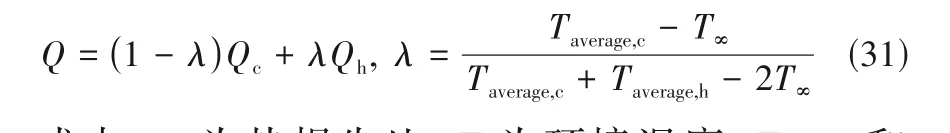
式中，λ为热损失比；T∞为环境温度；Taverage,c和Taverage,h分别为冷流体和热流体的平均温度。

1.3 流动特性理论计算

对于微通道换热器的流动特性的计算，本文基于现有文献中提出的相关实验关联式估算的换热器整体的Fanning 摩擦系数，然后通过摩擦系数间接求解得到换热器各个关键位置产生的压损。在进行压降计算前，进行如下假设：

（1）入口流量稳定；

（2）流体在每个通道中均匀分布；

（3）所有通道的几何形状相同；

（4）重力效应被忽略，换热器是水平定向的；

（5）流道通道的横截面为半圆形。

图3 为PCHE 在实验测量过程中可能会存在的压损分布示意图。由图可得，当前PCHE 中的压降大致可以分为三部分：①换热器核芯中的流动压降Δpcore；②通道入口突缩和出口突扩相关的压降Δpcontraction、Δpexpansion；③进口和出口流量分配集管中的压降Δpheader。

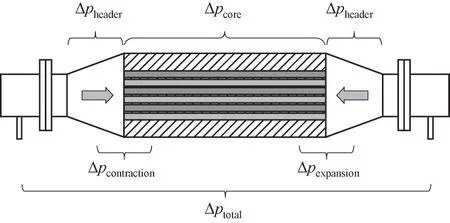
图3 压损分布示意图Fig.3 Schematic diagram of pressure loss distribution

其中，对于封头内部的压损暂没有相关实验数据，因此暂时忽略其影响，只针对换热核芯内的流动特性展开分析与讨论。所以PCHE 热侧和冷侧总压降可计算为：

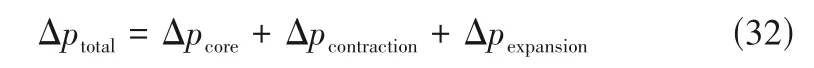
相关文献中PCHE 各部分的压力损失理论计算方法大致如下。

（1）换热器核芯中的流动压降

换热器核心中的压力损失由两部分组成：摩擦产生的压力损失Δpfriction、动量变化产生的压力损失Δpacceleration和通道折角产生的压力损失Δpangle。其中，摩擦损失同时考虑了表面摩擦和形状阻力效应，由流动面积变化引起的内部收缩和膨胀产生的任何额外损失（如有）也被纳入换热核芯摩擦损失项，表达式为：

式中，V表示具体体积；Vin和Vout分别在入口和出口温度和压力下进行评估。下角标in、out分别表示入口、出口；m代表平均。

Fanning 摩擦系数f基于有效壁剪切应力计算，由于通道内部的剪切应力无法通过实验等方法直接测量，使得对于微通道内Fanning 摩擦系数f的计算关系式没有统一的、普适性的实验关联式。许多学者基于现有的理论进行研究，致力于通过实验测量来拟合实验关联式来预测通道内部的摩擦损失，本文基于现有的研究内容，整理出一些应用相对较广的关于层流流动的实验关联式，如表3所示。

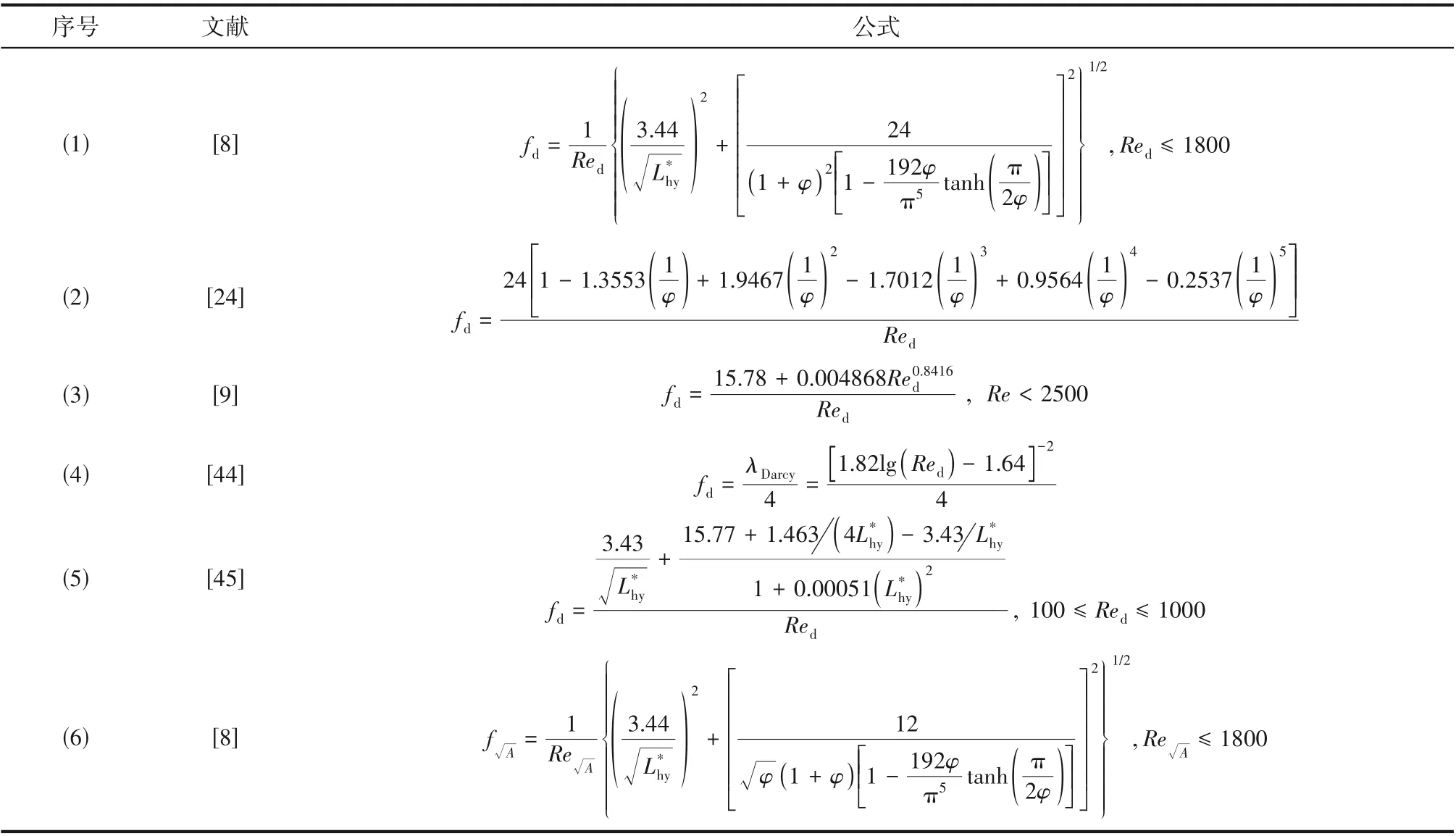
表3 微通道Fanning摩擦系数f的关系式Table 3 The Fanning friction coefficient f of the microchannel

由于换热核芯内的动量变化产生的压缩归因于流体被加热或冷却，导致换热核芯内的动量率变化或流动加速或减速效应。其中，正值表示流量加速时的压力降低，负值表示流量减速时的压力升高。由此产生的压降由式（35）给出：

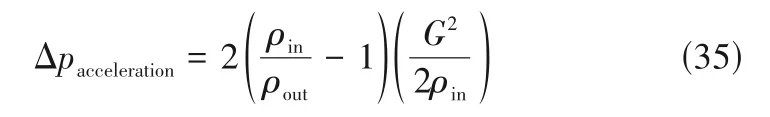
流体经过一个弯曲通道时，必然会在流体上作用一个向内的径向力，外壁面压力增大，在内壁面上有压损。在流动惯性的作用下，使得弯管和折管内侧往往会产生旋涡，造成局部压力损失，如图4所示。

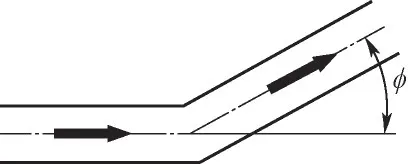
图4 通道内部折角Fig.4 Internal angle of channel

根据Darcy-Weisbach 公式，折管内局部阻力系数ζangle表达式为[46]：

（2）入口突缩和出口突扩相关的压降Δpcontraction、Δpexpansion

Kays等[47]分析评估了换热器核心区域的压降收缩和膨胀产生的影响，人为地将换热器的入口段的压降分成两个部分：①流动截面积发生变化导致压力损失，此过程不考虑摩擦作用；②突缩段的不可逆自由膨胀引起的压损（可以解释为：流体流过突然收缩断面，产生流动边界层分离，导致随着断面下游的速度分布发生变化，然后动量速率也发生变化，进而引起相应应力的变化，从而产生压力损失）。入口段压损仅因面积变化引起的压降由式（39）给出：

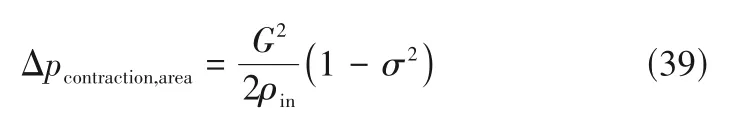
式中，G是换热器微通道（或管束）内质量速度，即核芯内质量流动速度；σ是核芯自由流动面积和横截面积之比，即孔隙率，也称收缩比。

对换热核芯入口压降的第二个贡献是与突然收缩和动量率变化后的自由膨胀相关的损失，收缩损失系数Kc乘以换热核芯进口处的动态速度头，可算出不可逆压降分量：

式中，Kc为收缩损失系数，是收缩比σ、Reynolds数Re和流动截面几何形状的函数。因此，换热核芯入口压降为：

对换热核芯入口压降的第二个贡献是与突然收缩和动量率变化后的自由膨胀相关的损失，收缩损失系数Kc乘以换热核芯进口处的动态速度头，可算出不可逆压降分量。

类似地，出口段的压损也可以分成两个部分：①流动截面积发生变化而引起的压损，此过程不考虑摩擦作用，其表达形式与入口侧压损相同；②突扩段的不可逆自由膨胀、动量变化等现象引起的压损[47]。出口段由于截面面积增加导致减速引起的压损升高为：

不可逆自由膨胀和突然膨胀后动量率变化相关的压力损失，由出口损失系数Ke乘以换热核芯出口处的动态速度头得出：

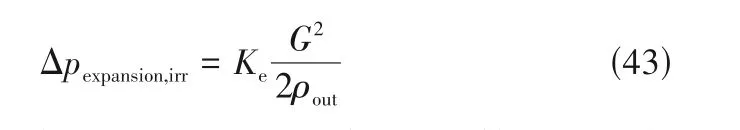
式中，Ke是突扩（或出口）压力损失系数，为膨胀比1/σ、Reynolds 数Re和流动截面几何形状的函数。因此，换热核芯出口处的压损为：

Kc和Ke是收缩段和扩展段几何结构的函数，在某些情况下还与管内Reynolds 数有关，原因在于管内速度的变化会引起动量变化，同时入口和出口的动量也会发生变化。在实际应用时，Kc和Ke中已经包含了速度分布变化与压力变化的影响，Kays 等[47]通过分析大量的实验结果证实了经验解的可靠性。Lee[48]提出了计算该系数的模型，表达式为：

在换热器的流动与传热特性计算过程中，通过上述实验关联式计算平均Nusselt 数与Fanning 摩擦系数，从而间接确定冷、热侧的对流传热系数h，然后通过进一步确定换热器整体的总传热系数UA（或总热阻1/UA），最后计算得到PCHE 的总换热量、效能、压损等特性参数。

2 精度分析

2.1 计算模型的构建

基于上述关于PCHE 中传热特性的理论计算，本文通过整理分析设计了一个用于预测换热器传热特性的计算模型，并且基于Matlab 语言编写了一个计算换热器传热特性的计算程序，框图如图5所示。

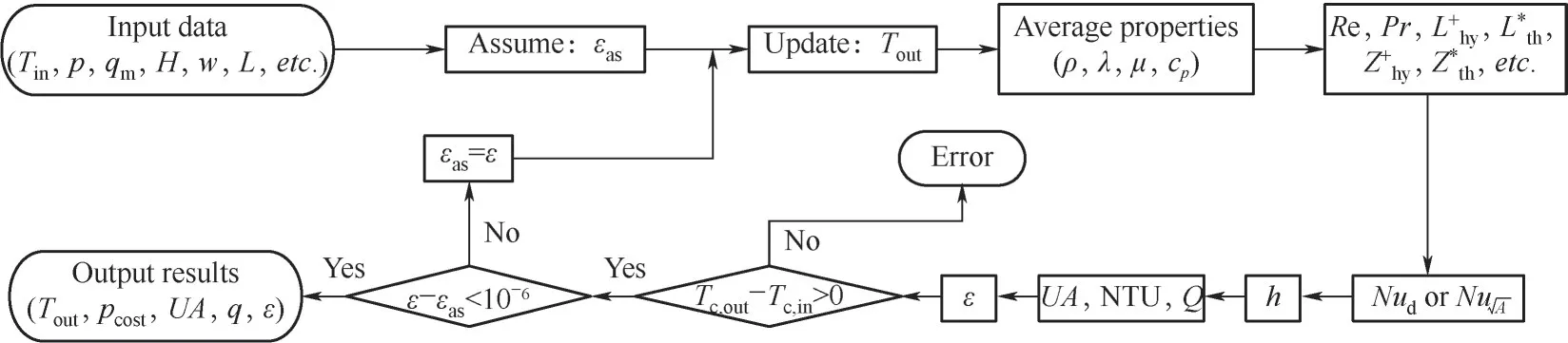
图5 程序框图Fig.5 Flow chart

由图5 可以看出传热特性计算过程，本文建立计算模型的基本流程为：

（1）输入数据。工质入口温度Tin、压力p、流量qm以及换热器整体的几何尺寸（H，w，L，a，e，等）；

（2）提出一个效能εas的假设值作为初始值，估算出口温度Tout；

（3）基于入口、出口温度确定特征温度，进一步计算流动工质的物性参数；

（5）基于平均Nusselt 数的计算关联式估算冷、热侧换热工质的Nu；

（6）通过Nusselt 数确定冷侧、热侧对流传热系数h；

（7）计算换热器的总传热系数UA（或总热阻1/UA）、传热单元NTU和总换热量Q；

（8）确定换热器的效能ε；

（9）判断冷侧入口温度和出口温度是否符合要求，即Tc,out-Tc,in＞ 0，符合则进行下一步计算，否则计算停止并报错；

（10）判断换热器效能ε与效能假设值εas之差是否小于10-6，若满足，进入下一步；若不满足误差要求，则令εas=ε，然后基于效能假设值更新出口温度，重复步骤(3) ～ (10)直到满足误差要求；

（11）输出计算结果，完成计算。

基于上述计算模型，可以通过理论计算的方式获得PCHE 的传热特性，但现有的关联式种类较多，无法直接判断哪一种关联式可以很好地适配本文所研究的问题，需要通过实验数据来进行进一步的筛选，本文通过已有文献中的实验数据，来确定精确度、适用性相对较高的传热计算关联式。

2.2 实验数据库构建

为了验证关于PCHE 的10 种传热经验关联式以及6 种流动经验关联式的精确度与适用性，本文基于文献[2,17,19-20,45,49-50]中与紧凑型换热器相关的实验数据构建实验数据库，一共选用了426 个数据点组成实验数据库（表4），其中包含逆流换热、交错流换热两种换热方式，换热工质有气/气换热、气/液换热和液/液换热三种组合。

表4 数据库相关组成及研究内容Table 4 Composition of database and research content

基于文献中所给出微通道的几何条件与边界条件，采用本文所建立的计算模型计算其相关工况下的传热特性获得经验解，然后将经验解与实验数据库中的实验解进行对比分析。在计算过程中，考虑到换热过程中由于温度和压力对于换热工质热物性的影响，采用开源热物性数据库CoolProp 进行相关工质物性的获取[51]来表征换热工质在相应工况下的热物性变化。

由于本文所采用相关数据的工况远离临界条件，预计工质不会出现热物性的剧烈变化。此外，为评估计算模型计算结果的精度，使用均方根误差（RMSE）来评估二者数据间的差异。RMSE 的计算公式为[2]：

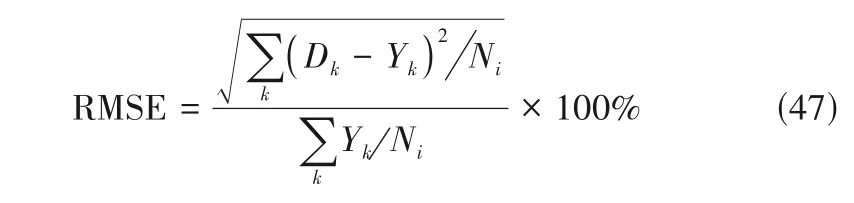
式中，Dk和Yk分别表示理论值和实验值；Ni表示可供比较的数据总数。

2.3 关联式精度分析与筛选

基于本文构建的计算模型，可以获得根据数据库文献所给出的紧凑型换热器几何特征与边界条件计算得到换热器的传热特性的经验解，其中包括出口温度Tout、效能ε、总传热系数UA（或总热阻1/UA）以及总换热量Q。下面进行计算模型所得经验解与数据库中的实验解之间精度的对比分析。

图6 显示了换热器出口温度Tout的经验解和数据库中实验解的对比。从图6(a)、(b)中可以看出，所有的经验关联式对于出口温度Tout的计算中绝大多数数据点的误差维持在10%以内，不同的关联式都表现出较好的计算精度。从整体来看，经验解与实验解的吻合度较好，尤其在高温段时精度明显较好，进一步对比低温区段[图6(c)、(d)]，可以看到尽管不同关联式计算所得经验解与实验解之间仍然存在不同的差异，但整体预测精度依然较好。相 对 来 说，Stephan 等[18]、Muzychka 等[8]和Sarmiento等[20]所提出关联式计算所得经验解更接近文献中的实验值。

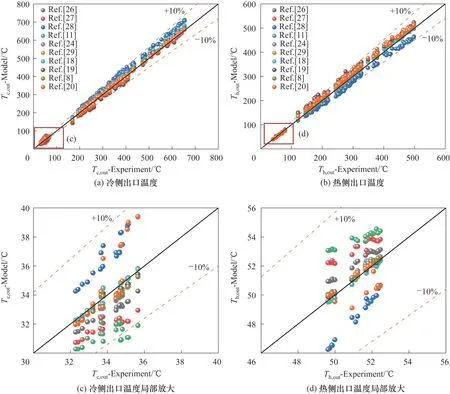
图6 出口温度Tout对比分析Fig.6 Comparative analysis of outlet temperature Tout

图7 给出了计算模型对换热器总传热系数UA（或总热阻1/UA）与总效能ε的计算结果和实验测试结果的对比。从图7(a)中对于总传热系数UA（或总热阻1/UA）的计算结果可以看到，Sarmiento 等[20]的关联式在低Re时的计算结果与实验结果吻合较好，计算结果的误差基本维持在10%以内；但随Re增大，即Re＞2300 后，计算结果明显低于实验测量值，误差增大到15%甚至更大。这种现象表明，该关联式在一定程度上低估了在高Re下对流换热的传热系数。类似地，其他关联式也表现出类似的情况。其中，Lee等[26]提出关联式的计算结果相比实验解明显偏小，低估了对流传热系数；与之相反，Peng等[28]提出的关联式的计算结果远远高估了对流传热系数UA的值，最大误差超过了30%；Muzychka 等[8]关联式在高Re下的计算结果的精度则更差一些。类似地，对比计算模型对于换热器效能ε的计算结果的误差，尽管Stephan 等[18]、Sarmiento 等[20]的关联式都存在一定的计算偏差，不过仅有少数的数据点计算误差达到30%，排除这些误差较大的点之后，二者的计算精度相比其余关联式的表现来看依然较好。其余几种关联式的表现大同小异，呈现出类似的误差分布。进一步对比上述对出口温度Tout经验解与实验解，从10种计算关联式中筛选出精度相对 最 高 的3 种 关 联 式，即Muzychka 等[8]、Stephan等[18]、Sarmiento等[20]的关联式。

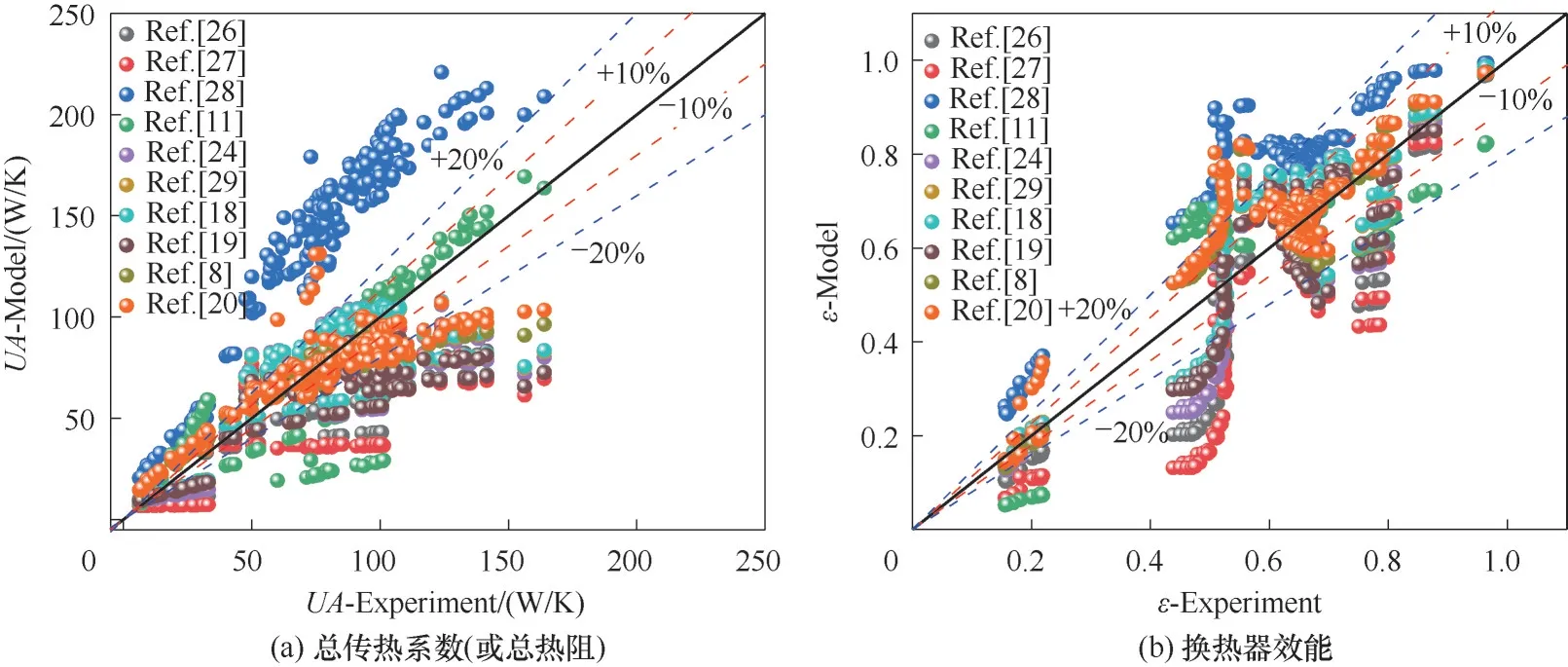
图7 总传热系数UA（或总热阻1/UA）与效能ε 对比分析Fig.7 Comparative analysis of total heat transfer coefficient UA (or entire thermal resistance 1/UA) and efficiency ε

图8 给出了本计算模型对换热器换热量Q的计算结果与实验测量值的对比。从图8(a)中可以看出，10 种关联式整体的均表现出相对较好的计算精度，虽然其中有个别数据点的误差较大，不过绝大部分数据点的计算误差保持在20%以内。选取数据库中局部的一些数据点进行对比分析[图8(b)～(d)]，可以看出一些关联式在换热量和较低时精度明显变差，比如Lee 等[26]、Grigull 等[27]提出的关联式。与之相反，Stephan等[18]、Sarmiento等[20]提出的关联式尽管在一部分数据点上计算存在较大的误差，但计算精度仍在可接受范围，无论是整体数据点还是局部数据点都表现出较好的计算精度。

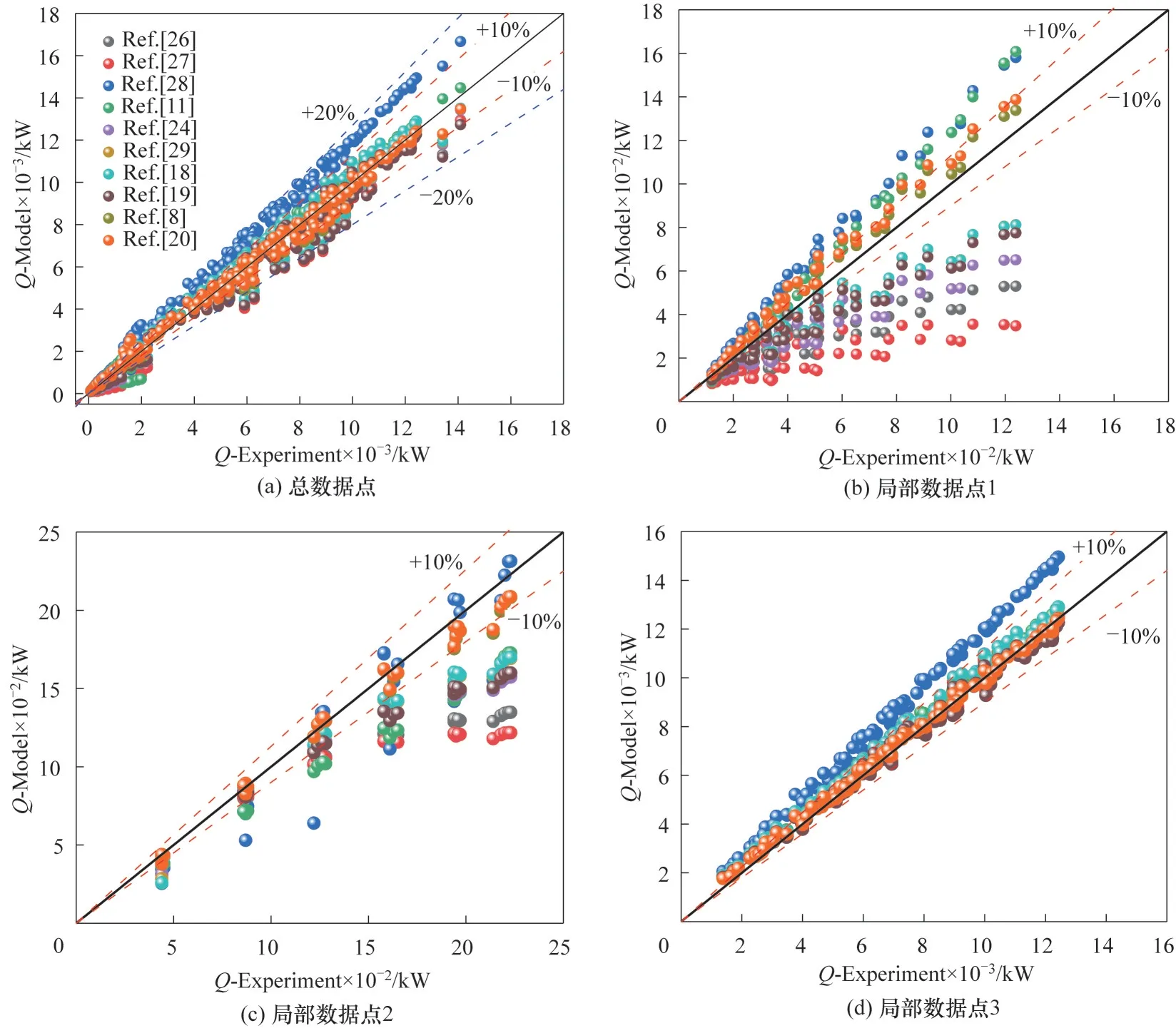
图8 总换热量Q对比分析Fig.8 Comparative analysis of the total heat exchange amount Q

经过上述对比分析，可以得出本文建立的计算模型可以较好地预测换热器的传热特性，其中，Stephan 等[18]、Sarmiento 等[20]提出的关联式很好地预测了不同工况下换热器传热特性。前者虽然是基于圆形通道的实验拟合而得到经验公式，但对于非圆形通道的实验预测依然保持很好的预测精度；后者尽管在较低Re时会过分估计对流换热量，但随着Re的增加，误差逐渐减小，计算结果的精度也同步提高。因此，通过对比实验测量值与计算模型的理论值，可以初步确定计算模型采用Stephan 等[18]或者Sarmiento 等[20]提出的计算关联式来预测PCHE 的传热特性。

图9 所示为模型计算结果与数值仿真结果的对比分析，可以看到除了Fried 等[44]提出的关联式误差较大，Shah 等[24]的计算误差稍大，其余关联式均和数值模拟结果吻合很好，误差基本保持在10%以内。从图中可以看到，预测模型与数值仿真结果不仅变化趋势保持一致，数值也基本吻合，由此可以进一步说明前面针对实验测量值偏大的分析是正确的。

图9 换热器Fanning摩擦系数f与数值仿真值对比分析Fig.9 Comparison and analysis of Fanning friction coefficient f of heat exchanger with numerical simulation

图10 显示了本文计算模型对换热器Fanning 摩擦系数f的计算结果与实验测量结果的对比，可以看到除了Fried 等[44]提出的关联式预测结果很差，Red＜ 2000 时的计算结果远远偏离了其余三种关联式的计算结果，而2000 ＜Red＜4000 时与其余关联式又有所重合，但下降速度则较低。其余关联式的预测曲线相比实验测试结果的变化趋势基本一致，但数值之间仍有一定差距，其中原因可能在于通道内部转折弯角处出现二次流，增大了压力损失，同时换热器的加工过程中出现了部分通道的畸变导致换热器内部出现局部的收缩和膨胀导致压力损失，从而使得实验测量值大于模型计算值。相比之下，Kim 等[14]、Muzychka 等[8]提出的关联式所得到的经验解与数值解更为接近，不仅误差小而且趋势吻合较好，二者对于实验解的预测尽管有一定的误差，但是整体的变化趋势十分接近。因此，通过对比实验测量值、数值仿真值与计算模型的理论值，可以初步确定计算模型采用Kim 等[14]或Muzychka 等[8]提出的计算关联式来预测PCHE 的流动特性。

图10 换热器Fanning摩擦系数f与实验测量值对比分析Fig.10 Comparison and analysis of Fanning friction coefficient f of heat exchanger with experimental measurement

综上所述，通过对比实验测量值与计算模型的理论值，可以初步确定本计算模型采用Stephan等[18]、Sarmiento 等[20]提出的关联式来计算PCHE 的传热特性，采用Kim 等[14]、Muzychka 等[8]提出的关联式计算流动特性。

3 仿真分析对比

3.1 边界条件与仿真模型

前文依据本文建立的计算模型，分析了不同Nusselt 数的经验关联式对于微通道换热器传热特性的预测情况，对比了经验解与实验解之间的精度分布，筛选出2 种计算关联式对于层流区域内对流换热计算精度和适用性表现较好。接下来，本文针对一种印刷板式微通道换热器（PCHE）的换热核芯进行仿真分析，该结构由冷侧、热侧换热板结构组成，如图11所示。基于上述计算模型以及筛选出的经验关联式对该换热核芯进行传热特性的求解，对比分析经验解与数值解的误差。

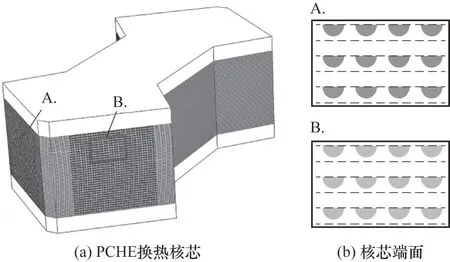
图11 换热核芯结构示意图Fig.11 Structure of heat transfer core

从图11中可以看出，该换热核芯为两种换热工质的对流换热，在换热板的中间部分为主要的换热形式，即准逆流；在换热板的两端（即入口、出口）为交错流。其中，两种换热工质分别为航空燃油RP-3以及航空润滑油4050，在数值仿真与模型计算时，前者的热物性采用Deng 等[52-54]和Cheng 等[55]的实验测试结果来表征，后者的物性依据杨九高[56]给出的物性关系式来表征，两种换热工质物性均随温度变化，采用多项式拟合，拟合多项式如表5所示。

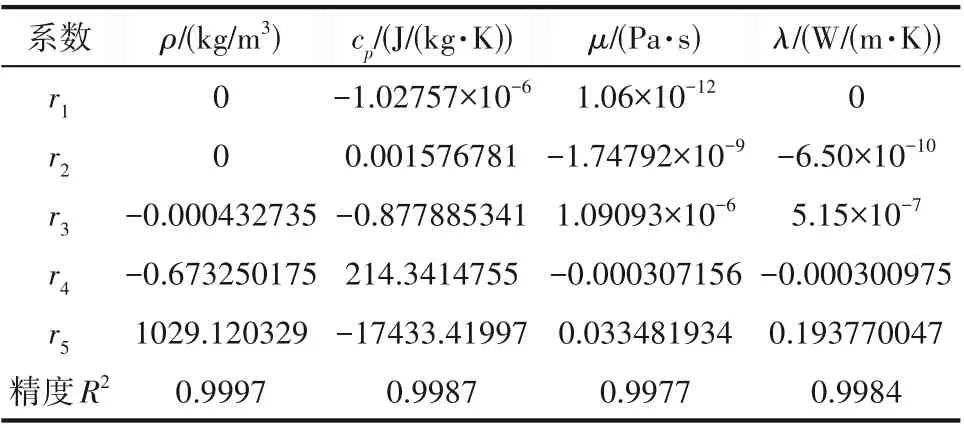
表5 航空燃油RP-3拟合多项式［52-55］Table 5 Fitting polynomial of aviation fuel RP-3［52-55］

航空润滑油4050的物性关系式为：密度ρ

式中，ρ表示密度，kg/m3；cp表示定压比热容，J/(kg·K)；λ表示热导率，W/(m·K)；υ表示运动黏度，mm2/s；T表示温度，K。

换热板片通常采用化学刻蚀的方法进行加工，加工得到的通道横截面为接近半圆结构的椭圆形，在理论研究时会对该结构进行等效处理，本文采用Sarmiento 等[20]和Liu 等[22]提出的理论为基础，将半圆形截面微通道等效为一种矩形结构，如图12所示。

等效后的矩形翅片的平均厚度x′、y′可以根据截面积来进行估计，二者的表达式为：

式中，R表示近似圆形通道的半径，m；AT1、AT2分别表示半圆形翅片的冷侧截面积、热侧截面积，m2；其余参数见图12，详细推导过程见文献[2]。

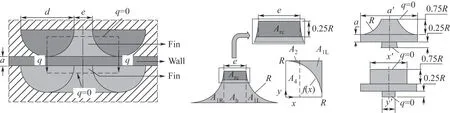
图12 半圆形微通道截面示意图[2]Fig.12 Semicircular microchannel cross section[2]

由于该PCHE 换热核芯结构中换热板片数量较多，整体数值模拟显然是十分困难的，将会耗费大量的计算资源和时间。可以发现换热核芯结构呈现出周期性分布，即核芯部分以一层冷侧换热板与一层热侧换热板组成一个周期单元周期性分布。因此，抽取其中一个换热单元作为仿真对象，PCHE换热核芯的周期换热单元以及换热单元边界类型如图13所示。

图13 换热单元及边界类型Fig.13 Heat transfer unit and boundary type

其中，换热板片的结构参数见表6，换热单元的边界类型有：

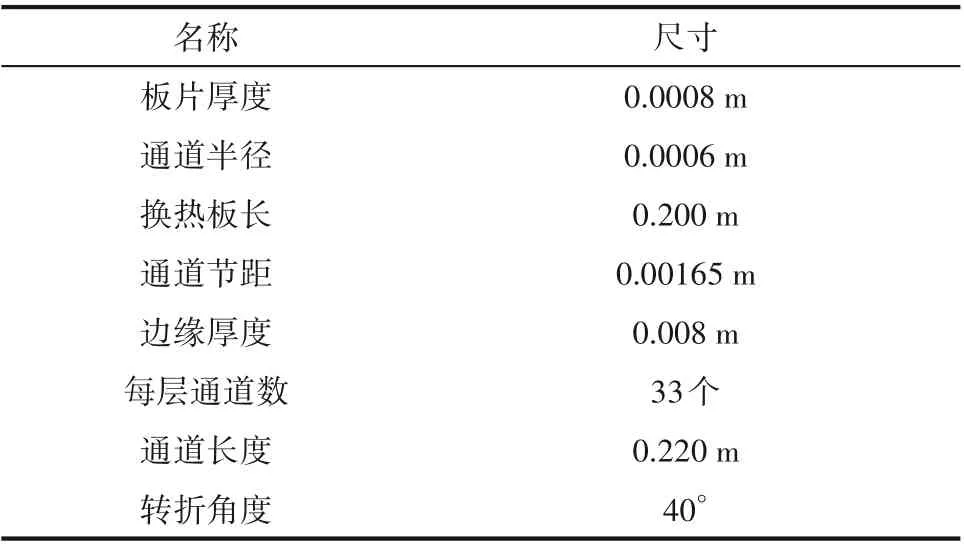
表6 换热板片几何尺寸Table 6 Heat exchange plate geometry

（1）入口边界 边界类型为速度入口（表7），并且背压为3 MPa；

（2）出口边界 出口边界类型为压力出口，背压为3 MPa；

（3）周期边界 换热单元上下两个面；

（4）绝热边界 通道出口处固体材料的截面；

（5）恒温边界 通道入口处固体材料的截面，温度等于来流温度；

（6）对流边界 外侧，对流传热系数为8 W/(m2·K)，环境温度为298.15 K。

对换热单元模型进行网格无关性验证分析，验证结果如图14所示。随着模型网格数量的增加，换热单元出口速度不断下降逐渐趋向于一定值（即0.22 m/s），但网格数量超过2200 万个后，模拟结果基本保持恒定，以此确定本模型数值模型时的网格数量为≥2200万个。

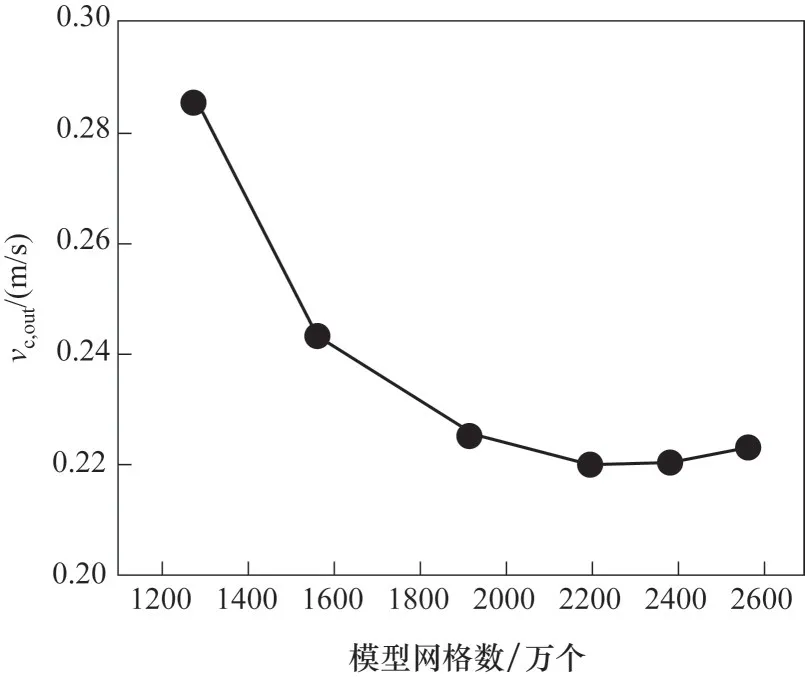
图14 网格无关性验证Fig.14 Grid independence verification

确定换热单元以及其边界条件后，基于入口Reynolds 数均低于2300，求解模型选择层流模型（Laminar）。为保证求解精度，采用双精度求解计算，求解算法采用Coupled 算法的二阶迎风格式进行求解，残差设置为1×10-10，迭代步数设置在2000步左右。如果模拟时出现回流现象，则先使用Simple 算法的一阶迎风格式进行求解，在计算基本收敛且回流现象消失，即为高阶求解建立初场，然后再使用Coupled 算法的高阶形式进行求解来保证求解精度。

3.2 数值解与经验解精度分析

基于建立的PCHE 周期换热单元，针对相应的工况开展数值仿真和解析计算的结果对比分析研究。工况安排见表7，其中热侧换热工质航空润滑油4050的入口温度和速度是一个恒定值，相对发生变化的只有冷侧换热工质航空燃油RP-3，其中入口流量的范围为1.0～5.0 m3/h，入口温度的范围40～80℃），合计45 组种工况开展相应的数值仿真和经验公式计算。

表7 工况分布Table 7 Working condition

在进行解析计算时则依赖于本文所建立的计算模型来预测换热单元的传热特性，本文建立的计算模型最终确定采用Stephan 等[18]、Sarmiento 等[20]提出的关联式来计算PCHE 的传热特性，在进行解析计算时将同时采用上述候选关联式进行计算，并对比不同关联式的计算模型的经验解与数值仿真结果的数值解之间的误差分布。

图15给出了换热单元冷、热侧换热工质出口温度的数值解与两种关联式的经验解之间的对比结果，从图中可以看出，两种关联式对换热工质出口温度的预测均存在一定的偏差，不过偏差基本都保持在10%以内，进一步证明本文研究结论的正确性，侧面说明两种关联式对于换热器的传热特性预测具有一定的指导意义。对比而言，虽然Stephan等[18]提出的关联式仅适用于层流，但其无论是对于冷侧工质，还是热侧工质的求解结果的连续性相对更好；相反，Sarmiento等[20]提出的关联式同时覆盖层流、过渡区以及紊流，虽然其适用范围更广，但在本文所研究内容中其适用性则相对较差，可以看出其求解结果不稳定，对于热侧工质出口温度的预测结果尤为明显。因此，对于本文所研究的相关内容，Stephan 等[18]提出的关联式显然更具实用性。进一步分析，由Stephan 等[18]提出的关联式对于冷、热侧换热工质的求解结果与数值仿真结果的对比可以看到经验解相较于数值解明显偏低[图15(a)]，经验解相较于数值解明显偏高[图15(b)]。初步分析，其原因在于数值仿真计算时，默认求解过程是理想的，对于很多不可控因素的影响进行了忽略，比如环境温度、加工精度等，然而Stephan 等[18]提出的关联式是基于实验测试结果进行拟合而获得，所以使得计算关联式的求解结果相较于数值仿真的理想结果偏低。

图15 出口温度的数值解与经验解对比Fig.15 Numerical solution of outlet temperature compared with empirical solution

在确定传热特性的计算关联式之后，在此基础上对比分析采用Kim 等[14]、Muzychka等[8]提出的关联式计算流动特性的经验解与数值仿真结果之间的偏差，图16 给出了换热器压损与Fanning 摩擦系数的经验解与数值解的对比结果，由于本节中仅有冷侧换热工质的温度和流速发生变化，而热侧换热工质保持恒定，因此只对冷侧换热工质的流动特性进行了对比分析。从图16(a)中可以看到，两种关联式对于换热器冷侧压损pcost的计算结果与数值仿真结果吻合度表现很好，二者误差均在10%以内，只有在整体压损较小（或入口流速较小）时存在相对较大的偏差，不过整体而言二者的吻合度、稳定性的表现均很好。进一步比较可以发现，Kim 等[14]提出的关联式与仿真结果的吻合度相较于Muzychka 等[8]的模型更高一点，不过二者的误差量级基本一致。图16(b)中给出了冷侧Fanning 摩擦系数的经验解与数值解之间的对比分析，其结果表现与压损pcost的表现基本一致，整体误差均维持在10%以内，并且随着流速的增加两种关联式的预测结果与数值结果越接近，相对而言Kim 等[14]提出关联式的表现略胜一筹。

图16 pcost 和 f数值解与经验解对比Fig.16 Comparison of numerical and empirical solutions of pcost and f

综上所述，通过对比采用Stephan 等[18]、Sarmiento等[20]提出的关联式对于传热特性的经验解和采用Kim 等[14]、Muzychka等[8]提出的关联式对于流动特性的经验解与数值仿真结果所得的数值解之间的精度，可以得出，Stephan 等[18]与Kim 等[14]提出的关联式对于本文换热单元的传热与流动特性的预测精度相对最高。

4 结 论

本文从理论计算的角度出发，基于现有的研究成果建立了PCHE 的经验解的计算模型，对比分析现有研究中提出的传热与流动特性的计算关联式，筛选出精度相对最高的关联式，并针对一种PCHE结构流动与传热特性进行了数值仿真与计算模型求解，对比分析了数值解与经验解，得出以下结论。

（1）基于现有研究成果，以PCHE 整体流动与换热特性的理论计算出发选取目前研究文献中所给出的关于层流Nusselt 数以及Fanning 摩擦系数的计算关联式，建立了较为全面的用于预测PCHE 流动与换热特性的计算模型。

（2）基于现有文献中关于层流的实验研究构建了实验数据库，对比分析具有代表性的关联式的经验解与实验解的精度，并确定采用Stephan 等[18]、Sarmiento 等[20]提出的关联式来计算PCHE 的传热特性，采用Kim 等[14]、Muzychka 等[8]提出的关联式计算流动特性。

（3）基于一种PCHE 核芯结构，选取换热单元作为研究对象进行数值仿真和计算模型计算，然后对比分析了流动与传热特性的数值解与经验解之间的误差分布，绝大多数点的误差在10%以内，验证了本文提出计算模型在理论求解中的准确性与可信度。此外，Stephan 等[18]与Kim 等[14]提出的关联式对于本文换热单元的传热与流动特性的预测精度相对最高。