光伏经新能源同步机并网小干扰模型及次同步振荡抑制作用

2022-02-18黄永章付文启武倩羽李晨阳

华北电力大学学报(自然科学版) 2022年1期

管飞，黄永章,2，杨鑫，付文启，武倩羽，李晨阳

(1.新能源电力系统国家重点实验室(华北电力大学)，北京 102206；2.华电(烟台)功率半导体技术研究院有限公司，山东烟台 264010)

0 引言

近年来以光伏和风电为代表的新能源发展势头迅猛，与此同时，各国因新能源机组并网引发的振荡问题也频繁发生[1，2]。2009年，美国德州某双馈风机群与串补装置间发生频率约20 Hz的次同步振荡(subsynchronous oscillation, SSO)事故，造成大量风机脱网[3]；2015年，我国新疆哈密地区也出现以直驱风机为主导的次同步振荡现象[4]，新能源场站的次同步振荡问题引发工业界的广泛关注。

针对新能源场站出现的SSO问题，目前国内外的研究大多集中于风电场，少有文献研究光伏电站的次同步振荡问题[5]。我国大规模光伏电站通常位于负荷消纳能力较低、电网结构薄弱的内陆地区，需通过长距离输电线路及串补装置并入主网，电网的阻抗耦合效应将对电力电子换流器的稳定性产生影响[6]。一旦发生振荡事故，会造成大规模光伏电站脱网从而威胁电网安全稳定运行，因此需对光伏电站的SSO问题加以重视[7]。文献[8]基于阻抗分析法，分析了连接弱电网时光伏系统SSO的产生机理与系统参数的影响特性。文献[9]在弱交流系统下建立了多光伏发电系统并联运行的小信号模型，采用特征值分析法分析了电网强度以及控制器参数对系统运行稳定性的影响。文献[10]建立了降阶后的光伏并网小干扰模型，并采用特征值法分析了系统振荡模态及其对状态变量的灵敏度。文献[11]借鉴复转矩系数法分析了不同串补度对光伏控制器阻尼的影响，并得到了控制器阻尼随串补度增加逐渐被削弱的结论。文献[12]结合算例分析了风光混合电场并网系统的数学模型，并通过附加阻尼控制器来提升系统阻尼，从而抑制SSO。

上述对于光伏电站SSO的抑制方法大多基于控制器参数的调节或增加附加阻尼控制，系统中电力电子特性并未改变。且实际电网运行情况复杂多变，电网结构随新能源机组及串补装置的并入而不断变化，制定一组可以适应不同振荡情况的控制器参数较为困难。光伏并网系统振荡问题的本质在于缺乏足够的阻尼，由于不具备同步机组的高阻尼特性，在发生SSO时，系统无法依靠自身阻尼抑制振荡，导致功率振荡发散，使得保护系统动作，造成新能源机组脱网[13，14]。因此若能将光伏并网系统赋予传统同步电机的阻尼特性，则可极大的改善系统振荡。

针对高比例新能源电网存在的频率及电压稳定问题，已有研究基于同步电机理论提出了新能源采用MGP并网的新型并网方式[15-17]。将同步机的惯性支撑与自发无功响应特性赋予新能源电场，可有效提高大规模新能源电网稳定性。但目前对于振荡特性的研究仅局限于双馈风机通过MGP并网的小干扰稳定[18]，MGP对光伏并网发电系统振荡特性的影响并未进行深入研究。

基于此，文章研究MGP在抑制光伏电站SSO方面的作用。首先分析了MGP系统的阻尼特性；然后考虑光伏系统与MGP系统电气量的对接关系，建立了光伏通过MGP并网的线性化小干扰模型，采用特征值分析法研究了MGP对光伏并网系统振荡模态的影响，并通过算例比较了控制器参数在两种并网方式下对系统次同步振荡模态的影响特性；最后通过PSCAD/EMTDC软件进行了仿真验证，所得结果与理论分析具有较高的一致性。

1 MGP并网系统的阻尼特性

1.1 MGP并网结构

光伏通过MGP系统并网结构如图1所示，光伏组件输出直流电至变频器，变频器根据控制系统所采集到的电网侧电气量进行电量变换，输出三相交流电驱动同步电动机旋转，同步电动机通过机械轴与同步发电机相连接，并带动同步发电机旋转，配套的两台励磁系统可维持机端电压稳定，实现并网操作。

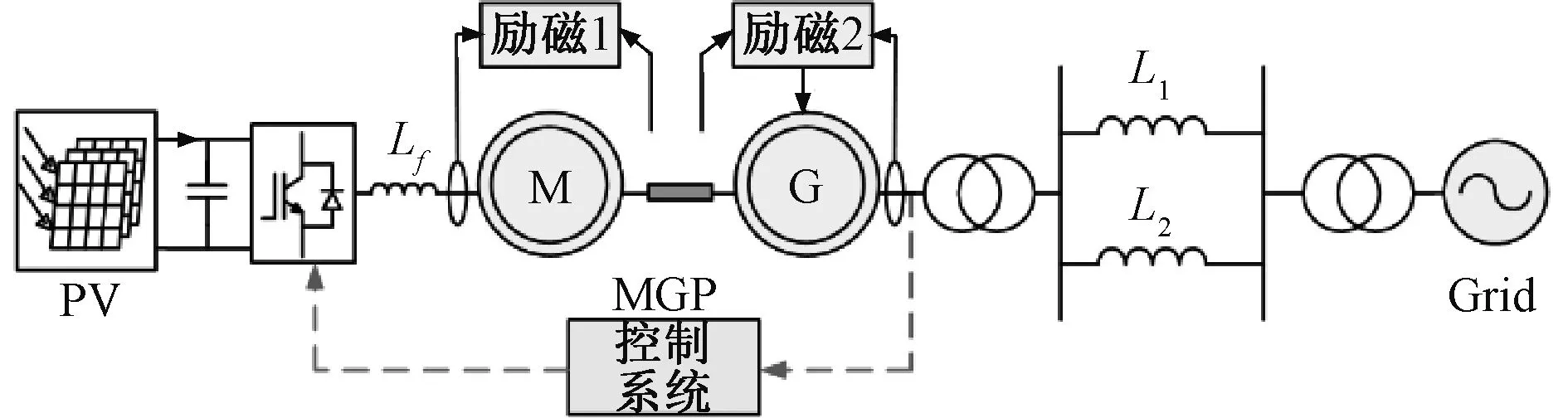
图1 光伏通过MGP并网结构图Fig. 1 Diagram of photovoltaic grid-connected via MGP

MGP在运行过程中的能量变化形式由电能转化为机械能再转化为电能，已开展的研究表明MGP的损耗主要与电机的设计结构及电机参数有关。实验室5.5 kW的MGP系统在额定参数下的运行效率约为91.6%，可有效实现能量传输。此外，MGP的惯性响应与自发无功特性可在一定程度上节约新能源场站在储能及无功补偿方面的投资，耐压、耐流能力也可节省高、低穿改造费用，从而有效降低MGP的投资成本。

1.2 MGP并网系统阻尼特性

受扰动后MGP电磁力矩的变化量ΔTeMGP可分解为同步转矩和阻尼转矩：

(1)

式中：ΔδMG为MGP功角变化量，ΔωMG为MGP转速变化量，TS为同步转矩系数，TD为阻尼转矩系数。与ΔδMG同相位的分量为同步转矩分量，与ΔωMG同相位的分量为阻尼转矩分量。

光伏电场采用MGP并网方式后，可使得新能源电网从以电力电子器件为主导的振荡形式逐步过渡为以同步机为主导的振荡形式。新型并网方式下的光伏系统稳定性主要取决于同步转矩分量和阻尼转矩分量，振荡问题的本质在于缺乏足够的阻尼转矩分量。

MGP的阻尼包括转子机械轴旋转引起的机械阻尼与磁通变化引起的电气阻尼。机械阻尼与电机旋转过程中的摩擦系数有关，不易改变，因此在实际运行过程中主要考虑电气阻尼的影响。MGP的电气阻尼具有叠加效果，同容量下的MGP阻尼比ζMGP大约为同质量块的单个发电机的1.47倍[15]。且配备的两套励磁系统均可对阻尼效果产生影响，若充分研究励磁系统间的相互作用，则可进一步提高MGP阻尼效果，维持振荡稳定。

另外，用于连接MGP两电机的机械轴使得两侧电气系统相对独立，可在一定程度上弱化光伏系统源端控制器与电网侧阻抗的耦合效果，减少次同步振荡发生几率。

2 光伏采用MGP并网的小干扰建模方法

图2为光伏通过MGP并网的结构及控制框图，MGP串联于滤波电感线路后，两套励磁系统分别对两台电机施加励磁控制，功率控制策略采用PQ解耦的矢量控制。由于隐极式同步电机电磁转矩与q轴电流呈线性关系，因此通过对q轴电流的有效控制实现有功功率的稳定传输[16]。

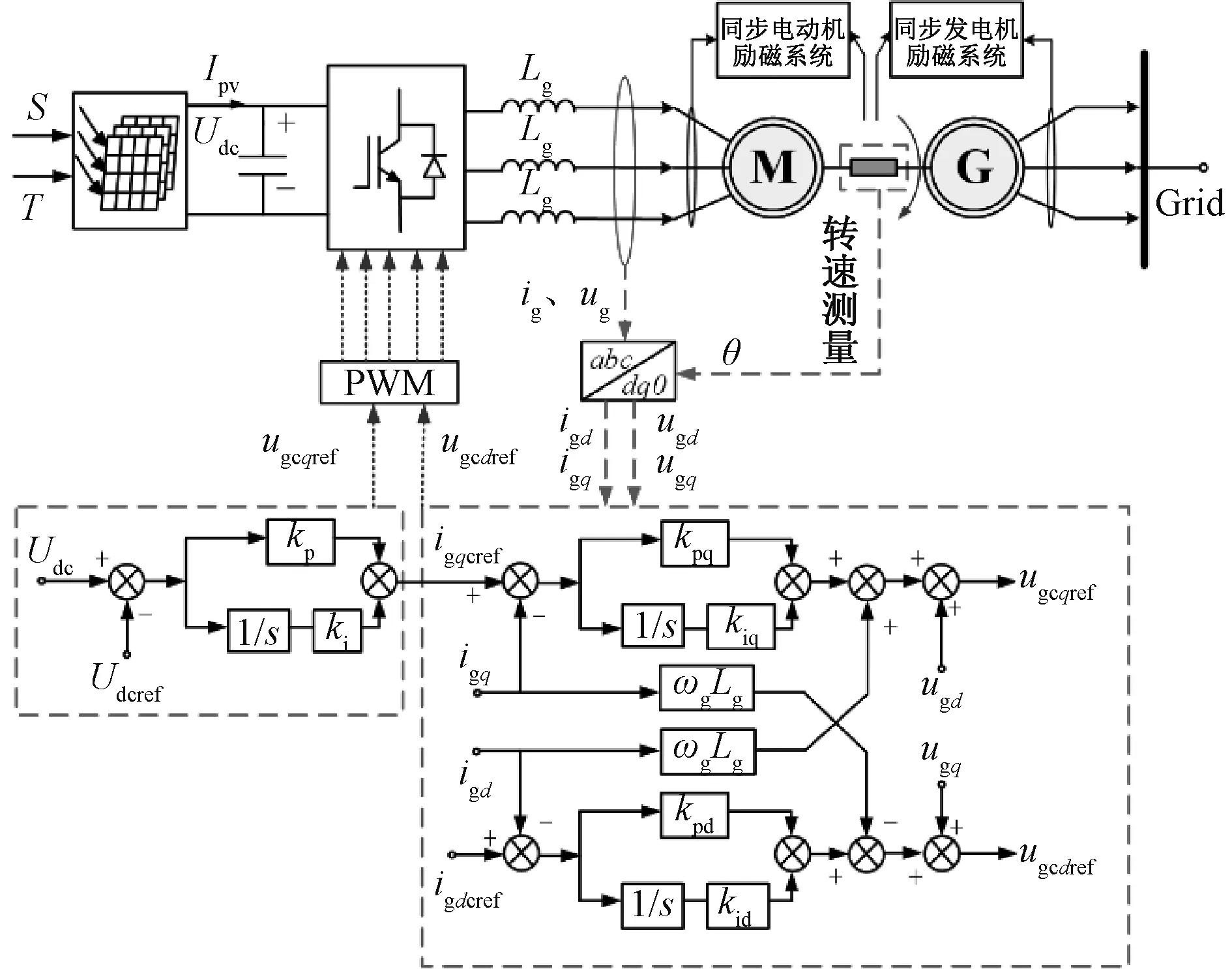
图2 光伏通过MGP并网控制框图Fig. 2 Diagram of photovoltaic grid-connected via MGP and its control system

2.1 MGP系统小干扰模型

MGP中两台电机构造完全一致，同步电动机与同步发电机同轴连接，机械转矩与转子转速均相同，因此MGP转子运动方程可由两电机的运动方程叠加表示为

(2)

式中：Δωr为转速偏差，H为MGP中单台同步机的惯性时间常数，ΔTeM和ΔTeG分别为电动机和发电机电磁转矩的变化量，KDM和KDG分别为电动机和发电机的阻尼系数，ω0为转速基准值。

MGP中每台电机的功角关系如图3所示。

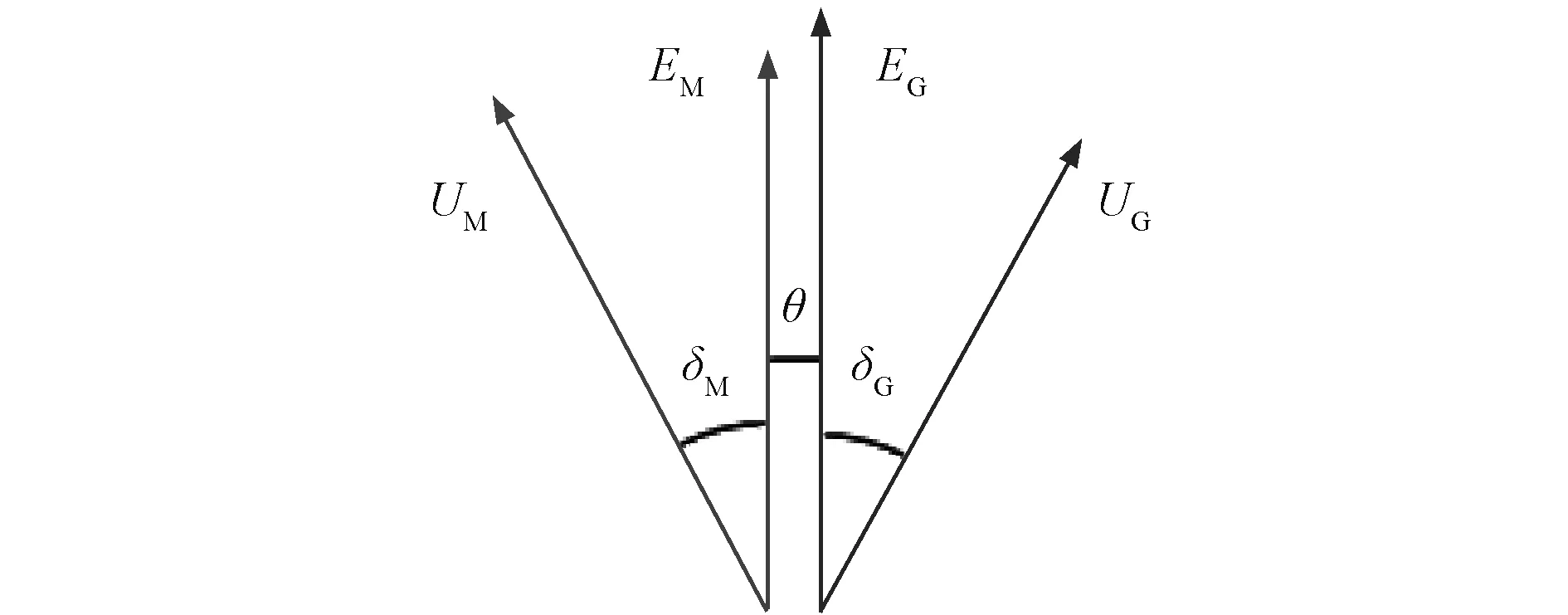
图3 MGP功角关系图Fig. 3 Power angle characteristics of MGP system

图3中UM、EM分别为同步电动机端电压和内电势，UG、EG分别为同步发电机端电压和内电势，δM、δG为电动机与发电机功角，θ为两电机轴之间转子位置差，通常为一固定值。

根据同步机功角特性，MGP中两同步机的传输功率可分别表示为

(3)

式中：TeM、TeG分别为电动机与发电机的电磁功率(标幺制下电磁功率与电磁转矩相等)，xdM、xdG分别为电动机与发电机d轴电抗。

标幺制下，MGP在旋转过程中的功率关系可表示为

TeM-TeG=Tloss

(4)

式中：Tloss为MGP系统旋转过程中的机械损耗，为一常数。

根据能量守恒关系，在忽略电机功率损耗的情况下，电动机与发电机的传输功率时时刻刻相等，功角变化趋势也相同。结合公式(3)，即电动机的功角δM增加时，发电机的功角δG也会同步增加。为了将机械轴两侧的电气量相联系，并便于后续建模分析，本文将两电机功角变化量之和定义为MGP的功角变化量ΔδMG，并将ΔδMG作为状态变量来替代ΔδM与ΔδG。如公式(5)所示：

ΔδM+ΔδG=ΔδMG

(5)

将公式(4)线性化，并考虑励磁系统动态时，MGP两电机电磁转矩变化量可表示为如下形式：

(6)

式中：K1M、K1G、K2M、K2G分别表示与两电机参数和磁链初始条件有关的常数，ΔψfdM和ΔψfdG分别为两机励磁磁链的变化量。

联立公式(2)、(5)、(6)可将MGP功角ΔδMG的动态微分方程表示为

(7)

由公式(7)可知，功角ΔδMG的动态微分方程中包含ΔψfdM与ΔψfdG的微分形式，表明励磁磁链的变化会对MGP的功角产生影响。因此在对MGP建模时需考虑两套励磁系统的作用，将ΔψfdM和ΔψfdG作为状态变量，对应的线性化微分方程如公式(8)所示[18]：

(8)

式中：ΔEfdM和ΔEfdG分别为两机励磁电压的变化量，具有不同下标的系数L表示与电机参数有关的常数。

由此建立了以Δωr、ΔδMG、ΔψfdM、ΔψfdG为状态变量，以ΔTeM、ΔEfdM、ΔEfdG为输入变量的四阶MGP小干扰模型。

2.2 光伏采用MGP并网的小干扰模型

光伏并网系统的一般结构主要包括光伏组件、直流侧稳压电容、逆变器、滤波环节以及控制环节等。常用的八阶光伏并网小干扰模型可表示为[19]

(9)

式中：Δxpv为状态变量，Δupv为输入变量，S为外界光照强度，T为外界温度，Udc为直流侧电容电压，ugd、ugq、igd、igq分别为电网侧电压与电流d、q轴分量，ugcd、ugcq为逆变器出口侧电压d、q轴分量，Δx1、Δx2、Δx3为控制器内部状态变量。

在建立图2所示光伏通过MGP并网的小干扰模型时，需要充分考虑光伏系统与MGP系统的电气连接关系，主要体现在三个方面：

(1)光伏逆变器出口侧经滤波电感与同步电动机定子侧绕组相连，因此逆变器出口侧电流d、q轴分量igd、igq与同步电动机定子侧d、q轴输入电流imd、imq相等。

(10)

且MGP中同步电动机定子侧电流可用功角和磁链表示为如下形式[20]：

(11)

式中：系数m1M、m2M、n1M、n2M为与电动机初始条件有关的常数。

因此光伏直接并网小干扰模型中的状态变量Δigd、Δigq可用MGP小干扰模型中的状态变量ΔδMG与ΔψfdM替代。

(2)忽略滤波电感的有功功率损耗，则MGP同步电动机的电磁输入功率与光伏逆变器出口侧的有功功率相等，表示为公式(12)的形式：

ΔTpv=ΔTeM=ugcq0Δigq+igq0Δugoq

(12)

式中：ugcq0、igq0为逆变器端口侧q轴电压、电流初始值。

文中在控制策略上采用定q轴矢量控制，控制d轴电流为0，功率表达式中仅包含q轴分量。由公式(12)可知，MGP的输入变量ΔTeM可用光伏直接并网小干扰模型中的状态变量Δugcq与Δigq替代。

(3)光伏系统通过MGP并网后，转子转速与电网频率存在耦合，形式上表现为MGP转子频率ωr与电网角频率ωg相等。而原光伏系统中未将电网角频率考虑为状态变量，因此原状态矩阵中需增加以Δωr为状态变量的系数项。

综上，光伏经MGP并网后，原模型中的状态变量Δigd、Δigq被替代，系统阶数由八阶降为六阶，并与MGP四阶方程相联立，形成完整的光伏通过MGP并网的十阶小干扰模型如下：

(13)

式中：Δx为状态变量，Δu为输入变量，A为状态变量系数矩阵。

3 MGP抑制次同步振荡的特性分析

3.1 光伏采用MGP并网的小干扰模型

为分析MGP对光伏并网系统振荡模态的影响，文中通过算例对比同一控制器参数下光伏直接并网与通过MGP并网的小干扰模型特征模态。计算结果见表1，MGP算例结构与图2相同。

表1算例结果表明，光伏直接并网的小干扰模型存在4对特征模式。其中λ3,4=8.541±j60.963为一对不稳定极点，振荡频率为9.7 Hz。配置MGP后，系统增加了一组实部为负的特征值λ9、λ10，不会对系统稳定性造成影响。采用MGP并网方式后，由于同步电机的引入，系统中原有振荡模态λ3,4实部与虚部均减小。实部的降低反映了MGP可为光伏并网系统提供正阻尼，改善振荡情况；虚部的降低反映了振荡频率的减小，意味着MGP的引入将新能源电网的电磁振荡形式逐渐过渡为同步机的机电振荡形式。而对于同步机机电振荡的研究理论及抑制措施已经相对成熟，可在实际情况中加以借鉴。

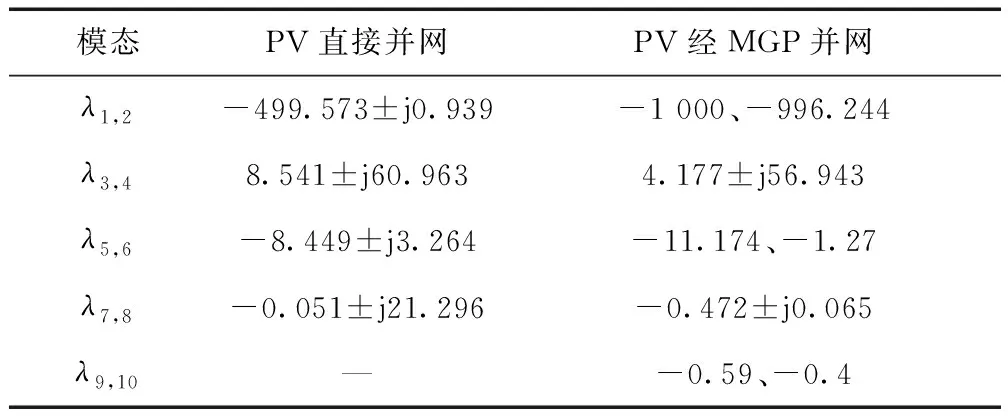
表1 不同并网方式下特征值计算结果Tab.1 The eigenvalues of different grid-connected system

3.2 控制器参数对不同并网方式下振荡模态的影响

对振荡模态λ3,4进行参与因子分析得知，主导参与状态变量为Δugcq与Δugcd。因此该振荡模态主要与控制器电压外环参数kp、ki，电流内环控制参数kpd、kid、kpq、kiq有关。控制器参数变化时，两种并网方式下次同步振荡模态λ3,4的根轨迹变化情况如图4所示。

以图4 (a)为例，光伏直接并网方式的初始运行点为9.355±j60.972；经MGP并网后，系统初始运行点校正至4.277±j56.82。再以图4 (c)为例，两种并网方式下的初始运行点相接近，但光伏直接并网方式下，内环控制器比例系数kpd、kpq需经8～9次调节才将不稳定极点校正至稳定区域；而经MGP并网后，控制器参数只经3～4次调节便将振荡模态校正至稳定区域。

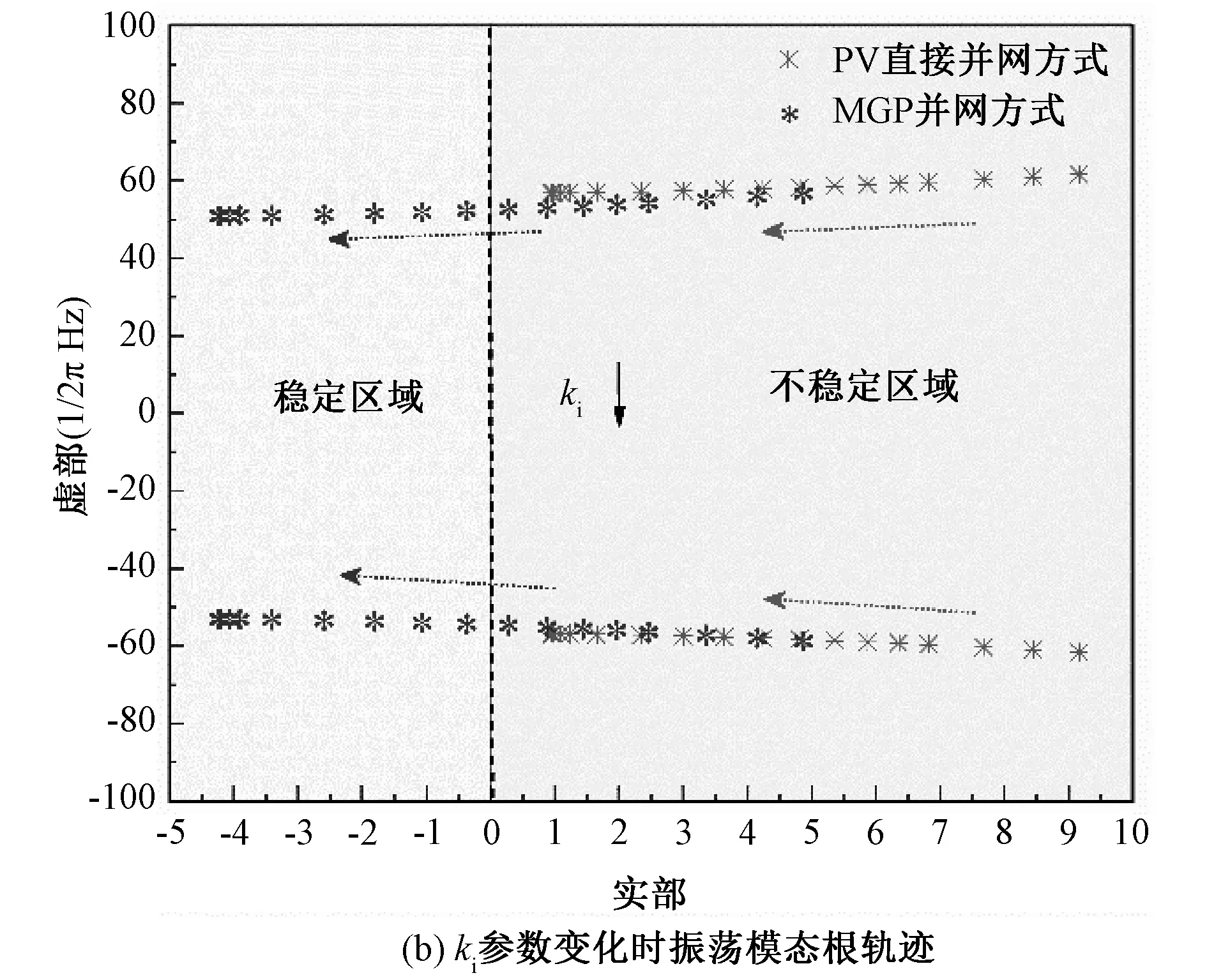
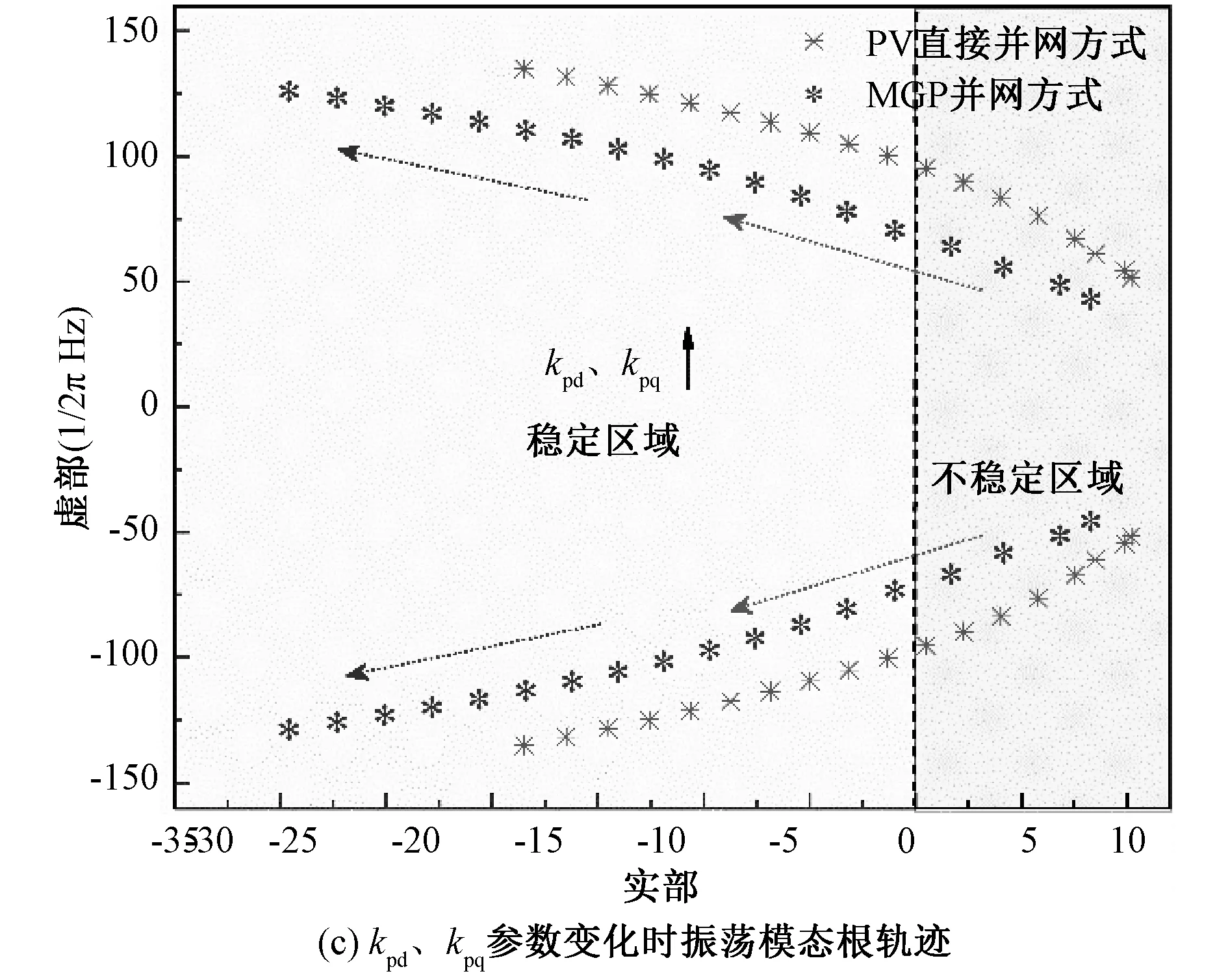
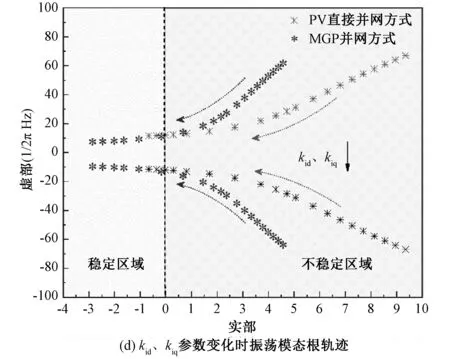
图4 控制器参数变化时振荡模态λ3,4根轨迹变化图Fig. 4 Root locus of mode λ3,4 as controller parameters changes

综合上述振荡模态λ3,4在控制器参数变化时的根轨迹可知，MGP对光伏系统振荡的改善效果主要体现在：1)光伏经MGP并网后，振荡模态的初始运行点相比于光伏直接并网方式更靠近虚轴，系统自身阻尼更强，初始稳定性更好；2)光伏经MGP并网后，振荡模态对控制器参数的响应更为灵敏，振荡模态能更快速的趋向于稳定区域；3)光伏经MGP并网可使得振荡形式从光伏系统的电磁振荡逐步过渡为以同步机为主的机电振荡，振荡危害更低，抑制理论更为成熟。

4 仿真验证

为验证上述光伏经MGP并网小干扰模型的准确性以及控制器参数在两种并网方式下对振荡模态的影响特性，文中基于图2结构在PSCAD仿真平台搭建了相应的仿真模型，系统参数参见表2。

表2 仿真系统初始值Tab.2 The initial value of simulation system

4.1 MGP并网与光伏直接并网小干扰稳定对比

大规模光伏电站一般建立在结构薄弱的内陆地区，需经过串补装置提高输电线路输电能力。因此分别在两种并网方式下于5 s时在输电线路中投入串联电容器补偿装置，有功功率及母线电压波形如图5所示。

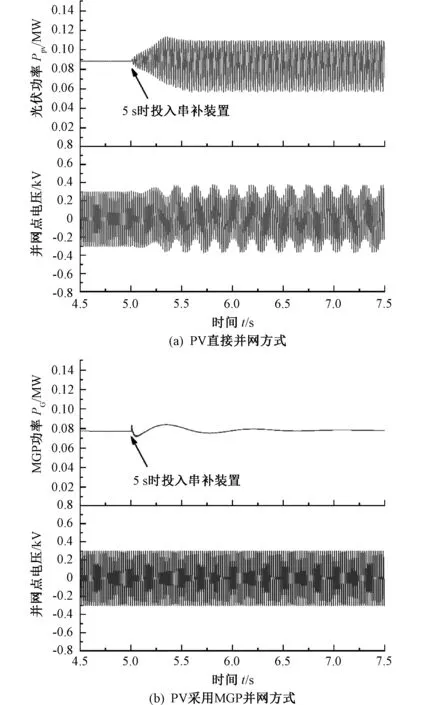
图5 两种并网方式下有功功率及母线电压Fig. 5 Active power and bus voltage under two grid-connected modes

图5中串联电容器补偿装置投入后，光伏直接并网系统有功功率与并网点电压均发生等幅振荡；而光伏通过MGP并网方式下，有功功率在2～3个周波后趋于稳定值78 kW，未出现明显的功率振荡，且并网点电压过渡平缓。

图6为两种并网方式下有功功率及并网点电压频谱分析结果。图6(a)光伏直接并网方式下有功功率中含有较高比例频率为45 Hz的次同步振荡分量，导致有功功率振荡发散。由于控制器的限幅作用，表现为等幅振荡，并网点母线电压中也存在与之对应的5 Hz次同步振荡频率。而图6(b)光伏经MGP并网后，有功功率中次同步振荡频率由45 Hz降低为2.27 Hz，谐波幅值也由0.02 MW降低为0.008 MW，振荡形式由电磁振荡过渡为机电振荡，系统阻尼得到加强，与理论分析相符合。

图6 功率及电压频谱分析图Fig. 6 Spectrum analysis of power and voltage

4.2 控制器比例系数对两种并网方式下振荡模态的影响

图7为控制器比例系数kp设置为0.5、1、1.5不同情况下，两种并网方式在串补装置投入时对应的有功功率。

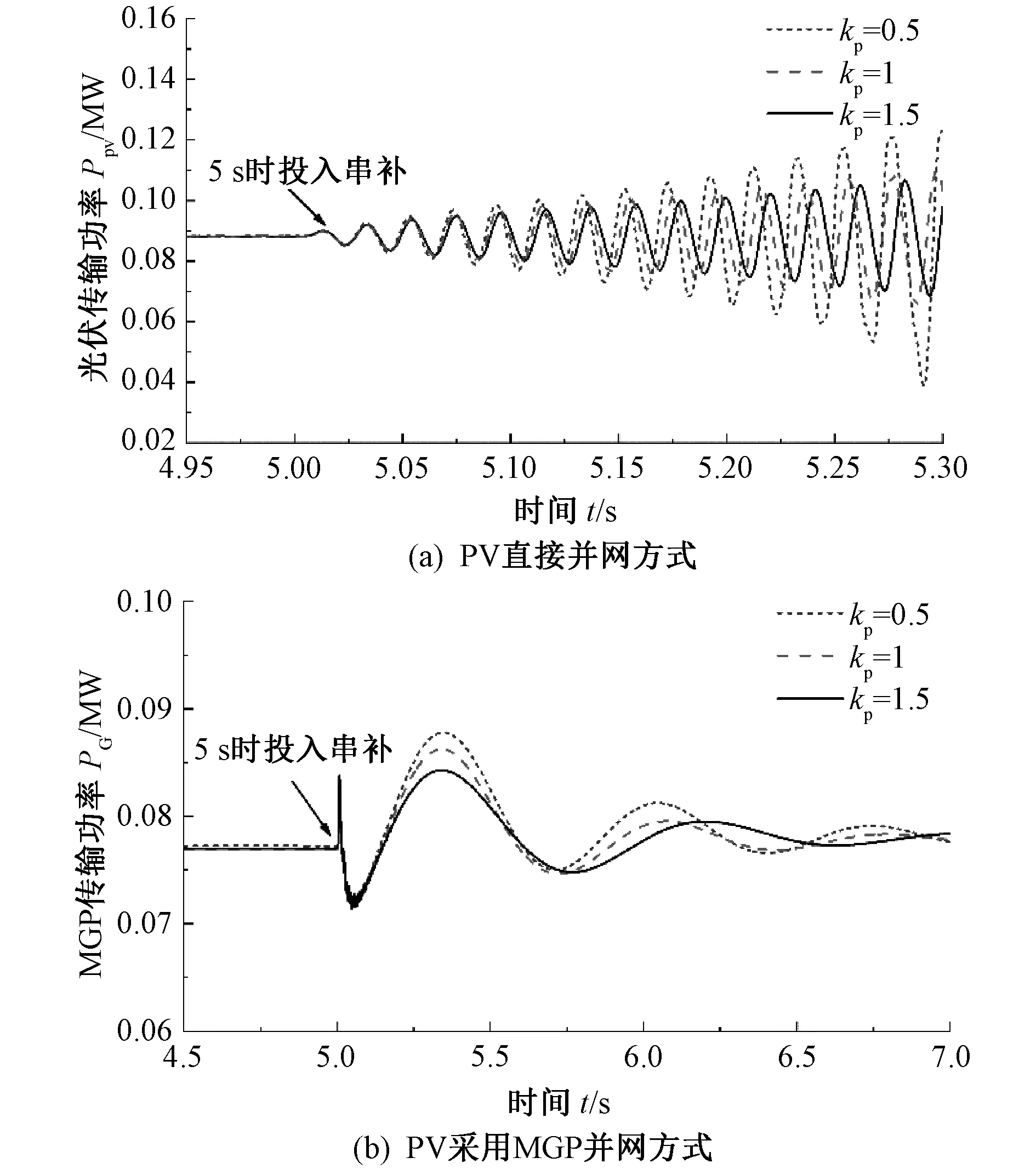
图7 不同kp参数两种并网方式下有功功率波形Fig. 7 Active power under two grid-connected modes with different kp

图7(a)中比例系数kp越大，光伏传输功率振荡幅度越小，振荡频率也越低，但光伏系统振荡模态并未衰减，系统不能稳定运行；图7(b)中MGP传输功率的振荡幅值与振荡频率也随比例系数kp的增大而减小，有功功率波动在3～5个周波内衰减，线路中未出现持续的次同步振荡现象，与根轨迹变化情况相符合。

4.3 控制器积分系数对两种并网方式下振荡模态的影响

图8为控制器外环积分系数ki设置为0.2、0.15、0.1不同情况下，两种并网方式在串补装置投入时对应的有功功率。

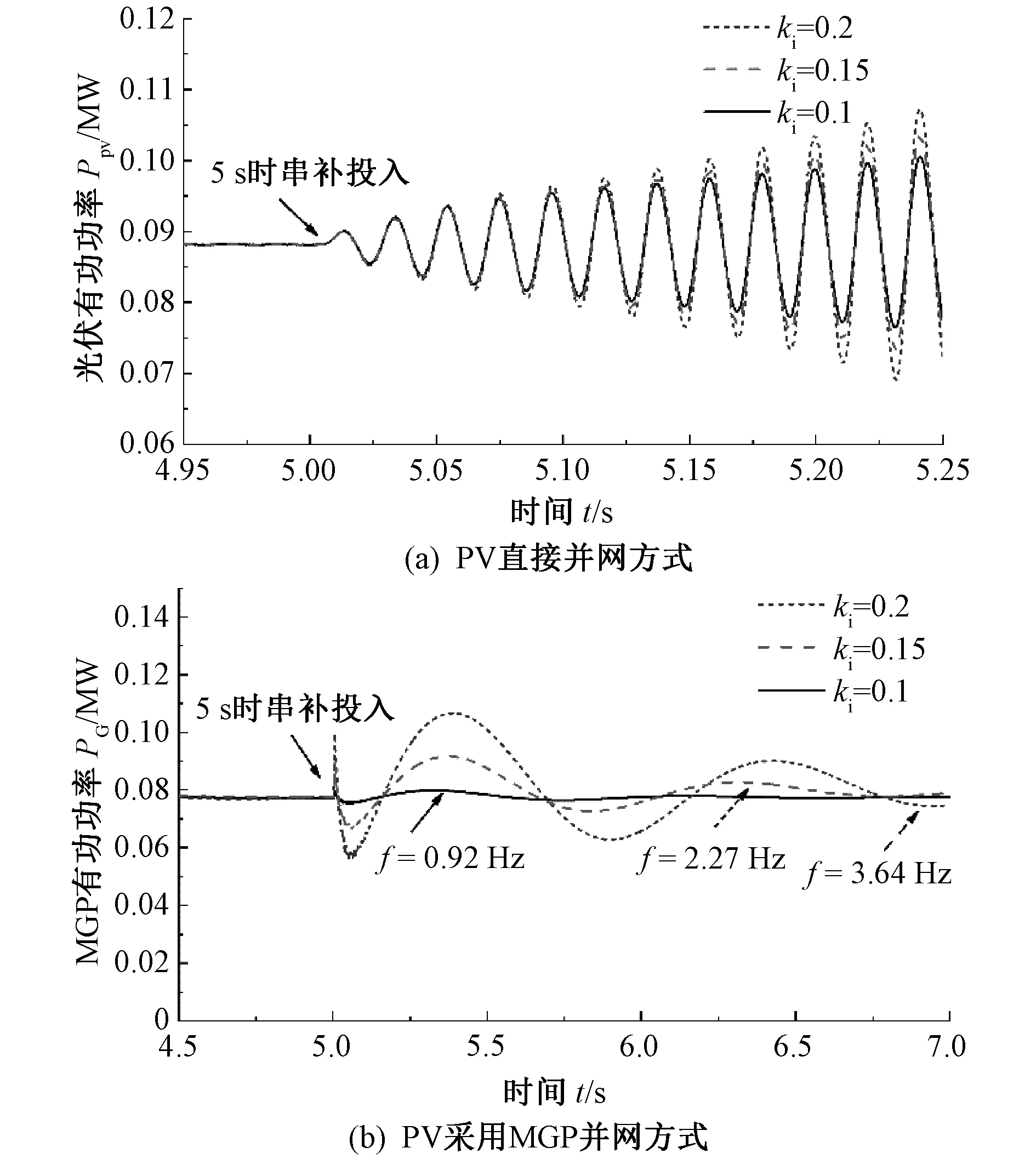
图8 不同ki参数两种并网方式下有功功率波形Fig. 8 Active power under two grid-connected modes with different ki

图8(a)光伏直接并网方式下，有功功率振荡幅值随控制器积分系数ki的减小而降低，但振荡幅值仅改善了0.003 MW，振荡幅值与振荡频率变化均不明显，系统依然存在振荡模态。图8(b)光伏经MGP并网方式下，有功功率振荡幅值降低了0.028 MW，振荡频率也由3.64 Hz减小为0.92 Hz，振荡改善效果更为明显。因此MGP对控制器参数的响应更为灵敏，与根轨迹分析一致。

4.4 电网强度对两种并网方式下振荡模态的影响

电网强度可用短路比(short circuit ratio，SCR)来衡量。有研究表明电网强度也是引起新能源电网次同步振荡的重要因素[21，22]。特别在弱电网条件下，次同步振荡的风险更为严重。而MGP的并网方式可凭借同步机的强励磁特性，为电网提供强度支撑。

图9为仿真系统稳定运行时，电网强度由SCR=5分别降低至SCR=2.5、SCR=2、SCR=1.5三种情况下，两种不同并网方式对应的有功功率响应曲线。

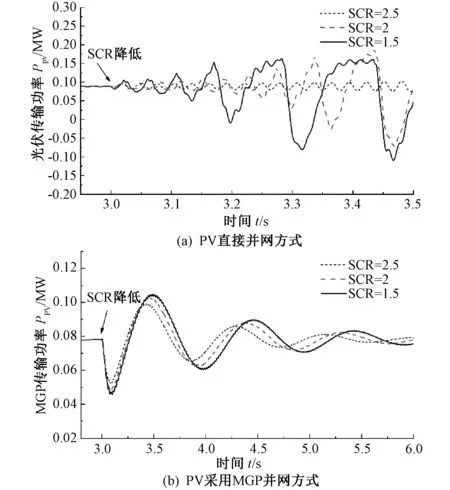
图9 不同电网强度下两种并网方式下有功功率波形Fig. 9 Active power under two grid-connected modes with different SCR

图9(a)光伏直接并网方式下，有功功率在SCR降低后出现振荡，振荡幅值随SCR的降低而增加，线路中有持续的次同步分量。图9(b)光伏经MGP并网方式下，MGP有功功率在电网强度降低时未出现持续的振荡现象。即使在弱电网(SCR=1.5)情况下，有功功率仍能在3～4个振荡周波内趋于稳定，体现了MGP对新能源电网强度的支撑作用。