高弹性电网下考虑不确定性的负荷调控两阶段优化模型

盛建雄， 张云峰， 叶 韵， 虞思城， 黄绍模， 孙 毅， 李泽坤

(1.国网浙江省电力有限公司湖州供电公司， 浙江 湖州 313000；2.华北电力大学电气与电子工程学院，北京 102206)

0 引 言

针对源荷缺乏互动、平衡能力缩水等问题，浙江电网首次提出构建能源互联网形态下的多元融合高弹性电网，推动源网荷储柔性互动，提升需求侧海量资源聚合和协调控制能力，实现电网的资源优化配置[1，2]。其中，需求侧海量柔性负荷是提高电网弹性的关键调节资源，是高弹性电网建设的重要组成部分[3]。

电网弹性定义为在面对供需平衡的大幅波动和电网故障时，电网资源弹性互动和灵活响应能力[4]。应对电网供需不平衡时，需求侧柔性负荷表现出十分可观的调节潜力。通过源网荷储友好互动，电网通过分时电价、电价补贴等激励方式，调整用户用电模式，转移用电高峰/低谷，深度挖掘用户侧资源可调潜力，获取更大的调节和控制空间，精准响应电网需求，进而维持电网供需平衡和稳定运行，提升电网弹性。

用户作为负荷的调控主体，其行为的不确定性会对电网的调控效果产生一定的影响。以浙江电网为例，2020年省外来电和新能源发电大幅提升，最大外来电力超过2 800万kW，新能源发电装机达1 731万kW，电网调节能力持续下降，弹性需求越来越大，此时海量的需求侧可控资源成为提高新能源消纳率、提高电网弹性和稳定性的一大助力[5]。但实际上用户行为具有较大的不确定性，尤其是价格不敏感型用户，在仍有控制权的基础上很大程度会降低电网预估的可调弹性空间，响应电网需求精准性不足，导致电网运行调度出现偏差[6]。为了降低不确定性对电网供需平衡的波动影响，精准响应电网需求，进一步提高电网弹性，本文以使用普及率高、数量巨大且储能性能优良的电热水器为例[7]，深入研究了考虑不确定性的负荷调控优化模型。

目前已有较多针对电热水器调控策略的研究。文献[8]利用电热水器进行风电消纳，提出一种实时控制电热水器负荷群的滑模控制策略，但该策略仅利用负荷群体的特性进行调控，并没有考虑电热水器调控中用户的用电需求及行为；文献[9-10]则对电热水器的相关参数进行聚类分析，进而调用电热水器负荷群参与电网的低频减载，在电热水器完全受控的前提条件下取得了优于传统调频方式的效果，并未考虑用户不确定性行为的影响；文献[11]为实现不同负荷的交叉式调控，基于用户满意度对电热水器与空调进行归一化分析，构建电热水器与空调的满意度模糊集合，确定负荷的调控顺序，但其定义的满意度根据负荷温度设定，缺乏对异构负荷之间调控误差的考虑[12]；文献[13]则建立一种分析用户用电行为的模型，提取用户用电特征，未深入分析用户行为的不确定性。上述研究的调控策略在确定性场景下均能取得良好的调控效果，但未考虑用户不确定性行为等因素对负荷调控造成的影响。

为了使负荷调控策略在实际中提供更多指导价值，已有较多关于负荷调控策略的研究考虑了用户不确定性行为的影响。文献[14]通过采用鲁棒优化方法处理响应过程的不确定性，减少了居民行为不确定性的影响；文献[6]则从消费者心理学原理角度，在价格型与激励型需求响应下分析用户响应行为的不确定性，找出所引起需求响应不确定性的偏差变化规律，建立考虑响应不确定性的调控模型，实现了调控效果的优化；文献[15]通过分析电动汽车用户的实际调查数据，得出荷电状态呈现出均匀分布的特征，进而基于该典型的分布特征实现对用户行为随机性的建模。上述研究为研究负荷调控中用户行为的不确定性提供了良好的参考，但并未深入分析用户不确定性行为的特点及其对负荷调控影响的机制，难以进一步对构建的不确定性模型优化调整。

针对以上研究缺乏考虑或未能深入分析用户不确定性行为的不足，本文在已有的研究基础上，综合考虑负荷预测误差与用户不确定性行为的影响，基于历史数据构建具有概率约束的不确定集，进而提出基于概率约束不确定集的两阶段优化模型，降低负荷调控中的不确定性影响，提高电网可调弹性空间。本文的创新在于利用基于概率约束的不确定集对负荷调控中的用户行为不确定性进行精细化研究，更为全面地分析用户行为不确定性造成的影响，与其余研究相比，本文的不同之处如表1所示。

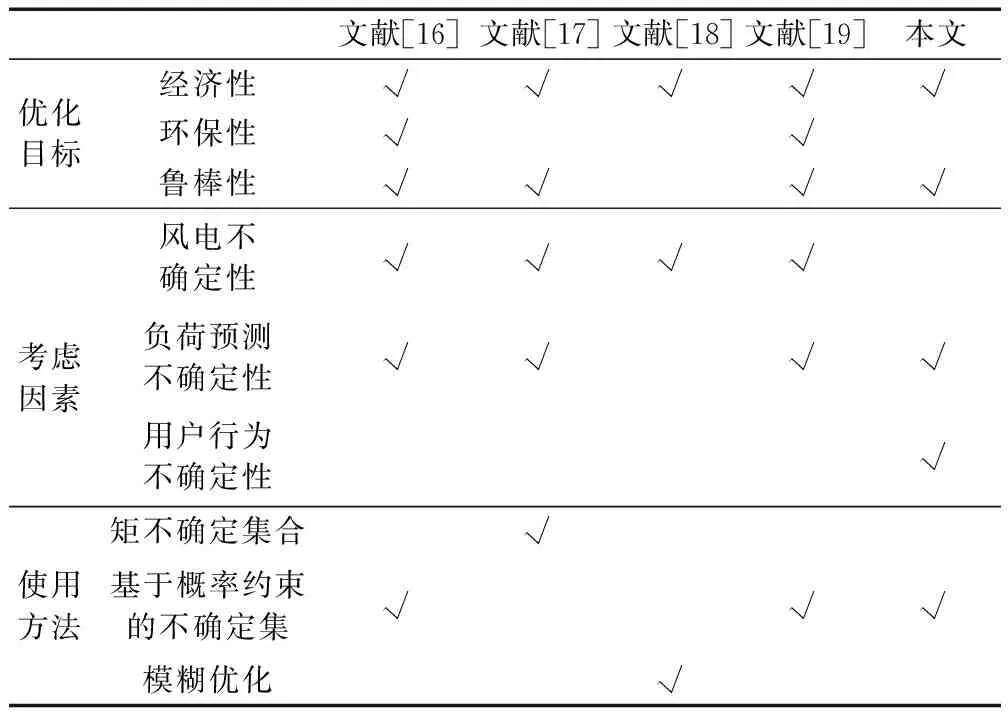
表1 本文与其他文献的对比Tab.1 Comparison of this article with other documents

1 负荷实际调控过程及不确定性分析

1.1 面向高弹性电网的负荷实际调控过程分析

随着分布式能源、储能电站的高比例接入，电网自身接纳能力有限，为应对新能源发电的随机性和间歇性，需求侧负荷资源便成为了提高电网弹性、降低弃风弃光的重要手段。本文以电热水器消纳风电为例，采用签订实时合同机制[20]，说明电热水器参与消纳过程中存在的不确定性。基于合同机制，本文电热水器消纳风电过程可分为信息采集、功率预测、签订合同、负荷聚合、调控实施5部分，如图1所示。

图1 负荷调控过程Fig. 1 Load regulation process

在合同机制下，通常认为可忽略负荷调控中用户不确定性行为的影响[21]。但在实际中因外界因素影响，聚合商并不能全部调度所有签订合同的用户负荷，仍会有部分控制权转移回到用户中，如图1所示。因此，在假设用户在负荷调控中仍具有负荷控制权的基础上，分析负荷预测误差与用户不确定性行为对负荷调控过程的不确定性影响。

电热水器负荷参与调控的过程如下：聚合商收到新能源出力信息后，需要一定的时间完成调控电热水器消纳风电的过程。由于数学模型匹配不精准、负荷数据失真、外界随机性干扰[22]等因素的影响，预测技术难以完全消除预测误差，即在功率预测步骤中已存在偏差。同时，在功率预测与负荷聚合的时间间隔内，负荷状态等信息仍会发生变化，聚合商在负荷聚合步骤中根据功率预测结果进行负荷聚合，导致聚合的负荷群不能完全满足实际的负荷调控需求，出现第一阶段偏差。负荷群完成聚合后，进入调控实施步骤，该步骤中存在用户不确定性行为的影响，即出现用户负荷中途退出消纳或中途加入消纳的违约行为，导致调控实施出现第二阶段偏差。综上，负荷调控中不确定性的影响可如图2描述。从图中可知，在风电出力功率不变的条件下，两阶段偏差的影响使得负荷群的实际聚合功率已偏离预期，较难达到预期的消纳效果和电网预估的弹性可调容量。

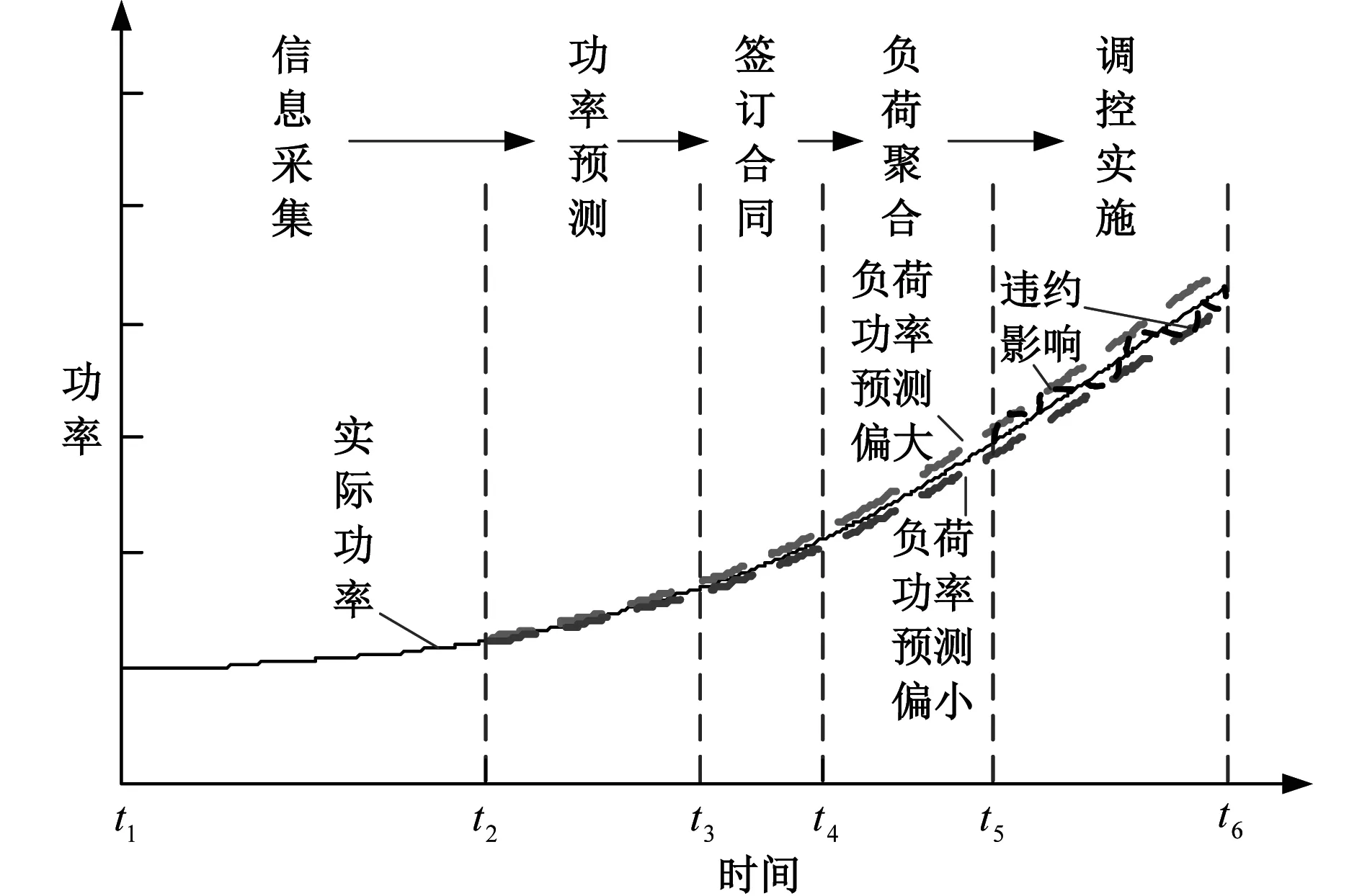
图2 负荷调控中不确定性造成的偏差Fig. 2 Deviation caused by uncertainty in load regulation

本文选用等效热参数模型(ETP)描述仿真实验中单台电热水器负荷的运行状态，ETP模型如下：

s(t)PR]

(1)

式中：T(t)、T0(t)、s(t)分别为t时刻的温控负荷温度、环境温度、开关状态，P为负荷额定功率，R为热阻，C为比热容。基于此模型的仿真实验中，电热水器可模拟负荷聚合过程，在聚合过程中存在不确定性的影响，对t时刻负荷聚合功率Pt,s而言，该影响可用式(2)描述：

(2)

式中：Pi为负荷i的额定功率；N为负荷数量；ω′与ω均为不确定性变量，分别引起负荷调控中的第一阶段偏差与第二阶段偏差，将使用下节基于概率约束的不确定集方法进行数学描述。

1.2 基于概率约束的不确定性因素描述

1.2.1 基于数据的不确定集构建方法

通常，不确定集具有参数等权重的特点，包含了发生可能性很低的情况，增加了不确定性问题的求解成本。因此，本文利用历史数据侯建基于概率约束的不确定集，使不确定集的描述更贴近实际情况。考虑到智能电表等监测工具的周期性采集，历史数据一般为离散性数据，因而表示负荷调控中负荷预测误差与用户行为的不确定性的不确定变量具有离散性。本文使用的历史数据可分为两类：用户历史用电行为及负荷预测数据，这两类历史数据包含的信息如表2所示。

表2 离散性历史数据中的信息Tab.2 Information in discrete historical data

下面将通过历史数据寻找两个变量的概率分布，构建基于概率约束的不确定集。假设S={α1α2…αm}为按数值大小升序排列的历史数据集，且αi∈S，则基于S数据集可得到αi的经验分布记为ψ(αi)，如下所示。

(3)

αi的经验分布函数为

(4)

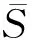
(5)

(6)

(7)

选取与样本均值绝对值差值最小的上限或下限作为不确定集的最终上下界限，保证盒式不确定集的对称性。综上，使用历史数据得到基于概率分布不确定集如下式。式中，αk(ε)、αl(ε)分别是显著性水平为ε时不确定集的下界与上界，Pr表示显著性水平为ε时αi在αk(ε)≤αi≤αl(ε)区间内的概率为1-ε。

(8)

1.2.2 负荷调控的不确定性因素描述

基于前述分析，负荷调控的不确定性包括负荷预测误差与用户行为的不确定性，前者出现在实施负荷调控前，后者在实施负荷调控过程中出现。下面使用1.2.1节的方法描述这两阶段的不确定性。

(1)负荷调控前的不确定性描述

基于各时刻负荷聚合功率的实际历史数据，可以得到负荷预测技术在各时刻的预测误差，按下式计算。

σt=Pt,pro-Pt,act

(9)

式中：Pt,pro为t时刻的负荷聚合功率预测值；Pt,act为t时刻的负荷聚合功率实际值，σt为t时刻负荷聚合功率预测值与实际值之间的误差。在同一场景下，负荷的预测误差较为稳定，其波动范围有限[24]，则有ω′∈{σ1,σ2,…,σm}。对于同一负荷预测技术而言，ω′可用一个不确定性的区间来描述，且呈现出一定的分布特点。基于1.2.1节的不确定集构建方法，在置信水平为1-ε时，ω′的不确定集Uω′如下所示。

(10)

(2)负荷调控中的不确定性描述

通过对比合同计划调控时间与用户实际参与调控时间，可从历史数据中判定用户违约行为。以不确定变量ω表示用户的违约行为，以上述对比调控时间的判定方法，得到用户的整体违约情况，则ω的取值空间{β1,β2,…,βm}。根据1.2.1节的方法，假设用户违约行为服从如下分布。

(11)

则在置信水平1-ε下用户违约行为的不确定集Uω为

(12)

2 考虑不确定性因素的负荷调控优化模型及求解

2.1 多目标两阶段优化模型构建

本文以负荷调控的稳定性与经济性为优化目标，提出了两阶段优化思路，具体为：下层问题考虑负荷预测误差带来的不确定性，构造负荷聚合功率与新能源出力功率差值最小的目标函数；基于下层目标函数的优化结果，上层问题关注负荷调度的经济性，以最小化负荷聚合商的调度成本为目标。

(1)在上层经济性问题中，聚合商调度的成本包括两方面：负荷预测后进行购电的成本及调控中用户违约行为造成的成本。在下层鲁棒优化决策结果的基础上，该层在目标函数式(13)的引导下对负荷调控进行优化，使聚合商的调度成本最小，目标函数如下：

(13)

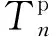
上层目标函数考虑交易价格、调控时间等方面的约束，具体如下：

(14)

(15)

(2)下层问题以最小化负荷聚合功率与出力功率之间的差值为目标。在负荷参与调度的过程中，负荷预测调度值与实际调度值之间存在误差，若该误差较大，按照负荷预测调度值制定调度方案可能造成电网的运行安全。在调控时段Nt内，聚合商要尽可能减小t时刻负荷聚合功率Pt,s与聚合商购电总功率Pt,b之间的差值，其线性优化目标一般为

(16)

在考虑负荷预测误差的不确定性影响后，目标函数应为下式所示。

(17)

下层目标函数较多涉及了负荷的运行过程，其约束条件应包括如下几方面。

(1)任意t时刻功率平衡约束：

Pt,G+Pt,b=(1+τ)Pt,s

(18)

式中：Pt,G为常规机组t时刻的出力，τ∈ξ，表示负荷的预测误差，为不确定变量。

(2)聚合商购电总功率与新能源预测出力功率Pt,p、新能源电站最大功率Pn,max应满足如下约束：

Pt,b≤Pt,p≤Pn,max

(19)

(3)聚合商所能调度的负荷资源存在上限，任意t时刻的调控功率不能超出所有合同用户负荷的总功率Pu,max，如下：

0≤Pt,s≤Pu,max

(20)

2.2 模型求解

本节针对包含不确定集的两阶段优化模型进行求解。对于目标函数中的不确定集，在置信度1-ε下，将模型中的不确定变量转换为最“劣”情况下的线性约束条件，从而对模型进行求解。

针对上层目标函数的成本优化，在调控过程中或会出现退出调控的负荷数量最多，同时用户中途加入调控的负荷数量最多的情况。从负荷整体运行角度分析，在退出调控与加入调控的负荷总功率相差较小时，这种情况不会造成严重的功率平衡问题。因此，该情况会增加聚合商的调度成本，是成本优化调控的最“劣”情况。该情况下，上层目标函数及式(15)的约束可以改为如下形式：

(21)

(22)

对于下层目标函数，当负荷预测误差达到负值最大或正值最大时，将对应负荷鲁棒优化调度的最“劣”情况。当负荷预测误差达到负值最大时，可以将下层目标函数与式(20)的约束改写为如下形式：

(23)

0≤(1+σi(ε))Pt,s

(24)

当负荷预测误差达到正值最大时，下层目标函数与式(20)的约束改写为如下形式：

(25)

(1+σj(ε))Pt,s≤Pu,max

(26)

通过上述步骤，将不确定变量转换成了线性约束条件，在上层变量Pt,b给定的条件下，下层问题的拉格朗日函数可表示为式(27)、(28)，分别对应下层问题的两种最“劣”情况。

(27)

(28)

式中：μ1,n、μ2,n、μ3,n、μ4,n与λ1,n、λ2,n、λ3,n、λ4,n分别为对应式(27)与式(28)约束的拉格朗日乘子。以下层问题中预测误差负值最大的情况为例，式(27)的KKT条件如下：

(29)

(30)

μ1,n≥0

(31)

μ2,n≥0

(32)

μ3,n≥0

(33)

μ4,n≥0

(34)

μ2,n(Pt,p-Pt,b)=0

(35)

μ3,n(Pn,max-Pt,p)=0

(36)

通过将下层问题用KKT条件替代，从而将两阶段优化模型转化为单层优化模型。其中，目标函数为式(21)，约束条件包括式(14)、(15)、(18)、(19)、式(24)及式(35)、(36)。式(35)、(36)为互补松弛条件，不能直接采用混合整数规划算法进行求解。本文参考文献[25]的方法，引入一个充分大的常数M与0-1辅助变量ωn、ω′n将互补松弛条件转为(37)～(40)的不等式约束。

μ2,n≤Mωn

(37)

Pt,p-Pt,b≤M(1-ωn)

(38)

μ3,n≤Mω′n

(39)

Pn,max-Pt,p≤M(1-ω′n)

(40)

经过转换后的单层优化模型为一个混合整数线性规划模型，使用yalmip软件包进行求解。

3 算例分析

3.1 仿真设置

电热水器在一天中部分时段内大量集中使用[23]，根据文献[7]对电热水器的调控研究，本文的仿真时间设在电热水器的集中使用时段，仿真时长设为4小时，热水器负荷的数量为3 000台，目标调控曲线参考文献[23]。相关物理属性参数如表3所示，表中购电电价基于文献[26]的数据利用插值法进行设置，额外成本电价为购电电价的2～3倍。

表3 参数设置Tab.3 Parameter settings

3.2 仿真分析

(1)不确定性影响下的负荷调控效果分析

为更好说明具体的不确定性因素对负荷调控的影响，首先在无用户行为不确定性影响的基础上进行仿真实验，得到其负荷消纳曲线。其次，考虑负荷预测误差与用户行为不确定性的影响，设置95%、90%、85%的置信度进行仿真，分别得到相应的负荷消纳曲线，并与目标消纳曲线对比，如图3所示。由图可看出，无用户行为不确定性影响的负荷消纳曲线与目标曲线存在一定的偏差，这是由于负荷预测误差造成的影响。而不同置信度下的负荷消纳曲线受到负荷预测误差与用户行为不确定性的影响，消纳效果较差。

图3 不确定性影响下的负荷调控效果Fig. 3 Control effect under different confidence levels

用户行为不确定性主要对电热水器的运行造成影响。如图4所示，在不确定性的影响下单台电热水器的开关会改变现有的状态，导致电热水器的温度运行状态改变，当被不确定性影响的电热水器数量多于一定数量后，最终对整体负荷调控效果造成影响。

图4 单台电热水器的状态变化Fig. 4 Status change of single electric water heater

根据前述分析，其中负荷预测误差只对调参与调控的电热水器数量有影响，不影响电热水器的运行状态，因而在调控实施过程中只存在用户行为的不确定性影响。为进一步分析用户行为不确定性的影响，在不同情况下分析其中60台电热水器的平均温度变化，如图5所示。由图可知，用户行为不确定性会造成电热水器的平均温度变低，且置信度越低，其造成的影响越大。

图5 用户行为不确定性对平均温度的影响Fig. 5 Impact of user behavior uncertainty on average temperature

为进一步分析负荷调控中不确定性的影响，对不同置信度下负荷消纳的功率偏差进行统计分析，因偏差值存在正负值，以绝对值的方式进行统计，如图6所示。从图中可看出，85%置信度下的总功率偏差最大，且置信度越低，功率偏差越大。为更好对比不同置信度造成的偏差程度，将总功率偏差与预期总负荷功率的比值定义为偏差率，根据图中的数据可计算得到85%、90%、95%置信度下的偏差率分别为15.2%、8.3%、4.6%，即置信度越高，不确定性造成的影响越弱。同时，在置信度相差为5%时，置信度从95%降为90%时偏差率变化小。综上，本文使用离散性历史数据构建基于概率约束的不确定集能够较为精准地描述负荷调控中的不确定性，从而降低不确定性的影响，有效整合需求侧负荷资源，精准匹配新能源发电和响应电网供需平衡需求，提高电网弹性。

图6 不同置信度下的功率偏差Fig. 6 Power deviation under different confidence levels

(2)不确定性影响下的调度成本分析

为进一步分析不确定性对负荷调控的成本影响，可从不确定性造成负荷调控的功率偏差，从而导致聚合商需承担额外调度成本的角度分析，该成本可根据式(13)与仿真结果计算得到，如表4所示。

表4 不同消纳情况的结果对比Tab.4 Comparison of results of different consumption situations

由表4可知，额外调度成本与置信度并不是线性关系，置信度为90%时负荷消纳的额外调度成本最低，这是用户行为不确定性造成的。根据式(13)，用户违约行为造成的额外调度成本由违约时长决定，违约时长越短则额外调度成本越低，在90%置信度下不确定集能更精准地描述用户行为的不确定性，使得用户整体违约行为与负荷预测误差造成的功率偏差相抵消，在实际中避免了过匹配或欠匹配的问题，最终导致负荷调控受到的影响最低，无须为用户行为不确定性的影响付出更多额外调度成本，因此90%置信度下负荷消纳的额外调度成本最低。同时，结合置信度改变造成的偏差率变化程度分析，在置信度为90%时，负荷调控可取得额外调度成本与偏差率相对较好的整体最优效果。

综合以上分析，通过设置合适的置信度，本文的两阶段优化模型可降低负荷调控中的不确定性影响。对于指定的用户群体，由于不同用户用电行为习惯的结果而表现出一定的用电特征[27]，在一定的较长时间内该特征都可视为此用户群体的一种固有属性，包括在负荷调控中表现出的不确定性，因此不同用户群体的合适置信度不易改变。对本文仿真实验中的负荷群而言，在多天内同一时段的合适置信度相似，负荷调控结果不会出现很大的差异。因用户群体的用电特征较为稳定，本文所提模型同样适用于不同的负荷调控场景，通过多次试验等方式找出属于不同场景下的合适置信度，实现降低不确定性影响的效果。

4 结 论

需求侧负荷资源的汇聚整合和协调控制是高弹性电网建设的重点内容之一。而不确定性作为影响负荷调控效果、降低电网弹性的重要因素，有必要对其进行过程分析和描述，进而完善调控模型，消除由不确定性带来的偏差。为降低需求侧不确定性对电网调度造成的影响，精准响应电网需求，进一步提高电网弹性和稳定性，本文分析了合同方式下不确定性对负荷调控的影响，基于离散性历史数据在一定置信度下构建基于概率约束的不确定集，并以此为基础，建立以负荷调控的鲁棒性与经济性为优化目标的两阶段优化模型，通过仿真实验分析了不确定性对负荷调控的影响，验证了本文构建的模型能够有效降低不确定性造成的影响，实现负荷额外调控成本与功率偏差率整体效果最优，有效响应电网需求，提高电网弹性。得出以下结论：

(1)基于概率约束的不确定集能很好描述负荷调控中的不确定性，且仿真结果表明，通过设置不同的置信度可降低不确定性造成的影响；

(2)在合适的置信度下，使用历史数据构建基于概率约束不确定集的两阶段优化模型有助于找出负荷调控效果与成本的“平衡点”，在不确定性影响下取得整体负荷调控的最优效果。

而如何利用深度学习，结合传统模型提高描述不确定性的精度，进一步降低不确定性对负荷调控的影响，是后续研究的方向之一。