微网系统电源动态特性差异导致的交互振荡与稳定性控制方法
2022-02-18郑凯元王海风
郑凯元, 王海风,2
(1.新能源电力系统国家重点实验室 (华北电力大学),北京 102206;2.四川大学 电气工程学院,四川 成都 610064)
0 引 言
微电网系统通过整合分布式电源(Distributed Generators, DGs)、储能、负荷与能量转换等装置,形成一个具备自我控制能力的自治系统[1],凭借其灵活高效和供电可靠等优势[2]在近些年得到快速的发展。微电网的控制设计和稳定性分析是微网研究的重要内容[3],其控制策略的目标是为了实现恰当的功率分配并维持孤岛运行状态下微网电压和频率的稳定[4],当前低成本/高效率的下垂控制[5]是微网系统较成熟和常用的控制策略。
微网由于电力电子化程度高、惯性缺失[6]等特性,更易受扰动而失稳,因此一个良好设计的微网系统必须是小干扰稳定性的[7]。影响微电网小干扰稳定性的因素主要包含(1)微型电源导致的交互作用,(2)电源-负荷间交互作用,(3)多微网或交直流微网互联和(4)运行点改变和通信延迟等因素。在并网运行状态下,微电网的稳定性问题主要是单个电源/负荷的影响[8],稳定性分析主要针对孤网运行状态的微网系统。
通常微网中DGs可通过电力电子换流器或旋转机械[9]接入微网,逆变器类(inverter-based DG, IBDG)分布式电源对控制的响应迅速、但也容易受到扰动发生振荡;同步机类(synchronous-based DG, SBDG)电源包含同步电机及励磁和速度控制器,具有一定的惯性。微网系统中多种动态特性不同的微源共存、电气距离较近会导致电源间耦合交互[10]从而恶化微网稳定性,引发低频/高频振荡、IBDG过载等问题。下垂控制间交互作用导致低频失稳[11]是微网稳定分析中的一个核心问题:文献[12,13]分析并联IBDGs间交互振荡对微网低频动态的影响,指出功率下垂系数不当会导致微网低频振荡失稳;文献[14]研究基于角度下垂控制的负荷分配策略,发现弱电网条件下功率精准分配需要的下垂参数可能导致低频振荡;文献[15]指出低频范围模式主要受到逆变器功率分配/控制环节的影响、高频范围振荡模式主要受到逆变器电压-电流控制环节的影响;不同IBDGs电压控制环节间的耦合[16]会导致中频率范围的失稳,而下垂系数过大导致IBDG功率控制环与电压控制环的耦合会引发低频振荡、电压控制环与电流控制环带宽接近[17]会导致高频振荡;文献[18]讨论在多微网系统(Multi-microgrid, MMG)中存在的IBDGs间交互振荡、以及线路拓扑和参数的影响;此外电网跟踪型IBDG锁相环引入q轴负阻效应[19]也可能导致系统失稳。
针对微源动态特性不同的情况,文献[20]注意到慢动态响应的柴油机和快动态响应IBDG间动态交互导致低频失稳的情况;文献[21]研究了下垂参数对含SBDG/IBDG微网稳定性的影响;文献[22]研究了IBDG和SBDG间负荷均流特性差异导致的微网系统失稳;文献[23]指出微网系统的低惯性特性和复杂控制算法会致模式强交互作用,研究了IBDG和SBDG间强动态交互作用导致的低频失稳;光伏电源与水电机组[24]、不同结构的下垂控制型逆变器类电源之间[25]存在的交互作用均可能导致机组间振荡;文献[26]针对含IBDG和SBDG的多微网系统,分析了系统结构和参数对低频交互主导振荡模式的影响;文献[27]通过过将混联微网根据动态特性的快慢拆解为两个子系统,证明具有快速动态特性的换流器与较慢动态特性的机电振荡单元间交互作用引起会引起混联系统失稳。
此外,IBDG逆变器端口LCL滤波器[28]在欠阻尼情况诱发高频谐振,微源与动态负荷间[29]交互作用、系统运行点[30]变化、通信延迟[31]的不当取值均可能导致微网系统失稳。基于上述文献回顾可发现,关于微源动态特性差异导致失稳的研究不够深入,多基于特征值/阻抗分析法讨论特定参数对振荡阻尼/稳定裕度的影响[32]。相应稳定性增强措施包括额外阻尼控制[26,33]、虚拟阻抗下垂[34]控制,和引入功率积分[35,36]或超前/滞后补偿器[37]或者直流电容电压反馈[4]以改进下垂控制,对抑制由于电源动态特性不同导致的振荡失稳针对性较弱。
本文建立了包含SBDG和IBDG的微网状态空间模型,首先基于降阶的方法、定性的分析了不同类型电源动态特性差异如何影响电源间的交互振荡;其次,基于特征值分析的方法,探究了微网中关键参数对振荡模式的影响;然后,提出一种相角锁定控制策略,以抑制电源动态特性差异导致的低频振荡;最后,通过微网系统和多微网系统算例,验证文章分析的正确性与所提控制方案的有效性。
1 微网模型建立

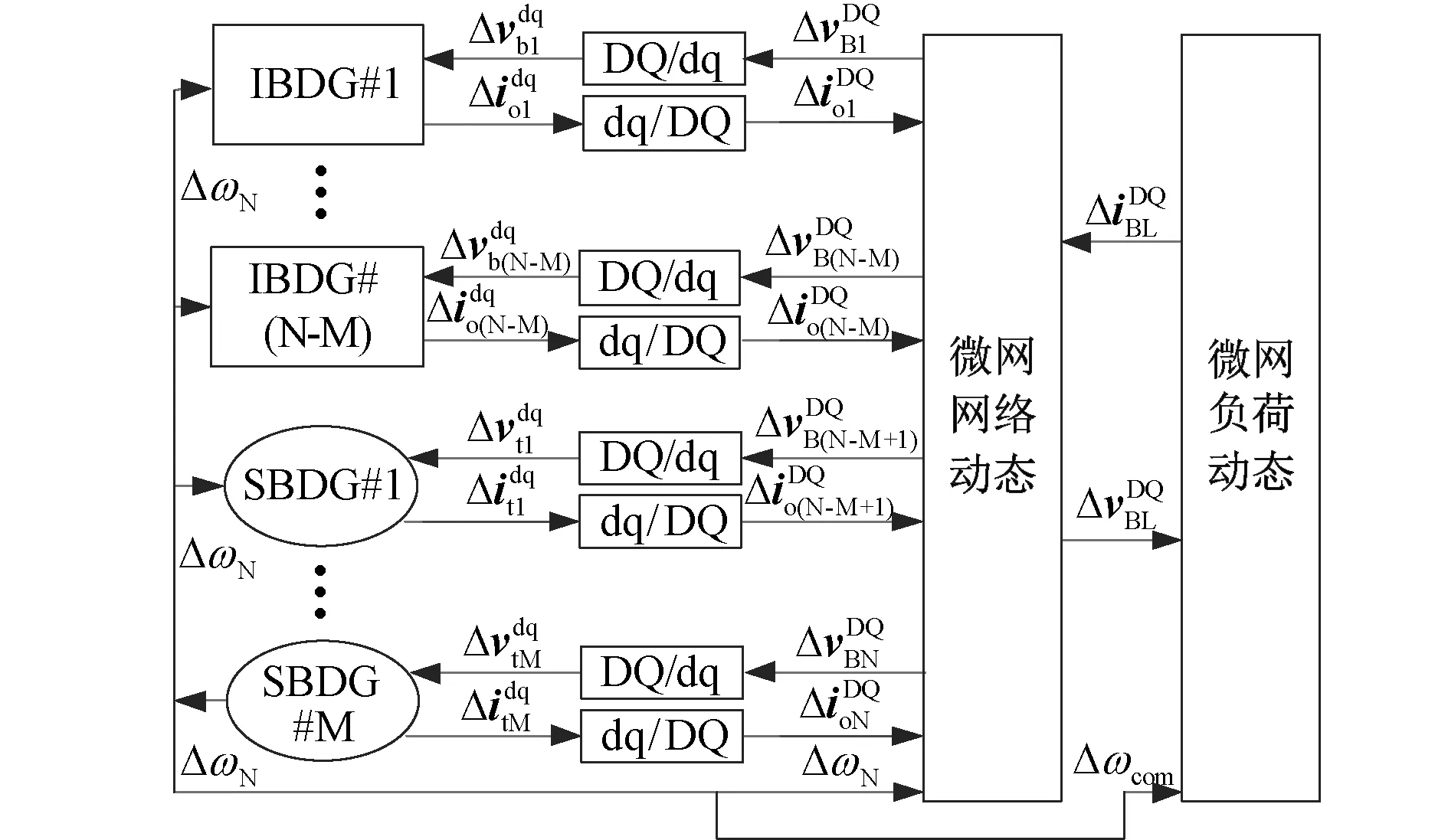
图1 含多DGs电源的微网系统小信号状态空间示意图Fig. 1 Block diagram of complete small-signal state-space model of a microgrid with multiple DGs
本文讨论含IBDG和SBDG两种电源的微网系统稳定性,详细建模过程如下。
1.1 逆变器型分布式电源IBDG
图2所示IBDG动态包含四部分:(1)逆变器端口电压电流;(2)功率下垂控制;(3)逆变器电压控制外环和(4)电流控制内环。

图2 IBDG电源下垂控制Fig. 2 Dynamic droop controller for IBDG
端口滤波电流[ildilq]T,滤波电容电压[vodvoq]T和线路电感电流[iodioq]T的动态关系如式(1a)所示,换流器输出有功/无功功率如式(1b)所示。Lf和Cf为滤波电感和电容,vcd和vcq为逆变器端口电压,RL和LL为线路电阻和电感,ω为逆变器坐标系角速度,[vbdvbq]T为端口电压。
(1a)
p=vodiod+voqioq;q=voqiod-vodioq
(1b)
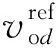
(2)
式中:ωc为滤波器截断频率;mp和nq分别为有功和无功下垂系数;ωn和Vn分别为角速度和电压参考值;ωcom为微网参考/公共坐标轴角速度。
(3)
式中:xud和xuq为外环积分环节输出,F为电流反馈系数,kup和kui为电压外环比例和积分系数。
(4)
式中:和xid和xiq为内环积分环节输出,kip和kii为PI控制比例和积分系数。将式(1)~(4)线性化可得IBDG的状态空间模型
sΔXIBDG=AIΔXIBDG+BIV[ΔvbdΔvbq]T+BIωΔωcom
[ΔiodΔioq]T=CIΔXIBDG
(5)
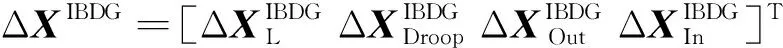
1.2 同步机类电源SBDG
柴油发电机(Diesel Generator)等同步机类分布式电源模型在文献[26,38]中有详细介绍,其励磁环节(AVR/Exciter)和速度控制环节(Speed Governor)如图3所示。
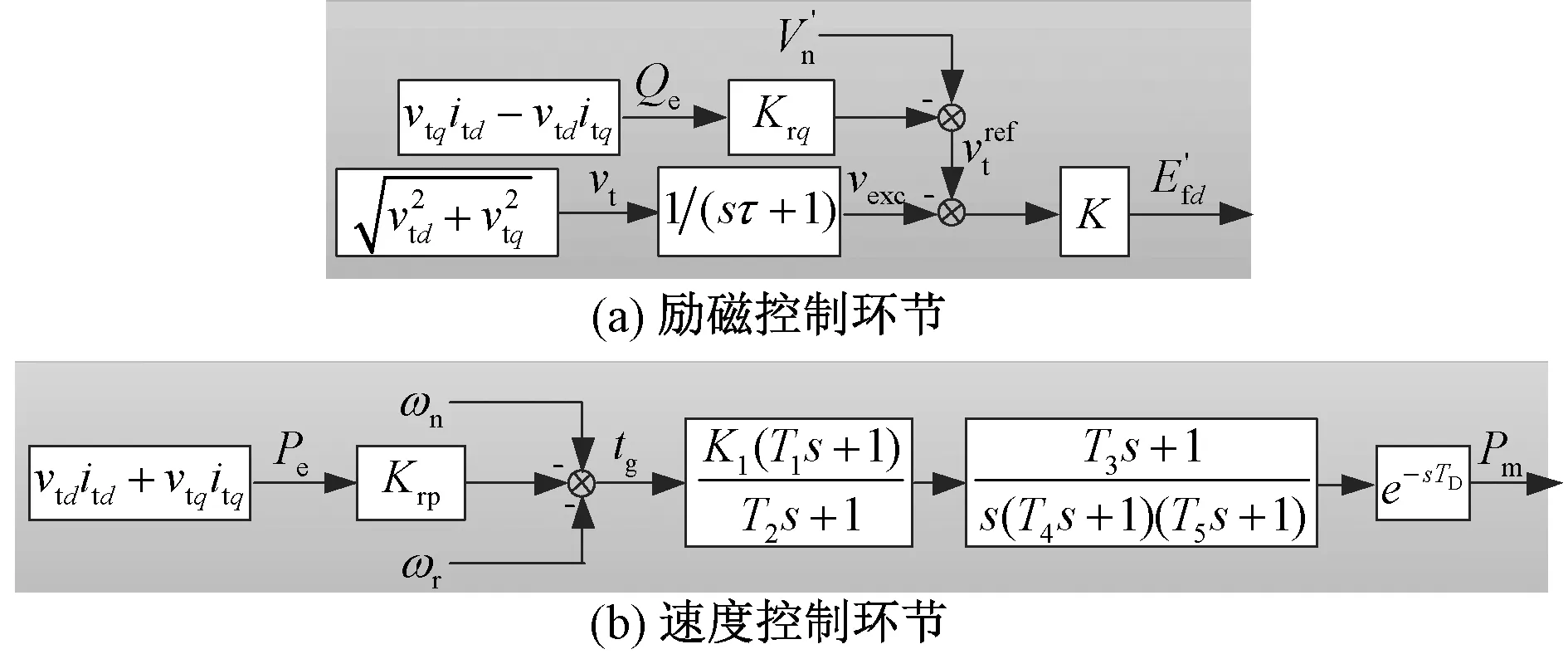
图3 SBDG电源下垂控制Fig. 3 Dynamic droop controller for SBDG
柴油发电机的励磁环节和速度控制环节的动态方程如式(6)~(7)所示。
(6)
(7)

(8)

sΔXSBDG=ASΔXSBDG+BSV[ΔvtdΔvtq]T+BSωΔωcom
[ΔitdΔitq]T=CSΔXSBDG+DS[ΔvtdΔvtq]T
(9)

1.3 坐标转换与电源子系统模型建立
为建立微网统一的小干扰模型,需要将微网中所有电源坐标系转换到统一的参考坐标系,电源自身d-q坐标轴和系统参考D-Q坐标轴间的相对关系如图4所示。

图4 统一参考坐标系转换Fig. 4 Common reference frame transformation
以图2中IBDG为例,将其输出电流[iodioq]从该电源自身d-q坐标系转换到参考D-Q坐标系,有关系式如式(10)。
(10)

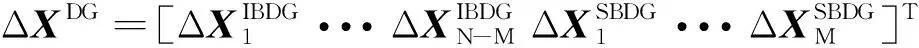
1.4 系统线路/负荷建模与微网模型建立
微网中负荷与线路采用系统参考坐标系,具体建模过程参见文献[12],可写出负荷-线路子系统状态空间模型的一般性表达形式如式(12)。
(12)

sΔXMG=AΔXMG
(13)
联立式(11)~(12)可得到微网系统完整的小信号状态空间模型如式(13)。其中ΔXMG=[ΔXDGΔXN]T表示微网状态变量组成的列向量。为明确电源动态差异对系统稳定性影响,在章节2中采用简化模型分析含两个电源并联的微网系统的稳定性。
2 低频振荡分析与稳定性控制
2.1 双机微网系统低频率振荡降阶分析
SBDG和IBDG并联的系统等效电路[39]如图5(a)所示,其中E1和θ1为IBDG输出电压幅值和相角,Z1=R1+jX1表示IBDG电源输出阻抗和端口线路阻抗之和,U1和δ1为SBDG输出电压幅值和相角,Z2=R2+jX2表示SBDG输出阻抗和端口线路阻抗之和,Z3=R3+jX3为负载阻抗。
图5(a)中星型阻抗网络进行Y-Δ变换等效网络如图5(b)所示,两电源间等效阻抗Z12表达形式如式(14)所示。
Z12∠θZ=R12+jX12=(Z1Z2+Z1Z3+Z2Z3)/Z3
(14)
取电源间相位差为δS=θ1-δ1,可推导IBDG的输出功率S1表达形式如式(15)所示,其中P1/Q1为受到两电源动态影响的功率,P10/Q10为经支路阻抗R13+jX13注入对地节点的功率量、仅受到该电源自身动态特性影响。

图5 IBDG-SBDG电源并联简化模型Fig. 5 Equivalent circuit of IBDG-SBDG in parallel
S1=P1+P10+j(Q1+Q10)
(15)
将式(14)带入式(15)可得
(16)
根据式(16)可得输出功率小干扰形式为
(17)
(18)
同理可得到SBDG输出功率的小干扰形式如式(18)。式(17)~(18)中元素具体表达形式见附录A式(A1)~(A2)。
在线路阻抗呈感性或扰动较小时电源电压幅值变化不大,输出有功主要由相角差ΔδS确定,忽略电压下垂及其他控制动态,式(17)~(18)可简化为
(19)
取SBDG角速度Δωr为系统参考坐标系角速度,根据图2和式(2)可得IBDG的角速度Δω1和电压相角Δθ1的小干扰形式如式(20a)所示,根据图3(b)和式(8)可得SBDG的角速度和电源电压相角Δδ1的小干扰形式如式(20b)所示。
Δω1=-mpΔP1;sΔθ1=Δω1
(20a)
sΔδ1=Δωr
(20b)
式中:GG(s)为SBDG速度控制传递函数,整理式(20)可得相位差ΔδS的小信号表达形式为
将式(19)带入式(21),可得到降阶微网系统的特征方程如式(22)所示
(22)

(23)
SBDG和IBDG角速度动态响应特性不同,当系统受到扰动时电源间功角差ΔδS增大、导致低频振荡。根据式(23)可知,当电源电压相位差δS增大时系统阻尼降低,相位差过大时微网有失稳风险。
2.2 相角锁定控制
前述推导表明DGs间功角相对摇摆导致低频率的相对振荡,SBDG慢动态响应和IBDG的快速响应的差异导致低频率振荡模式阻尼较低。本文提出一种相角锁定控制(Phase-locking Supplementary Control, PSC)如图6,利用IBDGs中逆变器快速响应的特性、抑制电源动态差异导致的低频率振荡。

图6 IBDG的相角锁定控制Fig. 6 Phase-locking Supplementary Control of IBDG
取ωSC为PSC中PI控制环节的输出,作为IBDG下垂控制中角速度ω的补偿项。逆变器下垂控制中PSC环节的输入量包括:(1) IBDG电源输出电压的相角θ以及(2)电源相角在稳态下初始值θ0。则补偿项ωSC为
(24)

(25)
式(21)中的系统特征方程可表示为
(26)
取GG(s)=0并忽略高阶微分项[40],式(26)简化为
(27)
式(27)中特征方程解的阻尼可表示为
′=
(28)
取s=′+jω′并带入式(28),可近似表达出PSC控制的加入对低频振荡模式阻尼增加量为
(29)
对比式(20)~(23)与式(27)~(29),IBDG的功率下垂控制通过采取输出电压相角为反馈,直接作用于由电源间交互作用导致的低频振荡。由于PSC控制采用局部信号作为反馈量、不依赖器件间的快速通信[41],适用于微网系统中电源间交互振荡的抑制。
3 微电网算例分析
图7为含三个分布式电源的微网系统[35],其中IBDGs和SBDG采用章节1.1~1.2中模型,负荷为静态负荷,电源/负荷/线路参数见附录B表B1。电源稳态初始值的求解,需根据DGs的控制方式和微网潮流计算[42]共同确定。本章节从特征值/灵敏度分析,对比不同稳定控制影响等角度,研究电源动态差异导致的稳定性问题。
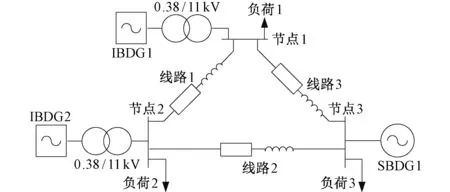
图7 含三个电源的微网算例系统Fig. 7 Microgrid test system with three DGs
3.1 特征值分析
基于式(13)状态空间模型特征矩阵A,可求出微网系统的振荡模式结果如表1所示,其中系统低频段特征值阻尼较低,是微网系统主导振荡模式。

表1 算例微网系统的特征值结果Tab.1 Eigenvalue calculation results of test microgrid
根据参与性因子分析,可识别出上述振荡模式最相关的状态变量和动态环节、并列于表1第五列,发现高频段振荡模式与IBDGs逆变器端口的LCL滤波环节较为相关;中频段振荡模式与IBDGs逆变器内/外环控制较为相关;低频段振荡模式阻尼较差,与IBDGs的功率下垂控制或者SBDG的转子动态较为相关。上述算例系统中模式-11(λ11)是微网系统的主导振荡模式。
模式λ11和λ12的参与性因子分析分析结果和模式的特征向量图(Compass Plot)见图8。
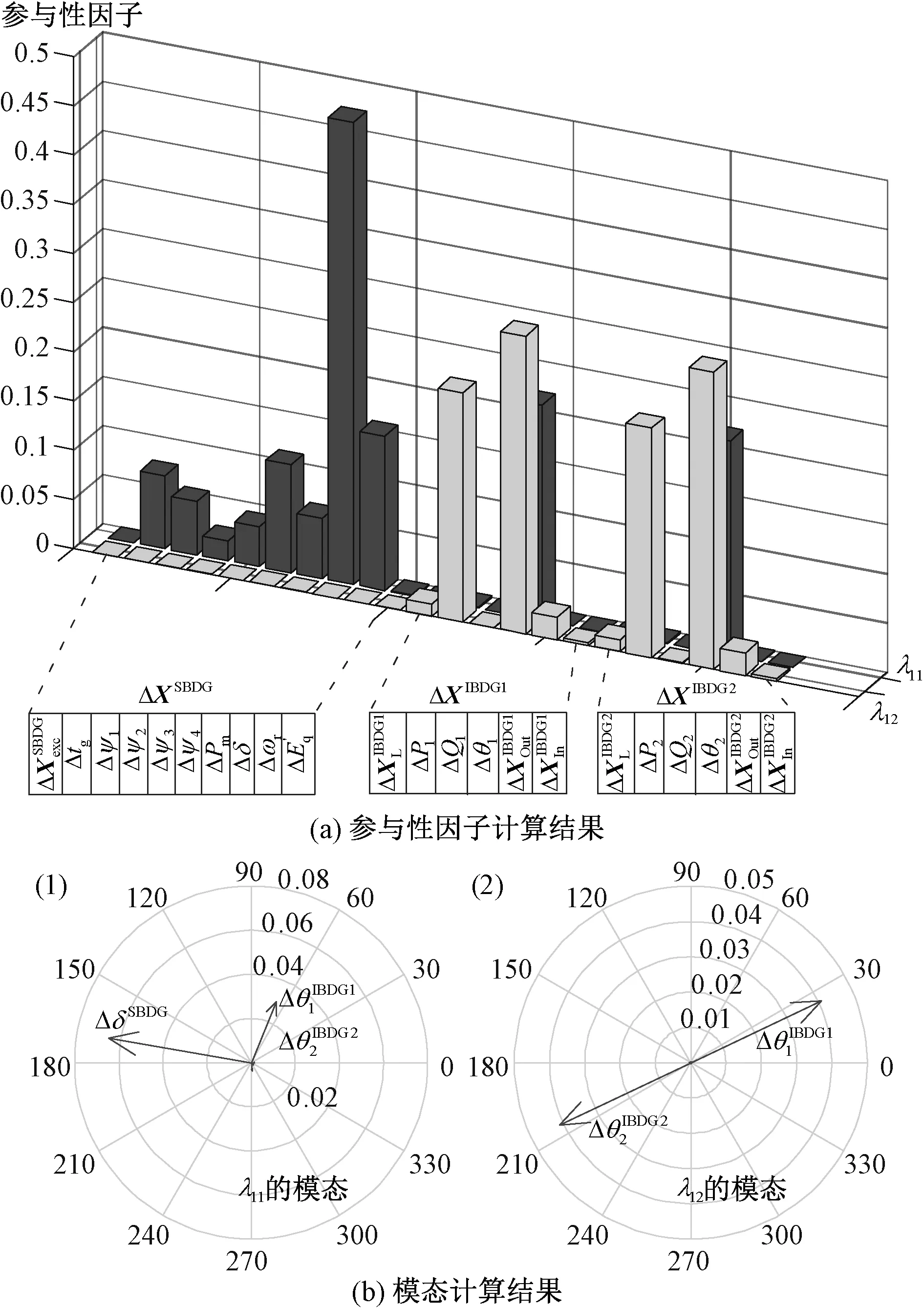
图8 低频振荡模式分析Fig. 8 Analysis of low-frequency oscillation modes

模式λ12中参与因子较高的状态变量分别是IBDG-1下垂控制环节中[Δθ1ΔP1]的以及IBDG-2下垂控制环节中的[Δθ2ΔP2],模态图如图8(b-2),说明该模式主要受到IBDGs下垂控制特性的影响。根据图8中模态计算结果,可知振荡模式λ11和λ12的诱发原因:其中模式λ11表征动态特性不同的电源之间的振荡、是由IBDGs和SBDG间的振荡所产生;模式λ12表示相同动态特性的IBDG-1和IBDG-2之间的振荡、由IBDGs间的交互振荡所产生。
3.2 灵敏度分析
本小节将从系统参数方面,研究其对微网系统稳定性的影响。
3.2.1 下垂控制参数与均流特性
微网中DGs输出有功与功率下垂系数直接相关,在对等均流情况下,每台DG均等承担微网中总负荷[35],针对图7所示三机微网系统有
KrpPe=mp1P1=mp2P2
(30)
在均流情况下同时增大各个分布式电源下垂系数Krp/mp1/mp2,振荡模式λ11和λ12的根轨迹如图9(a)中实线所示,其中初始状态和参数变化时模式位置用三角形和空心圆圈表示。在下垂系数从0.002 p.u.增大到0.006 p.u.的过程中,受IBDG换流器下垂控制特性影响的振荡模式λ12阻尼迅速降低、向着复平面的右半平面移动,当下垂参数增大至0.005 8 p.u.时系统失稳;此时模式λ11向复平面左上方移动,SBDG和IBDGs间振荡阻尼增大。

图9 低频特征值受下垂控制参数影响根轨迹图Fig. 9 Trace of low-frequency modes affected by droop gains
在非均流情况下,电源下垂控制参数的增大对应其输出功率的降低。当SBDG下垂系数Krp保持不变、IBDGs下垂控制参数mp1和mp2从0.002 p.u.增大到0.007 p.u.时,IBDGs输出功率降低、SBDG输出功率增大,振荡模式λ11和λ12的根轨迹如图9(b)中虚线所示,随IBDGs渗透率降低、振荡模式λ12阻尼变差,IBDGs下垂参数增大至0.006 6 p.u.时系统失稳,而SBDGs渗透率增大提高了振荡模式λ11的阻尼。
当IBDGs下垂控制参数不变、SBDG下垂参数Krp增大时,SBDG的输出功率降低,对应振荡模式的根轨迹如图9(b)中实线所示,特征值在复平面上的位置用星号所示,此时交互振荡模式λ11的阻尼随着SBDG渗透率的降低而减小,在下垂参数为0.004 7 p.u.时系统失稳,但此时振荡模式λ12的变化并不明显。综上所述,在保证IBDGs下垂特性相关的振荡模式λ11阻尼大于交互振荡模式λ12阻尼的前提下,适当的通过增大IBDG的下垂控制参数或降低SBDG的下垂参数、可以提高SBDG渗透率、增强微网系统的整体稳定性。
3.2.2 其他参数
为不失一般性,讨论其他参数对低频率振荡模式的影响。针对IBDGs逆变器控制外环,当增大IBDGs的外环比例系数kup从3到8时,振荡模式的位置在图10(a)中以空心圆圈表示,说明增大IBDG逆变器外环比例系数主要影响振荡模式λ12的虚部;当仅增大逆变器外环积分系数kui从90到210时,振荡模式的位置在图10(a)中以星号表示,说明kui增大可以提高模式λ12的阻尼。
针对IBDGs内环的比例和积分系数,在图10(b)中以空心圆圈和星号分别表示kip从3.5增大到6.5以及kii从560增大到1 000的模式位置,实线所示根轨迹说明增大内环比例系数主要增大模式λ12的频率,虚线所示根轨迹说明内环积分系数的增大会降低λ12的阻尼。综合图10(a)-(b),发现IBDGs换流器控制参数对振荡模式λ11的影响较小,而模式λ12随参数变化规律同仅含IBDGs的微网系统相似[43,44],说明不同类型电源的接入并未改变同类型电源间交互振荡的特性。
针对SBDG的励磁控制和速度控制环节,微网系统低频率模式随励磁增益K和速度控制增益K1的根轨迹如图10(c)和(d)所示。不同于传统系统中降低励磁增益会增大同步机振荡模式的阻尼[26],当将K从92降低至68时,模式λ12的阻尼降低。降低速度控制增益K1直接影响到机电振荡回路中的负反馈量,提高振荡模式λ12的阻尼。
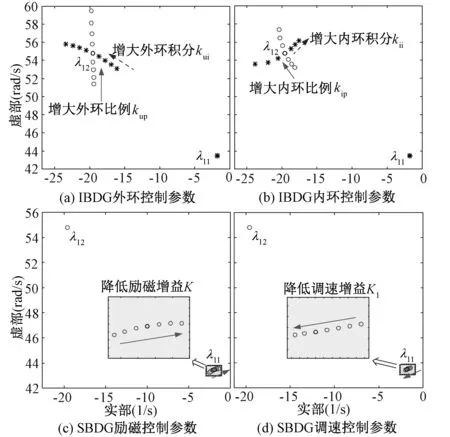
图10 主导模式受其他控制参数影响根轨迹Fig. 10 Critical modes affected by other control parameters
3.3 PSC控制与时域仿真验证
为验证上述分析及所提方法的有效性,使用Matlab/Simulink软件构建图7所示算例系统,首先分析如下两种情况:(1)在均流条件下系统稳定的情况,取Krp=mp1mp2=0.002 p.u.为系统初始状态,称为运行点①;(2)在均流条件下系统失稳的情况,取有功下垂系数为0.005 8 p.u.,称为运行点②。在0.3秒时于节点3发生幅值为0.18 p.u.的有功负荷降低,运行点①和②处仿真曲线见图11。

图11 算例微网系统均流情况仿真图Fig. 11 Simulation of equal power-sharing microgrid
额外阻尼控制PSC作用于电源间交互振荡的机理见章节2.2。以运行点①为例,低频振荡模式受PSC控制参数影响的计算结果见下表2。
从表2中可以看出,额外阻尼控制PSC的加入有助于增大SBDG-IBDGs间振荡的阻尼,也对IBDGs间振荡模式产生一定的影响。PSC对不同类型电源间振荡模式(λ11)主要影响其实部,增大比例系数可以提高模式阻尼;对IBDGs间振荡模式λ12则同时影响其实部和虚部,比例系数的增大可提高λ12的阻尼、积分系数的增大可提高λ12的振荡频率。

表2 系统低频振荡模式受PSC控制的影响Tab.2 Influence of PSC on low-frequency modes
针对非均流失稳的情况,取Krp为0.005 p.u.,mp1=mp2为0.002 p.u.,称为运行点③,系统在0.3秒时于节点3发生了幅值为0.18 p.u.的有功负荷降低,在2秒时IBDGs的换流器中加入PSC控制,电源的输出功率和角速度如图12所示。在前2秒内,下垂系数Krp增大引起SBDG-IBDGs间交互作用的增强、导致了发散振荡,对应图9(b)中振荡模式λ11的失稳。
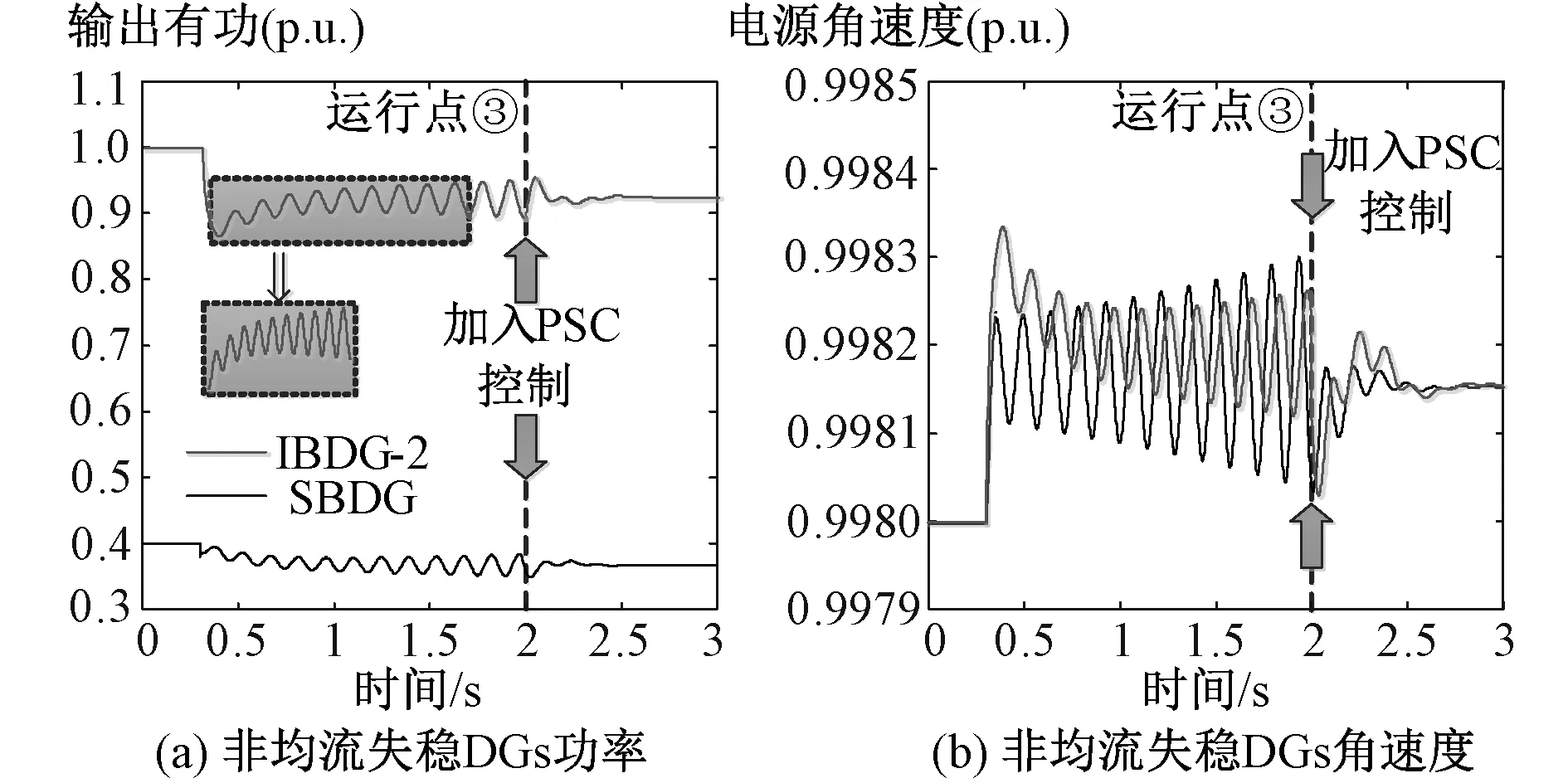
图12 算例微网系统非均流情况仿真图Fig. 12 Simulation of unequal power-sharing microgrid
在仿真的第2秒,启用额外阻尼控制PSC以抑制DGs间的交互作用,可发现PSC的加入抑制了原本存在的发散性振荡,利用IBDGs逆变器控制的快速响应特性抑制了SBDG-IBDGs间存在的动态交互,验证了所提方法的有效性。
4 多微电网算例系统分析
4.1 多微网算例系统-1
本小节采用图13所示多微网系统[26],探究电源间的交互振荡以及PSC稳定性增强效果。

图13 含三个子微网的多微网算例系统-1Fig. 13 Test system MMG-1 with three sub-MGs
微网通过开关SWi,i=0,1,2,3互联,当SW0打开而其他开关闭合时,多微网系统处于孤网运行状态、三个子网并行连接。DGs采用章节1.1~1.2中模型,系统参数见附录B表B2。


表3 多微网系统低频振荡模式计算结果Tab.3 Low-frequency modes results of tested MMG

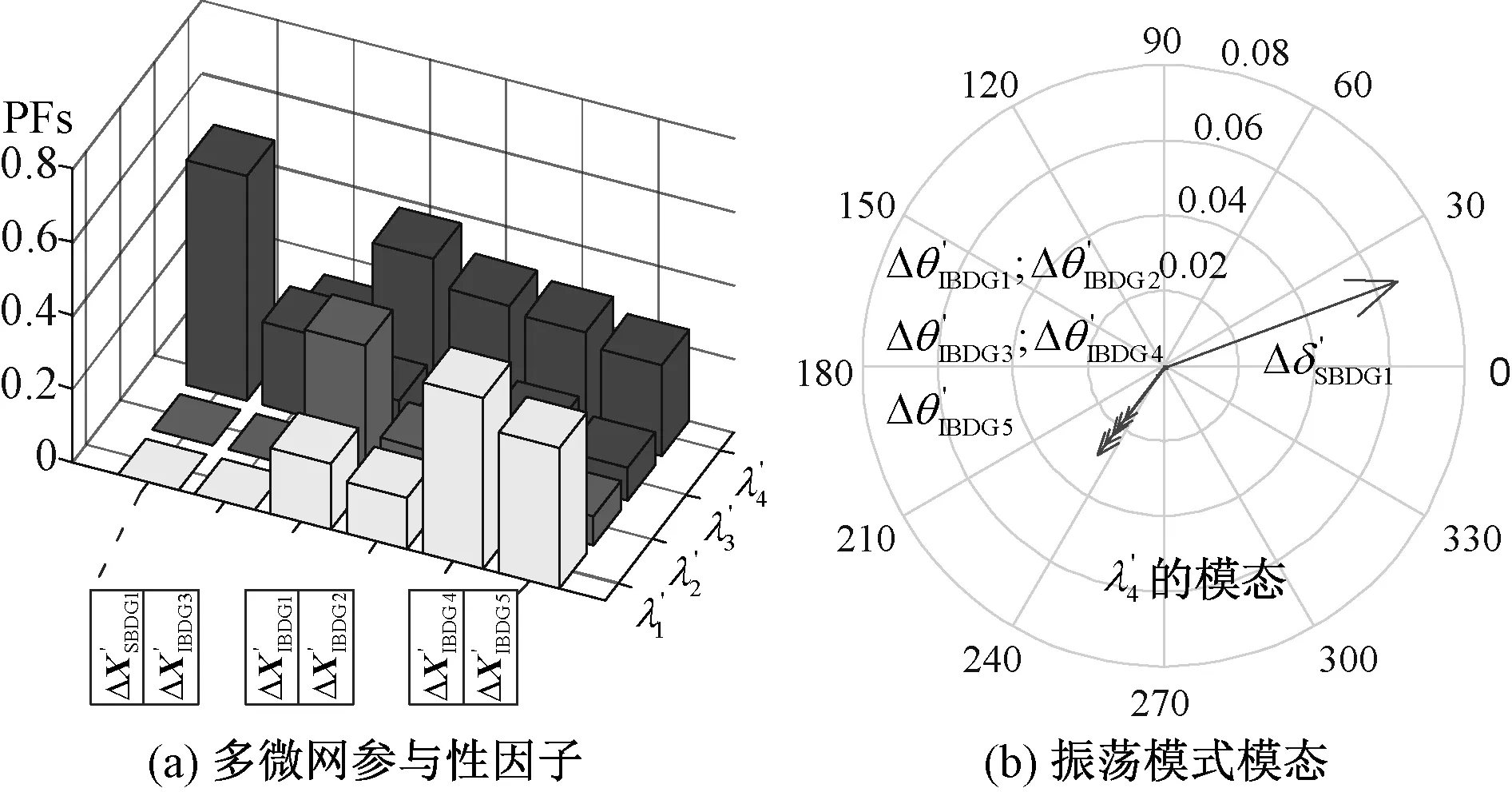
图14 多微网低频振荡模式分析Fig. 14 Analysis of MMG low-frequency modes

多微网算例系统-1中负荷6于仿真第0.3 s发生0.24 p.u.的有功负荷降低,时域仿真结果见图15。

图15 多微网系统算例-1仿真图Fig. 15 Simulation results of MMG-1
子微网3内电源输出有功功率的仿真曲线如图15(a)所示,可见IBDG4和IBDG5之间的交互振荡引起了联络线上交换功率的发散性振荡如图15(c)所示、以及其他子微网中电源的交互振荡如图15(d)所示,各电源角速度的仿真曲线如图15(b)所示。在仿真第2秒加入PSC控制,多微网系统中电源间的交互振荡得到了有效的抑制,同时联络线上的传输功率振荡得到平抑。
4.2 多微网算例系统-2
多台IBDGs和SBDGs并联运行的情况也是较常出现的,本小节研究图16所示多微网系统[35]。

图16 含两个子微网的多微网算例系统-2Fig. 16 Test system MMG-2 with two sub-MGs


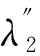
取DGs下垂系数为0.004 p.u.时微网均流稳态情况为运行点④;取DGs下垂系数为0.006 p.u.时的均流失稳情况为运行点⑤。两运行点处的仿真结果如图17中分别用实线和虚线表示。

图17 多微网系统算例-2仿真图:均流情况Fig. 17 Simulation results of equal power sharing MMG-2
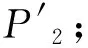

上述非均流失稳情况的时域仿真结果见图18,在仿真的第0.3秒增大负荷4的有功10%,在仿真的第2秒加入PSC控制:仿真前2秒的发散振荡曲线说明系统在该参数条件下是小干扰不稳定的,验证前述稳定分析的正确性;在加入PSC控制后,电源输出功率和微网间交换功率逐渐收敛、多微网系统趋于稳定,证明PSC控制的有效性。
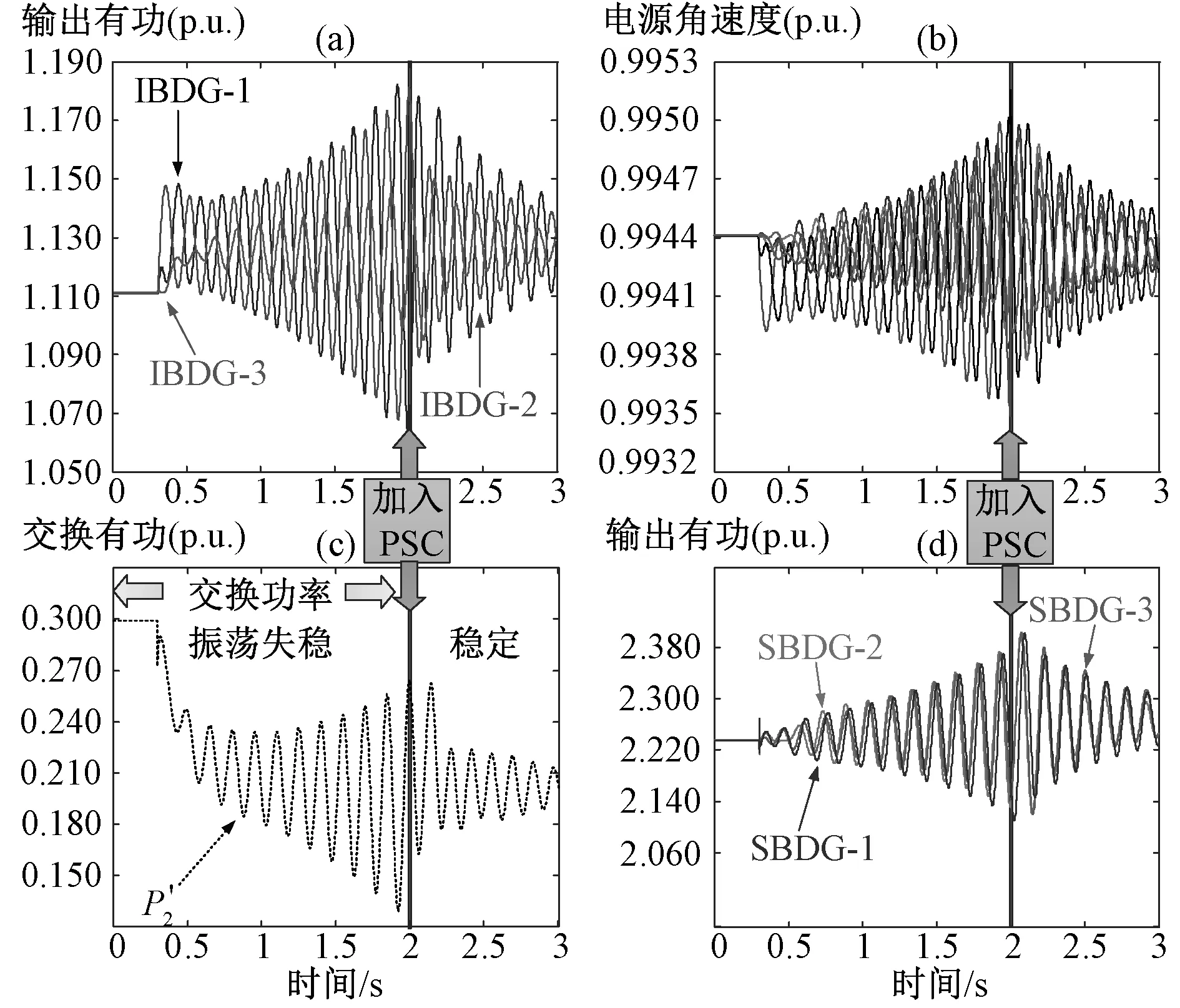
图18 多微网系统算例-2仿真图:非均流情况Fig. 18 Simulation results of unequal power sharing MMG-2
章节3和章节4中的算例分析了微网系统和多微网系统中由于DGs间交互作用导致的低频振荡,探究了SBDG与IBDGs以及IBDGs之间交互振荡导致的微网系统低频失稳,并通过PSC额外阻尼控制改善了微网系统稳定特性,验证了文章分析及所提控制方案的有效性。
5 结 论
本文通过建立含不同种类分布式电源的微网系统小信号状态空间模型,研究了分布式电源动态特性差异导致的低频率范围内稳定特性,主要工作和结论如下:
(1)通过特征值、参与因子分析,识别微网系统内存在的电源间交互振荡模式,分析微网下垂控制特性以及其他参数对系统低频率主导振荡模式的影响,发现微网系统均流特性、有功下垂控制、对电源间交互振荡阻尼有显著影响;
(2)通过对系统和控制环节的简化,推导得到电源交互作用导致低频振荡模式阻尼的表达形式,分析同步机类、逆变器类分布式电源间动态特性差异导致的微网低频率振荡的机理;
(3)为应对分布式电源间交互导致的低频振荡失稳,文章提出了一种相角锁定控制,以增加电源间交互振荡模式的阻尼。采用微网和多微网算例验证文章分析的正确性和所提控制的有效性。
