基于二次分解的风机齿轮箱油温预测模型
2022-02-18杨少梅王廉茹
杨少梅, 王廉茹
(华北电力大学 经济与管理学院,河北 保定 071003)
0 引 言
近年来,中国风电装机容量不断上升。2020年中国风电新增装机容量7 167 MW,风电累计装机容量达到281.72 GW[1]。风电装机量的增加,使得如何减少运行而维护成本已成为风电场面临的日益严峻的挑战[2]。我国风电装备通常在运转5年之内出现关键故障[3]。工作寿命在20年的风电机组运维成本大约占风场收入的10%~15%,海上风电机组则高达20%~25%[4]。在我国,多数采用计划检修和事后检修的方式来处理风电机组的故障。其中计划维修是指机组运行2 500 h或5 000 h后进行例行维护,无法准确掌握机组的运行状态并发现问题;事后维修的缺点是设备维修耗时太长且维修费用昂贵[5]。
为了保证电力系统运行的安全,风力发电机组的早期故障检测显得尤为重要[6]。研究表明,风力发电机组变速箱是一个容易发生故障的关键部件[7]。目前,风力发电机组齿轮箱故障预测的研究主要集中在振动信号分析和声发射信号[8],但对齿轮箱温度的研究较少。润滑系统作为齿轮箱的核心系统之一,具有传递载荷、适应接触速度、散热、减少摩擦等功能[9]。如果润滑系统的油温过高,齿面润滑不良,然后过热,导致齿轮磨损、擦伤、微点蚀、点蚀等典型故障[10]。如果能准确预测油温的趋势,可以提前采取维修措施,实现齿轮箱的早期维修。
目前,深度学习方法是时间序列预测领域最流行的预测方法,并得到了学术界的广泛认可[11]。刘跃飞等利用支持向量机(Support Vector Machine, SVM)对齿轮箱油温进行预测并基于此设定预警阈值[3],Qing等利用长-短期记忆(Long Short-Term Memory, LSTM)方法建立了太阳辐照度的预测模型[12]。结果表明,LSTM的预测效果优于传统的浅层神经网络。Li等[13]将递归神经网络(Recurrent neural network, RNN)作为主要预测因子,对滚动轴承的状态趋势进行预测。
1 风机齿轮箱油温预测算法
1.1 聚类经验模态分解(EEMD)
聚类经验模态分解(Ensemble empirical mode decomposition, EEMD)是经验模态分解(Empirical mode decomposition, EMD)的改进方法,其计算步骤如下:
(1)假设x(t)是原始信号,将随机白噪声信号nj(t)加到x(t)上:
xj(t)=x(t)+nj(t)
(1)
式中:xj(t)为添加噪声后的信号;j为整数且j∈[1,M];M表示试验次数。
(2)利用EMD分解为一系列固有模态函数(IMF):
(2)
式中:ci,j为第j次试验的第i个IMF;rNj为第j次试验的剩余部分;Nj为第j次试验得到的IMFs数量。
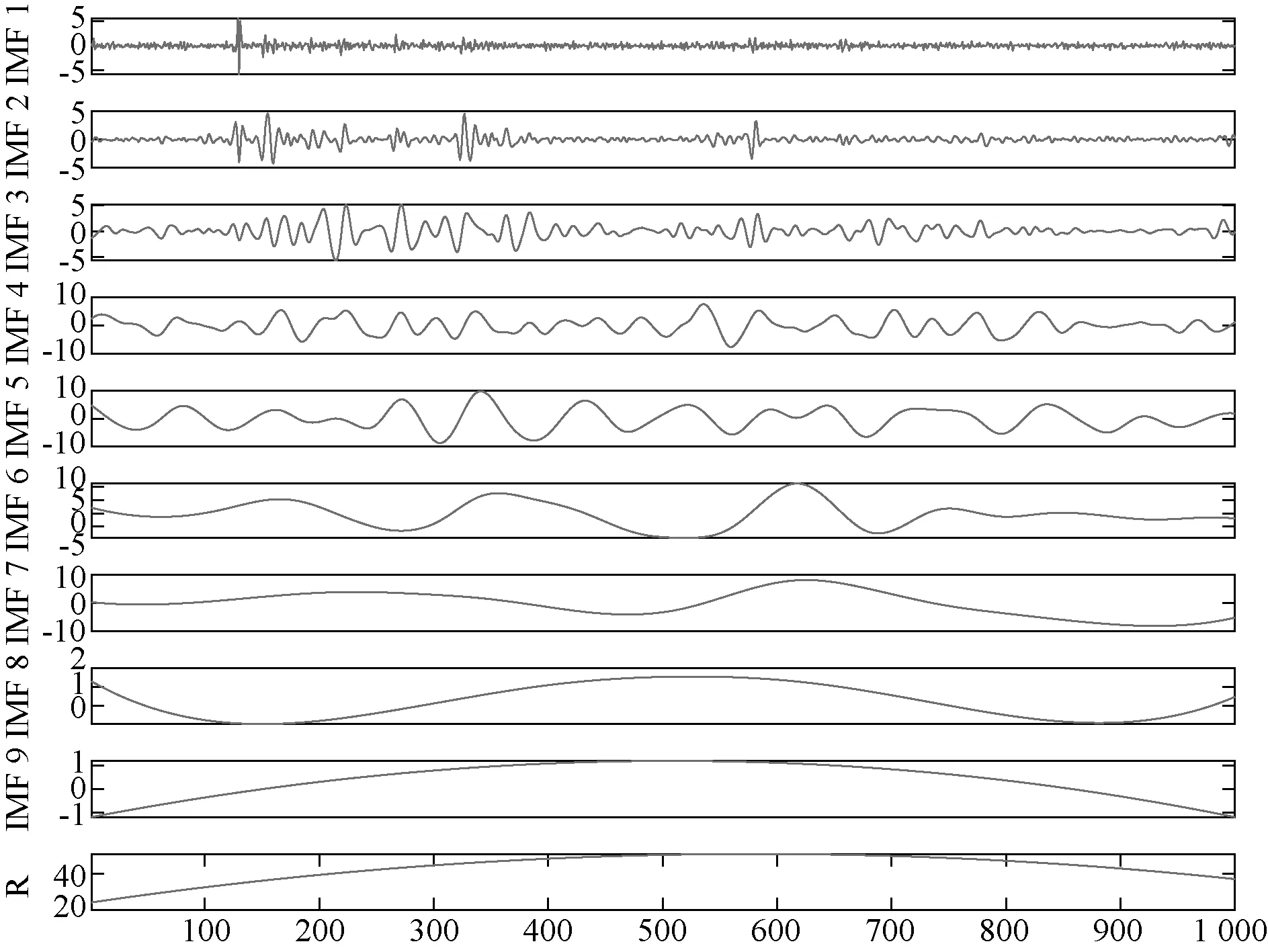
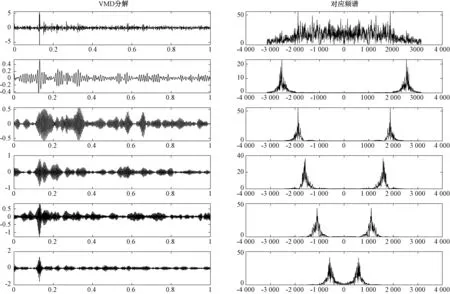
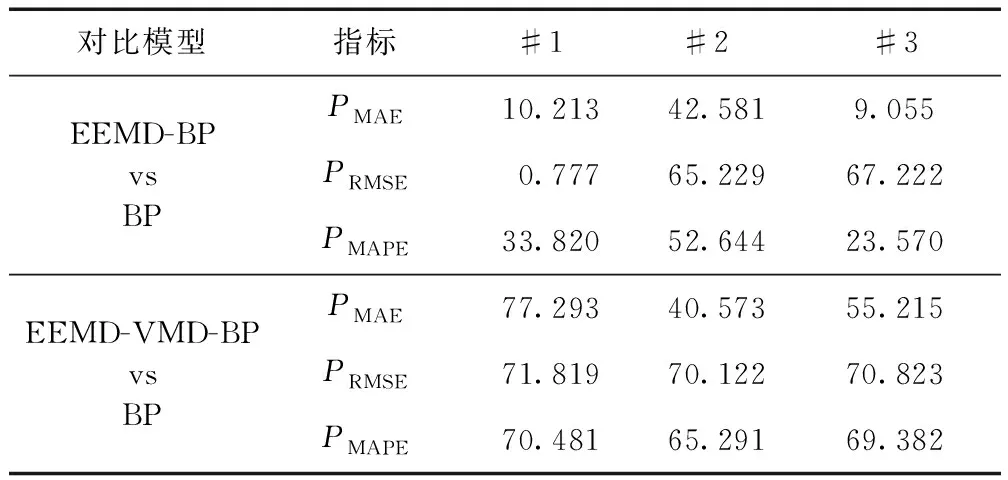
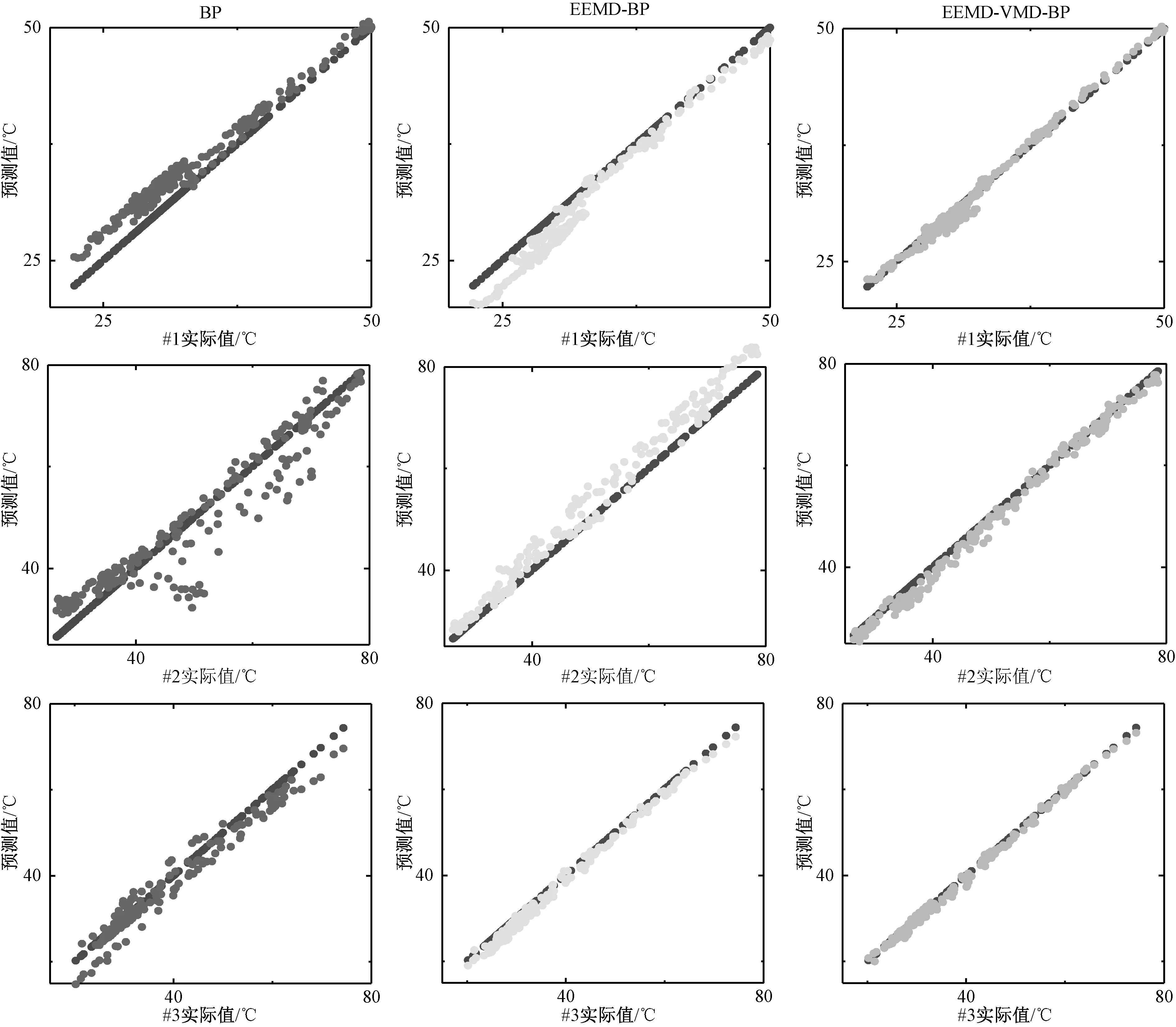
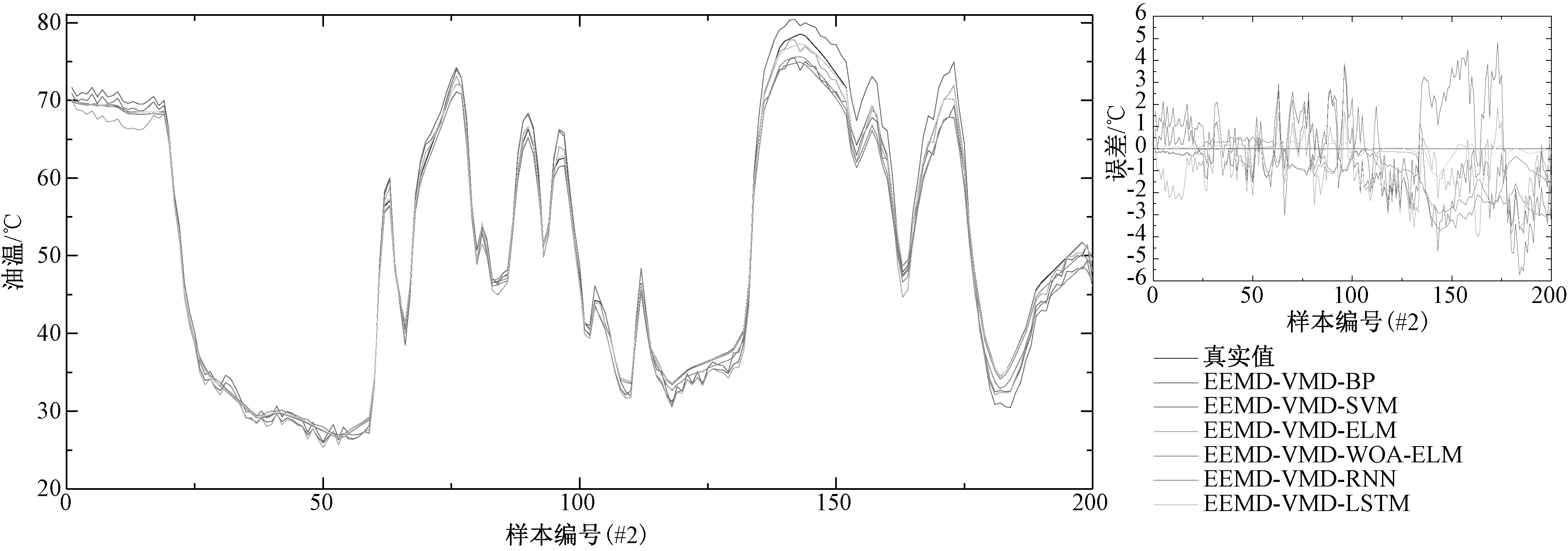
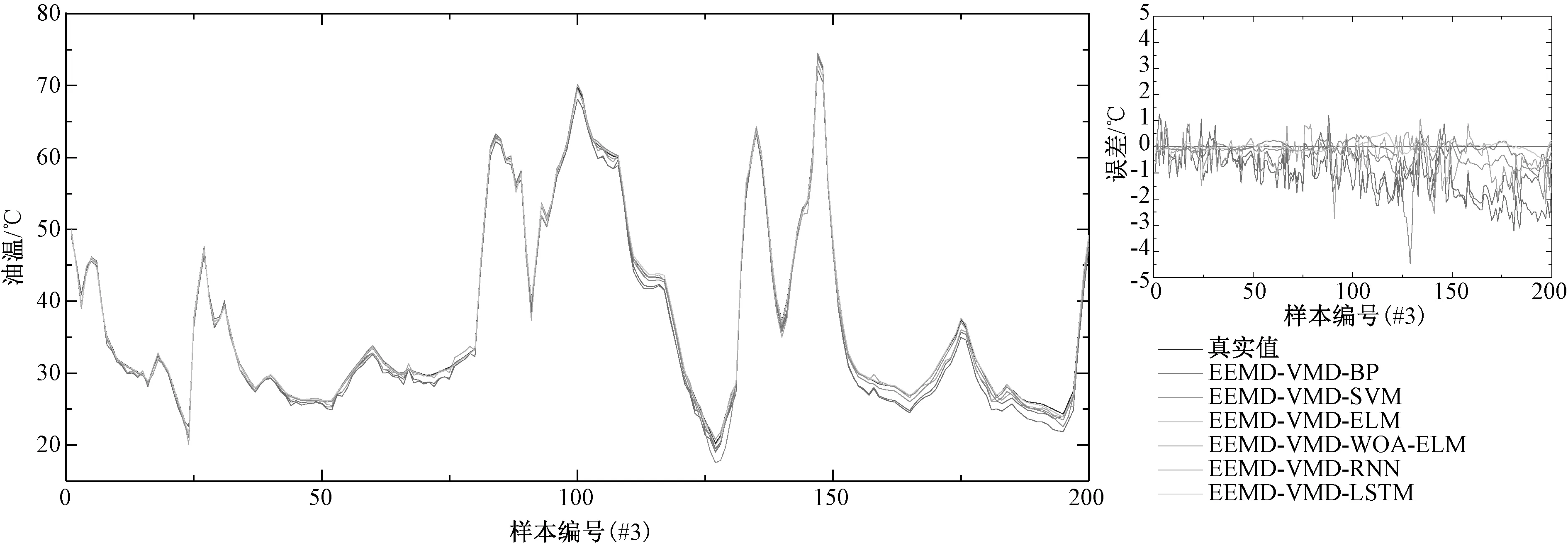
(3)如果j (4)得到I=min(N1,N2, …,NM),同时计算分解的相应IMF的集合平均值作为最终结果: (3) 式中:i=1, 2, …,I。 (5)ci(i=1, 2, …,I)表示IMF的平均值。 Alcaraz和Rieta 在2010年提出了一种新的时间序列信息量量化方法[14],即样本熵(Sample entropy, SE)。计算步骤如下: (1)将序列x(1),x(2), …,x(N)构建成m维向量: Xm(i)=[x(i),x(i+1),…,x(i+m-1)] (4) 式中:i是整数,且i∈[1,N-m+1]。 (2)d[Xm(i),Xm(j)]是向量Xm(i)和向量Xm(j)间的距离,计算方法如式(5): d[Xm(i),Xm(j)]=max|x(i+k)-x(j+k)| (5) 式中:k为整数,且k∈[1,m-1], 1≤i,j≤N-m+1,i≠j。 (3)设置相似性容忍值r。d[Xm(i),Xm(j)] (6) 计算平均值,方法如式(7): (7) 计算m+1处的向量,根据式(8): (8) 同样,计算平均值: (9) (4)序列的样本熵表示为 (10) 实际上,N取一个有限值,其结果估计如式(11): SampEn(m,r,N)=-ln[Am(r)/Bm(r)] (11) 变分模态分解(Variational mode decomposition, VMD)由Dragomiretskiy和Zosso于2014年提出[15]。它是一种新的信号分解估计方法。其核心思想是在原始信号的基础上构造一组N个不同的带限本征模函数(BLIMF),使每个BLIMF的估计带宽之和最小。BLIMF的公式如式(12): vi(t)=Ui(t)cos(wi(t)) (12) 式中:Ui(t)和ωi(t)分别表示BLIMF分量的瞬时振幅和瞬时相位。 VMD算法的步骤如下: (3)更新每个BLIMF分量和中心频率: (13) (14) 式中:β为次要的惩罚因素。 (4)拉格朗日算子通过以下公式迭代更新: (15) 式中:τ表示噪声容忍参数。 (5)确定是否符合下列终止条件: (16) 式中:ξ为判别值。如果符合,则停止迭代。通过对每个分量进行傅立叶逆变换,得到最终分解的时域BLIMF分量集。 LSTM神经网络最早由Schmidhuber和Hochreiter提出[16],由于能更好地发现长期依赖关系而被广泛用于处理序列信息,如语音识别、机器翻译等。LSTM每个神经元的结构包括一个记忆储存 (Cell) 和三个门控 (Gates) 设置,Cell记录神经元状态, 输入门 (Input Gate) 和输出门 (Output Gate) 用来接收、输出参数和修正参数, 遗忘门 (Forget Gate) 用来控制上一单元状态的被遗忘程度[17]。 综上所述,本文的研究主要由三部分组成,如图1所示。 图1 油温预测流程图Fig. 1 Flow chart of oil temperature prediction system 第一部分,分解。将原始数据输入模型,通过EEMD得到多个复杂度和非线性度较低的IMF分量。第二部分,重构。本节分为两个步骤,首先用VMD对上一步得到的IMF1分量进行进一步分解,得到新的分量。同时,利用SE对剩余子序列的相似度进行量化,并对相似度较高的子序列进行整合。第三部分,预测。将IMF1再次分解后的序列和重建得到的新的子序列输入到LSTM神经网络中,得到每个子序列的预测结果。将各子序列的预测结果相加,得到最终的预测结果。 本文选取来自某风电场的三组1 000个采样点的SCADA(监控与数据采集)系统采集的油温数据,油温数据为每分钟读取一次,三组数据分别间隔10 min、30 min钟、50 min取值,对模型的有效性进行验证。SCADA系统采集的油温数据#1和#2来自不同的齿轮箱,数据#1和#3来自同一齿轮箱。表1显示了这些油温时间序列的统计分析。原油温度数据的波动特征如图2~图4所示。 在本研究中,将选取前800个样本点作为训练数据,将后200个样本点将作为测试集来验证该模型的性能。 表1 数据基本信息Tab.1 Statistical description of datasets 图2 数据集#1原始数据Fig. 2 Raw oil temperature data #1 图3 数据集#2原始数据Fig. 3 Raw oil temperature data #2 图4 数据集#3原始数据Fig. 4 Raw oil temperature data #3 本研究采用了3个经典指标,即平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)。此外,还采用了MAE(PMAE)、RMSE(PRMSE)和MAPE(PMAPE)的改善率,可以直接比较不同模型的优缺点。 (17) 式中:D(i)表示数据的真实值;D′(i)表示数据的预测值;n表示样本数量。 (18) 式中:下标1表示基准模型,下标2表示比较模型。 本研究提出的预测模型的第一步是应用EEMD对原始数据进行分解。图5显示了#1分解前后的结果。经过EEMD处理后,原始序列被分解成10个子序列。与原始序列相比,子序列具有更明显的波动规律,有助于预测模型更好地把握数据波动特征。 图5 数据集#1分解图Fig. 5 Decomposition result of dataset #1 在得到3个数据集的分解结果后,计算了所有子序列的样本熵。如图6所示,所有子序列的样本熵显示出类似的趋势。可以看出IMF1的样本熵比其他子序列的样本熵要高得多。这表明IMF1远比其他子序列复杂。因此,对IMF1进行再分解是提高预测精度的合理尝试。 图6 序列样本熵值Fig. 6 Sample entropy of each sequence 利用VMD对IMF1进行分解。图7是对数据集#1的IMF1的再分解结果以及对应于每个序列的光谱。从图7可以看出,具有高复杂性的IMF1被分解为5个子序列。与IMF1相比,子序列波动更为规律。此操作可进一步提高预测的准确性。 图7 数据集#1中IMF1分解结果Fig. 7 Decomposition result of IMF1 of dataset #1 本节中的另一个步骤是集成IMFs和R(IMF1除外)。根据样本熵的结果,将相似的子序列整合成一个新的序列Fm。重构的结果总结在表2中。 表2 序列重构Tab.2 Result of sequence reconstruction 3.3.1 实验Ⅰ:比较不同预测方法 为了证明LSTM在油温预测中具有有效的预测性能,本文将LSTM与BP、SVM、ELM和WOA-ELM等几种经典神经网络进行了比较。此外,还将LSTM方法与门控神经网络RNN进行了比较,证明了LSTM方法的优越性。对数据集#1、#2、#3用不同方法进行预测,结果如表3所示。 表3 不同模型的预测误差Tab.3 Prediction error of different models 3.3.2 实验Ⅱ:验证分解方法的有效性 为了验证所提出的二次分解模型可以提高神经网络模型预测的准确度,选用BP模型作为基准模型,分别用BP模型预测的结果与EEMD-BP和EEMD-VMD-BP的预测结果进行对比,图8是一个散点图,给出了加入分解后的模型与基准模型之间的对比,表4给出了这些模型的误差对比结果,表5给出了不同模型之间预测误差的提升率。 3.3.3 实验Ⅲ:比较不同模型对二次分解后的新序列进行预测的误差 为了验证所提出模型的先进性和创新性,有必要将所提出的模型与现有模型进行比较。包括进行二次分解后的BP、SVM、EIM、WOA-ELM和RNN。这些采用时间序列预测方法的先进模型在风速、大气污染物浓度和负荷预测中是有效的。与这些模型的比较验证了所提出的EEMD-VMD-LSTM模型的应用价值。图9~图11显示了6个相关模型的预测结果和误差结果。图12给出了6个相关模型的MAE、MAPE和RMSE结果,可以看出本文所提出的模型的优越性。 表4 不同模型的预测误差Tab.4 Prediction error of different models 表5 不同模型的预测误差改善率Tab.5 Prediction error improvement rate of different models(%) 图8 不同模型预测效果对比Fig. 8 Comparison of prediction results of different models 图9 数据集#1的预测结果和误差Fig. 9 Prediction results and errors of dataset #1 图10 数据集#2的预测结果和误差Fig. 10 Prediction results and errors of dataset #2 图11 数据集#3的预测结果和误差Fig. 11 Prediction results and errors of dataset #3 图12 不同模型的误差结果Fig. 12 Error results of different models 油温预测对于齿轮箱的实时检测以及后续的故障诊断非常有用。本文提出了一种基于二次分解方法和LSTM网络相结合的油温预测模型。首先,利用EEMD对原始序列进行预处理。然后,对每个子序列进行重构,用VMD分解样本熵最高的IMF1。同时,计算了剩余子序列的样本熵,并将熵值相近的序列进行了综合。然后,利用LSTM对各子序列进行预测。根据实验结果和讨论,得出如下结论: 本文提出的预测模型具有良好的预测性能。在三个比较实验中,本文提出的模型的预测结果好于其他模型。实验结果证明,该模型能准确地捕捉齿轮箱油温的波动规律,具有较强的自适应能力。此外,引入样本熵弥补了分解算法造成的操作冗余,提高了预测效率。该模型可为齿轮箱油温提供更可靠、更有效的预测信息,实现了风电机组齿轮箱状态的实时检测,能提前预防齿轮磨损、擦伤、微点蚀、点蚀等典型故障的发生。 该模型能准确预测齿轮箱的油温序列,为齿轮箱的实时检测提供了有意义的参考。今后将考虑将其运用到风机齿轮箱油温预测及故障诊断中。1.2 样本熵(SE)
1.3 变分模态分解(VMD)

1.4 长短期记忆人工神经网络(LSTM)
1.5 预测模型结构

2 数据来源及评价指标
2.1 数据来源

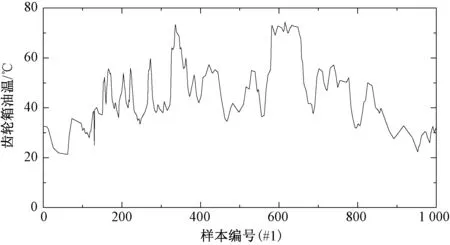
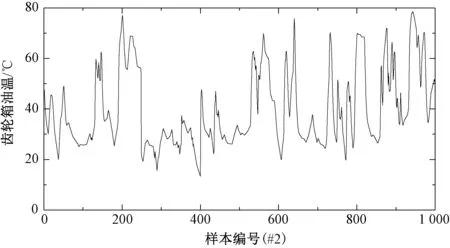

2.2 评价指标
3 模型有效性验证
3.1 序列分解
3.2 输入重构


3.3 油温预测




4 结 论
