基于PSO-Lasso算法的电站湿法脱硫出口SO2浓度预测

2022-02-18郑茗友赵文杰王建峰郄英杰

华北电力大学学报(自然科学版) 2022年1期

郑茗友，王伟，赵文杰，王建峰，郄英杰

(1.华北电力大学控制与计算机工程学院，河北保定 071003；2.山西漳山发电有限责任公司，山西长治 046021)

0 引言

我国是世界上最大的煤炭生产国和消费国，煤炭燃烧所产生的SO2、 NOX、粉尘等大气污染物是现阶段我国环境治理的关键[1]。燃煤电厂现已成为污染物排放的主要来源，其中的SO2主要通过脱硫系统来进行脱除，在我国燃煤电厂中石灰石—石膏湿法脱硫技术应用最为广泛。随着环保要求的日益严格，现阶段电厂 SO2出口浓度一般都控制在35 mg/m3以下[2]，SO2的优化控制已经成为各发电企业重点的研究方向。优化控制策略的设计离不开脱硫效率计算的支撑。虽然电厂存在着大量的数据监测设备，烟气分析仪表也可以实时监测SO2的浓度。但监测出的数据往往存在着滞后性，不能够及时反映工况的变化，同时监测设备也存在着老化、故障等问题，使测量结果存在较大误差。如果能够使用数学方法，通过一定的运算规则直接计算得到脱硫系统的出口SO2浓度，将有效提高脱硫系统的控制水平。随着人工智能的兴起，大量的智能算法在脱硫出口浓度预测中得以应用，张浩[3]提出了基于聚类的偏最小二乘支持向量机脱硫出口浓度预测模型。将聚类分析、偏最小二乘法(PLS)、最小二乘支持向量机(LSSVM)结合起来，达到了良好的预测效果。崔仕文[4]等提出了基于偏最小二乘支持向量机的脱硫出口浓度预测模型，使用PLS方法进行了对脱硫效率影响因素的分析。并使用支持向量机(SVM)进行建模，取得了良好的效果，但模型计算复杂度较高。神经网络因其具有优异的自学习功能在预测方面应用广泛。马双忱等[5]提出基于深度神经网络的脱硫系统预测模型。苏翔鹏等[6]基于RBF神经网络对双碱法脱硫塔SO2排放量进行了预测；李斌等[7]提出了基于T-S模糊神经网络的脱硫出口浓度预测模型，李军红等[8]提出了广义回归神经网络对脱硫效率的预测。神经网络具有容错度高，普适性强的优点，但因其训练存在随机性，容易发生过拟合现象。

以上的方法因为其复杂的结构需要在一定的独立软件中进行仿真研究，难以得到具体的预测模型。同时大多数的研究者将目光放在脱硫效率的影响因素与脱硫效率之间的关系，但在实际的应用中，发电企业主要关注的是脱硫系统出口SO2浓度是否达标，鉴于此本文提出使用Lasso算法进行脱硫系统出口浓度的预测。将各参数以最优的函数形式组合起来，并结合正交化法则进行训练数据的选取，有效降低了模型的计算复杂度，提高了训练样本的丰富性，使模型具有较高的预测精度。使用某电厂实际的脱硫系统运行数据进行训练和测试，并验证模型的预测精度与稳定性。

1 石灰石-石膏湿法脱硫系统

1.1 反应机理

湿法脱硫系统主要工艺原理是通过浆液循环泵将浆液池中的石灰石浆液喷洒到脱硫塔的顶部，含硫烟气经过引风机引入吸收塔自下而上的与石灰石浆液进行接触，使烟气中的SO2与石灰石浆液充分反应，化学反应式如下：

CaCo3+2SO2+H2O→Ca(HSO3)2+CO2

(1)

反应后的产物经氧化风机氧化后生成石膏，化学反应式如下：

Ca(HSO3)2+O2+CaCO3+3H2O→

2CaSO3·2H2O+CO2

(2)

经过上述反应，烟气中的SO2被脱除，生成了副产物石膏。整体的工艺流程如图1所示。

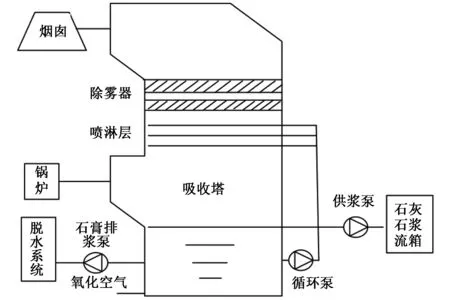
图1 石灰石-石膏湿法脱硫系统工艺流程图Fig. 1 Process flow chart of limestone-gypsum wet desulfurization system

2 数据预处理与相关性分析

2.1 数据预处理

数据预处理是建模的关键步骤，在实际数据的采集过程中，往往因为设备老化，通信故障等问题造成数据跳变或者短暂缺失，根据对脱硫系统的经验，对于每个测量值发生跳变或缺失的数据进行删除处理，保证数据集的有效性。

2.2 相关性分析

2.2.1 皮尔逊相关系数

脱硫系统中影响出口SO2浓度的因素有很多，建模过程中输入维数过大会导致模型的效率下降，为了降低输入的维度，需要寻找对因变量最具有强解释力的自变量集合[9]，相关性分析可以定量衡量自变量与因变量的密切关系，可以通过自变量的选择来提高模型的解释性和预测精度。目前使用较多的相关性分析方法主要有互信息、相关系数、协方差等，为了找到自变量集合的最优解，本文使用皮尔逊相关系数进行变量的选取。皮尔逊相关系数定义为

(3)

(4)

(5)

(6)

2.2.2 分析结果

使用皮尔逊相关系数对影响脱硫出口SO2浓度的因素进行相关性分析，根据相关性的强弱筛选得到6组相关性最强的主要变量，筛选后的变量及波动范围如表1所示。

表1 影响出口浓度的因素与波动范围Tab.1 Influencing factors and fluctuation range of outlet concentration

浆液循环泵运行台数的多少直接影响了相同工况下出口的浓度，但由于浆液循环泵投运台数只有3个固定值，作为拟合的参数意义不大，考虑分情况进行讨论，本文以4台泵投运为例，建立出口SO2的预测模型。

3 基于Lasso算法的预测模型

3.1 Lasso回归算法

对于出口SO2浓度Y和选定的参数X=(x1,x2,…,xn),假定模型为线性模型，则其具体的表达式可以写为

Y=λ1×x1+λ2×x2+…+λn×xn+β

(7)

式中：λ为回归系数；β为整体的误差。

在回归模型中，为了保证拟合的效果，一般要求损失函数RRS最小，设损失函数为

(8)

Lasso回归算法 (Least absolute shrinkage and selection operator)是一种压缩估计。它通过构造一个罚函数得到一个较为精炼的模型[11]，基本思想是在回归系数的绝对值之和小于一个常数的约束条件下，使残差平方和最小化，从而能够产生某些严格等于0 的回归系数[12]，得到可以解释的模型。具体的计算公式为

(9)

式中：X=(x1,x2,…,xn)T是数据矩阵即通过变量筛选后模型的输入，Y=(y1,y2,…,yn)T是由标签组成的列向量即预测模型的输出，w为系数矩阵。

对于w的求解，采用坐标下降法，通过启发式的方式进行迭代求解函数的最小值。首先设定初值w(0)，括号里的数表示迭代轮数。在第k轮迭代中，w的n个维度的迭代公式为

(10)

(11)

…

(12)

如果w(k)和w(k-1)在各维度上变化都足够小，那么w(k)即为所求，否则继续进行下一轮迭代。

由于Lasso算法也属于线性算法范畴，用单纯的一次项进行拟合会导致模型复杂度不够，预测精度不足，为了进一步提升预测精度，选取各参数最优的函数形式来代替，最终得到的预测模型为

Y=λ1×h(x1)+λ2×h(x2)+…+λn×h(xn)+β

(13)

式中：h(x)为各参数最优的函数表达式，包括线性函数h(x)=k×x+c，二次多项式函数h(x)=a×x2+b×x+c，幂函数h(x)=a×xb等。

3.2 函数形式的选取

3.2.1 粒子群优化算法

粒子群优化算法(PSO)是通过模拟鸟类觅食行为而提出的一种群体智能搜索算法。算法采用速度—位置搜索模型。每个粒子代表解空间的一个候选解，解的优劣程度由适应度函数决定，而适应度函数根据优化目标定义。

PSO算法随机初始化一群粒子，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己[13]。一个是粒子本身所找到的最优解，即个体极值pbest；，另一个是整个种群目前找到的最优解，称之为全局极值gbest。具体的算法步骤如图2所示。

图2 PSO算法计算步骤Fig. 2 PSO algorithm calculation steps

3.2.2 函数形式筛选

假设各参数相互独立，使用粒子群优化算法对每一项参数以不同的函数形式进行拟合，对比其与出口SO2浓度的误差，找到最优的函数形式。经过对比，拟采用线性、二次多项式、三次多项式、幂函数4种结构进行拟合。以SO2脱除量为例，最优的拟合结果如图3所示。

评价函数使用均方差表示，具体形式为

(14)

式中：r为拟合出的数学期望；N为样本个数。

图3 多项式函数拟合效果Fig. 3 Fitting effect of polynomial function

分别分析4种函数形式并计算相应的误差，其结果如表2所示。

表2 不同函数形式拟合结果Tab.2 Fitting results of different functional forms

由表2可知，最优的函数形式为二次多项式，具体的表达式为

f(x)=1.742e-6x2±0.02x+68.84

(15)

式中：x为SO2脱除量；f(x)为函数计算得到的出口SO2浓度。对剩余参数使用同样的方法寻找最优的函数形式。具体结果如表3所示。

表3 参数最优的函数形式Tab.3 Function form with optimal parameters

4 模型评估

4.1 选取训练数据

在实际现场运行数据中选取工况较为稳定的256组数据，其中机组负荷数据如图4所示。可以发现机组负荷波动较大，数据的区间也分布不均，350 MW以下的时刻较多，只有个别时刻在400 MW以上，直接使用这种分布不均的数据作为训练集会导致模型预测精度的偏移，训练样本多的区间预测的结果更加准确，样本少的会有较大误差。