基于功率特征分组的空时自适应脉冲干扰抑制方法
2022-02-18高文宁
刘 鹏,王 盾,高文宁
(航天恒星科技有限公司,北京 100095)
0 引言
随着导航电子对抗技术的发展,军用导航接收机面临着越来越多的电磁干扰。由于卫星导航信号到达地面时极其微弱,仅靠信号本身的扩频增益无法保证接收机在强干扰环境下正常工作,必须借助其他的抗干扰措施。
脉冲干扰是一种常见的干扰类型,由持续时间短、信号幅度大的不规则脉冲或噪声尖峰组成,通常具有较宽的频谱。按照产生机理,脉冲干扰可分为两类,一类是由于大气中的雷暴现象等产生的自然干扰;一类是由高频电子设备如继电器、雷达、干扰源等产生的人为干扰。其中L频段雷达和L频段的脉冲干扰源极易对导航信号产生影响。
由于脉冲干扰的高带宽、突发性等特点,脉冲干扰抑制具有较大难度。针对脉冲干扰的抑制,主要有时域、频域、空域以及多域联合滤波算法。其中,时域、频域滤波算法主要针对窄带干扰,而脉冲干扰通常占据较宽的频带,因此,时域、频域滤波算法对脉冲干扰的抑制效果会变差或失效。虽然脉冲消隐(Pulse Blanking)方法对干扰带宽不敏感,但仍然会造成信号能量的损失。阵列信号处理算法主要包含空域自适应处理(Spatial Adaptive Processing,SAP)、空时自适应处理(Space-Time Adaptive Proces-sing,STAP)以及空频自适应处理(Space-Frequency Adaptive Processing,SFAP)等类型,具有更强的抗干扰能力以及更小的信号衰减,在卫星导航接收机的研制过程中得到了广泛应用。阵列信号处理滤波权值的求取方法主要包括块处理算法和连续处理算法两种,块处理算法为无反馈开环处理,权值计算无收敛过程,因此得到了大量应用。然而,常规的阵列信号块处理算法通常假设干扰的统计特征是平稳的,利用当前的信号采样数据计算滤波权值,对当前和后续采样数据进行干扰抑制。一方面,由于脉冲干扰的突发性,当计算滤波权值的数据块中不包含脉冲干扰,而脉冲干扰恰好出现在后续数据中时,将无法对脉冲干扰进行有效抑制;另一方面,即使计算滤波权值的数据块中包含脉冲干扰,由于可能仅是一部分时段的信号采样数据包含了脉冲干扰,据此计算的干扰零陷深度也会受到影响,从而影响算法的抗干扰能力。
针对以上问题,本文通过功率检测对接收数据进行分组,改进常规空时自适应处理算法,提升其对脉冲干扰的抑制能力。首先,对接收数据进行功率检测,判断当前信号采样数据块是否包含干扰;其次,根据检测结果将数据块进行分组,分为有干扰数据组和无干扰数据组;随后,利用有干扰数据组计算滤波权值,滤除其中的干扰信号,对于无干扰数据组,则将滤波权值固定为常数,保留其中的有效信号成分;最后将滤波后的两组数据按照采样顺序重新进行合并输出。通过数据分组,提高了干噪比的统计计算准确度,增加了干扰零陷深度,从而实现了抗干扰能力的提升。
本文结构如下:第1节介绍常规空时自适应处理算法,并分析其在脉冲干扰抑制中存在的问题;第2节提出功率特征分组空时自适应处理方法,并分析其对脉冲干扰抑制性能的提升;第3节对本文提出的方法与常规算法进行仿真分析及性能对比;第4节为结论。
1 常规空时自适应处理算法及存在问题
1.1 常规空时自适应处理算法概述
空时自适应处理的结构框图如图1所示,阵列包含个天线单元,每个单元后有-1个时间延迟线,则STAP接收数据模型可表示为

图1 空时自适应处理框图Fig.1 Space-time adaptive processing block diagram
()=()+()+()
(1)
其中,=[,…,1,,…,2,…,1,…,]为×1空时数据向量,上标T表示向量转置;()为导航信号复包络向量,()=[(),(),…,()],()为第个导航信号的复包络;为信号阵列空时流形矩阵,=[1,2,…,],为第个导航信号的空时导向矢量;()为干扰复包络向量,()=[(),(),…,()],()为第个干扰的复包络;为干扰阵列空时流形矩阵,=[1,2,…,],为第个干扰的空时导向矢量;()为阵列噪声向量。
阵列的协方差矩阵定义为
=E[()()]
(2)
式中,E[·]表示求期望值,上标H表示向量共轭转置。
空时自适应处理的滤波权值为
=μ
(3)
其中,为常数;为约束矢量。
则经空时自适应处理后的输出为

(4)
1.2 脉冲干扰抑制问题分析
假设脉冲干扰为一个时间连续的带内干扰与占空比为1(>1)的周期矩形脉冲的乘积,干扰表示为

(5)
式中,()为时间连续干扰的复包络;()为持续时间为、占空比为1的矩形脉冲,表示为

(6)
当天线阵列接收到式(5)所示的一个干扰时,并假设信号、干扰与噪声不相关,则协方差矩阵为
=E[()()]

(7)
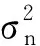
由式(5)得

(8)

由于信号功率远低于干扰和噪声功率,综合式(7)、式(8)并将信号分量省略,得

(9)
对协方差矩阵进行特征值分解,得
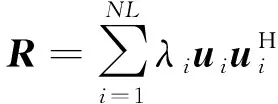
(10)
将特征值按照从大到小的顺序排列,由式(9)、式(10)得

(11)
其中,为干扰特征值;为干扰特征向量;其余为噪声特征值和噪声特征向量。干扰方向的阵列响应为




(12)
其中

(13)
由式(11)和式(12),当干扰功率远大于噪声功率时

(14)
由上述分析可见,空时自适应处理的干扰抑制能力与干扰特征值成正比,干扰特征值越大,零陷越深,干扰抑制能力越强。常规空时自适应处理算法未对有干扰数据和无干扰数据进行区分,统一进行协方差矩阵估计及权值计算。一方面,由式(11),干扰特征值与脉冲干扰的占空比成正比,当脉冲占空比较低时,将导致零陷深度降低,抗干扰能力下降;另一方面,在工程实现过程中,用于协方差矩阵估计的数据是有限的,当脉冲占空比降低到一定程度后,将出现用于协方差矩阵估计的数据不包含干扰的情况,此时如果利用当前数据块计算的权值对后续数据进行干扰抑制,甚至会出现抗干扰失效的问题。
2 功率特征分组空时自适应处理方法
2.1 方法描述
针对以上问题,本文提出了一种基于功率特征分组的空时自适应处理方法,以提高对脉冲干扰的抑制能力。
该方法的实现步骤如下:
步骤一:对输入数据进行功率检测,根据检测结果将数据分为两组,即有干扰数据和无干扰数据,两组数据分别表示为

(15)
干扰检测的阈值需要在虚警概率和漏警概率之间进行折中,本文的阈值设为噪声功率增加3dB。
步骤二:将数据进行分组后,分别计算两组数据的滤波权值。第一组数据包含干扰,权值计算包含协方差矩阵估计和逆矩阵与约束向量相乘2个过程。

(16)

(17)
实现过程中,需要缓存一段数据并利用有限采样点对协方差矩阵进行估计,在数据缓存段内采样点可以跨周期。当脉冲干扰占空比较小,缓存的数据点数不足时,则考虑减少统计点数或增加第二组的数据采样点。
第二组数据无干扰,但为了保证滤波延迟的一致性,仍然对第二组数据进行滤波处理,其滤波权值为

(18)
步骤三:利用权值对分组数据进行自适应滤波
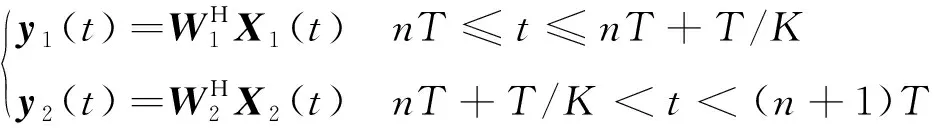
(19)
步骤四:将滤波后的分组数据合并输出

(20)
2.2 抗干扰性能分析
数据分组后,只有第一组数据存在干扰,因此对第一组数据的抗干扰性能进行分析。
由式(15)、式(16)得

(21)
1为干扰期望功率,其值为

(22)
省略导航信号分量,协方差矩阵为

(23)
对进行特征值分解,得

(24)
将特征值按照从大到小的顺序排列,由式(23)、式(24)得
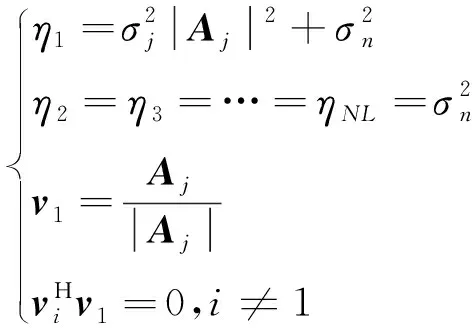
(25)
其中,为干扰特征值;为干扰特征向量;其余为噪声特征值和噪声特征向量。干扰方向的阵列响应为
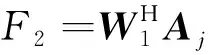



(26)
其中

(27)
由式(25)和式(26),当干扰功率远大于噪声功率时

(28)
由式(14)和式(28),本文提出的算法在进行自适应滤波后,干扰方向在相应频带的阵列响应幅值更低,可获得更深的干扰零陷,因此具有更强的抗干扰能力,性能提升增益值为

(29)
需要说明的是,式(29)是算法的期望增益,实际增益需要具体分析,分析极限情况可见:
1)当趋近于1,即脉冲干扰占空比趋近于100%,脉冲干扰趋近于时间连续干扰时,性能提升增益值趋近于0;而当=1时,干扰已经变为时间连续干扰,所有数据均在分组1,此时改进算法的处理过程与常规算法相同,而算法性能增益为0。上述结果与式(29)相符。
2)当趋近于无穷大,即脉冲干扰占空比趋近于0时,由于仅有极少的数据在分组1,此时计算协方差矩阵需要减少统计点数或增加第二组的数据采样点,因此实际增益值会低于期望值。
3 仿真实验
导航信号中心频率设置为BDS B3频点,阵列为四阵元方阵,天线单元间距为半波长。信号下变频后的模拟中心频率为15.48MHz,采样频率为62MHz。空时自适应处理每个天线阵子后采用3个时域抽头,协方差矩阵估计点数为4096,权值计算采用自适应调零算法。
接收导航信号的信噪比设置为-25dB,并施加1个脉冲干扰,干扰来向为方位角120°、俯仰角45°。由于实际抗干扰测试通常设置脉冲周期为10μs~100μs,为便于分析,本文将脉冲干扰的1个周期设置为对应4096个采样点,即脉冲周期约为66μs,并将脉冲干扰占空比设置为25%。则采用常规空时自适应处理时,1次协方差矩阵估计对应1个脉冲干扰周期。而采用本文提出的改进算法,当对完成分组后的有干扰数据进行协方差矩阵估计时,1次估计需要用到4个脉冲干扰周期的数据。
对协方差矩阵进行特征值分解,最大的特征值为干扰特征值,其余特征值为噪声特征值。由于噪声特征值基本稳定,因此可以用干扰特征值和噪声特征值的比值(INR)来表征干扰特征值的变化趋势。设置干信比(ISR)从60dB逐渐增大到100dB,由特征分解得到的两种算法的干噪比如图2所示,干扰方向的阵列响应幅值如图3所示。

图2 干扰特征值分析Fig.2 Interference eigenvalue analysis

图3 干扰方向阵列响应幅值Fig.3 Array response magnitude in the interference direction
可见,当脉冲干扰占空比为25%时,本文算法的干扰特征值相比原算法增加约6dB,干扰方向的阵列响应幅值降低约6dB,即零陷深度增加约6dB,仿真结果与理论分析一致。
将方位角固定为干扰方位角,当干信比分别为70dB、80dB、90dB和100dB时,两种算法的阵列响应幅值随俯仰角的变化情况如图4所示。由图4可见,两种算法均能在干扰方向形成明显的零陷,但相比常规空时自适应处理,本文方法的零陷深度更低,在不同干信比条件下相比原算法均增加约6dB。

(a)干信比70dB
4 结论
本文对常规空时自适应处理算法进行了介绍,分析了常规算法在脉冲干扰抑制中存在的问题,在此基础上,提出了一种基于功率特征分组的空时自适应处理方法,并对该方法的性能进行了理论和数据仿真分析,结果表明:
1)通过功率检测将采样数据进行分组处理,可提升接收脉冲干扰时干噪比的统计计算准确度,增加干扰零陷深度,实现抗干扰能力的提升。
2)常规算法和本文算法的性能分析结果表明,本文算法的性能提升期望增益值与脉冲干扰的占空比倒数成正比。
3)仿真结果与理论分析一致,证明了该方法的有效性。同时,本文所提算法与常规空时自适应处理算法相比,处理复杂度基本一致,具有较强的工程应用价值。
