一种基于参数控制的低轨星载接收机载波跟踪算法

2022-02-18檀晓萌罗瑞丹

导航定位与授时 2022年1期

檀晓萌, 罗瑞丹, 徐颖, 苏中, 袁超

(1.北京信息科技大学自动化学院高动态导航技术北京市重点实验室，北京 100101；2.中国科学院空天信息创新研究院，北京 100094)

0 引言

随着卫星导航系统(Global Navigation Satelli-te System，GNSS)的现代化升级与组网完善，星载自主导航接收机作为空间航天器必备载荷，能够为航天器提供高精度、高可用、实时连续的定轨、测姿、授时等信息，极大地提高了航天器运行自主性，对于保障航天任务具有十分重要的意义。

低轨(Low Earth Orbit，LEO)卫星因其特有的平台优势，成为支撑大气探测、海洋测高、重力场模型精化等科学探测任务的重要平台，对应LEO星载导航接收机研制也成为未来导航研究与低轨定轨的重要研究方向。同时，LEO卫星因其轨道和任务特性，使得其建设向着平台体积集约化、星座规模巨型化、功能任务复合化、业务服务精细化等方向发展，这也要求LEO星载接收机在低功耗、高精度等方面具备明显的性能优势。

但是LEO卫星运行速度可达每秒数千米，为星载接收机引入大多普勒频移与频繁快速换星等设计难题。特别地，对接收机载波跟踪环路提出了较高的动态适应性和跟踪精度要求，同时基于星上资源和实现复杂度考虑，载波跟踪环路设计也不宜过度复杂。

目前，国内外针对LEO星载接收机跟踪环路的设计算法，从原理上可以分为三大类：1)基于经典环路辅助/组合的载波环，如锁频环(Frequency-Locked Loop，FLL)辅助锁相环(Phase-Locked Loop，PLL)。FLL辅助PLL结构中通过FLL和PLL之间的切换，用FLL进行大频偏的辅助捕捉，PLL进行精确跟踪，其结构较为简单，但环路参数的确定比较困难，在星载环境下，切换机制导致的环路稳定性下降更为明显。2)基于惯导辅助的载波环，通过速率辅助去掉大部分动态，实现高精度跟踪，但惯导系统造价高昂、结构复杂，导致其在星载环境下应用受限。3)基于参数估计理论的载波环，如最大似然估计载波环、卡尔曼滤波/扩展卡尔曼滤波/无迹卡尔曼滤波载波环、粒子滤波/无迹粒子滤波载波环等。这类算法将信号过程看作系统输入白噪声的过程，自适应地调整环路参数，但只适应于特定的系统，算法鲁棒性较差，且运算量较高，不易于在资源受限的星载接收机上进行工程实现。

针对低轨星载接收机引入大多普勒频移问题及频繁快速换星需求，传统载波跟踪算法(锁相环)无法兼顾跟踪精度与收敛速度，因此，本文提出了一种基于参数控制的载波跟踪环路(Parameter Control Factor Phase-Locked Loop，PCF-PLL)。该环路将环路滤波器分为牵引滤波器和跟踪滤波器两种状态，通过参数控制因子实现两滤波器的协同配合，有效地解决了大多普勒频移问题，实现了环路快速入锁，提高了环路跟踪精度和鲁棒性；同时将更多的多普勒频移引入载波跟踪环处理，可降低捕获环节的计算量和复杂度，提高星载接收机整体的工作效率，环路设计简单，有利于硬件实现。

1 GNSS-LEO信号多普勒特性分析

GNSS-LEO信号为基于LEO星载平台观测接收到的GNSS信号，其信号多普勒频移是由GNSS卫星与LEO卫星之间的相对运动引起的，LEO卫星速度、GNSS卫星速度在GNSS-LEO直线距离上的投影之和直接影响信号多普勒频移大小，LEO卫星与GNSS卫星的位置如图1所示。

图1 LEO与GNSS卫星相对位置示意图Fig.1 The relative position of LEO and GNSS

多普勒频移可表示为

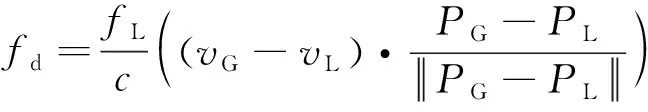
(1)

式中

(2)

(3)

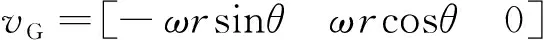
(4)

(5)

式中：为GNSS-LEO信号多普勒频移；为GNSS-LEO信号载波频率；为光速；、为GNSS、LEO卫星的位置；、为GNSS、LEO卫星的速度；、为LEO、GNSS的轨道半径；、为LEO、GNSS的角速度；为GNSS轨道与LEO轨道之间的倾角；为LEO卫星位置与轴夹角；为GNSS卫星位置与轴夹角。

由上述公式可知，GNSS-LEO信号多普勒特性与卫星的位置、速度等运动状态密切相关，两卫星速度在两者直线距离方向上的投影和越大，多普勒频移越大。卫星的运动状态直接与其轨道高度有关，目前低轨卫星的轨道高度一般为120～2000km，故本文选取LEO轨道高度为500km，基于STK进行仿真，得到GNSS-LEO信号多普勒频移及其相关特性如表1所示。

表1 GNSS-LEO信号的多普勒频移参数

由表1可得，GNSS-LEO信号载波多普勒频移最大值为45kHz左右，多普勒频移变化率最大值不超过70Hz/s，多普勒加速率范围为[0Hz/s～0.2Hz/s]。所有GNSS-LEO信号数据的最大多普勒频移对应的高度角都较低，在0°左右，即最大多普勒频移发生在GNSS-LEO之间刚可见或即将不见的时刻；而最大多普勒频移变化率对应的高度角多数偏高，主要是因为最大多普勒频移变化率发生在GNSS卫星过顶LEO卫星时刻。

选取LEO-GPS01信号最大多普勒频移最大的一组数据作为接收机载波跟踪环路的输入信号，其载波多普勒、多普勒频移变化率及多普勒加速率如图2所示,载波多普勒、多普勒频移变化率与GPS高度角如图3所示。

由图2可得，LEO-GPS01信号载波多普勒频移可达40kHz，载波多普勒变化率最大不超过60Hz/s，载波多普勒加速率范围为[0Hz/s～0.15Hz/s]，基本可视为0。由图3可得，LEO-GPS01信号最大多普勒频移发生时，对应GPS高度角在-5°～-10°之间；而最大多普勒频移变化率对应的GPS高度角为45°左右。

图2 LEO-GPS01载波多普勒信息图Fig.2 Carrier Doppler of LEO-GPS01 signal

图3 LEO-GPS01载波多普勒信息与高度角Fig.3 Carrier Doppler and GPS altitude angle of LEO-GPS01 signal

由表1可知，低轨星载接收机的高动态环境主要表现为大的多普勒频移、不高的多普勒频移变化率和可忽略不计的多普勒加速率。同时，GNSS-LEO可见持续时间较短，平均为47min左右，且为保证精细观测，需要频繁换星，这对星上接收机的处理速度及跟踪精度要求更高。

2 PCF-PLL

针对在GNSS-LEO信号跟踪中引入大多普勒频移导致入锁慢、接收机处理难度及复杂度较大的问题，本文提出了一种PCF-PLL。该环路将环路滤波器状态分为牵引和跟踪两阶段，引入参数控制因子调整滤波器状态，从而达到快速入锁、精确稳定跟踪且不增加环路复杂度的目的。

2.1 PCF-PLL算法原理

为使接收机在动态环境下具有较高的鲁棒性，最有效的方法之一就是增加环路带宽。PCF-PLL算法基于此，将环路滤波器分为两种状态：1)牵引滤波器，主要实现牵引信号快速入锁的功能；2)跟踪滤波器，主要实现精确跟踪信号的功能。为降低环路参数设计复杂度，通过参数控制因子实现牵引滤波器和跟踪滤波器的协同工作，简单易行地完成接收机高动态稳定跟踪。PCF-PLL算法原理如图4所示，图4(a)为PCF-PLL环路框图，图4(b)为PCF-PLL牵引滤波器框图，图4(c)为PCF-PLL跟踪滤波器框图。

如图4(a)所示，PCF-PLL的传递函数表达式为

(a) PCF-PLL环路框图

(6)

式中：()为环路滤波器传递函数；为环路增益，表达式为

(7)

式中：、分别为鉴相器和数控振荡器的增益。

从而可得PCF-PLL的误差传递函数表达式为

(8)

如图4(b)所示，PCF-PLL牵引滤波器的传递函数可表述为

(9)

式中：为阻尼系数；为参数控制因子；′为牵引阶段环路的特征频率。

将式(9)代入式(6)和式(8)可得PCF-PLL牵引阶段传递函数及误差传递函数为

(10)

(11)

同理，如图4(c)所示，PCF-PLL跟踪滤波器的传递函数、跟踪阶段传递函数及误差传递函数分别为

(12)

(13)

(14)

为简化PCF-PLL分析，对两阶段的传递函数和误差函数进行规范化，引入一个参数控制因子，其表达式为

′=

(15)

由式(15)可得，参数控制因子可建立牵引滤波器和跟踪滤波器之间的关系，使2个独立的滤波器参数实现协同调整，降低环路复杂度。当参数控制因子≤1时，误差传递函数值减小，环路滤波器即跟踪滤波器,对应环路跟踪阶段；反之，为牵引滤波器，对应环路牵引阶段。

则PCF-PLL环路传递函数及误差传递函数为

(16)

(17)

根据式(13)可推导PCF-PLL环路带宽公式为

(18)

由式(18)可知，环路带宽与参数控制因子成正比。故可通过调整参数控制因子，调整接收机灵敏度及测距精度。

为保证环路整体计算量较小，本文采用计算量更小的鉴相器，其表达式为

()=

(19)

式中：()和()分别为时刻同相支路和正交支路的相关输出结果；sign(·)为符号函数。

由图4(a)可得，鉴相器与环路滤波器之间存在一个切换点，用来切换环路滤波器的状态，从而控制整个环路的状态。当接收机首次启动或出现GPS信号丢失、失锁时，载波跟踪环路首先进入PCF-PLL牵引阶段，通过牵引滤波器的牵引作用快速缩小信号频差范围，实现快速入锁、持续稳定跟踪；当信号频差范围缩小至PLL可跟踪时，环路滤波器切换为跟踪滤波器，实现精确跟踪。

通过上述分析可得，PCF-PLL引入的参数控制因子不仅实现了牵引滤波器与跟踪滤波器的协同配合，且与环路带宽直接相关，可通过调整接收机灵敏度及跟踪精度，提高PCF-PLL在高动态环境下的鲁棒性。此外，PCF-PLL还采用了计算量更小的鉴相器，使得整个环路的计算量及复杂度与PLL相当。

2.2 PCF-PLL性能推导

本文基于PCF-PLL算法原理，推导了参数控制因子与环路的收敛速度及跟踪误差之间的表达式，给PCF-PLL参数优化提供了理论依据。

2.2.1 PCF-PLL收敛速度

接收机的收敛速度一般定义为环路起始的误差响应幅值衰减至其1/4所需的时间，用收敛时间来表示。通过推导环路误差响应幅值公式，可得收敛时间的表达式。

环路误差响应幅值与输入信号的类型有关。当输入信号()包含相位阶跃信号、频率阶跃信号及频率斜升信号时，如下

(20)

式中：为频率斜升值；为频率阶跃值；为相位阶跃值；()为单位阶跃序列。

此时，PCF-PLL误差响应()为

(21)

可得收敛时间的表达式为

(22)

由式(22)可得，环路的收敛时间与参数控制因子成反比。通过增大参数控制因子，可达到缩短收敛时间、提高收敛速度的目的。

2.2.2 PCF-PLL跟踪误差

由PLL的跟踪误差公式可推导得出PCF-PLL的3跟踪误差表达式为

3=3+

(23)

式中，为输入信号的载噪比；为相干积分时间；为载波L1的波长；为卫星和接收机的连线距离。

由式(23)可得，环路跟踪误差主要跟环路的热噪声误差有关。通过控制参数控制因子可有效地控制环路跟踪误差，减小参数控制因子，环路跟踪误差随之降低。

由上述分析可得，当参数控制因子>1时，PCF-PLL的跟踪误差及收敛速度都优于PLL；参数控制因子与环路收敛速度正相关，与环路跟踪误差正相关。环路最优参数控制因子的选择应满足保证跟踪精度的前提下，使收敛速度尽可能快。下面将详细分析参数控制因子最优值的选择。

2.3 PCF-PLL参数控制因子κ最优值的选择

环路跟踪误差为环路性能评估的首要指标，故在选择参数控制因子时，首先考虑其约束作用。为选择一个合适的参数控制因子，将分析不同载噪比下，参数控制因子与环路跟踪误差的关系。

参数控制因子的选择首先要满足环路跟踪误差小于跟踪门限，对环路跟踪门限的保守估计为环路3跟踪误差小于其1/4鉴相牵入范围(90°)，即

3<225°

(24)

不同载噪比及动态多普勒下，环路误差特性曲线如图5所示。

图5 不同载噪比C/N0及动态多普勒下误差特性曲线Fig.5 Error characteristics under different carrier-to-noise C/N0 and dynamic Doppler

由图5可得，载噪比与参数控制因子范围对应关系如表2所示。

表2 载噪比与参数控制因子

由图5和表2可得，随着载噪比的降低，环路参数控制因子的范围越来越小。当信号载噪比降至35dBHz时，参数控制因子已不能优化环路性能。

由以上分析可得，参数控制因子的增大，虽会造成跟踪误差的增大，但可以很好地消除高动态引起的误差以及缩短跟踪高动态信号时环路收敛的时间。故而当高动态应力较小时，参数控制因子值应尽可能小；反之，当高动态应力较大时，参数控制因子值应尽可能大。

3 仿真校验

本节将仿真验证PCF-PLL对GNSS-LEO信号跟踪的有效性，并从环路跟踪误差和环路收敛时间两方面评估PCF-PLL性能，同时验证理论推导的PCF-PLL参数控制因子最优取值区间。环路基本仿真参数如表3所示。

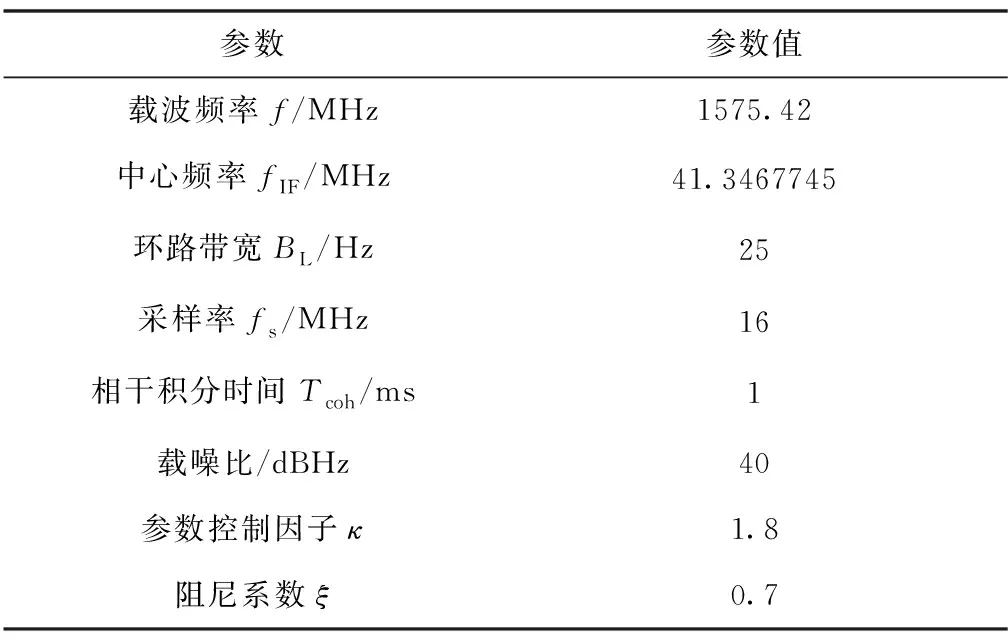
表3 PCF-PLL仿真参数

3.1 PCF-PLL有效性验证

通过对PCF-PLL整个可见周期及前1500ms跟踪误差的仿真实验，评估PCF-PLL的有效性。为此，设置了2组实验：1)选取LEO-GPS01的一次可见周期进行仿真分析，评估其跟踪稳定性和鲁棒性，其输入信号存在动态多普勒信息，最大多普勒频移可达40kHz，载波多普勒变化率最大不超过60Hz/s，载波多普勒加速率范围为[0Hz/s～0.15Hz/s]；2)取第一组实验前1500ms数据，在不同环路带宽(25Hz/15Hz)下进行仿真分析，评估其跟踪收敛时间和跟踪精度，其输入信号动态特性同1)。实验1)的载波频率跟踪误差曲线如图6所示。

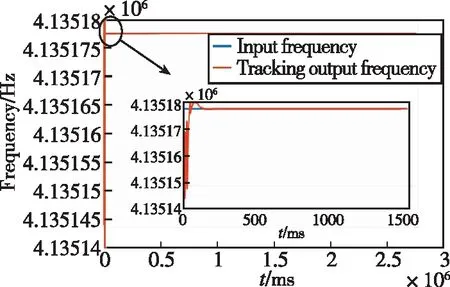
图6 PCF-PLL频率跟踪误差Fig.6 Tracking error of PCF-PLL frequency

由图6可得，PCF-PLL在整个可见周期内，能够稳定跟踪含动态多普勒信息的GNSS-LEO信号，证明了PCF-PLL的跟踪稳定性；且从跟踪结果来看，由参数控制因子决定的环路状态切换机制并未引起跟踪上的较大波动，证明了PCF-PLL的鲁棒性。综合来看，PCF-PLL可实现大多普勒频移跟踪、快速入锁，跟踪精度较好。

整个可见周期前1500ms内，PCF-PLL跟踪阶段环路带宽和PLL环路带宽均为25Hz，参数控制因子为1.8时，PCF-PLL与PLL跟踪结果如图7所示。

图7 PCF-PLL与PLL跟踪相位差Fig.7 Tracking phase error between PCF-PLL and PLL

从图7中可以看出，当PCF-PLL跟踪阶段环路带宽和PLL环路带宽均为25Hz时，PLL虽然也能在1500ms内跟踪上输入信号，但其入锁时间过长，超过500ms，影响了接收机的即时性；而PCF-PLL能极大地缩短入锁时间，降至110ms以内，且跟踪精度不亚于二阶锁相环。

整个可见周期前1500ms内，PCF-PLL跟踪阶段环路带宽和PLL环路带宽均为15Hz，参数控制因子为1.8时，PCF-PLL与PLL前1500ms跟踪结果如图8所示。

图8 PCF-PLL与PLL跟踪相位差Fig.8 Tracking phase error between PCF-PLL and PLL

从图8中可以看出，当PCF-PLL跟踪阶段环路带宽和PLL环路带宽均为15Hz时，PLL不能在1500ms内跟踪上输入信号，入锁困难；而PCF-PLL能实现1500ms内入锁，且跟踪误差小。

GNSS-LEO可见时间短，可见次数多，故星载接收机在捕获、跟踪中需要频繁换星，且信号伴随动态多普勒频移，其对即时、稳定跟踪要求更高。而PLL在这种状况下，存在入锁困难、失锁后重新入锁的时间较长等问题，显然是无法满足要求的。PCF-PLL则通过一个简单的切换机制及时调整环路状态，很好地解决了这个问题。

3.2 PCF-PLL参数优化仿真分析

通过对不同信噪比下环路收敛时间进行仿真分析，进一步验证了PCF-PLL参数控制因子优化策略，并对其进行了修正。由前面的理论分析可知，参数控制因子与信号动态性能和跟踪误差要求有关。通过对不同参数控制因子的仿真分析，验证了理论部分对参数控制因子的优化策略的有效性。设置PCF-PLL跟踪阶段环路带宽和PLL环路带宽均为25Hz，参数控制因子与牵引阶段环路带宽的对应关系，如表4所示。

表4 参数控制因子κ与环路带宽

根据表4数据，仿真得到PCF-PLL不同参数控制因子下的跟踪误差曲线，如图9所示。

图9 PCF-PLL不同参数控制因子κ下跟踪相位误差Fig.9 Tracking phase error under different PCF-PLL parameters

从图9中可以看出，在参数控制因子理论最优范围[1, 2.6]内，随着参数控制因子的增大，环路收敛时间加快100～200ms，可实现快速入锁，且跟踪误差均较小;但参数控制因子越大，环路带宽越大，牵引阶段环路引入的噪声越多，牵引阶段的信噪比SNR下降越严重。可见，参数控制因子的选择要权衡收敛速度和信噪比SNR。

为保证信号质量，优化环路性能，加入收敛时间作为约束条件，进一步优化参数控制因子的最优范围。仿真得到不同参数控制因子下PCF-PLL收敛时间与参数控制因子的特性曲线，如图10所示。

图10 参数控制因子κ与收敛时间trFig.10 PCF κ and convergence time tr

由图10可得，随着参数控制因子的增大，收敛时间总体呈下降趋势，但存在一定起伏波动，可分为6个阶段，依次为图10中标示的A、B、C、D、E、F。各阶段参数控制因子对应的牵引阶段环路带宽及收敛时间如表5所示。

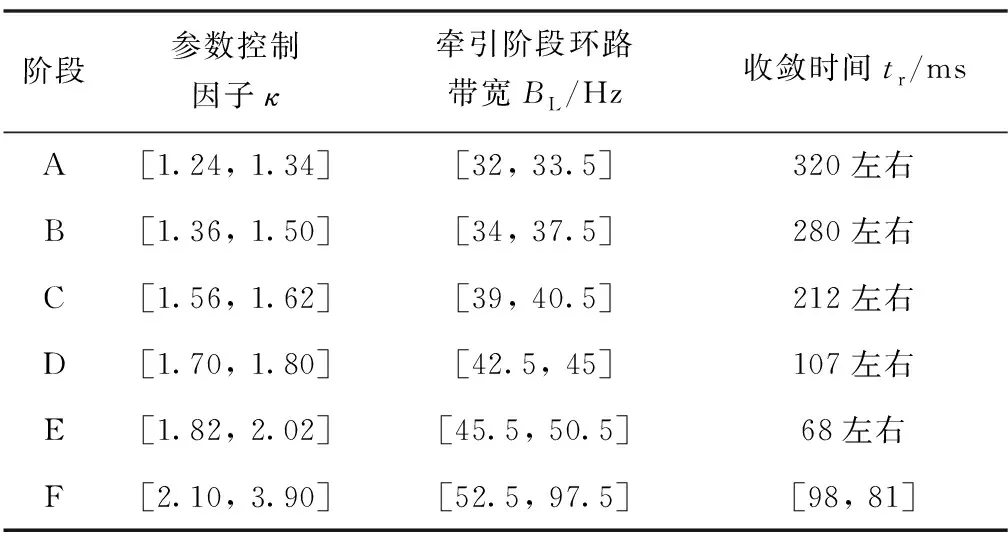
表5 各阶段参数表

由图10和表5可得，参数控制因子在收敛速度和信噪比的权衡中存在一个最优阶段，即E阶段，此时收敛速度最快，信噪比为0.8dB左右，且满足跟踪门限的要求。此后，增大参数控制因子对于缩小环路收敛时间的控制效果已不显著。

由上述分析可知，在低轨星载的高动态环境下，PCF-PLL环路带宽为25Hz、相干积分时间为1ms时，参数控制因子的最优范围为[1.82, 2.02]，可跟踪信号最低至35dBHz;而三阶锁相环环路带宽为18Hz、相干积分时间为1ms时，环路最低跟踪信号约为35dBHz，与PCF-PLL相当。综上所述，采用PCF-PLL可提高PLL的动态适应能力，其入锁时间可缩短78%，环路收敛速度更快，在保证跟踪精度的同时，提高了环路对于低信噪比跟踪信号的跟踪能力，且环路阶数低，有利于硬件实现。