陆战对抗中的智能体博弈策略生成方法
2022-02-17王玉宾孙怡峰张玉臣
王玉宾 孙怡峰 吴 疆 李 智 张玉臣
1.中国人民解放军战略支援部队信息工程大学 河南 郑州 450001
智能体是人工智能的一个基本术语, 广义的智能体包括人类、机器人、软件程序等[1]. 狭义的智能体是能感知环境, 根据环境变化作出合理判断和行动, 从而实现某些目标的计算机程序. 从感知序列集合到执行动作集合的映射也称为智能体的策略[2]. 智能体策略的研究对实现无人系统自主能力[3]和人机混合智能[4]具有重要意义.
决策指根据一定目标选择备选方案或动作的过程. 传统使用脚本规则[5]、有限状态机[6]、行为树[7]等方法进行智能体决策行为建模, 决策模型对应了智能体的策略. 这类智能体的策略具有较强的可解释性, 但是其需要大量的领域专家知识. 另一方面上述智能体通常使用基于专家知识的纯策略, 其行为模式是固定的, 在复杂对抗场景中存在适应性不强和灵活度不够的问题. 近年, 深度强化学习成为智能体策略生成的重要方法, 在Atari 游戏[8]、围棋[9-11]、德州扑克[12]、无人驾驶[13]等领域取得了突破进展, 部分场景中已经达到或超越了人类专家水平. 然而基于强化学习的智能体在更为复杂的场景中面临着感知状态空间巨大、奖励稀疏、长程决策动作组合空间爆炸等难题[14].
战争对抗作为一种复杂对抗场景, 一直是智能体策略生成研究的重点, 并越来越受到关注[15-17], 但当前研究还缺少实质性的进展, 特别是在人机对抗中[18], 人类对手策略变化造成的环境非静态性会使智能体显得呆板、缺少应变能力.
针对陆军战术级对抗场景中智能体状态动作空间复杂和行为模式固定的问题, 以中科院“庙算·智胜即时策略人机对抗平台”陆军战术对抗兵棋(以下简称“庙算”陆战对抗兵棋)为实验平台, 提出了基于博弈混合策略的智能体对抗策略生成方法. 本文工作主要有3 个方面:
1)对陆战对抗中实体动作进行抽象、分层, 建立智能体任务分层框架, 降低问题求解的复杂度.
2)对陆战对抗实体任务中关键要素进行分析,构建对抗问题博弈模型, 并给出收益矩阵的计算方法.
3)给出陆战对抗兵棋推演场景中智能体混合策略均衡的求解方法, 对本文所提方法的可行性进行了验证.
1 陆战对抗智能体框架设计
针对复杂人机对抗问题, 通常使用分层任务分解与任务协同机制对决策空间进行维度约减[18]. 本节使用任务分层的方法对陆战对抗问题进行形式化, 构建陆战对抗场景中基于任务分层的智能体行为模型.
1.1 智能体框架
在陆战对抗场景中, 智能体通常用于指挥红方或蓝方的所有兵力实体, 与人类指挥的另一方兵力实体进行对抗, 完成战斗消耗和目标夺控的任务. 图1 为“庙算”陆战对抗兵棋平台中一个战术级对抗想定, 其中战斗实体类型主要有步兵、坦克、战车、无人车、巡飞弹等.
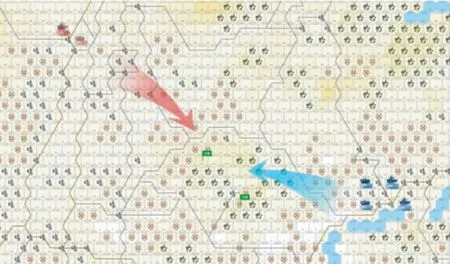
图1 陆战对抗兵棋战术级想定示意图Fig.1 Schematic diagram of a tactical-level war game scenario of land warfare confrontation
对抗过程中, 智能体需要根据环境的状态和己方实体之间的协同关系, 决策各个实体的机动、射击、掩蔽等原子动作, 由此构成智能体的基本策略框架如图2 所示. 本文重点研究单个任务执行策略生成方法, 多个实体之间的协同策略在2.3 节给出.
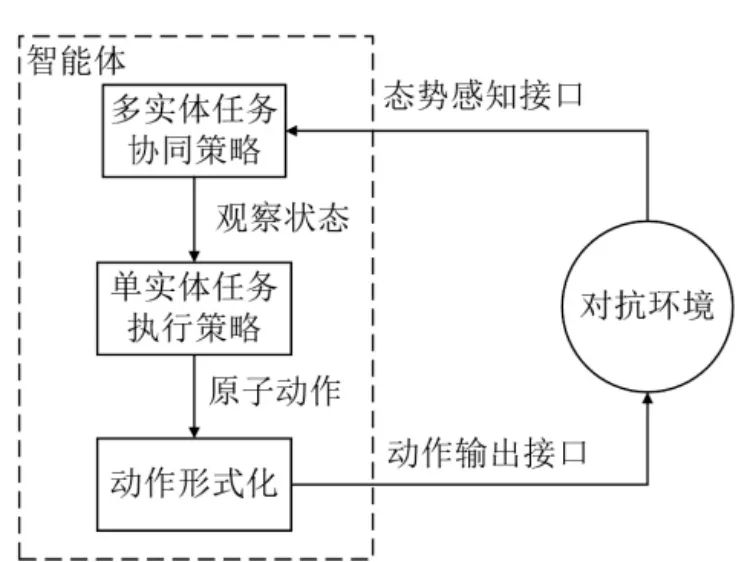
图2 陆战对抗场景中智能体框架Fig.2 The agent framework in land warfare confrontation scenario
马尔可夫决策过程(Markov decision process,MDP)给出了智能体决策的基本模型, 用四元组
在“庙算”陆战对抗兵棋中, 某一时刻的环境状态包含战斗实体类型、位置、班(车)数、机动状态、对抗区域的地形等信息, 对于对抗一方来说, 观察状态只包含己方实体能看到的信息. 实体可选动作集合包括机动、射击、引导射击、夺控、下车、掩蔽等动作. 状态转移概率由推演规则决定. 动作回报主要通过夺控得分和兵力损失情况进行量化.
陆战对抗中地形复杂性、实体类型和动作多样性、状态转移的高随机性、回报的稀疏性等造成了智能体决策问题的复杂性[19], 构建观察状态到原子动作的映射是十分琐碎和困难的. 人类在完成复杂任务时, 通常将其抽象分解为更加具体的子任务, 任务的完成由下一级子任务或动作组合实现, 分层任务网、分层强化学习等方法都使用了任务分层的思想[20-21]. 作战任务通常采用任务层次化方法建模[22], 在陆战对抗场景中, 可将复杂任务分解为若干子任务进行策略求解.
任务是为实现特定意图而从事的有目的的活动,可用三元组Mi=
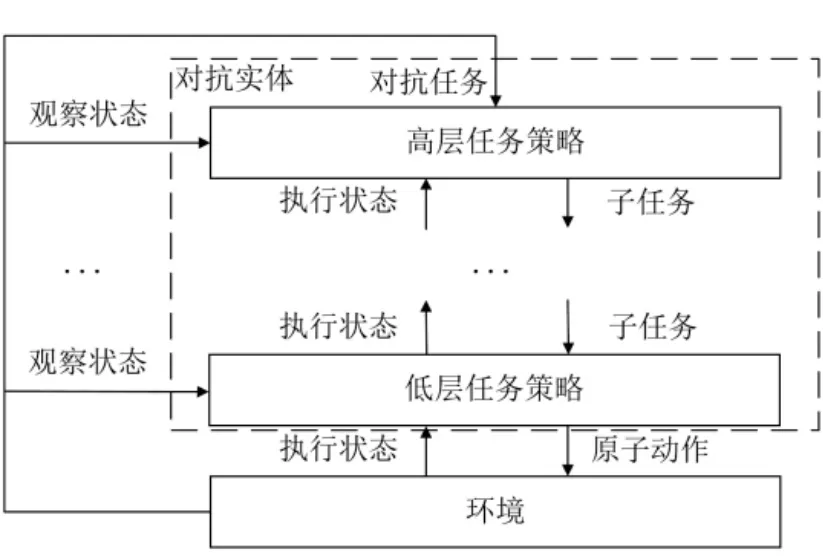
图3 基于任务分层的单个实体动作架构Fig.3 The single entity action architecture based on task hierarchy
1.2 单个实体行为建模
陆战对抗中单个实体任务是通过射击、引导射击、夺控等动作实现的, 而这些动作执行要受到其所在点位的通视情况、与目标距离和高差等条件约束,在实施这些动作之前战斗实体需要先机动到合适的点位, 而后才能通过实施相应动作达到收益最大化的目的. 由上, 陆战对抗中实体任务可定义为:实体以实施观察、射击、夺控等动作和阻止对手实施观察、射击、夺控等动作为目的, 而采取的从当前点位机动到满足动作实施条件的点位直到完成相应动作的活动.
根据陆战对抗中动作目的不同, 战斗实体任务可被抽象为侦察、攻击、躲避、夺控、兵力投送等任务, 可用1.1 节所述
陆战对抗中, 无人车用于协同坦克、战车等完成火力消耗和夺控任务, 主要任务是发现对手位置和引导射击. 用U 代表无人车, 无人车子总任务为MU,0,对应的终止状态集合TU,0={无人车被消灭, 达到最大推演时间tmax}. 任务目标完成度RU,0通过对手战损值和己方战损值差值衡量, 差值越大RU,0值越高. 如图4 所示, 本文将无人车子任务分为侦察、攻击、躲避、夺控4 种, 分别用MU,R、MU,S、MU,H、MU,C表示, 则无人车总任务MU,0所包含的动作集合可表示为AU,0={MU,R, MU,S, MU,H, MU,C}.
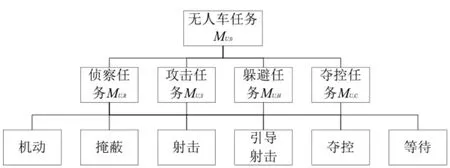
图4 无人车任务分层架构Fig.4 The task hierarchical architecture of unmanned vehicle
无人车侦察任务MU,R定义为无人车以观察到对手为目的, 而采取的从当前点位机动到满足观察条件的点位直到观察到对手的活动. 其对应的终止状态集合TU,R={没有符合完成侦察任务的点位;战车可用于引导射击的弹药消耗完毕;对手车辆全被消灭导致没有引导射击任务;己方夺控棋子被消灭导致无人车需要执行夺控任务}. AU,R={机动, 掩蔽, 引导射击,夺控, 等待}. 任务目标完成度RU,R通过观察到对手机动路径中点位数量进行衡量, 观察到的点位越多RU,R值越高.
无人车攻击任务MU,S定义为无人车以实施射击动作为目的, 而采取的从当前点位机动到射击收益最大的点位直到完成射击动作的活动. 其对应的终止状态集合TU,S={没有符合完成射击任务的点位;武器冷却时间大于对手射击到无人车的时间;己方夺控棋子被消灭导致无人车需要执行夺控任务}. AU,S={机动, 掩蔽, 射击, 引导射击, 夺控, 等待}. 任务目标完成度RU,S通过对手战损值和己方战损值差值衡量,差值越大RU,S值越高.
无人车躲避任务MU,H定义为无人车以不被对手射击为目的, 而采取的从当前点位机动到对手射击收益最小点位的活动. 其对应的终止状态集合TU,H={没有符合完成躲避任务的点位;武器冷却时间小于对手射击到无人车的时间;己方夺控棋子被消灭导致无人车需要执行夺控任务}. AU,H={机动, 掩蔽, 夺控,等待}. 任务目标完成度RU,H通过己方战损值衡量,己方战损值越小RU,H值越高.
无人车夺控任务MU,C定义为无人车以获得指定点位控制权为目的, 而采取的从当前点位机动到指定夺控点位并取得控制权的活动. 其对应的终止状态集合TU,C={没有符合到达夺控点的路径;夺控点或相邻单元格有对手棋子不能进行夺控}. AU,C={机动,掩蔽, 夺控, 等待}. 任务目标完成度RU,C通过己方夺控得分和战损值差值衡量, 差值越大RU,C值越高.
无人车任务执行算法如下.

1 初始化:高层任务MU,0、高层终止状态集合TU,0、高层任务策略πU, 0.子任务集合{MU, R, MU, S, MU, H, MU, C},各子任务对应的终止状态集合分别为TU, R、TU, S、TU, H、TU, C,执行策略

分别为πU,R、πU,S、πU,H、πU,C 2 根据高层任务策略πU,0 和初始状态o0 选择当前的子任务M=πU,0(o0)∈{MU,R, MU,S, MU,H, MU,C},子任务M 对应的终止状态集合记为T,子任务对应策略记为π 3 从时间步t=0 到最大时间tmax:4 如果当前观察状态ot∈TU,0,转到步骤8 5 如果当前观察状态ot∈T,转到步骤6,否则转到步骤7 6 根据观察状态ot 选择新的子任务M=πU,0(o0),更新对应的终止状态集合T 和策略π 7 根据观察状态ot 选择并输出原子动作at=π(ot)8 终止任务MU,0
其中, πU,0代表高层任务策略, πU,R、πU,S、πU,H、πU,C代表侦察、攻击、躲避、夺控4 种子任务的策略. 各个策略可通过贝叶斯网络(Bayesian networks)[23]、汤普森采样(Thompson sampling)[24]等方式进行环境建模和策略求解, 也可采用深度强化学习方式求解. 本文高层策略通过使用有限状态机进行控制, 重点研究子任务的策略生成方法, 主要通过构建策略式博弈模型求解混合策略, 将在第2 节中详述.
2 对抗任务博弈策略生成算法
通过分析, 任务Mi执行过程可以看作由三元组
2.1 策略式博弈模型和博弈解
陆战对抗问题是对抗双方之间的博弈问题. 策略式博弈(strategic-form game)是博弈问题中最基本的形式, 用三元组表示, 其中N={1, 2, …, n}表示所有参与者构成的有限集合;Ai表示参与者i∈N 的动作集合, 所有参与者的联合动作空间用表示, 其中一个联合动作向量用表示;表示参与者的收益(奖励)函数, Ri(a)表示在联合动作a 下参与者i的收益. 策略式博弈又称矩阵博弈, 可以用一个n 维张量表示动作和收益的关系, 多数博弈问题都可以转化成策略式博弈问题进行求解. 陆战对抗通常是红蓝双方对抗(n=2), 假设双方收益函数取相反值,即, 此时对抗问题建模为二人零和博弈问题.
在陆战对抗场景中, 状态通常是部分可观察的,同一观察状态可能对应着不同的对手状态, 此时选择某一动作通常只能在部分对手状态下取得正收益,不存在严格优势的纯策略. 在人机对抗中, 如果智能体采用纯策略, 人类对手经过重复对抗会掌握智能体策略, 并在后续对抗中采取反制策略. 因此, 在陆战对抗场景中, 当不存在严格优势的纯策略时, 智能体采用混合策略要严格优势于纯策略. 下面以陆战对抗兵棋推演中战斗实体子任务为例给出混合策略求解方法.
2.2 陆战对抗博弈模型和策略生成算法
在陆战对抗中, 用(x1, x2, …, xj)表示智能体子任务Mi执行过程中的位置序列, 引导射击、射击、夺控等动作通常发生在最后一个点位xj(以下称为目标点位), 因此, 任务完成效果Ri与最后一个点位xj的关联性较强, 与前j-1 个点位关联性较弱. 基于上述分析, 本文重点研究目标点位的决策方法, 对于从任务出发点x1到目标点xj之间的机动路径可使用Dijkstra、A*等算法得到[25], 不作重点研究. 智能体到达目标点位后的观察、射击、夺控等其他动作按照收益最大原则满足条件即可执行, 本文使用脚本规则控制.
在陆战对抗中, 任务Mi目标点位的选择主要受到两类条件约束:1)任务时效性, 即子任务是根据当前态势选择的, 通常只在一段时间内有效, 如果在有限时间内无法安全到达目标点位, 或者到达后态势改变导致任务无法执行, 此类点位不应作为目标点位;2)任务完成度, 即受到目标点位坐标、高程等因素影响, 到达目标点位后实施目标动作, 能否得到高的收益. 在兵棋推演场景中多数点位是不能满足时效性要求的, 是严格劣势策略. 因此, 可先根据时效性要求对敌我双方目标点位空间进行压缩, 得到敌我双方候选目标点位集合, 再通过建立收益矩阵进行混合策略求解. 下面以红方无人车侦察任务MU,R为例给出混合策略的求解方法, 其他任务混合策略求解方法可参考此方法.
无人车侦察任务MU,R通常在对抗开始阶段执行,目的是在对手夺控或威胁到红方战车等实体前, 完成观察和引导射击任务, 同时避免被对手攻击, 相关要素如图5 所示. 其中六角格不同的背景颜色表示点位高程不同, 白色背景点位高程最低. 绿色小旗所在点位为夺控目标. 红色正方形点位代表红方战车选取的兵力投送点位, 横线阴影区域代表能通视战车的区域. 蓝色三角形代表蓝方坦克出发点位, 蓝色实线代表其中一条可选的攻击红方战车路径, 蓝色虚线代表一条可选的夺控路径. 红色菱形代表一个无人车侦察任务候选目标点位, 绿色虚线代表其对对手坦克机动路径上某一条点位的观察通路. 红方无人车执行侦察任务时, 需要根据战车兵力投送点位和夺控点周围地形, 选择合适的点位实现对蓝方坦克的通视, 同时避免被对手攻击.
用函数see(x1, x2)表示点位x1对x2的通视情况,能通视则see(x1, x2)=1, 否则see(x1, x2)=0, xchariot表红方战车的停车点,对战车构成威胁的点位集合为Xchariot={x|see(x, xchariot)=1}, 对应图5 中横线阴影区域. 用E表示对手棋子集合, xe表示对手棋子e 当前点位, xt表示无人车当前点位, xmain表示主要夺控点, time(x1, x2)表示从x1机动到x2需要的时间, timestop表示无人车从机动状态转到可引导射击状态的时间. 则红方无人车侦察任务目标点位xtarget的候选集合为
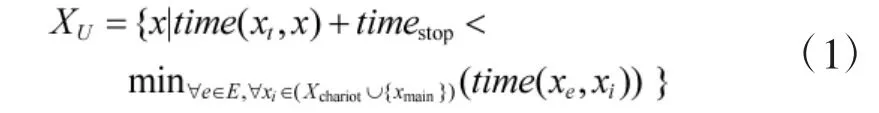
其含义为无人车要在对手夺控和能够攻击到红方战车之前到达侦察点位, 设无人车侦察任务候选点位集合为.
根据对手意图, 对手动作集合YE为对手夺控目标点位集合YE,C和进攻目标点位集合YE,S的并集.由于侦察效果是通过对手机动路径上点位的通视情况体现的, 这里使用对手到达目标点位的机动路径代替对应的目标点位进行收益计算, 用route(x1, x2)表示从点位x1机动到x2路径包含的点位序列. XE,Hist表示红方最后一次观察到的对手所有棋子点位集合.Xcities表示所有的夺控点位集合. 则对手夺控动作集合为
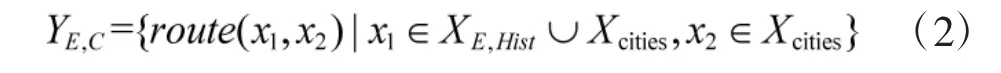
进攻动作集合为
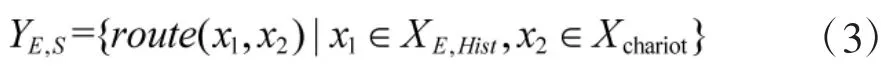
对YE,C、YE,S求并集, 得到对手棋子动作集合,表示为.
对于无人车侦察任务MU,R, 其完成效果RU,R是通过是否观察到对手评价的. 假设无人车出现在点xU,i, 对手出现在点xE,j, 无人车收益计算方式为:
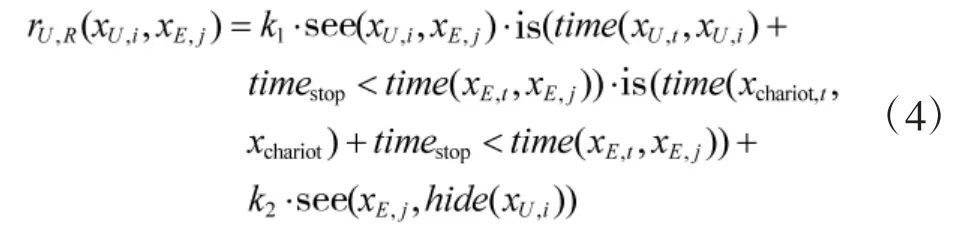
其中, is(·)为条件判断函数, 满足取1, 否则取0;xU,i表示无人车当前点位;xchariot,i表示战车当前点位;xE,t表示对手棋子当前点位;hide(xU,i)表示无人车在xU,i处保持掩蔽状态. 式(4)的含义为无人车收益为引导射击收益和被攻击收益之和:如果能够在对手到达点位xE,j之前完成对xE,j的观察和引导射击准备, 则引导射击收益为正值(设单次收益值为k1), 否则引导射击收益为0;如果被对手看到且被对手射击, 则收益为负值(设单次收益值为k2). 构建收益矩阵时, 红方动作为点位xU,i、对手动作为路径yE,j时, 无人车收益为:
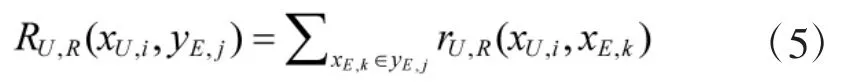
通过上述计算方式得到无人车侦察任务收益矩阵如下.
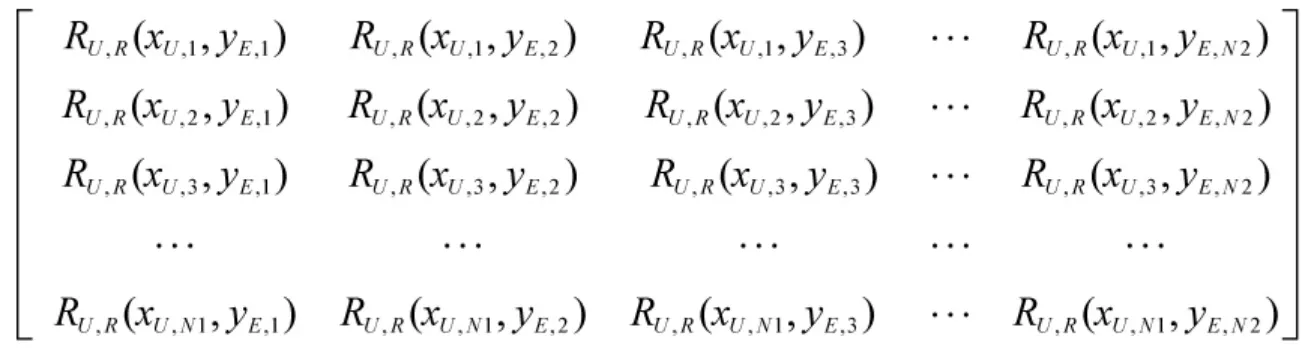
该矩阵对应的的最优解称为混合策略均衡, 可先剔除严格劣势策略(对应的选择概率为0), 而后使用线性规划方法求解[26]. 用p(xU,i)表示点位xU,i的选择概率, 对应的线性规划问题为
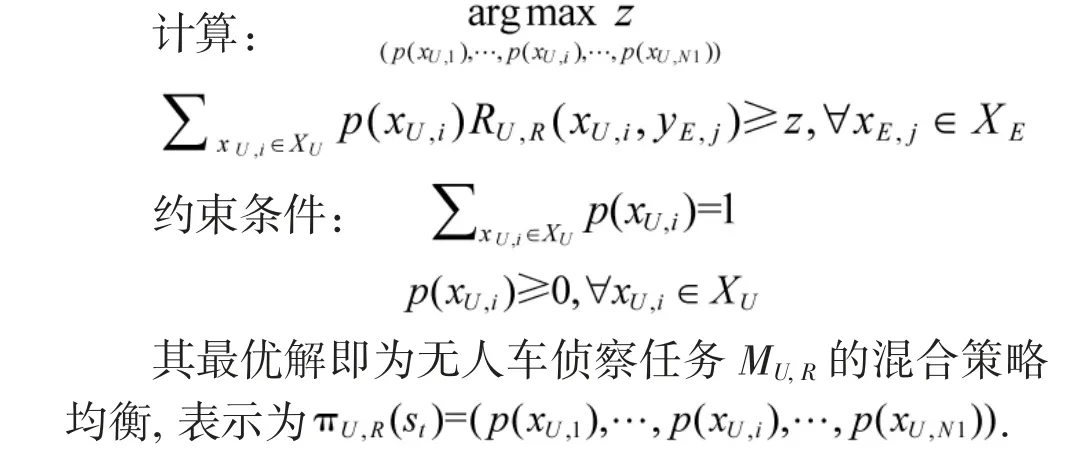
以上是无人车侦察任务的混合策略求解方法,其他任务求解方法类似. 夺控任务不需要选择目标点, 只是单纯的路径规划问题, 本文不进行研究, 只给出躲避任务和射击任务收益函数构建方法.
无人车躲避任务只考虑对手对我方的通视, 不考虑我方对对手的通视, 收益函数表示为:
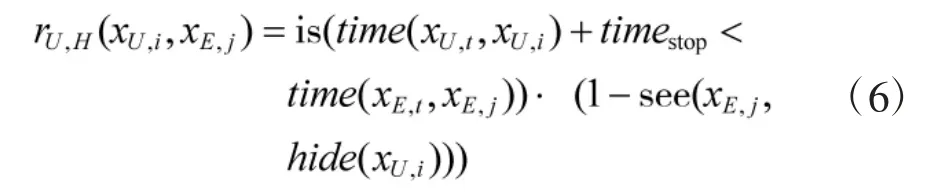
无人车射击任务收益通过攻击等级进行评价,用式(7)表示,其含义为:当双方互相通视时,先进入射击状态一方收益为正;当单方通视时,通视一方收益为正;当互不通视时, 收益为0. 其中, level(x1, x2)表示点位x1处棋子对x2处棋子射击的攻击等级,timeshoot(x1,x2)表示棋子从点位x1处机动到x2处并进入准备射击状态的时间.
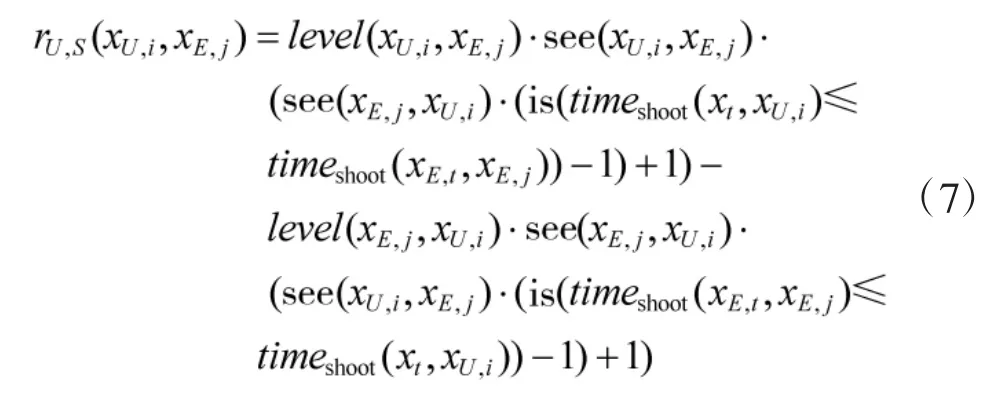
2.3 多实体任务策略协同
假设陆战对抗中己方有Z 个战斗实体, 实体集合用Entity={entity1, entity2, …, entityz}表示. 当同一时刻有多个实体需要决策时, 如果直接求解联合策略,其动作空间是十分巨大的, 同时也不利于不同场景策略的迁移. 而采用分布式决策时实体之间通常会因为追求各自收益最大化而产生竞争关系. 针对上述问题, 可将多实体任务并行决策问题转化为顺序决策问题, 将实体任务划分为不同的层级(优先级), 先决策层级高的实体任务, 后决策层级低的实体任务.
不同实体任务之间层级高低通过风险度D 评价,其计算方法为, 其中分别表示实体entityi执行当前子任务Mi,t可能得到的最大收益和最小收益. D 越大对于整体收益的影响越大, 在所有实体中主导性越强, 在顺序决策中的层级越高, 反之D 越小层级越低. 假设Entity 中实体之间的风险度满足,则实体决策顺序如图6 所示.
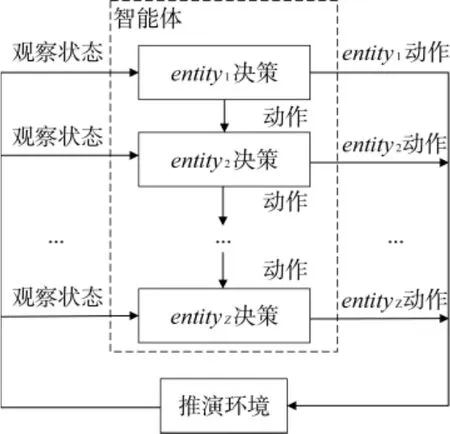
图6 多实体顺序决策流程Fig.6 The multi entity sequential decision-making process
在陆战对抗兵棋推演中, 令Rmax(Mi,t)=夺控分+对手战损分,Rmin(Mi,t)=-己方战损分.由于战车战损会影响到步兵、无人车和巡飞弹, 任务风险度最大. 无人车没有装甲, 在与对手交火时战损值最大, 风险度次之. 坦克具有机动灵活的射击能力和较强的装甲防护, 任务风险度小于无人车. 步兵在交火过程中受到射击时通常损失较小. 巡飞弹不会受到攻击. 因此,本文按照战车、无人车、坦克、步兵、巡飞弹的顺序进行决策.
3 实验与分析
本文以“庙算”陆战对抗兵棋中分队级对抗想定为场景进行仿真实验, 其中红方战斗实体包括步兵、坦克、战车、无人车、巡飞弹等类型, 蓝方战斗实体包括步兵、坦克、战车等类型, 夺控目标通常包含主要夺控目标和次要夺控目标.
3.1 智能体实现
智能体采用集中控制的方式控制各个棋子, 观察状态为己方所有棋子观察状态的并集(不考虑通信问题). 每个时间步, 智能体按照战车、无人车、坦克、步兵、巡飞弹的顺序依次决策己方棋子动作. 其中步兵和巡飞弹由于其任务风险度小、规律性强, 直接使用脚本规则控制. 步兵主要执行夺控和守控任务, 按照最近夺控点、主要夺控点、守控的顺序动作.巡飞弹主要执行侦察任务, 根据对手棋子机动速度和射击准备所需的时间, 采取不同的侦察频率, 机动速度越快、射击准备所需时间越短侦察频率越高, 坦克最高、战车次之、步兵最低. 战车、无人车、坦克使用第1 节所述分层动作架构, 高层任务使用有限状态机控制子任务切换, 子任务使用博弈模型进行目标点位决策, 基于混合策略的智能体决策流程如图7 所示.
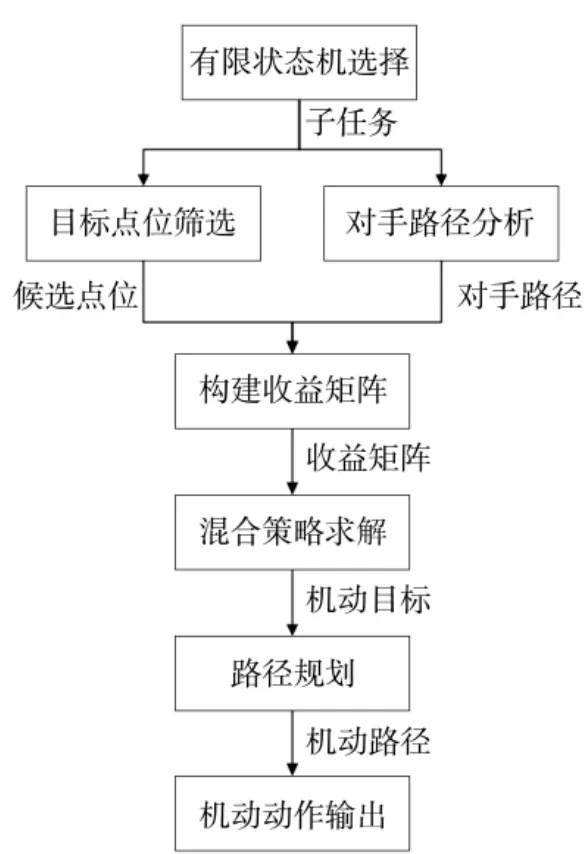
图7 基于混合策略的智能体决策流程Fig.7 The agent decision-making process based on hybrid strategies
为了提高计算效率, 在构建收益矩阵前, 根据规则对双方候选点位进行筛选. 由于观察距离最大为25, 射击距离最大为20, 将棋子侦察任务候选区域限制在主要夺控点距离25 范围之内, 将棋子攻击任务候选区域限制在主要夺控点距离20 范围之内. 因此,计算式(1)中威胁区域时, 实际候选点位集合是满足战车射击范围、夺控点射击范围和最短路径要求的点位, 满足式(8).
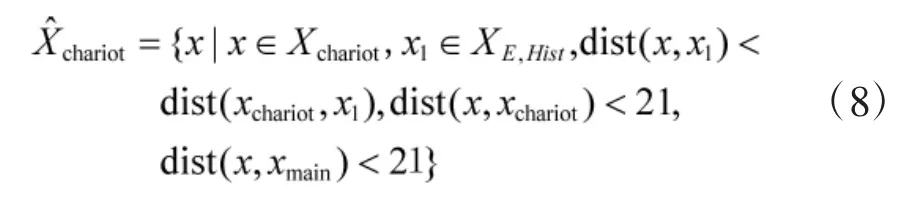
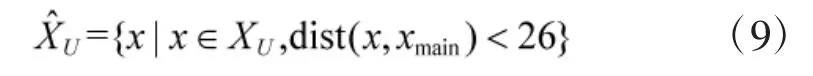
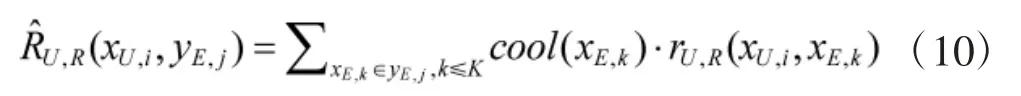
得到收益矩阵后, 矩阵中存在己方收益或对手收益全为负值的点位, 这些点位是严格劣势策略, 应当去除. 本文通过求解帕累托前沿的方法反复剔除己方和对手的严格劣势策略, 进一步压缩收益矩阵,算法流程如算法2 所示.

算法2:基于帕累托前沿的目标候选集合压缩算法1 初始化:己方候选动作集合images/BZ_87_1797_1943_2165_1988.png, 对手选动作集合images/BZ_87_1555_2004_1906_2048.png, 己方收益计算函数images/BZ_87_1341_2064_1407_2117.png,Xtarget={XU,1}2 从i=2 到N1:3 遍历所有x*∈Xtarget:4 如果images/BZ_87_1485_2239_2101_2294.png, 将x* 从Xtarget 中剔除5 如果images/BZ_87_1472_2363_2092_2421.png,跳转到步骤2 6 将xU,i 加入到Xtarget 中
在使用上述算法对于目标点位候选集合进行压缩过程中, 以下两种特殊情况需单独处理:
1)己方多个候选动作收益相同时, 其选择概率相同. 在计算过程中, 只保第1 个动作对应的行, 最终求得的选择概率为与其收益相同的所有可选动作的概率之和. 对于对手收益相同的动作, 对己方最终策略生成没有影响, 只保留一个即可.
2)如果对手有严格优势策略, 并且其对应的己方所有动作收益值相等时, 己方在这些动作中进行等概率选择的意义并不大. 针对上述情况, 考虑到实际对抗中对手不总是完全理性的, 此时选择剔除对手的严格优势策略, 即选择在对手不是完全理性的情况下求解最优策略.
通过使用上述方法对己方和对手可选动作集合进行压缩后, 使用Python 调用线性规划函数scipy.optimize.linprog 求解各目标点位选择概率. 而后根据动作概率选择目标点位, 并根据目标点产生机动路径和其他动作.
本文实验中路径规划直接使用A*算法搜索代价最小的路径. 其中从任意坐标x1机动到相邻坐标x2的代价cost(x1, x2)计算方式为:
cost(x1, x2)=time(x1,x2)+α·seen_num(x2) (11)其中,time(x1,x2)指从x1机动x2的时间, seen_num(x2)指可能观察到x2点位的对手棋子数量, 系数α 取远大于time(x1, x2)的常数.
3.2 实验结果与分析
使用“庙算”陆战对抗兵棋中水网稻田地(201043 1153)和高原通道(2010211129)作战想定, 通过机机对抗和人机对抗两种方式对智能体策略进行测试.机机对抗使用“庙算”陆战对抗平台开源的DEMO、WargameAILib_1.0 中的级别2 的智能体(不使用兵力聚合、解聚动作)进行测试.
图8 为水网稻田地想定中红方棋子部署后的观察视图, 由于各个棋子采用博弈策略进行部署, 其点位较为合理, 能够对对手攻击路径和夺控路径形成较好的火力封锁效果.
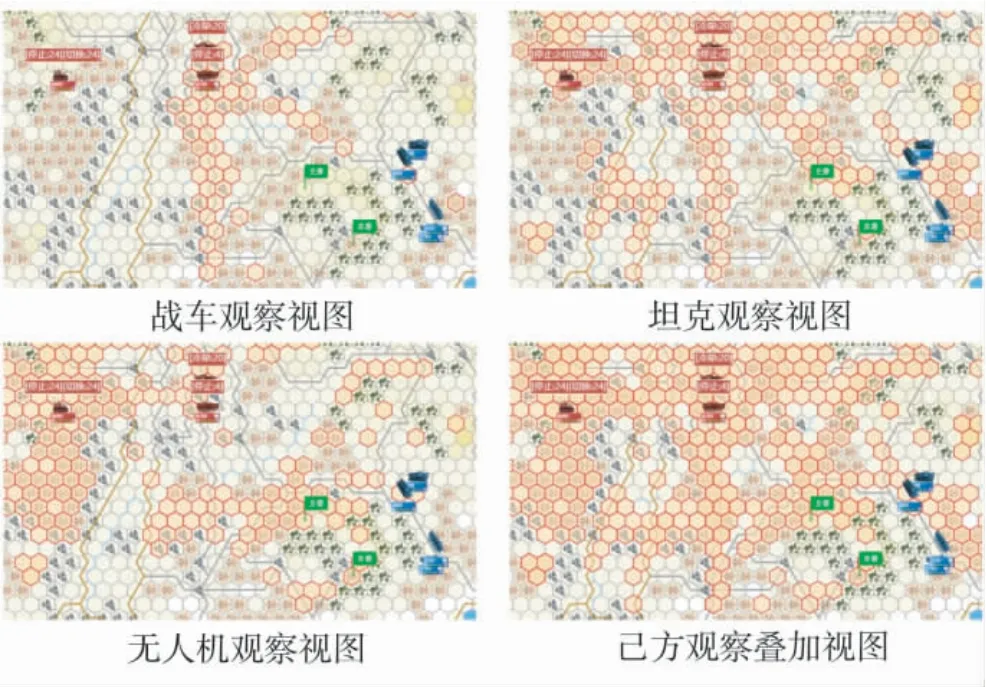
图8 红方棋子采用博弈策略部署后观察视图Fig.8 The observation views of red chess pieces after deployment with game strategies
智能体与不同对手对抗胜率统计如表1 所示,净胜分分布如图9 所示. 两种不同想定测试结果证明该方法得到的智能体能直接适用不同的对抗想定,而不需要人类专家知识根据想定预先指定智能体任务目标点位.
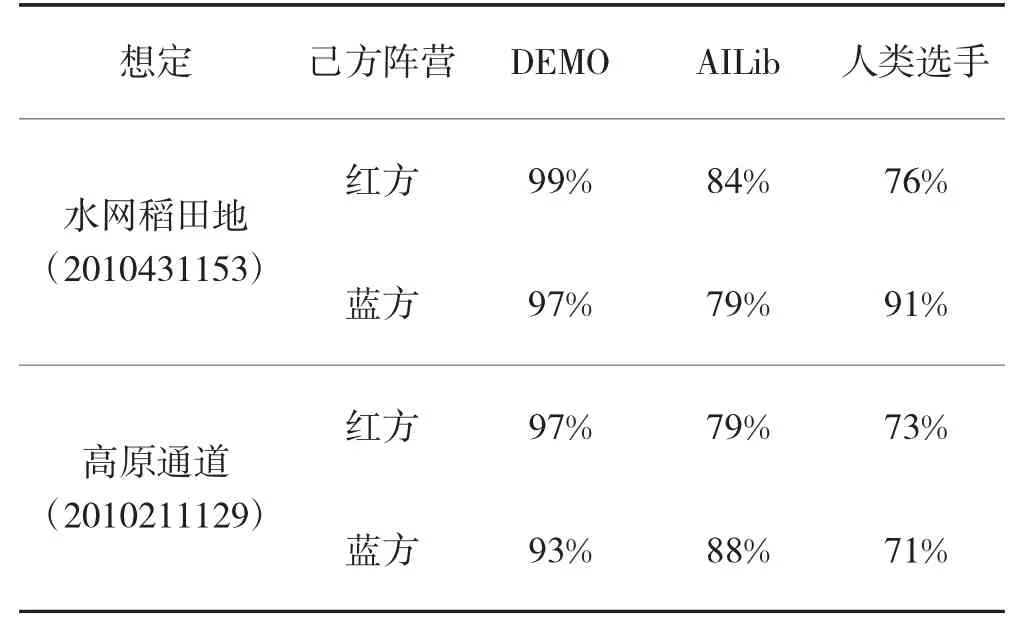
表1 智能体测试胜率统计Table 1 The statistics of winning rate of agent test
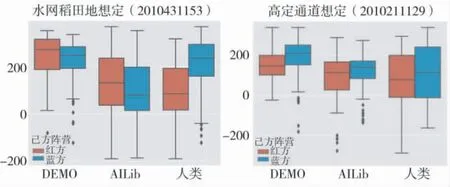
图9 对抗成绩分布Fig.9 The box-plot of confrontation results
在与开源的AI 库中的智能体进行对抗过程中,由于本文智能体的策略是通过博弈矩阵求解得到的,具有较强的可解释性, 胜率较高. 另一方面对于当前AI 库中智能体的策略来说, 本文所提出的智能体的混合策略中的部分候选动作是优势策略, 部分是劣势策略, 同时需要考虑到兵棋推演系统裁决规则的高随机性, 对抗成绩存在负成绩.
由于本文所提出的智能体使用混合策略进行目标点位选择的, 相同态势下智能体可能会采取不同的目标点位, 因此, 在与人类重复对抗中, 能够有效避免因为使用纯策略导致行为模式固定的问题, 不容易被人类对手发现动作规律和找到反制策略, 具有较高的胜率.
综上, 实验证明本文提出的陆战对抗智能体博弈策略具有较强的可解释性和灵活性, 与现有开源AI 和人类进行对抗都具有较高的胜率. 混合策略的运用使智能体行为模式更加多样, 能够有效避免因为行为模式固定被人类对手针对的问题.
4 结论
针对陆战对抗中智能体策略求解困难和行为模式固定的问题, 以陆军战术对抗兵棋推演为场景, 给出博弈矩阵构建和混合策略求解的方法, 并通过离线机机测试和在线人机测试对智能体性能进行了测试. 实验证明该方法得到的智能体策略能够适用于不同的对抗想定, 同时能够有效克服智能体行为模式固定的问题. 该方法得到的智能体策略, 可以直接作为复杂对抗场景中智能体子任务执行方法, 也可用于为基于强化学习、遗传算法等算法的学习型智能体初始策略学习提供样本, 有效解决复杂对抗场景中神经网络模型冷启动的问题. 由于该方法得到的智能体策略是通过问题抽象简化得到的, 其收益矩阵是针对子任务执行得到的近似最优解, 在收益矩阵构建和计算过程难免会存在要素遗漏, 在下一步工作中, 可与贝叶斯网、遗传算法、强化学习等相结合, 对智能体对抗策略进行进一步优化.
