天地一体化网络分散式算力路由控制策略

李洪钧 任保全 巩向武 国晓博 任智源

1.军事科学院系统工程研究院系统总体研究所 北京 100101 2.军事科学院系统工程研究院网络信息研究所 北京 100141 3.中国电子科技集团公司第五十四研究所 河北 石家庄 050081 4.西安电子科技大学综合业务网理论及关键技术国家重点实验室 陕西 西安 710071

天地一体化网络（space-ground integration networks, SGIN）能够为用户提供全球覆盖范围、快速建立联接、强大机动性能、信息实时处理等能力[1], 在全球侦察情报、全域联合指挥控制、天基信息支援、天地一体化智能协同抗干扰等各类军事应用中已成为研究热点[2-4]. 随着星间链路和星载计算处理技术的发展,大量数据传输、实时处理业务纷纷出现,对SGIN端到端传输能力、星上处理能力提出更高要求[5-8], 而路由控制将成为天地一体化网络高效联接和传输信息的核心基础.

针对上述挑战, 算力路由（computing-dependent route, CDR）作为算力网络中的关键技术被提出, 是一种将网络中的算力与传输结合起来的一种路由范式[9], 这种特质使得算力路由可以满足大量遥感图像传输和处理等等业务的需求. 但是, 现阶段的算力路由主要针对地面网络[10].同时, 为了屏蔽信息同步所带来的损耗, 算力路由仅适用于静态的网络中, 无法适应SGIN 的高动态环境. 因此, 本文重点研究SGIN 场景下的算力路由方法.

但是, 在SGIN 中实现算力路由会面临诸多问题.一般情况下, 路由和计算策略应该由计算能力强大的控制中心进行控制. 然而, 由于SGIN 网络节点的分步范围广、数量大, 很难找到一个控制中心对全网信息进行统一管理. 因此, 网络的无中心特点给分散式算例路由（dispersed computing-dependent route,DCDR）控制策略的制定带来很大的挑战. 许多学者在无中心动态网络的分散式算法方面有了初步的研究, 如S. Jošilo 系统平均参数作为分散式计算和路由策略制定的依据,但这种方法不适用于动态网络[11]. 为了适应网络动态性特点, 一些基于广播的算法被提出[12-13]. 但这些方法均忽略广播带来的时延损耗, 不适用于天地一体化网络这种远距离传输的场景.

因此, 本文提出一种面向SGIN 的DCDR 控制策略. 通过将任务的处理步骤建模为有向无环图（directed acyclic graph, DAG）模型, 构建一个由DAG 向SGIN 中单条路径映射的映射问题. 设计了一个改进的定向扩散算法（improved directional diffusion algorithm, IDDA）, 并将广播所产生的时延考虑在内. 在此算法的支持下, 实现了任务边传输、边计算、边制定映射策略的目标, 并将分散式算法的抗毁性优点发挥出来.

1 相关工作

随着云计算、雾计算和边缘计算[14-16]的发展, 分布式计算已经成为当前算网融合的发展主流. 文献[17]将边缘计算扩展到天空地海一体化网络（spaceair-ground-aqua integrated network, SAGAIN）, 将卫星视为移动边缘计算节点, 提供必要的计算和缓存功能. 算力网络作为一种算网融合的新技术方案, 能够通过网络算力间深度的连接, 将网络中无处不在的计算资源进行灵活调度[9], 而算力路由是实现端到端算力优化调度的核心技术点. 为了实现SGIN 网络中传输和计算结合, 本文重点研究在SGIN 场景下的算力路由方法. 但是, 如何在SGIN 中通过建模和算法实现算力路由仍面临诸多技术问题.

在早期阶段, 研究人员将不同的任务表示为不同的有向无环图, 为了优化网络业务的传输速率, 文献[18-19]研究了映射到网络拓扑上的不同任务DAG模型的最大传输速率, 但上述研究没有考虑任务的计算. 为了共同优化任务的计算和传输, 文献[20]提出了一种业务图边缘和节点映射技术, 该技术考虑了节点的计算能力约束, 但其不适用于复杂的任务DAG 模型. 针对这一问题, 文献[21]制定了复杂DAG的映射优化方案, 将任务DAG 的适用范围扩展到任何有向无环图模型. 然而, 上述研究都是基于有中心管理节点的网络, 在没有控制中心的情况下, 如何利用SGIN 中节点的计算能力在任务传输时处理任务仍是一个挑战.

2 系统模型

本节介绍了由卫星站和地面节点组成的SGIN架构, 并详细解释了DCDR 的定义. 基于SGIN 架构,建立了卫星节点与地面节点、星间链路和星地链路的运动模型,并对采用时空扩展图模型进行稳态化处理.

2.1 SGIN 架构

在对SGIN 进行建模之前, 首先介绍SGIN 的架构. 如图1 所示, 本文提出的SGIN 体系架构包括中轨道（medium earth orbit, MEO）卫星、低轨道（low earth orbit, LEO）卫星和地面节点. 其中, 采用带服务器的MEO 和LEO 卫星既作为算法执行节点, 协同制定DCDR 控制策略, 又作为主要计算和传输节点, 根据任务映射策略参与任务计算；地面节点作为传输节点与卫星节点共同为用户提供传输功能.

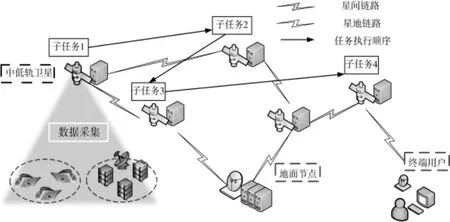
图1 SGIN 系统架构示意图Fig.1 Schematic diagram of SGIN system architecture

DCDR 的定义是SGIN 网络中基于计算的路由,因此, 路径的形成与用户任务的特点密切相关. 以图1 为例, 如果访问节点和目标节点已知, 则分别计算子任务1 和子任务4. 将其他不同的子任务映射到传输路径上的不同卫星节点, 从而实现任务边传输边计算. 此外, 应该注意到不同的卫星节点可以通过星间链路（inter-satellite links, ISLs）或星地链路联接.例如, 计算任务1 和任务2 的卫星是通过ISLs 连接的. 但是, 由于计算任务3 和任务4 的卫星之间的连接较差, 因此, 需要同时考虑ISLs 和星地链路.

2.2 动态SGIN 模型

根据卫星轨迹的可预测性, 卫星在任意时间的位置都可以被预测. 同样, 地面节点坐标可以根据地球的半径及自转速度计算得到. 因此, 本文将根据卫星和地面节点的相对位置, 对星间链路和星地链路进行建模, 构建动态SGIN 模型.

如图2 所示, 以地心为原点建立三维坐标系. 任何卫星节点的坐标都可以用开普勒六大参数来确定,其中,ai为半长轴,ei为偏心率,δi为倾角, Ωi为升交点赤经, ωi为近近地点幅角, fi（t）为真近地点角. 对于SGIN 中卫星节点的位置都可以通过三维坐标获得, 其中, M 为卫星个数. 文献[22]已经对星间链路建模进行了详细的阐述, 不做过多介绍. 基于文献[14]中的工作, 本文对星地链路建模进行详细的介绍.

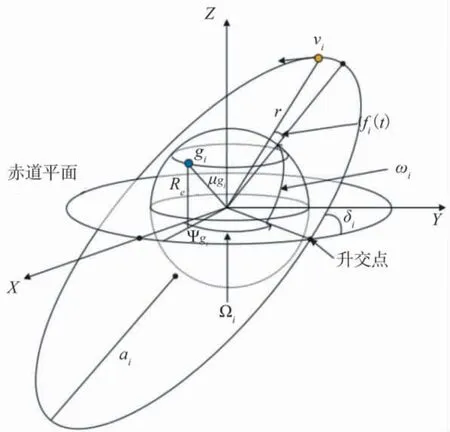
图2 地心坐标图Fig.2 Geocentric coordinate orientation

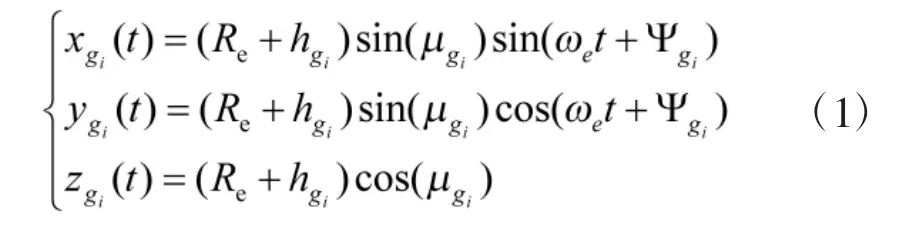
其中, Re是地球半径；ωe是地球自转角速度；分别可以通过经度和纬度得知.

地面节点位于地球表面. 卫星与地面节点之间的能见度取决于地面节点相对于卫星的仰角. 对于地面节点, 根据卫星坐标和地面节点坐标,可以计算得到其距离图3 中δ3可以通过三角关系计算得到.

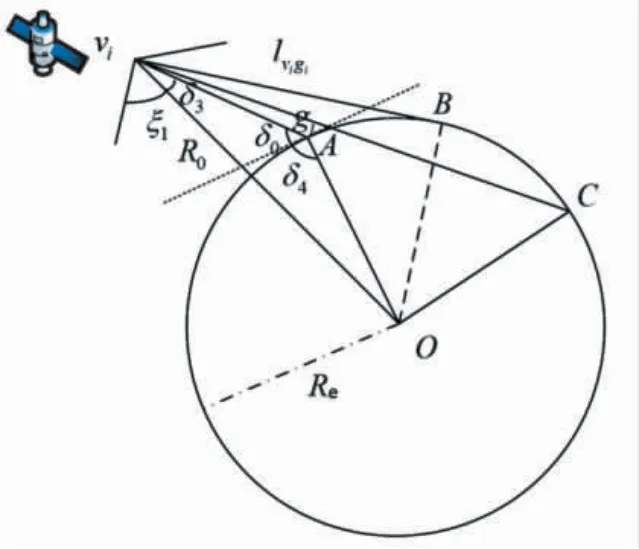
图3 卫星与地面节点之间的几何关系Fig.3 The geometric relationships between satellite and ground station

假设地面节点和卫星节点间的仰角为δ0, 则卫星vi和地面节点gi是否连通取决于δ0. δ3为地面节点和卫星节点之间的连线与卫星节点和地心之间连线的夹角. δ4为地面节点和卫星节点之间的连线与地面节点和地心之间连线的夹角.

如果δ4-90°<δ0, 则卫星节点和地面节点间物理可视, 即需要满足以下条件：

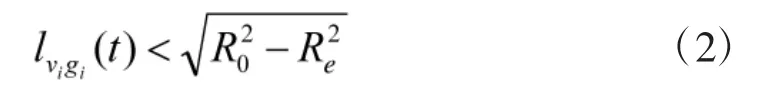
只有地面节点gi在卫星节点vi的覆盖范围之内,才可建立通信链路, δ3应满足以下条件：

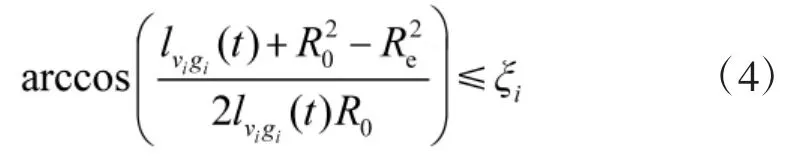
由于接收放大器可以恢复自由空间的传播损耗,本节不再过多关注自由空间损耗[23], 主要关注了另外两个衰减源：电离层闪烁和地面多径衰落. 在传输过程中, 信号通过不同的路径到达接收端. 接收信号是直视信号和通过建筑物、山脉、森林等其他信号的叠加. 为了同时分析电离层闪烁和多径衰落的影响,本文采用经典的双射线传播模型[15]. 反射系数Γ 由文献[24]给出.

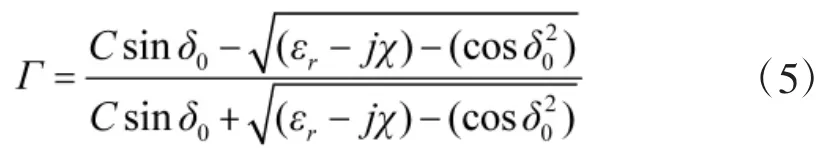
其中, ε0=8.854×10-12F/m, 并且σ 为多普勒频移. 根据文献[15]中σ=1, 两条反射路径的相位差为：

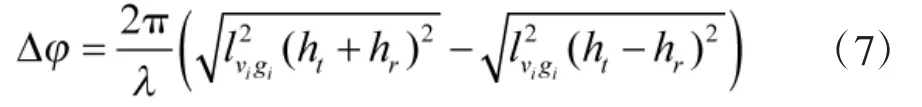
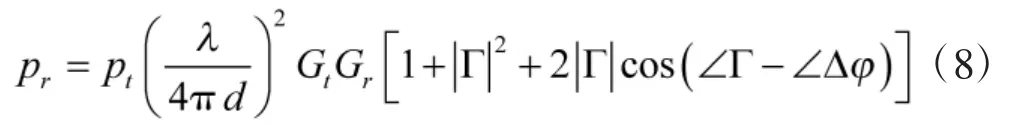
其中, pt是发射功率Gt和Gr分别是发射和接受天线增益. 然后, 根据香农公式, 星间链路上下行链路容量可以表示为：

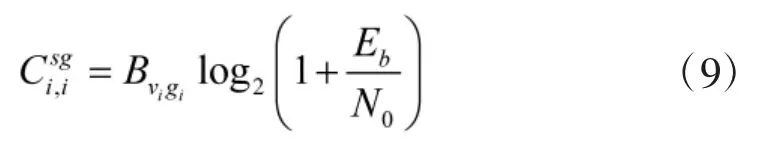
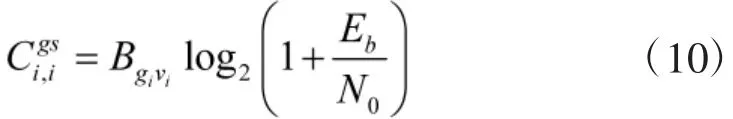
其中,

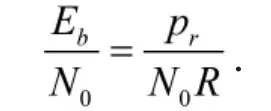
2.3 加权时空扩展图

由于SGIN 网络具有高动态性, 因此, 很难直接在动态网络中研究DCDR 控制策略. 为了解决SGIN拓扑频繁变化引起的路由不稳定问题, 本文采用SGIN 时空扩展图（SGIN time-expanded graph, SGINTEG）方法对SGIN 的动态拓扑进行稳态化处理[25-27].

文献[27]对卫星网络视同扩散图进行了的建模,本节在文献[27]的卫星时空扩展图的基础上考虑了星地链路, 构建SGIN 时空扩展图模型.

2.3.1 时空邻接矩阵

令时隙S 内的网络拓扑为01 邻接矩阵LS, 则矩阵中元素可以表示为：

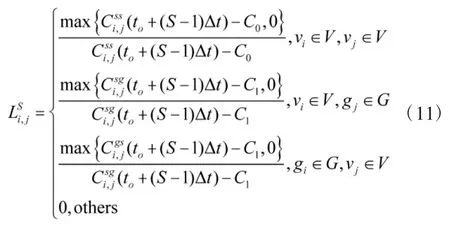
其中, C0和C1分别为星间链路和星地链路连通的容量门限的门限. 基于上述矩阵LS, 构建了SGINTEG的01 邻接矩阵.

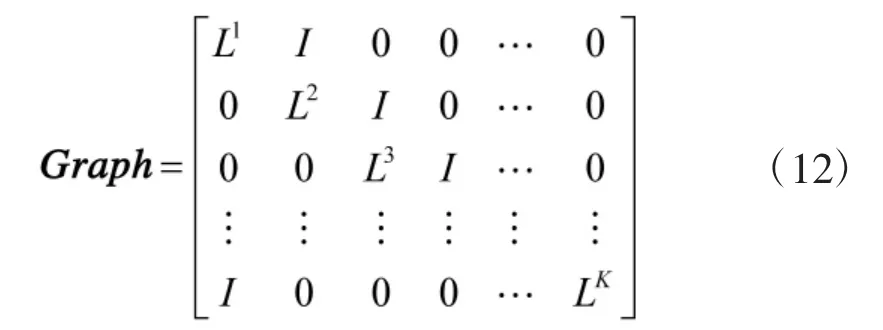
其中, I 是一个（M+N）×（M+N）的单位矩阵, 代表了时隙间的虚拟链路. 0 是一个（M+N）×（M+N）的0 矩阵代表, 非相邻的时隙没有虚拟链路直连. Graph 左下角的单位矩阵表示经过K 个时隙后, 网络拓扑回到初始状态.

2.3.2 时延加权邻接矩阵

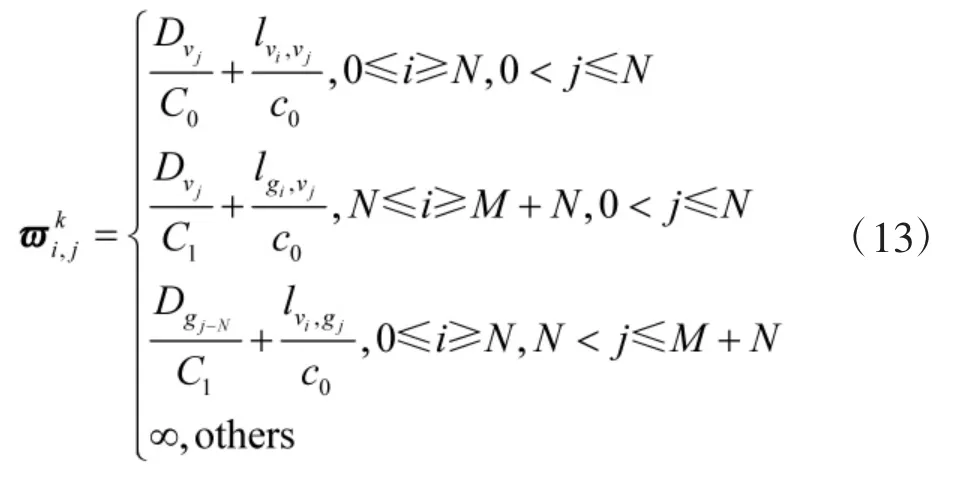
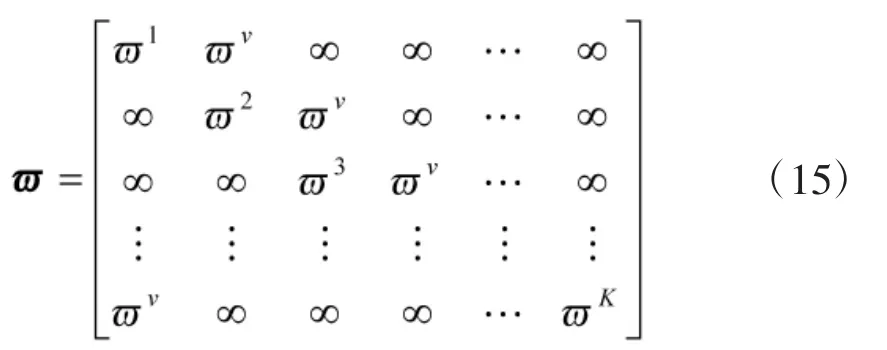
最后, 加权SGINTEG 可以表示为：

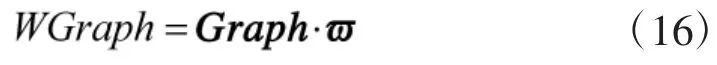
3 改进的定向扩散算法

SGIN 除了具有高动态的特点, 同时具有无中心的特点. 定向扩散算法作为一种分散式路由策略, 能够很好地适应大规模分散式网络[28]. 然而, 传统的定向扩散算法是一种无中心路由算法, 无法实现计算的映射. 这里提出一种改进的定向扩散算法, 源节点根据目标节点和不同的应用需求定义不同的任务类型,通过向网络广播兴趣消息来选择计算节点和建立路由. 中间节点通过接受计算和转发, 形成从源节点到目的节点的梯度. 自动生成任务节点映射和从源节点到目标节点的一条最优路径. 最后, 任务通过此路径和SGIN 中的节点完成计算和传输.

3.1 兴趣扩散

其中, s 为信息传播的跳数, 通常s=1, 如果一跳之内没有合适的节点映射, 则s>1.

除目标节点和源节点外, 其他子任务在传输时尽可能多地计算, 每映射一个子任务, 从前一个子任务映射的邻居节点中选择下一个子任务.

3.2 梯度建立

3.3 路径选择

在邻居节点的梯度已知后, 父节点根据梯度从小到大进行排序, 并根据这个顺序设置优先级, 梯度越小, 优先级越高.

4 仿真分析

为验证提出方案的有效性, 进行了大量的实验.通过分析不同DAG 下和不同任务终点情况下的DCDR 性能以及抗毁性, 根据仿真结果展示了不同DAG 的映射结果和不同任务量的映射结果, 卫星链路参数根据文献[32-33]设置.

基于星链星座选择了20 颗卫星和10 个地面节点构建一个SGIN. 卫星v1是源节点, v8是目标节点.根据地面节点观测更新时间, 每个时隙长度为60 s,第1 个时隙开始时间为上午8 点, 卫星轨道数据来自SpaceX 网站, 卫星计算能力为5 MHz～10 MHz 均匀分布. 星链星座中所选卫星编号、地面节点分别如表1、表2 所示.

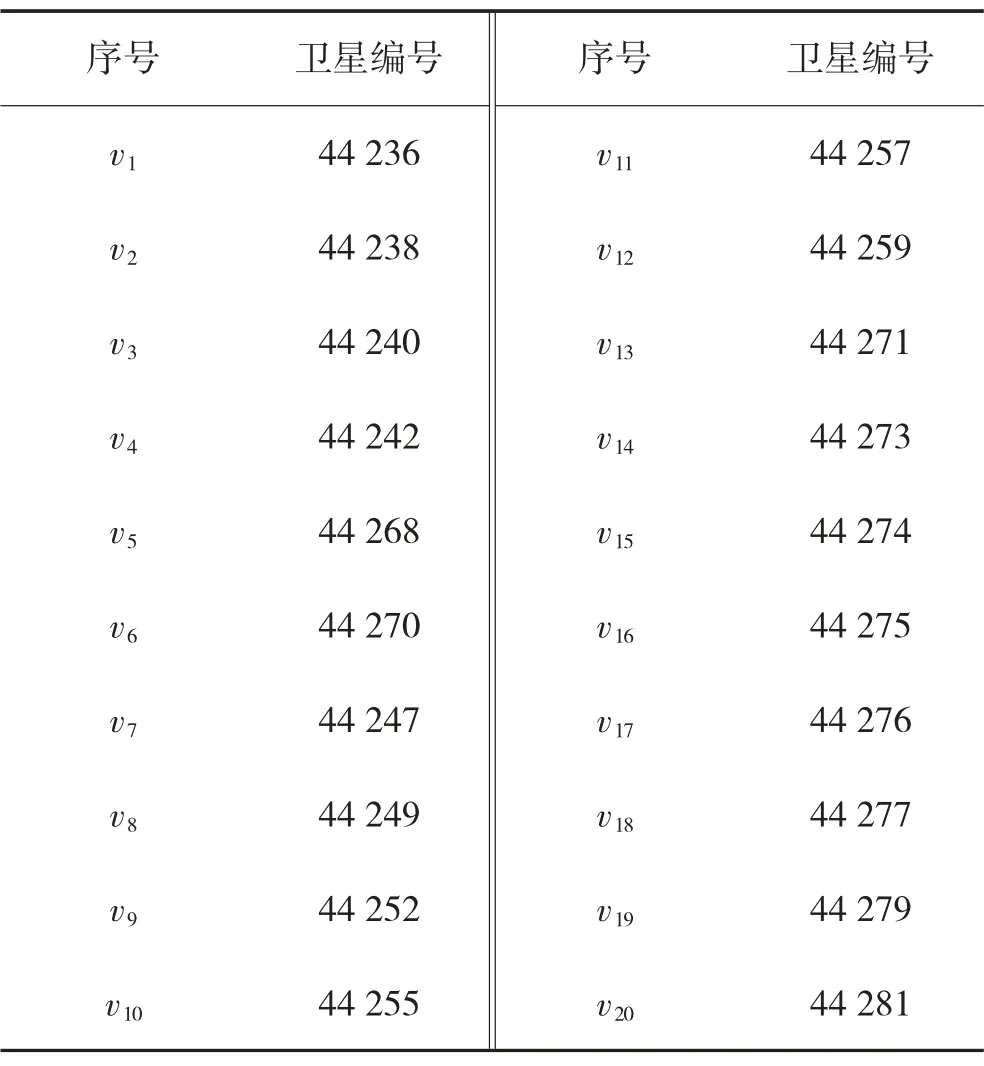
表1 卫星编号信息Table1 Number information of satellites

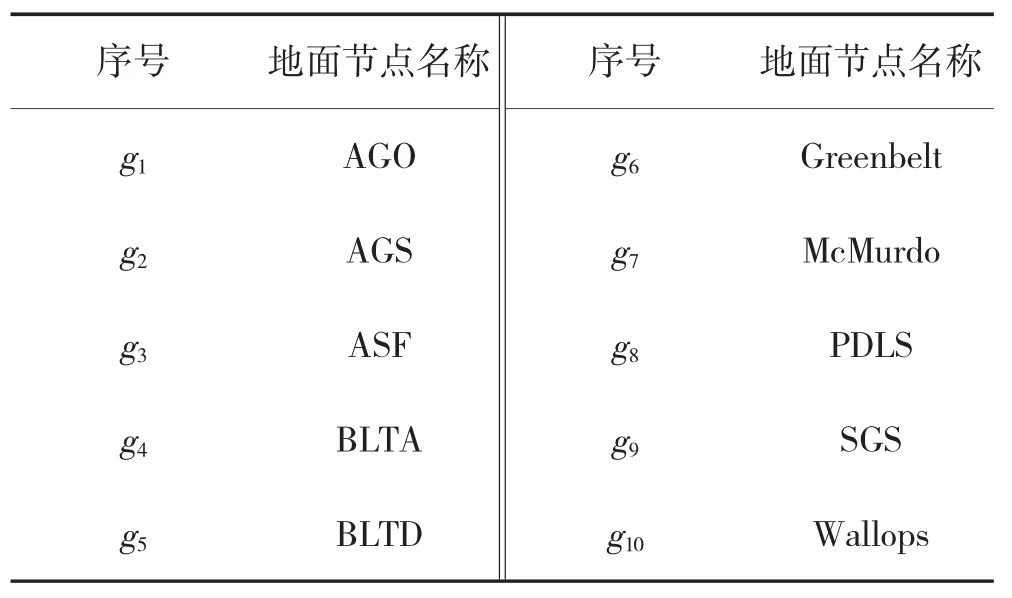
表2 地面节点名称Table2 Names of ground stations

4.1 DCDR 的时延性能仿真

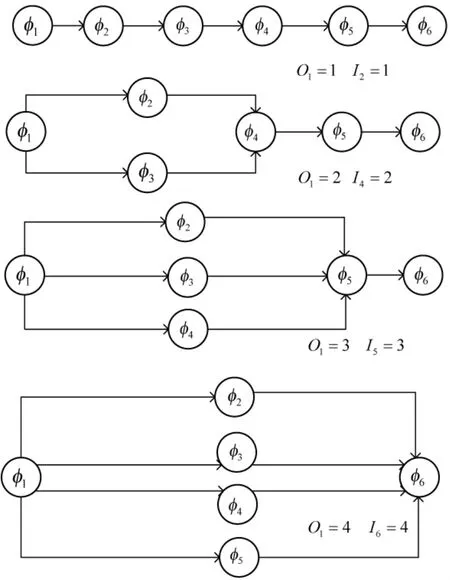
图4 任务DAGsFig.4 DAGs of task

通过图5 对DCDR 的性能进行分析, 不同任务DAG 对任务传输和计算的时延有较大的影响. 首先,任务执行的总时延不仅随着任务量的增多也增多,也随着任务的分支变多逐渐增加. 这是因为随着分支变多, 而这些分支需要映射到一条路径中, 增加了任务传输的负担. 在总的执行时延中, 计算时延所占的比重很大, 并且随着分支数目和任务量增加也增加. 因此, 在SGIN 场景中的DCDR 控制策略更加适合串行的任务, 并且在执行任务时, 计算时延在任务处理过程中起较为关键性的作用.

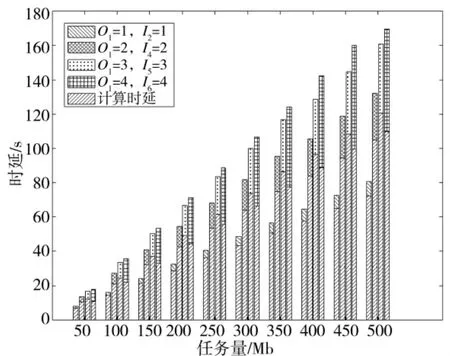
图5 不同任务DAGs 对时延的影响Fig.5 Effects of different DAGs on latency

如图6 所示, 对比了DCDR 与传统云计算之间的差异. 传统云计算需要接入卫星将任务传输至云计算中心, 然后将计算结果返回给目的卫星节点. 在这里, 选择了g6地面节点作为云计算节点, 计算能力为10 MHz. 发现针对O1=1 I2=1, O1=2 I4=2, O1=3 I5=3 的任务而言, 云计算由于其较长的星间和星地传输路径, 导致时延大于DCDR. 针对O1=4 I6=4, 随着并行分支变多, 这些分支需要映射到一条路径中, 增加了DCDR 中任务传输的负担, 导致DCDR 时延大于云计算. 因此, 针对并行分支较少的任务DAG 而言, DCDR 在降低任务总处理时延方面有较为明显的优势. 但是随着任务并行分支变多, DCDR 降低时延的效果一般.

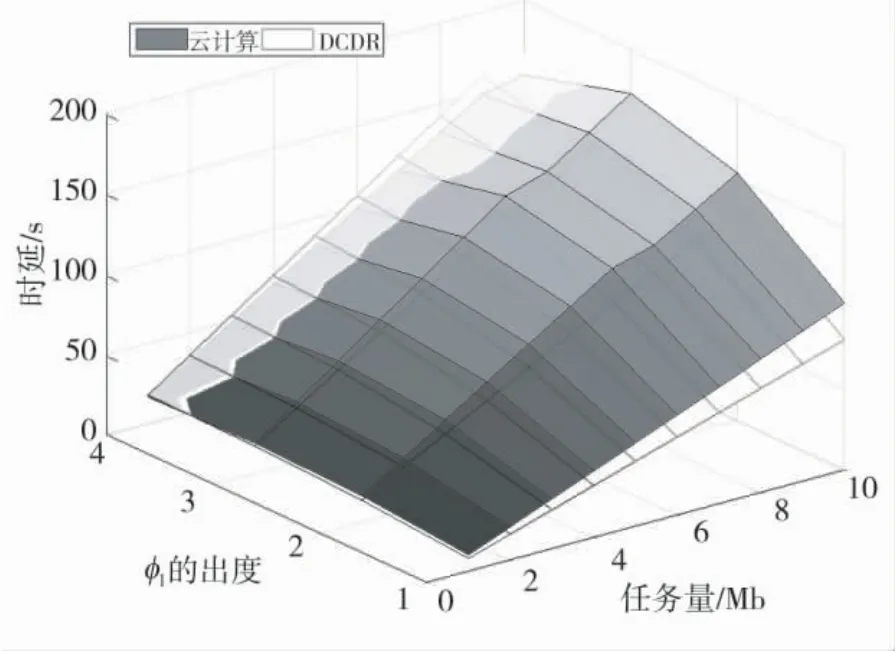
图6 DCDR 与云计算的时延对比图Fig.6 Latency comparison diagram of DCDR and cloud computing

4.2 DCDR 的冗余抗毁性能仿真

为了测试DCDR 的冗余抗毁性, 同时考虑了卫星和地面节点的意外损坏. 假定卫星和地面节点损坏的个数服从均匀分布, 即damage_num～U（[1, 10]）.每次算法运行的过程中随机毁坏1～10 个节点, 并且针对不同的损坏个数分别测试100 次实验, 计算其任务处理失败的概率. 如图7 所示, 以O1=1 I2=1 为例, DCDR 的失败概率明显低于采用固定传输路径的方法. 无中心分散式的DCDR 方法能够在选择路径的过程中动态规避毁坏的节点, 从正常工作的节点中重新规划下一跳的路径并映射计算, 从而达到有效提高DCDR 的抗毁性.

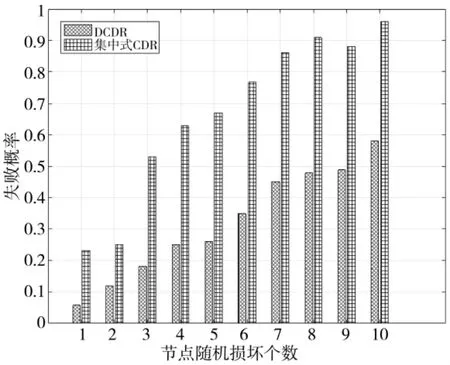
图7 DCDR 抗毁性分析Fig.7 Invulnerability analysis of DCDR

4.3 DCDR 映射结果展示

图8 给出两个不同的任务DAG 的映射结果和同一个DAG 不同任务量的映射结果. 通过图8（a）和图8（b）对比, 发现不同的DAG 会有不同的映射结果,这表示所提出的DCDR 方法可以适应不同任务DAG 模型得到不同的映射结果. 其次, 对比图8（a）和图8（c）, 发现对于同一个任务DAG 当任务的计算和传输时延超过的一个时隙的长度时, 会出现通过虚拟链路跨时隙的情况, 达到适应网络动态变化的效果.

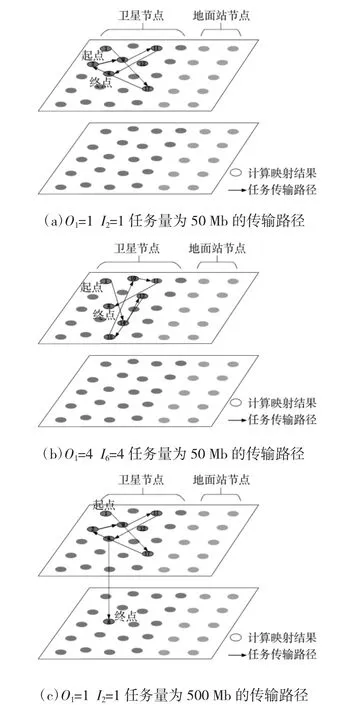
图8 不同任务DAG 相同任务量以及不同任务量相同DAG映射结果Fig.8 The mapping results of different DAGs with same size of task and different size of task with same DAG

5 结论

针对无中心、分布式、高动态的天地一体化网络中大规模端到端传输问题, 本文提出一种考虑计算映射与动态分布的DCDR 范式. 通过采用时空扩展图模型对动态网络进行了稳态化处理, 基于稳态化SGIN 设计改进的定向扩散算法实现最优DCDR控制策略制定. 仿真结果表明, DCDR 控制策略能够灵活高效地实现不同种类的任务的计算和传输, 适应SGIN 的动态变化及时调整传输路径, 并具有较好的冗余抗毁性. 下一步将考虑面向高中低轨道卫星、计算资源受限下的路由控制策略研究, 进一步优化模型及冗余抗毁性能, 以提高时延性能和路由效率.研究成果将为面向各类军事应用的天地一体化网络的高效联接和鲁棒传输, 提供理论方法和技术支撑.