巷道垮落煤散体宏细观力学参数相关性的实验研究

2022-02-17王楠楠

黑龙江科技大学学报 2022年1期

高霞，王楠楠，裴权

(黑龙江科技大学建筑工程学院，哈尔滨 150022)

0 引言

煤与瓦斯突出事故不仅影响煤炭行业的健康发展，还对社会和谐稳定造成一定影响。在煤矿井下灾害发生后，应急救援成为“最后一道防线”[1]。应急救援通道的再造是开展煤矿应急救援技术研究的一个重要内容。巷道垮落体固体介质主要有砂砾岩、砂岩、块体煤等[2]。深入了解煤岩散体力学性质对于垮落体内再造应急救援通道具有重要意义。直剪实验是测定煤岩散体力学性质较为快速的方法，但只能测得散体的宏观力学特性，无法获得试样内部颗粒间应力变化、运动规律以及从细观角度揭示其宏观变形机理[3]。近年来，离散元方法已成为通过改变颗粒及颗粒间细观参数来研究材料力学行为的有效途径[4-6]，材料宏细观参数的相关性研究是离散元数值建模的关键。

目前，国内外学者利用三轴实验[7-10]和直剪实验[11-14]研究了不同剪切速率、含水率、含石量、块石尺寸及形状等影响因素下散体强度变形等特征规律[15-16]。但大部分都是针对宏观力学特性研究，对其细观力学研究相对较少。基于此，部分学者利用离散单元法开展了散体细观力学实验研究。Wang等[17-18]采用PFC2D建立了人工胶结砂土的三轴排水压缩数值模型，分析了胶结对强度与体变特征的影响，并从细观层面揭示了人工胶结砂土特性变化的内在机理。马石城等[19]采用PFC3D软件建立了含有不同形状堆积碎石土三轴压缩数值模型，探讨了不同含水率下细观力学参数与强度指标的定量关系。史乃伟等[20]基于室内直剪实验与颗粒流软件建立了粗砂颗粒模型，从颗粒层面探讨了临界状态下颗粒运动规律。综上所述，目前学者们对于散体宏细观力学性质研究对象主要是土石混合体、人工胶结砂土及堆积碎石土，对煤岩散体的实验研究偏少，数值模拟实验亦鲜有研究。

笔者针对煤散体直剪实验，首先，建立煤散体直剪试验离散元模型；其次，进行细观参数标定与模型可靠性验证；最后，基于建立的模型分析接触有效模量Ec、刚度比η、摩擦因数μ等煤散体细观参数对剪切模量G和抗剪强度τf等宏观力学参数的影响，并确定其宏细观数学关系，为煤散体颗粒材料离散元模拟中细观参数标定提供借鉴。

1 离散元数值模型的建立

1.1 实验

文中试样来自黑龙江双鸭山双阳煤矿井下破碎煤散体，对试样进行1∶10(缩尺后模型颗粒粒径与原型颗粒粒径尺寸之比)缩尺处理[21-22]。在直剪盒尺寸为150 mm×150 mm×150 mm，法向应力分别为50、100、150、200 kPa，剪切速率分别为0.03、0.06、0.09 mm/s条件下，测定该煤散体抗剪强度、剪切模量。室内实验中煤散体密度为1.75 g/cm3，粒径范围2～25 mm。现场煤散体粒径，如表1所示，其中，w为某粒径范围煤粒的质量所占颗粒总质量的百分数。

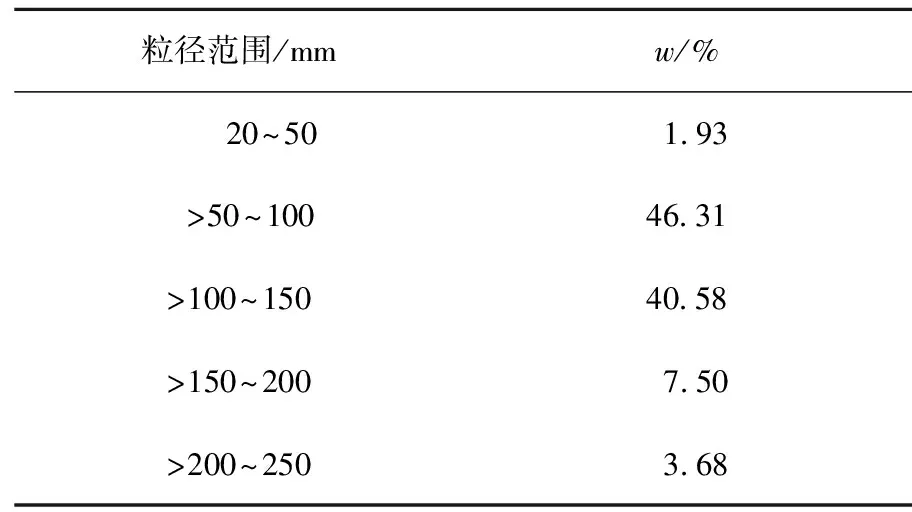
表1 煤粒粒径现场实测结果

1.2 直剪盒模型的建立

文中以煤散体为研究对象，数值模拟实验中剪切速率为0.06 mm/s，因其黏聚力c非常小，可不予考虑，故采用线性刚度接触模型较为合理。为了使数值模拟结果与实验结果吻合度更高，模拟实验采用的颗粒粒径范围、直剪盒尺寸与室内实验一致。

剪切盒尺寸与室内实验装置尺寸一致，均为150 mm×150 mm，该盒由8面墙组成。采用颗粒级配法生成剪切试样后，通过伺服程序施加法向力，使试样固结稳定。下盒固定不动对上盒进行剪切，保持法向应力不变，给上盒施以速度实现上下盒的相对运动，模拟煤散体直剪实验。直剪实验二维离散元模型示意图，如图1所示。室内实验与模拟实验中颗粒级配曲线对比见图2。

图1 直剪实验二维离散元模型Fig. 1 Two-dimensional discrete element model of shear test

图2 实验与模拟级配曲线对比Fig. 2 Comparison of gradation curves between test and simulation

1.3 细观参数的标定

根据散粒体弹性理论，当颗粒接触刚度的取值在108～109N/m之间、η在1～3之间时，模型收敛性良好[23]。参考金磊[24]、杨升等[25]学者所取参数，文中通过大量的参数调整测试标定细观参数，最终使得数值模型模拟结果和室内实验材料的力学响应基本一致，其细观参数见表2。其中，ξ为阻尼系数，k为孔隙率。图3为法向应力σn为100 kPa下的数值实验与室内实验的剪应力-剪位移曲线对比。

表2 模型细观参数

图3 剪应力-剪位移曲线对比Fig. 3 Comparison of shear stress-shear displacement curves

从图3中可以看出，数值实验剪应力-剪应变曲线形状与室内实验较吻合，两者均表现出明显的应变软化特征。此外，借鉴魏厚振等[26]对剪应变γ=0.02所对应的割线模量为剪切模量G的定义，计算了室内实验与数值实验所对应的剪切模量分别为1.89×103kPa和2.08×103kPa，两者误差为0.09，小于10 %。在100 kPa法向应力下数值实验达到剪应力峰值时，对应的剪切位移小于室内实验。这可能是由于数值模型中的材料刚度大于实际材料造成的[27]。

总体而言，标定的细观参数能够满足数值实验的精度要求，为准确地分析细宏观参数之间的关系提供了前提条件。

2 细观参数对宏观力学性质的影响

影响煤散体宏观力学性质的因素众多。内因方面有煤散体的组成、结构与状态[28](散体颗粒大小、级配、形状、黏结力、孔隙比、密度、刚度、摩擦因数等)；外因有应力状态、应力历史、加载条件(围压与加载速率)、试样尺寸及温度等。文中在法向应力σn为100 kPa条件下，对每种细观参数(如接触有效模量、刚度比及摩擦因数)进行10组实验。由于篇幅所限，每组实验仅列出5组剪应力-剪位移曲线。

2.1 接触有效模量

颗粒接触有效模量主要影响颗粒体系的弹性模量[29]。保持η=1.0、μ=0.5不变，Ec介于2～26 MPa(共10组)，探讨接触有效模量下数值实验煤散体剪应力-剪位移曲线如图4所示。10组接触有效模量Ec下数值实验煤散体的抗剪强度τf和剪切模量G值见表3。法向应力为100 kPa时，Ec-G/τf的关系如图5所示。

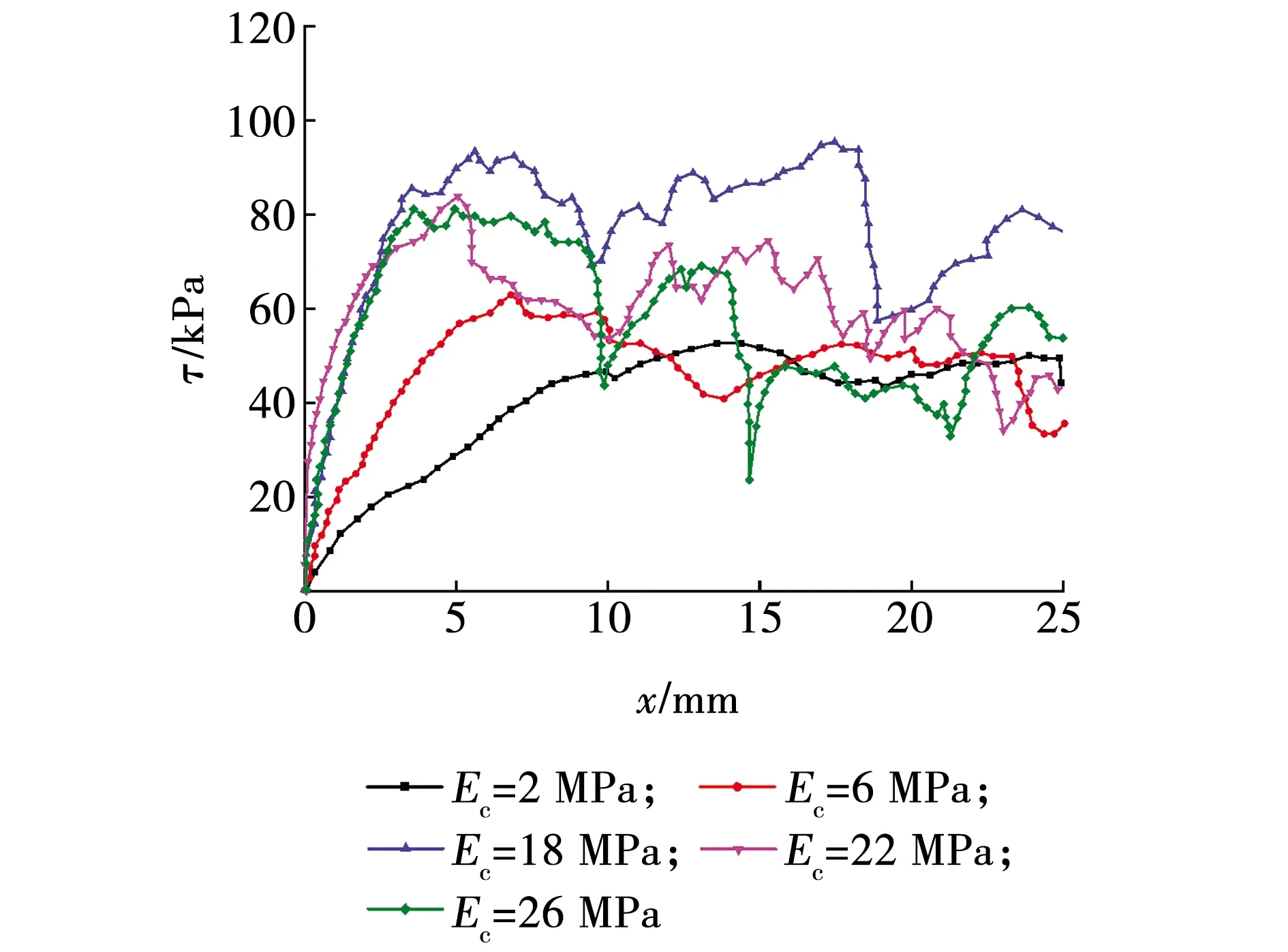
图4 不同有效模量下煤散体剪应力-剪位移曲线Fig. 4 Shear stress and shear displacement of coal dispersion under different effective modulus

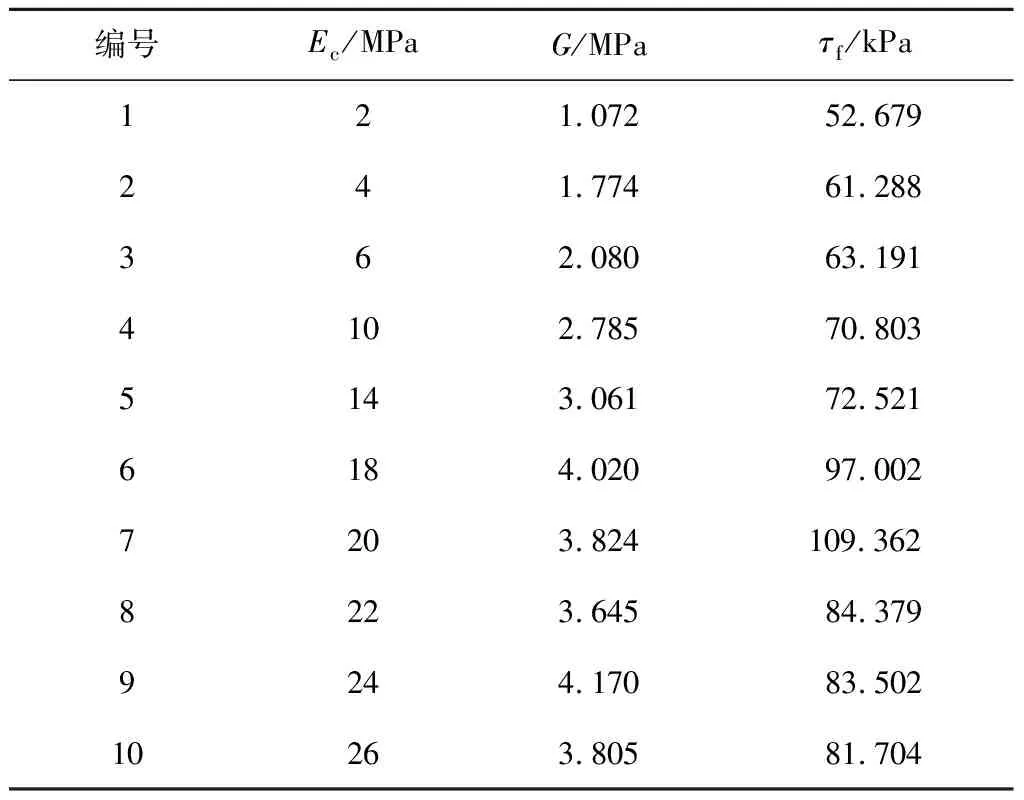
表3 不同有效模量下的剪切模量与抗剪强度

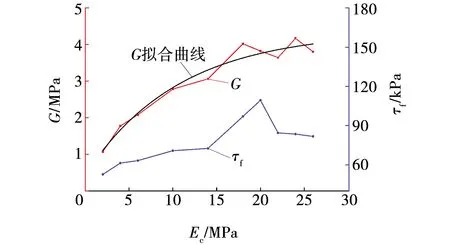
图5 剪切模量、抗剪强度与有效模量的关系Fig. 5 Relationship between effective modulus, shear strength and shear modulus

由表3与图5可以看出，当接触有效模量Ec在0～20 MPa之间变化时，剪切模量G和抗剪强度τf均随接触有效模量Ec的增加而增加，且抗剪强度增速较慢。当接触有效模量Ec在20～26 MPa之间时，剪切模量G随接触有效模量Ec的增加先减小再增加最后再减小；抗剪强度τf随接触有效模量Ec的增加而减小。整体来说，剪切模量随着接触有效模量的增大总体呈增大趋势，两者近似呈指数正相关；抗剪强度随着接触有效模量的增大总体呈增大趋势。剪切模量G与接触有效模量Ec拟合函数为

G=4.356-3.921 exp(-0.094Ec)。

(1)

二者相关系数R2=0.953 9，分析认为，接触有效模量越大，颗粒抵抗变形的能力越强，颗粒发生剪切滑移所需外力就越大[30]，试样宏观剪切模量与抗剪强度就越高。

2.2 刚度比

颗粒的刚度比主要影响颗粒体系的泊松比[29]。保持Ec=6.0 MPa、μ=0.5不变，η介于0.2～4.5(共10组)，探讨不同刚度比下数值实验煤散体剪应力-剪位移曲线，如图6所示。10组刚度比η下数值实验煤散体的剪切模量G及抗剪强度τf值见表4。法向应力为100 kPa时，η-G/τf的关系如图7所示。

图6 不同刚度比下煤散体剪应力-剪位移曲线Fig. 6 Shear stress and shear displacement of coal dispersion under different stiffness ratios

表4 不同刚度比下的剪切模量与抗剪强度

由表4与图7可以看出，剪切模量G在随η增大的过程中虽出现有增大现象，但整体上随η的增加而减小，两者近似呈指数负相关，相关系数R2=0.972 4，其拟合关系式为

(2)

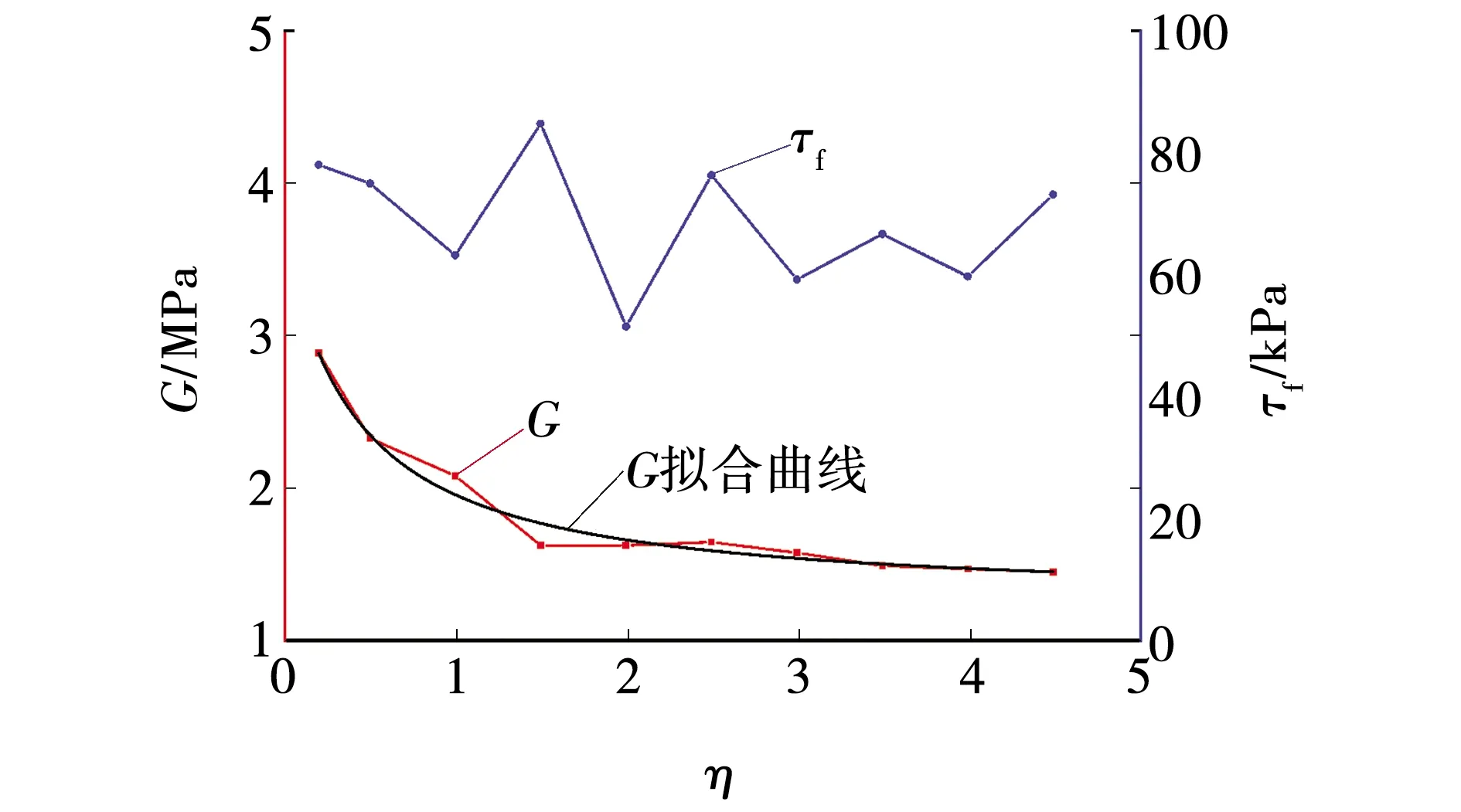
图7 剪切模量、抗剪强度与刚度比的关系Fig. 7 Relationship between stiffness ratio,shear modulus and shear strength

抗剪强度τf随η的增加呈波动变化，变化范围为51.509～84.780 kPa，呈上下波动，且无明显规律。这与荆鹏[31]研究刚度比对粒状土强度特征的影响结果相一致。分析认为：在接触有效模量不变时，刚度比变化主要影响颗粒的切向刚度；随着刚度比增大，切向刚度逐渐减小，导致在相同外载作用下颗粒切向变形增大，宏观上表现为煤散体试样剪切模量减小。抗剪强度随刚度比出现上下波动，分析认为，抗剪强度可能受孔隙率与切向刚度共同影响，具体影响机制有待进一步研究。

2.3 摩擦因数

颗粒摩擦因数主要影响颗粒体系的抗剪强度[29]。保持η=1.0、Ec=6.0 MPa不变，摩擦因数μ介于0.1～1.0(共10组)，探讨不同摩擦因数μ下数值实验煤散体剪应力-剪位移曲线如图8所示。10组摩擦因数μ下数值实验煤散体的剪切模量G及抗剪强度τf值见表5。法向应力为100 kPa时，μ-G/τf的关系如图9所示。

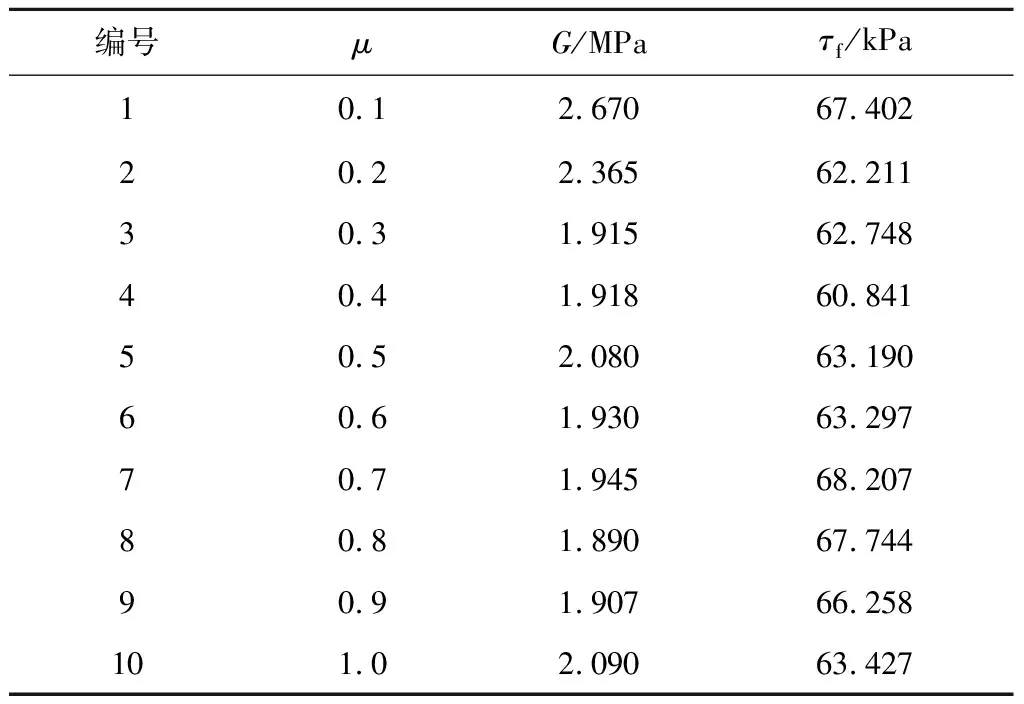
表5 不同摩擦系数下的剪切模量与抗剪强度

图8 不同摩擦系数下煤散体剪应力-剪位移曲线Fig. 8 Shear stress and shear displacement of coal dispersion under different friction coefficients

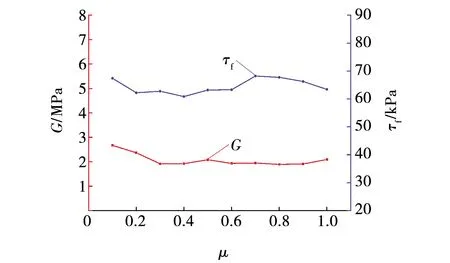
图9 剪切模量、抗剪强度与摩擦系数的关系Fig. 9 Relationship between friction coefficient, shear modulus and shear strength

由表5与图9可以看出，剪切模量G随着摩擦因数μ的增大先减小后逐渐趋于稳定，变化范围为1.890～2.670 MPa，摩擦因数μ对其影响较小。抗剪强度τf随摩擦因数μ增加无明显变化规律，变化范围为60.841～68.207 kPa，抗剪强度τf差值在10 kPa以内。通过实验进一步得到摩擦因数μ为0时，抗剪强度τf为60.463 MPa，剪切模量G为2.593 MPa，表明摩擦因数μ对抗剪强度τf影响较小。这与王鹏[32]、张志华[33]研究的摩擦因数对散粒体强度特征的影响结果一致。