Surf结合区域生长的特征点提取改进算法

2022-02-17李忠勤宋虎虎周海超

黑龙江科技大学学报 2022年1期

李忠勤，宋虎虎，周海超

(黑龙江科技大学电气与控制工程学院，哈尔滨 150022)

0 引言

特征点提取一直是图像特征匹配研究领域的重点，而Surf算法是图像特征点提取的常见方法之一。毛克乐[1]提出一种基于改进Surf和Delaunay三角剖分图像匹配算法，解决了Surf引起的颜色成分信息丢失和特征点过于密集问题。吴清辉[2]利用DAISY算法生成的描述子替代Surf算法中描述子的方法提高了模板匹配算法精度与实时性。徐瑞瑞等[3]提出了SurfGPU算法，其像元精度提取准确率比Surf算法提高了7%。徐启文等[4]提出一种动态阈值的方法，通过缩小特征点提取区域的方法实现特征匹配。戴雪梅等[5]给出一种结合ORB与Surf的SURF-ORB算法，实现了特征点匹配速度快和准确率高的效果。刘强[6]指出一种长距离特征点拼接提取算法，提高了边缘检测效率。黄易豪等[7]采用Gabor滤波与对比度受限的自适应直方图均衡算法相结合，以增强图像与分割图像，提升了特征点的识别率。罗兴潮等[8]提出用RANSAC算法筛选匹配点，使Surf特征点匹配具有较高的精度与计算效率。彭明君等[9]采用局部差异二值(LDB)描述子描述特征点区域，有效提高了特征点提取效率，以及图像拼接的快速性和成功率。

基于上述分析，对于边缘光滑物体的图像，Surf算法提取特征点能力较弱，学者们并没有给出很好的解决方法。考虑到区域生长算法具有分割图像特征区域的能力，笔者拟结合区域生长算法与Surf算法，即Surf-RGA算法，用于图像特征点提取，以提取篮球表面LOGO及线条等特征点为例，借助Matlab软件实现图像仿真实验，验证所提方法的正确性及可行性。

1 区域生长算法的改进

区域生长算法是一种将性质接近的像素点集聚在一起的图像分割方法[10]。文中选取了常见的斯伯丁篮球，篮球表面具有边缘光滑的特点，可满足仿真实验条件。

传统区域生长算法是通过鼠标手动选取种子点，由于完全依赖实验人员主观意愿选择，致使种子点的选取具有主观性，图像分割效果较差；同时，手动选取种子点费时费力，图像分割效果较差，不连通区域无法被分割出来[11]，如图1所示。

图1 分割较差图像Fig. 1 Poorly segmented images

基于此，对区域生长算法进行改进，采用局部平均值判断法，将预处理后的整个图像分成 3×3矩阵形式，产生9个区域。最后，计算每个矩阵区域内像素点的平均值Q，并选取均值最大的矩阵J。

Qi=xi/9，i=1，2，…，9，

J=max{Qi}，i=1，2，…，9，

式中：xi——第i个区域像素点值；

Qi——第i个区域像素点平均值；

J——均值最大的矩阵。

将矩阵J作为中心点，由此开始向邻域生长，该方法便可实现种子点自动选取，获得效果较好的分割图像，如图2所示。

图2 分割较好图像Fig. 2 Well segmented image

2 Surf算法

Surf算法是对两组图像进行特征点描述与匹配的方法[12]，其算法稳定性较好且运算快，算法流程如图3所示。

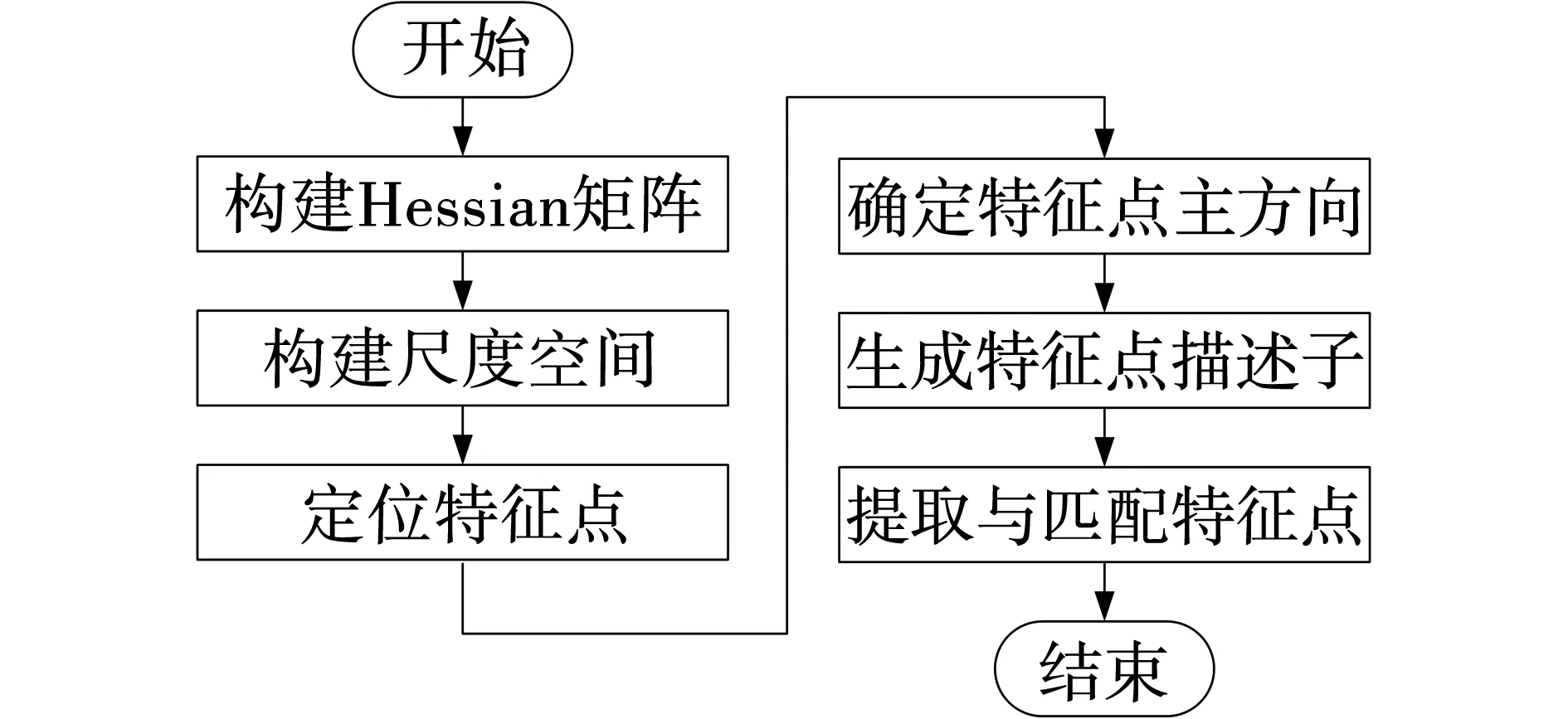
图3 Surf算法流程Fig. 3 Surf algorithm flow

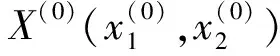
(1)

将式(1)写成矩阵形式，即

且

f(X)=f(X(0))+∇f(X(0))TΔX+

(2)

因此，

G(X(0))即为f(x1,x2)在X(0)点处的Hessian矩阵，运用Surf算法处理一个图像f(x,y)时，其Hessian矩阵为

3 仿真与结果分析

3.1 仿真流程

为验证Surf-RGA算法可行性，在Matlab 2019a软件平台下进行仿真实验，仿真过程见图4。

图4 实验仿真流程Fig. 4 Experimental simulation process

3.2 实验过程

为使实验图像具有说服性，选择两种不同色彩且图标位置不同的篮球图像，如图5所示。

图5 原始图像Fig. 5 Original image

根据仿真实验流程，灰度化处理输入的图像，转换为无色彩的灰度图像，中值滤波去除噪声，如图6所示。

图6 去噪后图像Fig. 6 Image after denoising

设定区域生长的阈值为28、种子点的循环次数为12，循环次数表示种子点个数，经过区域生长改进算法处理的图像，如图7所示。

由图7可见，图像表面带有杂点，这是由于拍摄图片表面曝光的影响。为解决此影响，将区域生长的阈值设为28和10，设置种子点的循环次数为13和12，得到清晰图像如图8所示。其为图像特征点提取提供便利。

图7 未改正分割图像Fig. 7 Uncorrected segmented image

为去除经过区域生长改进算法处理的图像噪声影响，在Surf算法之前，采用最大值法将图像预处理，如图9所示。

图8 改正后分割图像Fig. 8 Segmented image after correction

图9 最大值法处理后图像Fig. 9 Image processed by maximum method

此时，由式(2)可知，图9中图像的高斯卷积为f(x,y)，其Hessian矩阵为

图像经过高斯滤波后的Hessian矩阵表述为

由于图像的相邻像素在离散型数字分析计算过程中，有一阶导数灰度差公式为

Lx=L(x+1,y)-L(x,y)，

二阶导数为

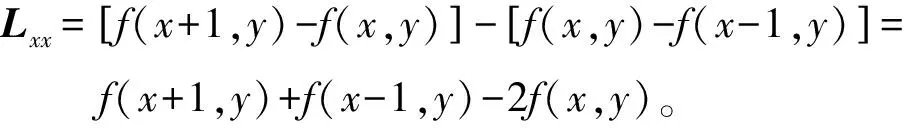
此时，Hessian矩阵的判别式为

detH=LxxLyy-LxyLxy。

为提高运算速度，引入盒式滤波器，同时为了消除此过程产生的误差，添加参数γ，文中γ=0.9，则有

detH=LxxLyy-(γLxyLxy)2，

即

detH=LxxLyy-(0.9LxyLxy)2。

detH取得局部极大值时，程序自动将当前点与周围邻域内其他更亮或更暗的点进行比较，由此来定位特征点的位置。

对特征点主方向的确定，同样，计算Harr小波特征总和mω，由于图像特征点区域已经分割，因此，以90°扇形将特征点的圆形邻域分成四个区域，分别统计四个区域内Harr小波特征总和mω之后，选取Harr小波特征值最大的扇形方向θ作为该特征点的主方向，特征总和的计算公式为

θω=ω，

θ=θω|max{mω)，

式中：mω——ω方向Harr小波特征总和；

ω——45°、135°、225°、315°；

θω——ω方向特征点所在角度；

θ——特征的主方向角度。

因此，可得特征点方向生成示意图，如图10所示。Surf算法处理结果如图11所示。

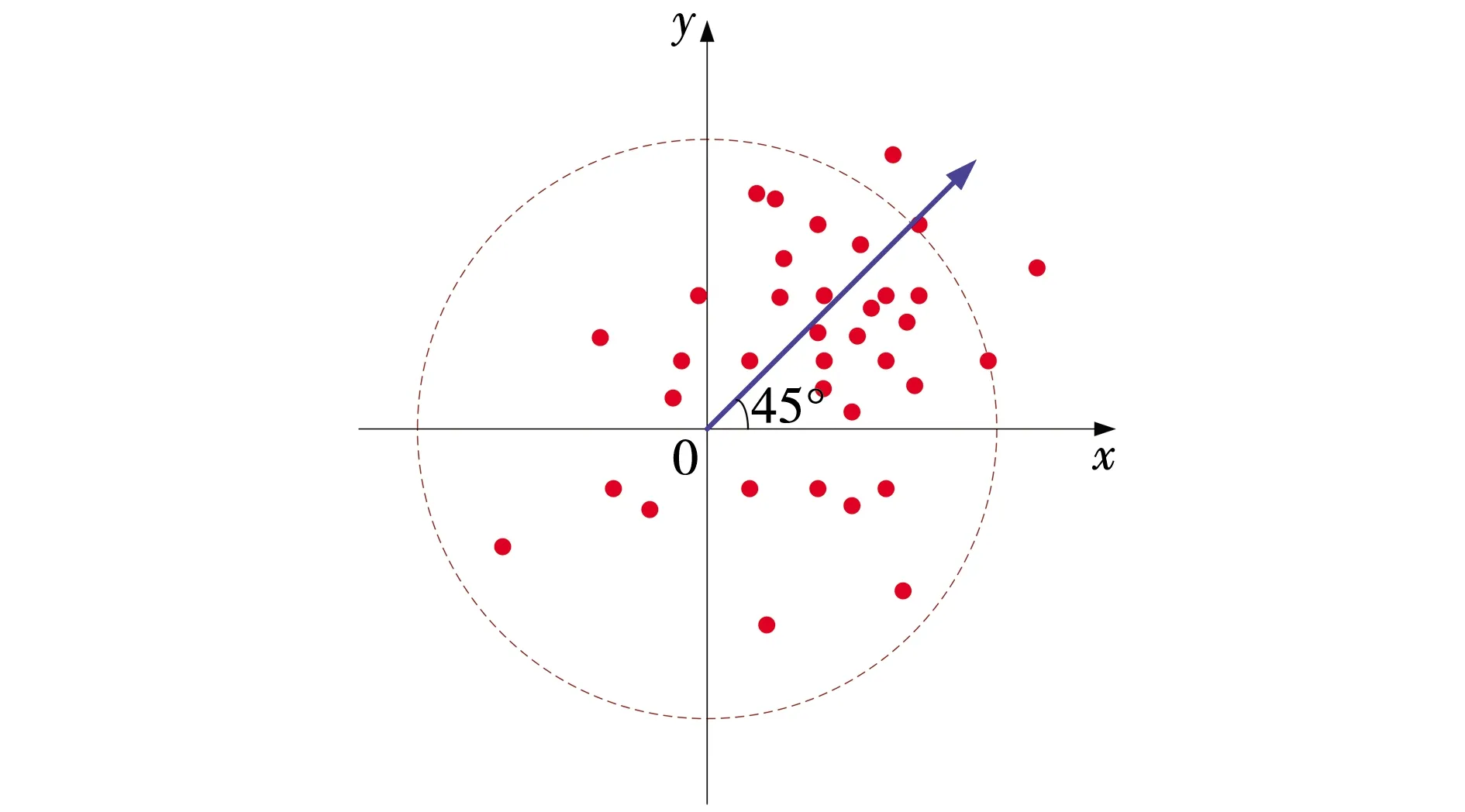
图10 特征点方向生成示意Fig. 10 Generation of feature point directions

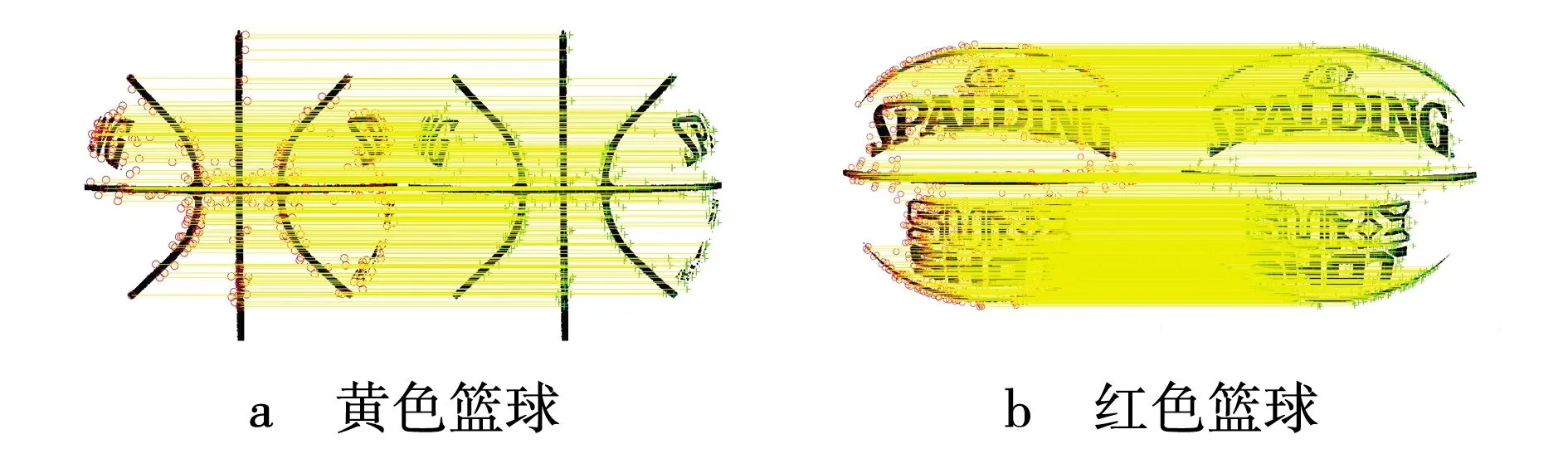
图11 Surf算法处理后图像Fig. 11 Images processed by Surf algorithm

为方便对比分析Surf算法与Surf-RGA算法提取图像特征点的能力，实验将没有经过区域生长处理的原图像单独进行Surf算法处理，如图12所示。

图12 Surf算法对原始图像处理Fig. 12 Surf algorithm for original image processing

3.3 仿真结果分析与验证

为避免选取图像的偶然性，又随机选取10组不同角度的篮球图像进行验证，特征点数量数据对比结果如表1所示。

表1 特征点数量数据对比

由表1可知，在算法演算过程中，可能陷入局部最优解，因此，排除表1中图像12异常数据。图像分别经过Surf-RGA算法与Surf算法处理后，特征点提取数量明显不同，前者中图像特征点提取数量明显提高至原来的多倍，特征点增加率的平均值约达到了420.69%。

为了更直观比较特征点变化，将图像表面特征点待识别提取区域按由简单到复杂排列，特征点数量变化折线如图13所示。

图13 特征点数量变化Fig. 13 Number of feature points changes

由图13可知，从横轴上比较，在图像表面特征点待识别提取区域由简单到复杂的过程中，Surf算法提取的特征点数量逐渐增多，呈现递增趋势；Surf-RGA算法提取特征点数量虽然表现出起伏不平，但是整体上呈现递增的趋势。从纵轴来看，Surf-RGA折线位于Surf折线上方，两者特征点提取能力Surf-RGA方法明显优于Surf算法。