侧限条件下充填散体与岩柱相互作用机理
2021-01-15勒治华于庆磊郑浩田曹永胜
勒治华, 于庆磊, 郑浩田, 曹永胜
(东北大学 资源与土木工程学院, 辽宁 沈阳 110819)
充填采矿技术在控制采场地压、预防深井岩爆、防止采场变形、提高矿石回收率、保护生态环境等方面具有显著的作用[1-4].但由于充填体刚度远小于其置换矿体的刚度,充填后采场围岩并未处于真正平衡态,导致了矿柱(围岩)与充填体之间存在相互作用,充填体的作用机理和这种相互作用关系是影响空区围岩稳定的重要因素之一.
在充填体作用机理方面,Blight等[5]将圆柱形岩石试件置于钢筒中心并进行充填,对试件进行轴向压缩试验,并与没有充填材料包围条件下的岩石强度进行对比,揭示充填体的作用机理.采场内的充填体将矿柱(围岩)单轴或双轴的应力状态改变成三轴应力状态,限制其变形与位移的发展,从而增强了矿柱(围岩)的支撑能力.Heib等[6]和Zhang等[7]通过现场监测和数值模拟的方法,发现充填体会对矿柱和围岩提供一定侧向支撑作用.充填体的刚度对维持矿柱或围岩稳定性有重要影响,无论是胶结充填体还是非胶结充填体回填,矿柱的强度均会增大,但胶结充填体约束时矿柱强度提升效果更优[8-11].
在充填体与围岩相互作用方面,随着矿柱(围岩)变形程度越来越大,充填体与矿柱(围岩)之间的相互作用也越来越强烈[12].蔡嗣经等[13]从胶结充填材料及碎裂岩体的力学特性出发,研究了胶结充填采场围岩与充填体相互力学作用,并建立了相应理论模型;基于此,宋卫东等[14]在室内进行胶结充填体-岩柱组合结构侧限压缩实验,得到随着充填体强度的增大,岩柱的峰值强度、残余强度和破坏时的轴向应变均增大.通过数值方法,Tesarik等[15]发现充填体对破坏后的矿柱同样具有约束作用,充填体内部应力状态是其与围岩相互作用的结果;Falaknaz等[16]和Li等[17]发现充填体与围岩的相互作用会对充填体内的应力分布产生影响.
胶结充填以及高浓度充填代表着充填采矿技术的发展方向,但是在上向充填采矿中,水砂充填和干式充填占有相当的比重[18],有利于处理矿山长期积存的固废.因此,干式充填采矿法中,废石、尾砂等固废散体充填体的作用机理及其围岩相互作用关系对于维持空区稳定尤为重要.本文考虑充填散体结构特征,利用自制试验装置模拟干式充填采矿法中充填散体对矿柱的侧向支撑作用,进行散体约束下岩柱轴向压缩试验,分析充填散体对岩柱的作用机理,以及散体粒径对岩柱与充填散体相互作用影响,建立其相互作用过程中矿柱的承载模型,为指导矿山废石、尾矿等散体材料充填采矿提供重要理论支撑.
1 充填散体约束下岩柱轴向压缩试验
1.1 试验装置
充填散体侧向约束下岩柱轴向压缩试验系统主要由自制散体约束装置、应变采集单元、岩柱轴向加载单元三部分组成.如图1所示,散体约束装置为薄壁圆筒状,内径360 mm,筒壁厚度为2 mm,具有良好的抗压、柔韧性能;岩柱置于装置中心位置,充填散体置于筒壁和岩样之间,且在轴向方向被上、下环状浮动板约束;充填散体因岩柱变形挤压而侧向膨胀,为获得充填散体对筒壁的挤压环向变形,在装置外壁的3个高度水平位置处粘贴应变片(岩柱高度范围内),通过应变采集设备采集试验中环向变形数据;采用YAW-5000的微机控制电液伺服压力机配合散体约束岩石轴向压缩测试装置,选用0.5 mm/min的加载速率对岩柱进行轴向加载.
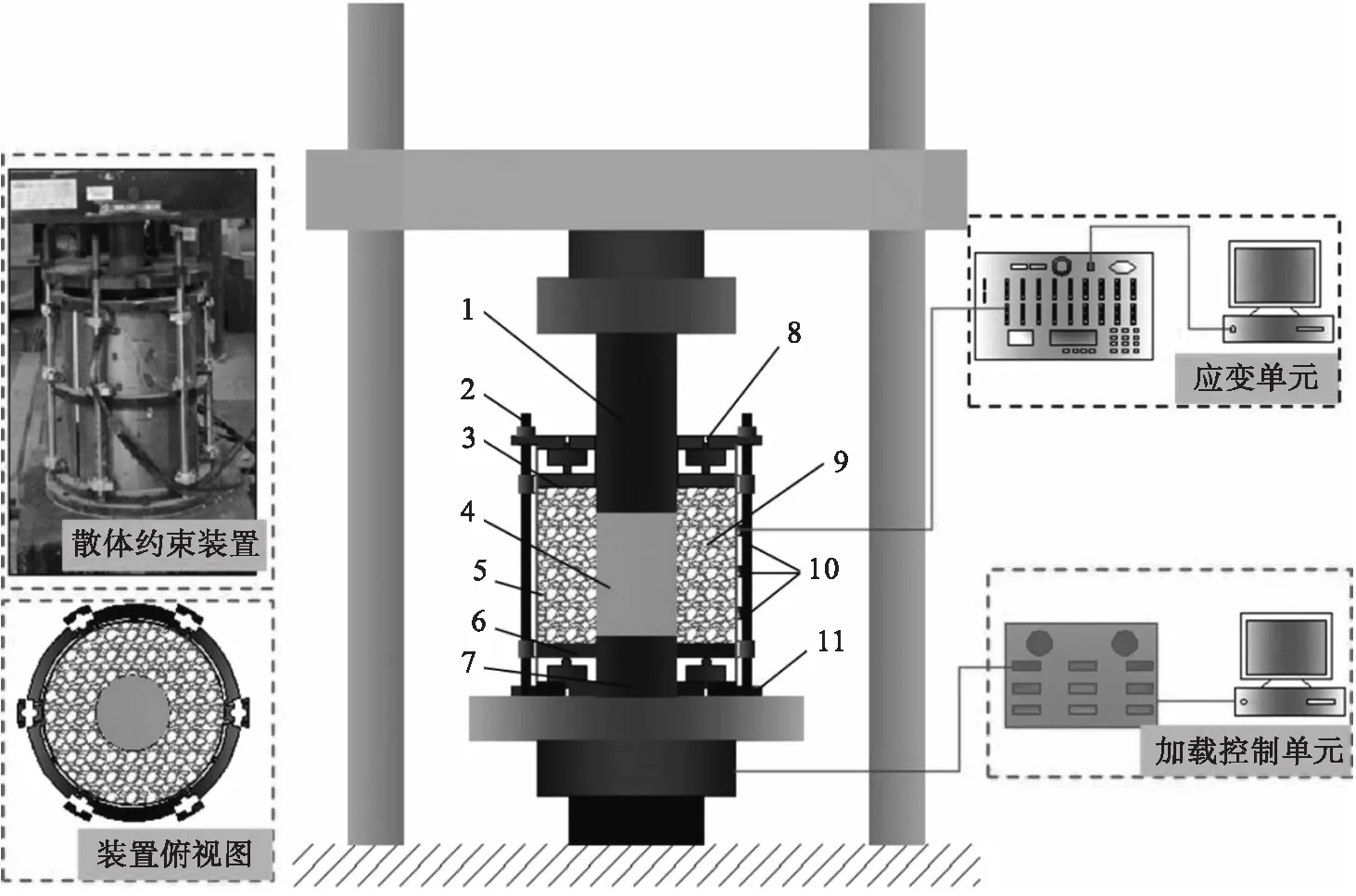
1—上传力杆; 2—螺杆; 3—上环状浮动板; 4—岩样; 5—筒壁; 6—下环状浮动板; 7—下传力杆; 8—可调节环状平板; 9—充填散体; 10—应变片; 11—固定环状板.
1.2 试验过程
本文选用直径为100 mm,高度为200 mm砂岩试件.采用非金属超声检测仪对96块符合ISRM试验要求的试件进行波速测量,选取波速较集中的砂岩试件进行单轴压缩和充填散体侧向约束下岩柱轴向压缩试验.充填散体采用河卵石,密度为2.678 3 g/cm3.利用标准分级筛对其进行分级处理为以下6组粒级:4.75~9.5 mm,>9.5~13.2 mm,>13.2~16 mm,>16~20 mm,>20~26.5 mm,>26.5~31.5 mm.
按照试验要求放置岩柱,分层装填河卵石,将试验装置置于YAW-5000的微机控制电液伺服压力机的加载平台上,加载中心线与岩样中心线重合,进行上述6组不同粒级充填散体约束下岩柱轴向压缩试验,岩柱单轴压缩作为对比试验.值得注意的是,每次试验结束后重新筛分河卵石,去除已被挤压破碎的河卵石.每种工况进行3次重复试验,取试验结果平均值分析.装置外壁应变采集系统与岩柱轴向加载系统同步进行.
2 试验结果与分析
2.1 充填散体作用机理
如图2和表1所示,充填散体的约束作用有利于岩柱强度的提高(值得注意的是,在>20~26.5 mm粒度充填散体约束下岩柱峰值强度增长幅度异常,这种现象可能与散体的堆积结构有关).相比于岩柱单轴压缩,在不同粒级充填散体约束作用下,岩柱峰值强度增长率为5.06%~19.31%,峰后残余强度保持在至少5 MPa以上(图2),表明充填散体对岩柱有类似围压作用.
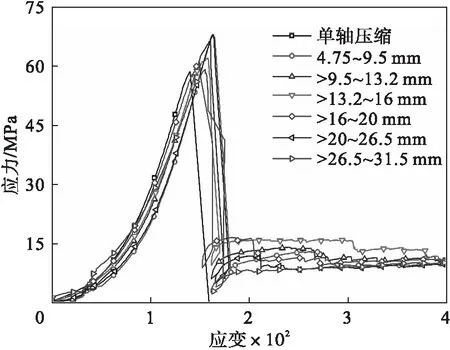
图2 不同粒级充填散体约束下岩柱应力-应变曲线
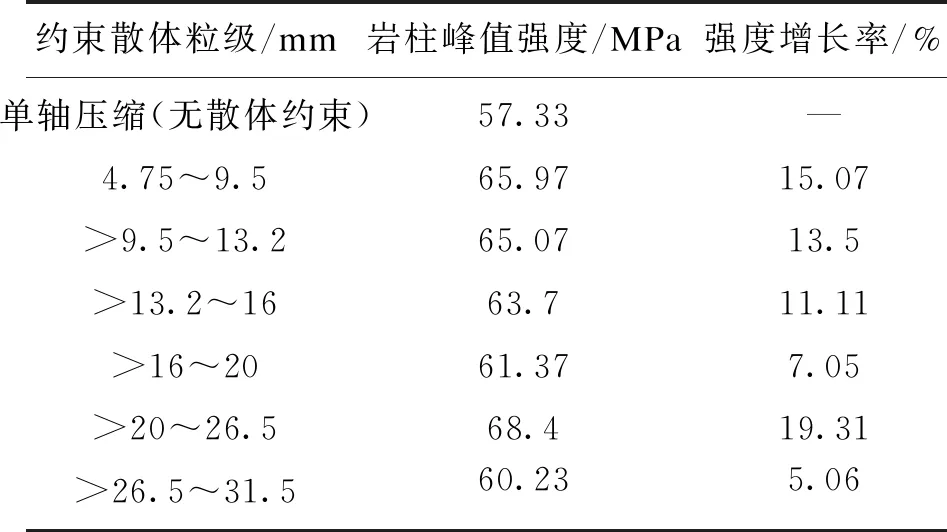
表1 充填散体约束下岩柱峰值强度
6组充填散体约束下岩柱轴向应力和散体挤压装置内壁产生的环向应变随时间变化趋势基本一致,以4.75~9.5 mm,>16~20 mm和>26.5~31.5 mm粒径约束为例,如图3所示,图中右侧为左侧岩柱峰值强度附近局部放大图.可知,在岩柱峰值强度之前某一时刻,装置外壁上的环向应变突然上升,即在岩柱即将到达峰值应力发生破坏时,岩柱变形挤压充填散体,充填散体对装置内壁挤压,致使环向应变突增;同时散体反作用于岩柱,产生被动的类似围压作用,使岩柱峰值强度提高;岩柱峰后阶段,继续对岩柱施加轴向压力,岩柱侧向变形对充填散体的挤压作用逐渐增大,其环向应变逐渐增大,充填散体对岩柱提供类似围压作用的被动压力也逐渐增大,阻止其进一步变形,增强其残余抗压强度.因此,充填散体对岩柱提供被动侧向支撑作用.
矿柱破坏模式受其受力状态影响[19].由图4可以看出,单轴压缩时岩样伴有侧面劈裂拉伸破坏,沿主裂纹方向出现了许多扩展裂纹;在充填散体约束条件下,岩样均以单斜面剪切破坏为主,岩样表面没有表现出明显的劈裂拉伸破坏.再次表明充填散体改善了岩柱的受力状态.
2.2 充填散体粒径对岩柱与散体相互作用影响
充填散体与岩柱的相互作用贯穿充填散体约束下岩柱轴向压缩整个过程,岩柱轴向应力峰后阶段更为显著,两者相互作用强度越大,充填散体对岩柱的约束作用越大,即残余强度越大.
与常规三轴试验中主动围压作用不同,本试验中的被动围压作用受充填散体的空隙率影响,充填散体与岩柱相互作用增强的过程实质上是充填散体颗粒之间空隙压密(空隙率减小)的过程,在此过程中,受充填散体颗粒之间摩擦、移动影响,被动围压作用不稳定,使得岩柱残余强度波动变化,如图2所示,峰后轴向应力随轴向应变呈“阶梯式”升降变化趋势.因此,分别选取轴向应变为0.028,0.033和0.038时对应的残余抗压强度进行分析,如图5所示,岩柱残余抗压强度随约束散体粒径增大呈先增后减的变化趋势,即粒径为>13.2~16 mm时,岩柱残余抗压强度最大,粒径为4.75~9.5 mm和>26.5~31.5 mm时,岩柱残余抗压强度较小,这主要与充填散体结构和变形有关.当约束散体粒径较小时,由于颗粒圆滑、流动性较强,充填散体颗粒骨架强度较低,相互作用过程中对岩柱提供的被动围压作用较弱;对于大粒径约束散体,虽然其颗粒棱角更加明显、流动性较差,充填散体颗粒骨架强度较高,但是充填散体之间空隙较大,挤压变形基本上被孔隙空间吸收,相互作用过程中无法对岩柱提供较强的被动压力.
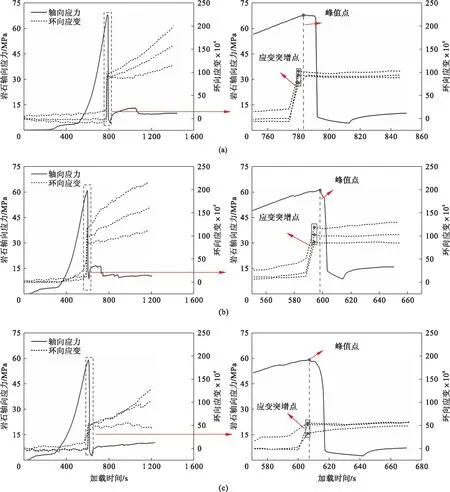
图3 充填散体约束下岩柱轴向应力和内壁环向应变随加载时间变化关系

图4 不同粒级充填散体约束下岩柱破坏形式
在岩柱与充填散体相互作用过程中,由于散体对岩柱的挤压,岩柱表面压痕(白点)明显,如图6所示.散体与岩柱表面为点-面接触,随着约束散体颗粒粒径增大,岩柱表面的压痕逐渐变稀
疏,且压痕越来越明显.这是因为在相同岩柱接触面上,散体颗粒粒径越大,接触面上颗粒数量越少,所以岩样表面的压痕越稀疏,但是点接触越少(接触面积越小),应力集中程度越高,因此压痕越明显.
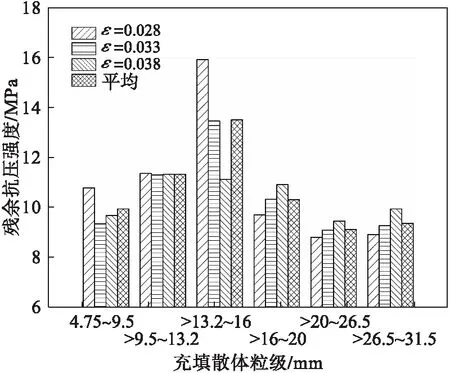
图5 岩柱残余抗压强度随充填散体粒级变化关系

图6 不同粒级充填散体对岩柱表面的挤压作用
2.3 相互作用力学模型
该试验过程可视为充填散体侧限条件下岩柱承载系统,与实际工程中废石、尾矿等散体充填体填充采空区相似,由于充填散体对围岩、矿柱的侧向支撑作用,增强了其抗压强度,对维持空区稳定性有重要意义.
矿柱在充填散体约束下的承载力学模型如图7所示,矿柱抗压强度σ1,充填散体对矿柱提供的围压为σ3,矿柱轴向应变ε和矿柱对散体侧向挤压应变εg.模型假设条件有:①采场充填完全接顶,且上覆岩层压力全部作用于矿柱;②充填散体因矿柱弹性变形而只产生侧向挤压变形;③矿柱处于极限应力平衡状态.则矿柱的应力和扩容侧向应变的表达式[20]:
(1)
其中:φ为内摩擦角;c为岩石黏聚力;E为岩石的弹性模量;ν为岩石泊松比.
考虑充填散体自身重力作用对矿柱提供主动围压作用[21],以及充填散体对矿柱的被动围压作用.因此充填散体对矿柱提供的围压可表示为
(2)
其中:σ3a和σ3p分别为充填散体对矿柱的主动围压和被动围压;γ为散体容重;b为散体装填宽度;H为散体装填高度;φ为散体与矿柱表面的摩擦角;K为侧压系数;Eg为散体变形模量.
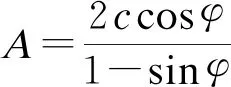
σ1=A+B(C+Egεg).
(3)
将式(1)中εg的表达式代入式(3)整理可得
(4)
σ1与σ3呈线性关系,已知σ1>0和σ3>0,常量A,B,C,E,ν均大于0,变量Eg也大于0,因此式(4)线性规划最优解的可行域在第一象限,如图8所示.可知,矿柱的抗压强度σ1随围压σ3的增长速率取决于方程斜率k,k越大,矿柱强度增长速率越大.假设以k≥n(n>0)为σ1增长速率边界条件,则Eg和E满足式(6).
(5)
(6)
为使式(6)成立,则1-ν-nν>0,因此,式(5)中n满足0 充填散体的刚度是维持系统稳定的关键.充填采矿的本质是充填体置换矿体,假设Eg≥E,此时空区不存在任何失稳问题,但是实际工程中,充填散体刚度不可能大于矿体的刚度,只能向矿体的刚度靠近.因此,Eg和E满足 (7) 图8 σ1和σ3可行域 应用式(7)指导金属矿山干式充填采矿时,Eg越接近E时,矿柱能承载极限压应力越大.Eg受充填散体压实程度的影响,可根据充填散体的压缩试验,得到压缩过程中Eg和其密实度D(密实度为容腔中散体实际体积和散体所占体积之比)的关系,通过控制充入空区充填散体的密实度,更易于指导实际充填采矿. 1) 充填散体对岩柱提供被动侧向支撑作用,使其峰值强度增长了5.06%~19.31%,残余强度保持在至少5 MPa以上. 2) 由于充填散体改善了岩柱受力状态,岩柱的破坏形式由单轴压缩时的伴有侧面劈裂拉伸破坏转化为单斜面剪切破坏. 3) 充填散体约束下,随着岩柱变形增大,充填散体与岩柱的相互作用强度逐渐增大,并且两者之间的这种相互作用随约束散体颗粒粒径增大呈先增后减的变化趋势. 4) 基于试验研究,建立充填散体与矿柱相互作用过程中矿柱的承载模型,得到了散体变形模量与矿柱模量的关系式,为指导金属矿山干式充填开采提供重要理论依据.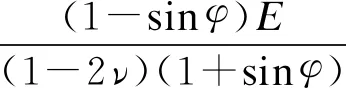

3 结 论
