基于响应曲面法优化振荡天平谐振元件的结构

刘丹丹， 代英鹏， 单 驰， 李德文， 汤春瑞

(1.黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022； 2.中煤科工集团重庆研究院有限公司， 重庆 400037)

0 引 言

目前，在国外振荡天平主要实时监测空气颗粒物、煤矿粉尘、工业废气，以及尾气粉尘浓度和蒸汽沉积等[1]。国内振荡天平法尚应用于大气PM2.5监测中，而振荡天平应用于煤矿粉尘检测时，其谐振元件灵敏度受材料的品质因数、结构形状及质量等因素影响，无法保证浓度检测时的测量准确性。国内学者对振荡天平有诸多研究，李志磊[2]优化复合双管成为整体管型，流通烟尘。李金平等[3]提出利用光散射法辅助提高测量的准确性和有效性。李德文等[4]研究了品质因数对振荡天平测量的重要性。暴翔[5]仿真分析谐振元件不同大小截面，确定振荡特性较高的谐振元件结构。刘丹丹等[6]分析了谐振元件的结构尺寸，优化了微量振荡天平谐振模块，随着煤矿粉尘安全性要求的提高，现有振荡天平的精度已无法满足要求，因此，笔者仿真研究谐振元件的不同结构，利用响应曲面法分析各影响因素对质量灵敏度的影响强度，以保证振荡天平测量装置的精度。

1 振荡天平测量原理

20世纪80年代，振荡天平由美国R&P公司应用于环境颗粒物自动监测领域，其优点为测量原理简单，精度高，可实现连续在线称量[7]。振荡天平法测量原理如图1所示。

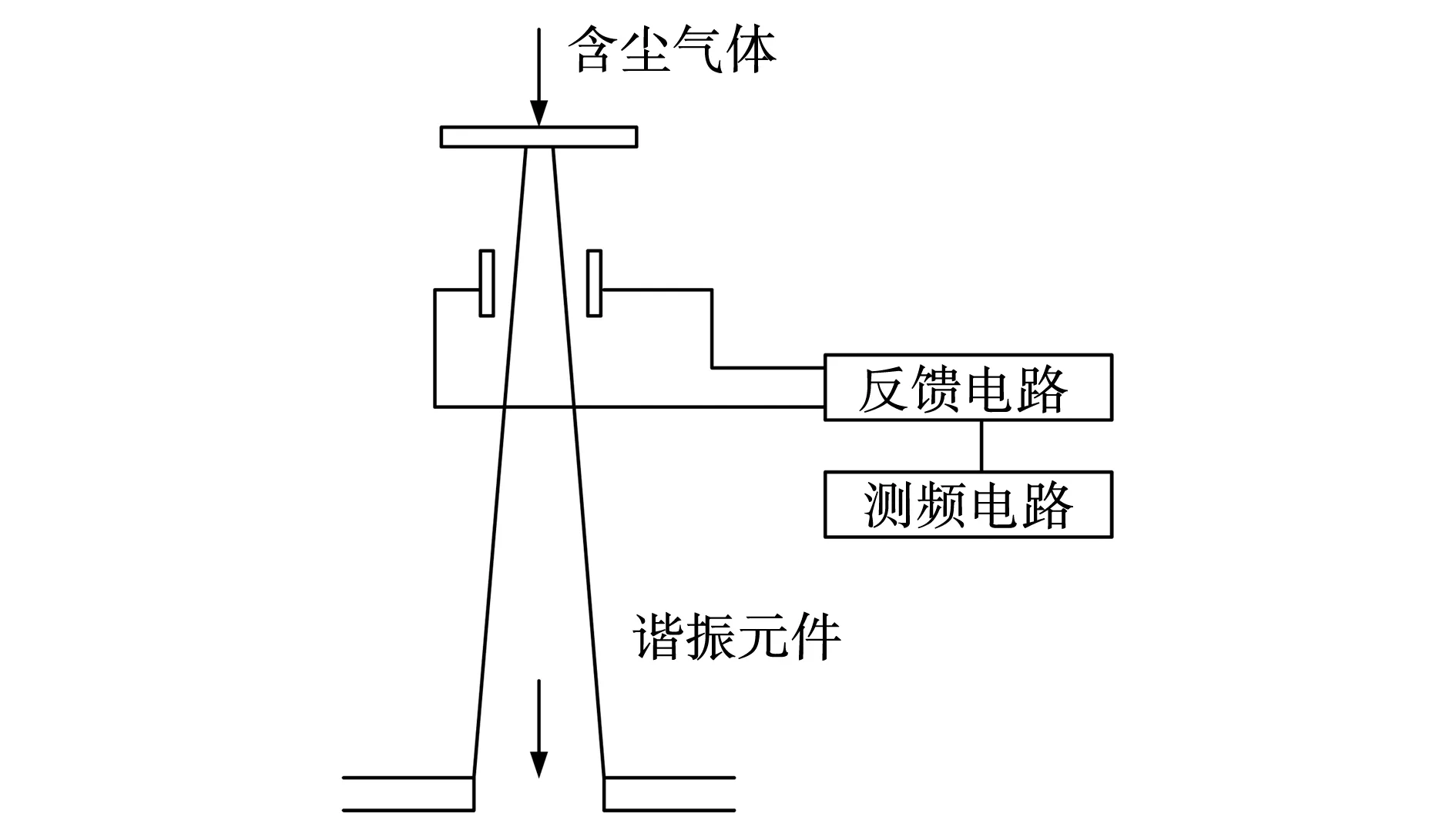
图1 振荡天平测量方法Fig. 1 Measurement method of oscillating balance

振荡天平的核心组件包括谐振元件、检测电路及采样放大电路等，其原理如下：通过使用谐振元件，在装置中将其一端进行固定，另一端实现自由振荡；滤膜设置在自由振荡端的一侧，其作用为能够使含尘气体在通过滤膜时将粉尘颗粒收集起来。利用滤膜和谐振元件能够组成一个较为简便的振荡系统，若测量装置内有含尘气流通过，采样器能够分离特定直径的粉尘，粉尘颗粒将聚集于锥形元件振荡端的滤膜上。当含有粉尘的气体尚未通过时，振荡元件与其两侧的电极板共同组成的电场始终保持特定的频率振荡；若含有粉尘的气体通过后，滤膜质量不断上升，使振荡频率发生相应的变化，利用振荡频率变化能够对滤膜上颗粒物对应的质量进行较为准确的计算，以质量和气体体积之间的比值为依据，计算得出这一时段颗粒物所对应的质量浓度，振荡天平法对应的计算公式为

(1)

ρ=Δm/V，

(2)

式中：Δm——滤膜质量，mg；

k0——恢复力常数,mg/Hz；

f1——空载频率,Hz；

f2——载荷频率,Hz；

ρ——质量浓度,mg/m3；

V——气体体积,m3。

2 谐振元件灵敏度的影响因素

谐振元件称重颗粒物质量时，可以视为变截面悬梁的梁面横向振动，取距谐振元件固定端高度为x，则横向振动的振动方程为

(3)

式中：V(x)——微元段的体积质量,g；

H(x)——微元段的横截面积,m2；

I(x)——微元段横截面抗弯刚度,N/mm；

E——谐振元件材料的弹性模量,Pa；

Y(x)——振动时微元段的横向移动位移,m；

ω——微元段的振动角频率,rad/s。

式(3)中均为x的函数，方程整体为四阶变系数微分方程，难以求解。由式(3)可知，谐振元件的振动频率与其材料弹性模量、体积质量和截面壁厚有关。文中将对国内学者所研究不同形状结构的谐振元件，采用相同材料在Solidworks中建模，导入ANSYS软件中以0.1 mg载荷条件为约束进行模态分析。对文献[3]改进复合双管仿真，得出谐振频率为408.082 Hz，其施加在载荷后的质量灵敏度为0.1 Hz/mg。对文献[6]谐振元件模型进行模态分析，得出谐振频率为790.164 Hz，其质量灵敏度为0.21 Hz/mg；同时，对固定端及振荡端内径分别为4.0和1.5 mm，壁厚为0.5 mm的空心锥形管进行仿真，其质量灵敏度为0.23 Hz/mg对比复合管结构对空心锥形管进行改进，固定端截面的长轴为4.0 mm，短轴为2.0 mm的椭圆结构，其他条件不变进行仿真，四种模型的结构见图2。图中，模型高度H，振荡端内径R，固定端内径短轴长度L。其仿真数据如表1所示。其中，S为颗粒物测量装置灵敏度;μ为频降比，数值越大谐振元件对质量越敏感。

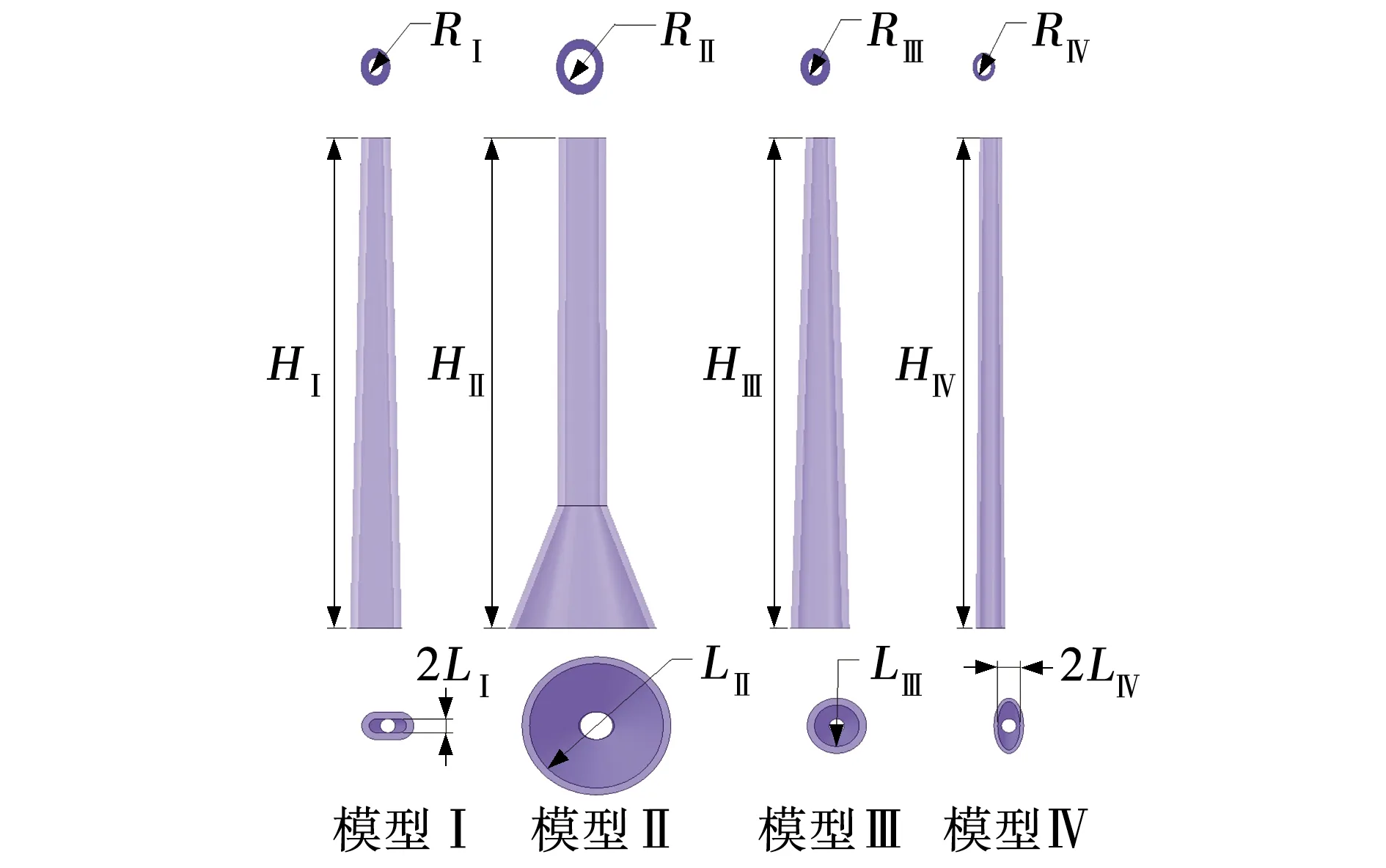
图2 不同模型的结构Fig. 2 Structure of different models

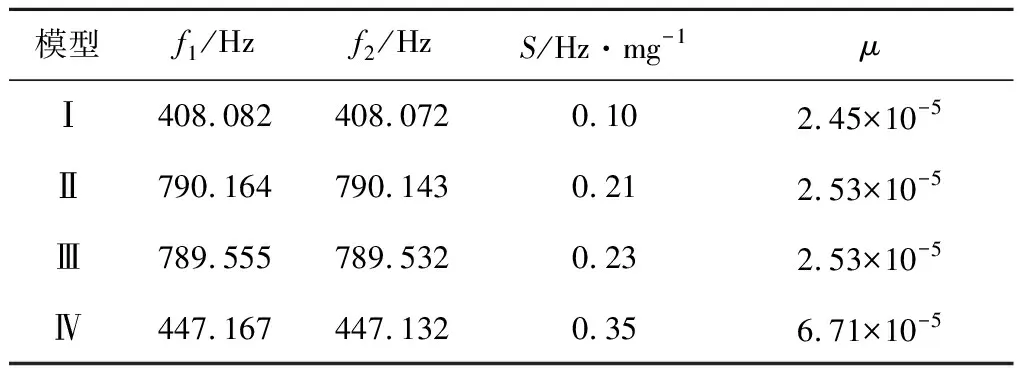
表1 不同模型的仿真数据

由表1可以看出，改进后模型Ⅳ的谐振频率较低，但是其灵敏度及频降比最高，表明此结构对微量颗粒物的分辨率更高，因此，笔者将以其为参考模型，研究高度、固定端内径和振荡端内径对谐振元件灵敏度的影响。

2.1 高度

谐振元件材料相同的情况下，不同高度导致谐振元件的体积质量不同，影响谐振元件的振荡频率，以结构钢制成的参考模型，其他尺寸不变，研究不同高度对质量灵敏度的影响。设置初始高度为100 mm，改变高度对振荡频率进行仿真实验。其实验仿真数据如表2所示。

表2 不同高度的仿真数据

由表2可知，材料相同的情况下不同高度的谐振元件对微量颗粒物的分辨率不同，随着高度增加，谐振元件的灵敏度降低，因此，在设计谐振元件时高度应在80～100 mm之间，从而保证谐振元件对颗粒物有较高的分辨率。

2.2 固定端内径

通过仿真分析固定端截面为椭圆时能够有效抑制二维振荡，以提高振荡频率。在对其内径设计时，为抑制其二维振荡，保持其内径长轴为3.5 mm，改变其短轴长度，初始为1.5 mm，保持其他条件不变进行仿真分析，其仿真数据如表3所示。

表3 固定端内径短轴不同长度仿真数据

由表3可知，当保持圆面、高度不变时，随着椭圆短轴内径尺寸的增加，灵敏度并未发生变化，根据频降比设计椭圆内径短轴长度，获得1.5～1.9 mm之间为最优选择。

2.3 振荡端内径

保持模型其他条件不变的前提下，改变振荡端圆面内径大小，其仿真数据如表4所示。

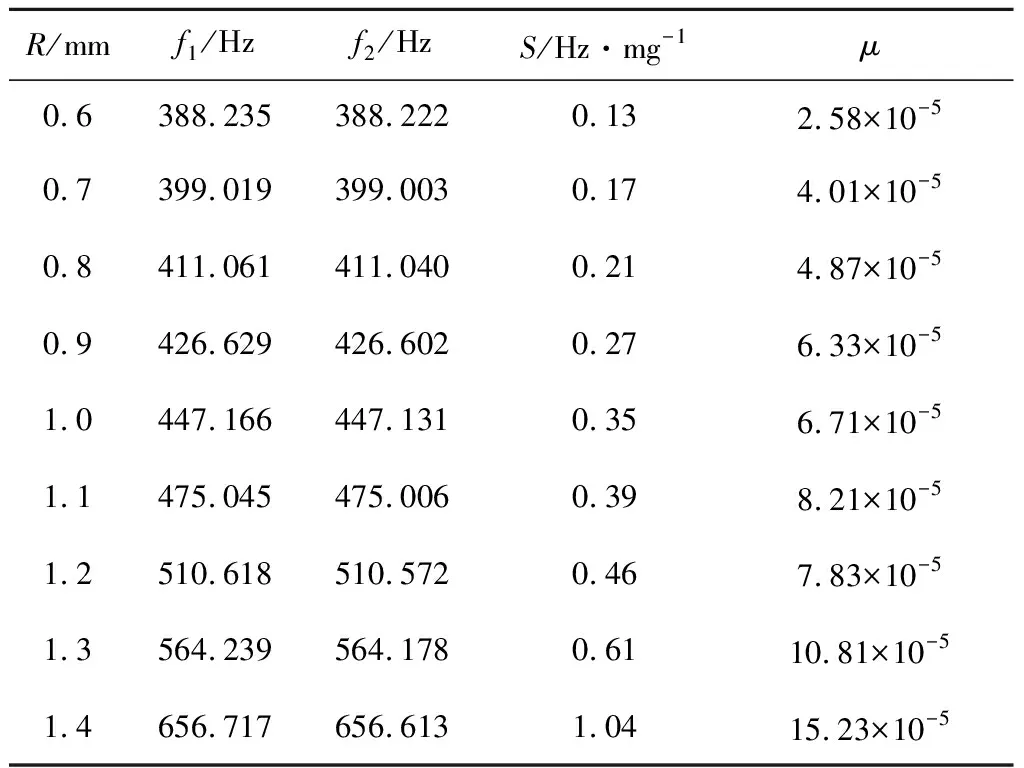
表4 振荡端圆面不同内径仿真数据

由表4可知，若高度保持稳定的情况下，振荡端圆面内径处于1.2～1.4 mm 的范围内，灵敏度及频降比变化较大。

根据上述三种影响因素的仿真结果，高度及振荡端内径对谐振元件的灵敏度影响较大，利用响应曲面法以灵敏度为因变量比较三种因素的影响强度，同时，运用响应曲面法计算获得结构的最优尺寸。

3 响应曲面法的结构优化

响应曲面法是利用数学和统计分析进行参数优化的方法，基本过程是：首先，确定可能含有最佳区域的条件，然后，拟合响应函数与影响因素之间的一阶或二阶模型作为真实响应函数的一个近似，最后，利用一阶或二阶模型得到最优工艺参数[8-10]。

此次研究所使用Box-Behnken设计需要利用的模型数量为13种，并且比完全分析设计所需的33=27种明显较少。无论是拟合一阶、二阶及高阶回归方程，均需要对其回归系数通过最小二乘法完成拟合的过程，并对各种变量进行编码化，为整个过程提供便利[11-14]。

(4)

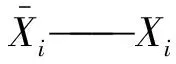
Xih、Xil——第i个变量xi的最大值和最小值,mm。

表5给出了3个实验变量的取值范围。

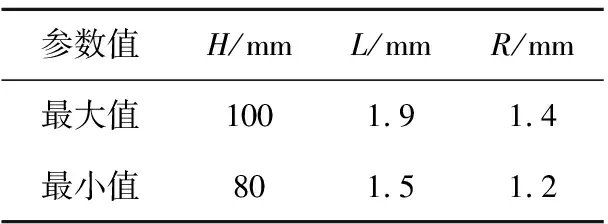
表5 实验参数范围

由响应曲面法的Box-Behnken设计方法，可以得到表6的计算工况，通过ANYSY的有限元分析模块对计算工况进行仿真，得出谐振元件空载与载荷频率，以质量灵敏度为因变量进行最优求解，如表6所示。

表6 计算工况

通过响应曲面法分析，得到不同因素对因变量的响应曲面，从而得出这三个因素各自对灵敏度的影响程度[15-16]，以及三者与灵敏度之间数学模型为

S=-0.325H-0.062 5L+0.437 5r-0.15HR+

0.025LR+0.087 5H2-0.087 5L2+0.212 5R2。

(5)

由式(5)可知，高度与振荡段内径为谐振元件灵敏度的主要因素，各因素对灵敏度的影响如图3所示。

由图3a可知，当椭圆内径短轴长度L不变时，质量灵敏度随着圆面内径r增大而增大；当圆面内径r不变时，椭圆内径短轴长度L对质量灵敏度影响较小，这表明圆面内径对质量灵敏度影响显著。

图3 各因素对灵敏度影响Fig. 3 Effect of various factors on sensitivity

由图3b可知，当圆面内径r不变时，质量灵敏度随着谐振元件高度H增大而减小；当谐振元件高度H不变时，质量灵敏度也随圆面内径r增大，但是影响较高度变化较小。

由图3c可知，谐振元件高度H不变时，质量灵敏度随着椭圆内径短轴长度L变化并不明显；当圆内径短轴长度H不变时，质量灵敏度随谐振元件高度H减小而增大，结果表明，谐振元件高度对质量灵敏度影响最为显著。

通过对影响因素三维曲面的分析可知，测量装置的灵敏度受谐振元件高度和圆面内径影响显著，其最优结构尺寸如表7所示。

表7 最优结构尺寸参数

根据响应曲面优化处理后，得到的谐振元件尺寸为高度80 mm，椭圆面内径短轴为1.68 mm，圆面内径为1.4 mm，在载荷为 0.1 mg时的灵敏度为2.0 Hz/mg，其优化后谐振元件的灵敏度曲线如图4所示。

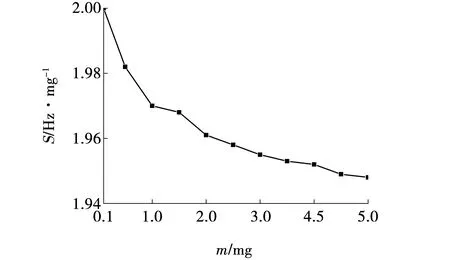
图4 最优结构灵敏度曲线Fig. 4 Optimal structure sensitivity curve

4 结 论

(1)通过有限元仿真分析得出，振荡天平四种不同模型的固定端截面为椭圆，其模型对微量烟尘感应更为灵敏，质量灵敏度为0.3 Hz/mg。

(2)分析和优化了模型Ⅳ的高度、固定端内径椭圆长度和振荡端内径三个影响因素，得出高度为主要影响因素，振荡端内径为次要影响因素，固定端内径对其灵敏度影响最小。谐振元件的最优结构尺寸高度为80 mm，椭圆面内径短轴为1.68 mm，圆面内径为1.4 mm，与优化前的模型Ⅳ相比，质量灵敏度提升了6.6倍。

(3)在最优结构下仿真分析了质量0.1～5.0 mg的载荷，得出最优尺寸下的谐振元件在0.1～5.0 mg载荷内具有较高的灵敏度均在1.94 Hz/mg以上，保证了振荡天平测量装置的精度。