头脑风暴优化算法的SHEPWM逆变器剩余谐波分析

沈显庆， 马志鹏， 孙启智

(1.黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022； 2.哈尔滨理工大学 计算机科学与技术学院， 哈尔滨 150080)

0 引 言

三电平逆变器具有开关器件承受电压低、运行效率高、EMI较少等优点，被广泛应用于中高压大功率场合[1]。但受开关器件损耗限制，其开关频率较低，导致输出电压、电流中低次谐波大量增加。传统调制策略如SPWM[2]、SVPWM[3]，当其工作在高频状态时，输出波形较为理想，但在低频条件下，控制效果较差。而SHEPWM技术在开关频率较低时，可以有选择地消除低次谐波，更好满足大功率系统谐波要求。

SHEPWM技术的难点在于求解一组非线性方程组。传统数值算法，易于实现，但对初值要求较为严格。代数方法，如结式理论[4]、吴方法[5]、Groebner基[6]等，无需初值，但求解复杂，计算效率低。于生宝等[7]将PSO算法用于求解SHEPWM半周期对称方程组，迭代速度快，但对参数选取较为苛刻，易陷入局部最优。贾雨桐[8]提出一种蚁群算法，得到全调制比范围下的一组可行解，求解效果好，但算法搜索时间长，效率较低。郝君等[9]给出神经网络和对称秩相结合的SHEPWM计算方法，解的精度高，但在求解过程中会出现不合理解，降低算法的可靠性。魏远志[10]采用模拟退火算法并对剩余谐波进行分析，求解速度快，全局收敛性强，但仅给出双极性调制方式下的剩余谐波规律，存在着一定的不足。针对上述算法存在的问题，文中提出一种头脑风暴算法优化求解SHEPWM方程组，分析单极性调制方式下的剩余谐波，通过Matlab/Simulink仿真验证该算法的可行性。

1 三电平SHEPWM消谐模型的建立

二极管箝位型三电平逆变器如图1所示。其中，相邻的2个开关器件导通或关断，可以得到不同的输出电压Udc/2、0、-Udc/2。三电平逆变器相电压输出波形如图2所示。

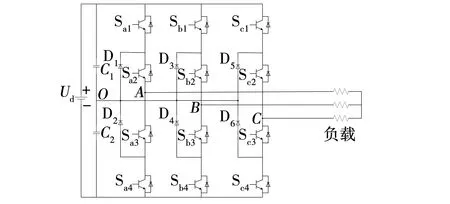
图1 二极管箝位型三电平逆变器拓扑Fig. 1 Three-level NPC inverter topology

图2 三电平逆变器SHEPWM相电压波形Fig. 2 Phase voltage waveform of 3-level inverter

根据Dirichlet定理，图2的相电压波形可由Fourier级数表示：

相电压波形的1/4周期对称，即

An=0，

式中：Umn——n次谐波电压幅值；

N——1/4周期内开关角的数量；

Ud——直流侧电压；

n——谐波次数；

ω——基波角频率；

αi——第i个开关角，i为自然数，依次减小，其值大于0，小于π/2。

由于三相系统之间的对称性，文中仅考虑消除5，7，…，6i-1，6i+1次谐波，得：

(1)

式中：Um1——基波电压幅值；

M——可消除的最大谐波次数；

m——调制比，m=2Um1/Ud。

将式(1)解出，即Umn=0，从而有选择地消除目标谐波。

2 BSO算法的开关角度求解

2.1 BSO算法原理

假设在一个D维的搜索空间内，S={X1,X2,…,XN}代表种群中的N个个体，Xi={xi1,xi2,…,xiD}代表第i个个体的位置。将N个个体利用K-means算法聚合成Q类，将最优适应度的个体作为类中心cq，以概率p1随机选择某个类，并用随机生成的新个体替换cq，在此基础上，以概率p2确定选择一个或两个类用于生成新个体，当选择一个类时，以[0,1]内产生的随机数c11与预设参数c1相比较，决定新个体由cq或随机个体添加“扰动”生成[11-12]。新个体的产生公式为

N(μ,σ)——均值为μ，方差为σ的高斯随机函数；

ξ——步长。

ξ=logsig((0.5T-t)/k)rand()，

式中：T——最大迭代次数；

t——当前迭代次数；

rand()——0到1的随机数；

k——调整logsig()的斜率。

当选择两个类时，产生一个[0,1]之间的随机值c22与预设参数c2相比较，决定新个体由两个类的cq或随机个体融合后添加扰动生成。融合公式为

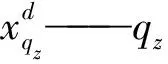
式中：xd——融合后个体的d维分量；

β——0到1之间的随机数；

2.2 BSO算法求解SHEPWM方程组

文中以5个开关角的消谐方程为例，将BSO算法用于方程组求解。将式(1)变换为

cosα1-cosα2+cosα3-cosα4+cosα5-πm/4=δ1，

cos 5α1-cos 5α2+cos 5α3-cos 5α4+cos 5α5=δ2，

cos 7α1-cos 7α2+cos 7α3-cos 7α4+cos 7α5=δ3，

cos 11α1-cos 11α2+cos 11α3-cos 11α4+cos 11α5=δ4，

cos 13α1-cos 13α2+cos 13α3-cos 13α4+cos 13α5=δ5。

定义算法的适应度函数为

0<α1<α2<α3<α4<α5<π/2。

当G取最大值1时，δ1～δ5同时为0，此时，所求出的开关角即为SHEPWM方程组的解。

3 仿真与结果分析

3.1 参数设置

BSO算法参数设置如下：种群规模N=40，聚类数Q=5，替换概率p1=0.2，创造概率p2=0.8，c1=0.4，c2=0.5，最大迭代次数=1 000。计算所得开关角度、相、线电压谐波畸变率(ηTHD)如表1～3所示。

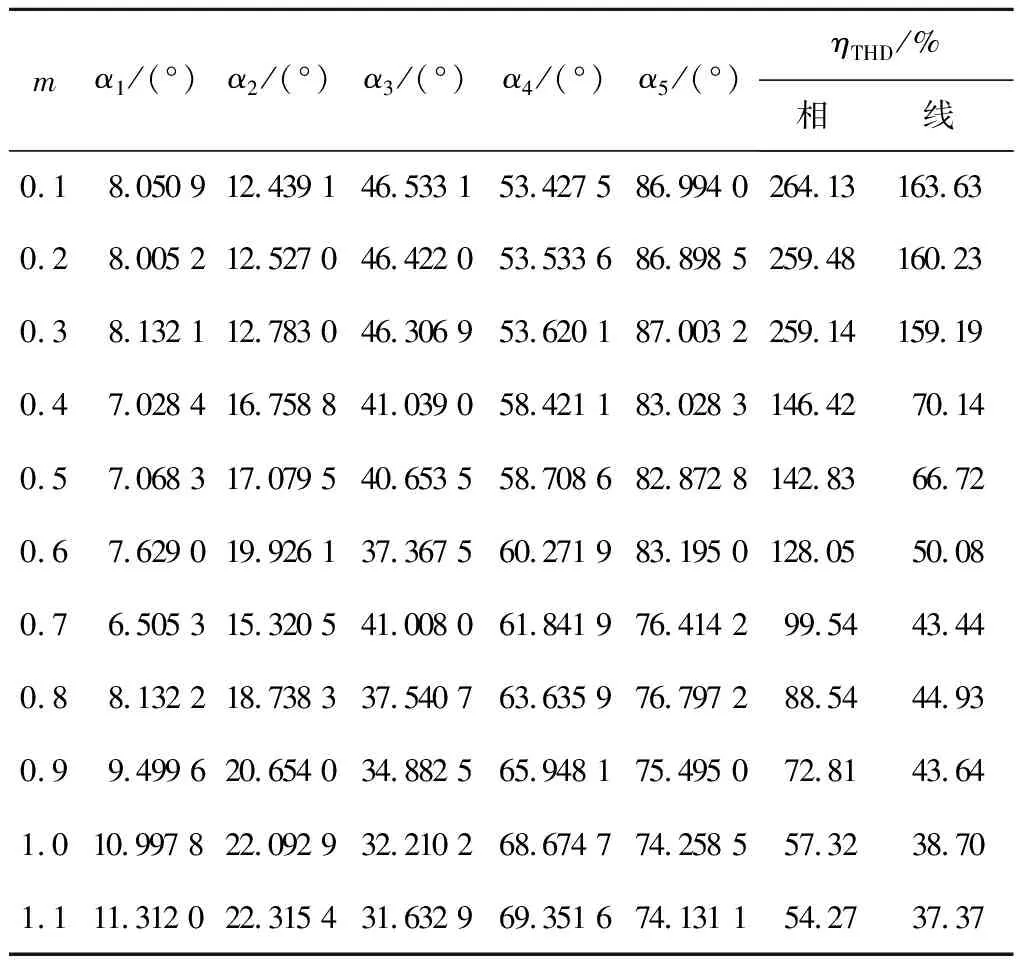
表1 m在0.1～1.1的第1组开关角解集及THD值

表2 m在0.7～1.0的第2组开关角解集及THD值

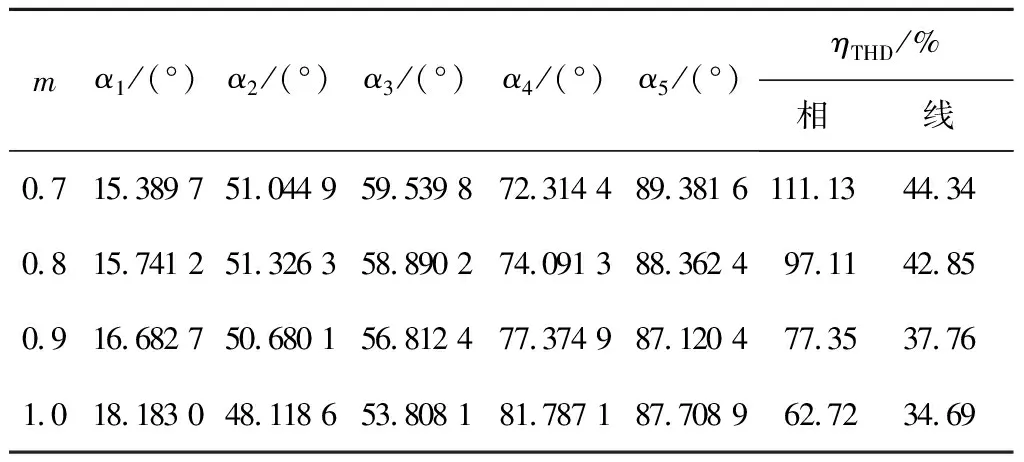
表3 m在0.7～1.0的第3组开关角解集及THD值

由表1～3可见，随着调制比m的增大，相、线电压THD含量逐渐减小，呈单调递减趋势。调制比 在0.1～1.1时的第1组解集其开关角度具有一定的连续性与规律性。调制比m在0.7～1.0时，第2组解的相电压THD值较第1、3组解平均减少约17%和24%，谐波消除更好。因此，在较高调制比m时，对于谐波抑制要求较高的场合，则应尽量选取第2组开关角，更好满足实际消谐要求。理论上在计算第1组开关角时，调制比m在0～1.2的范围内均可解出，调制比m的取值越接近这两个极值时，算法所需的计算时间越长，搜索效率越低，当调制比m取值为0或1.2时，所求出的开关角均不收敛，视为无效解。

3.2 仿真验证

以Matlab/Simulink软件作为建模平台，搭建三电平逆变器[13]，给出m=0.8时的3组不同开关角相、线电压波形及频谱分析，见图3～6。其中，直流电压2 kV，滤波电容3 mF，工频50 Hz。

图3 相电压仿真波形Fig. 3 Phase voltage simulation waveforms

图4 线电压仿真波形Fig. 4 Line voltage simulation waveforms

图5 相电压仿真频谱Fig. 5 Phase voltage simulation spectrum

图6 线电压仿真频谱Fig. 6 Line voltage simulation spectrum

由图3～6的仿真结果可得，相电压中的5、7、11、13次谐波基本消除，线电压中3的倍数次谐波含量为0，证明了该算法的准确性。

4 逆变器剩余谐波分析

特定谐波消除技术通过对逆变器输出电压波形进行Fourier分解，建立N个开关角的非线性方程组[14]，理论上，当N足够大时，SHEPWM可以消除任意次谐波，但受到功率器件开关速度及方程组求解难度的限制，必然会存在剩余高次谐波，其分布规律与开关角个数N和调制比m相关。为验证上述理论分析，以不同开关角数量N、调制比m大小及开关角奇偶性为变量条件，条件1：m=0.5，N=3；条件2：m=0.8，N=3；条件3：m=0.5，N=4；条件4：m=0.8，N=4；条件5：m=0.5，N=5；条件6：m=0.8，N=5进行对比仿真，6种条件下的仿真结果如图7所示。

图7 输出电压剩余谐波分布Fig. 7 Residual harmonic distribution of output voltage

由图7可见，SHEPWM在消除目标谐波后，未被消除的低次谐波幅值增大，输出电压中的总体谐波含量并未缩减，而是向较高次谐波“转移”。如N=3时，11、13、17、19次谐波成为主导谐波；N=4时，13、17、19成为主导谐波；N=5时，17、19、23成为主导谐波。因此，在实际工程应用中，为降低整体谐波能量，可以有针对性的消除最低3～4次谐波，剩余高次谐波含量均小于10%，可以忽略不计。

5 结 论

(1)BSO算法能够得到全调制比范围内的一组开关角解集，与传统数值算法相比，其无需初值，具有计算速度快、搜寻能力强等优点。在此基础上，给出较高调制比下的另外两组解，提高了开关角选择的灵活性，可以达到更好的控制效果。

(2)在单极性调制方式下，目标谐波被消除后，剩余的最低3～4次谐波会成为主导谐波，剩余的高次谐波可以不予考虑。因此，在对谐波要求较为苛刻的场合，可以考虑消除这类谐波，达到减少整体谐波含量的目的。