飞轮微振动的准零刚度多向隔振方法

余 松， 黄可凡， 蒋建平

(中山大学 航空航天学院，广东 深圳 518107)

随着航天技术高速发展，航天工程对于航天器的姿态稳定度和指向精度要求不断提升。在轨航天器上的主要扰动源来自机械转动装置，比如反作用轮和动量轮组。为了降低微振动对航天器高精度载荷的影响，需要对飞轮等扰动源设计隔振装置。

被动隔振装置具有高可靠性和不需要能量输入等优点，适用于太空复杂环境。Pendergast等[1]为Chandra望远镜的飞轮设计了Stewart隔振平台，每根杆单元由3个机械弹簧串并联组成，并利用黏弹性材料提供阻尼，扰动力在13 Hz处开始有效隔振，在100 Hz处的振动衰减能达到近40 dB。Kamesh等[2]设计了由4个正交折臂梁构成的隔振装置，并针对飞轮进行了隔振试验，证明隔振平台能有效降低扰动，然而飞轮转速需要被限制在600～3 500 r/min。Zhou等[3]测试和分析了一种基于折臂梁的被动隔振装置，证明了该隔振平台能有效隔离100～300 Hz的高频扰动，然而在2 600 r/min的时候出现了扰动放大现象。Luo等[4]利用拉格朗日方程建立了飞轮群组和Stewart线性隔振平台的耦合动力学模型，并通过有限元验证了该解析模型的正确性，分析表明飞轮群组的陀螺效应会对耦合系统结构动力学特性产生复杂影响，且隔振系统能有效隔离高频扰动，但低频隔振性能不理想。

由于线性隔振理论不能满足良好的低频隔振效果，非线性隔振理论开始被广泛研究。Tuo等[5]利用谐波平衡法分析了基于准零刚度支杆的Stewart隔振平台在位移激励下的动力学特性和隔振性能。Zhou等[6]利用谐波平衡法分析了基于准零刚度支杆的立方体构型Stewart隔振平台在力激励下的隔振性能。Zhang等[7]采用负刚度技术以实现较低的动态刚度，在一定位移范围内将非线性刚度线性化，通过传递函数矩阵分析了Stewart平台对于飞轮扰动的隔振性能。由于准零刚度隔振器具有高静态刚度、低动态刚度的优势，具有十分良好的低频隔振性能。本文针对飞轮微振动的低频隔振难题，提出基于准零刚度机理的Stewart平台隔振方法，通过理论建模和分析，研究该隔振平台对于飞轮扰动的隔振性能。

1 非线性六自由度隔振平台设计

1.1 隔振平台结构和动力学模型

为解决飞轮微振动的低频隔振难题，采用准零刚度支撑杆设计了六自由度立方体构型的Stewart隔振平台，如图1(a)所示。其中，六根准零刚度杆支撑杆与上下平台通过球铰连接，每两根杆共用一个交点，上平台的圆半径为r，下平台的圆半径为R，上下平台的高度差为H。

图1 Stewart平台示意图Fig.1 Schematic diagram of the Stewart platform

(1)

假设飞轮的中心对称轴与上平台的对称轴zp一致，见图1(a)；上平台为一半径10 cm的匀质薄圆板，m′p为上平台的质量，I′pr和I′pz为上平台的主惯性量，mf为飞轮的质量，Ifr和Ifz为飞轮的主惯性量。飞轮的质心距上平台质心的距离为zc，则飞轮和上平台在坐标系Opxpypzp中的质量和主惯性量为

(2)

定义qp=[qptqpr]T，qpt和qpr为隔振平台的平动和转动自由度，且qpt=[xyz]T，qpr=[θxθyθz]T。定义ω为简谐激励的角频率，f=ω/2π为简谐激励的频率，考虑支杆作用于上平台的合力与合力矩以及简谐激励，基于准零刚度支杆的Stewart隔振平台的动力学方程为

(3)

其中，

(4)

1.2 增量谐波平衡法求解

令τ=ωt，则式(3)可重写为

(5)

设qp0和ω0为式(5)的解，则其邻近状态可用增量形式表示为

qp=qp0+Δqp,ω=ω0+Δω

(6)

将式(6)代入式(5)可得

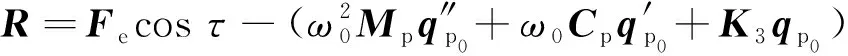
(7)

假设响应具有一阶和三阶谐波项，则上平台的位移响应qp0和增量Δqp可表示为[9]

qp0=SA, Δqp=SΔA

(8)

其中，

S=diag(CS,CS,CS,CS,CS,CS),
A=[A1A2A3A4A5A6]T,
ΔA=[ΔA1ΔA2ΔA3ΔA4ΔA5ΔA6]T,
CS=[cosτcos 3τsinτsin 3τ],
Aj=[aj1aj3bj1bj3]T,
ΔAj=[Δaj1Δaj3Δbj1Δbj3]T

将式(8)代入式(7)并运用伽辽金平均过程可得

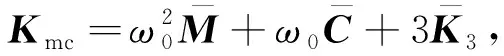
(9)

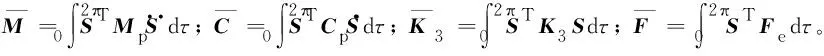
1.3 参数分析

下面通过增量谐波平衡法分析隔振系统参数及微小幅值的多向简谐激励对隔振系统运动响应以及隔振性能的影响。表1给出了设计的隔振系统参数，其中飞轮的参数来源于工程部门的实际型号；准零刚度支杆选择两种刚度系数k3(Ⅰ)和k3(Ⅱ)。

表1 隔振系统参数Tab.1 Parameters of the isolation system

飞轮转动产生的径向扰动力和扰动力矩主要是由于转子质量的静动不平衡造成的，表现为飞轮转速下的基频[10]。而轴向扰动由轴承的非线性振动引起，以倍频形式的高频扰动出现[11]。下面忽略轴向扰动，考虑径向扰动下的三种微小简谐激励的幅值：①Fx=Fy=0.004 N，Mx=My=0.000 5 N·m，Fz=Mz=0，对应下文中飞轮300 r/min时的扰动幅值；②Fx=Fy=0.06 N，Mx=My=0.008 N·m，Fz=Mz=0，对应下文中飞轮1 200 r/min时的扰动幅值；③Fx=Fy=1 N，Mx=My=0.14 N·m，Fz=Mz=0，对应下文中飞轮5 000 r/min时的扰动幅值。为了验证增量谐波平衡法求解系统稳态响应的准确性，将所求的近似解析解与数值解进行对比。图2和图3分别是在激励情况②下，对于准零刚度系数Ⅱ，当简谐激励频率为2 Hz时，上平台x方向角位移和y方向位移的运动响应曲线和幅值频谱图。由图2可知，IHB解与数值解吻合较好。由图3可知，由于系统中只存在三次非线性项，稳态响应中只含奇数阶谐波分量，同时通过增量谐波平衡法得出的一阶、三阶谐波分量的幅值与快速傅里叶变换的结果较为吻合。

图2 激励情况②下隔振平台的运动响应(类型Ⅱ)Fig.2 Response of the vibration isolation platform under circumstance ② (type Ⅱ)

图3 激励情况②下隔振平台的幅值频谱图(类型Ⅱ)Fig.3 Spectrum for the vibration isolation platform under circumstance ② (type Ⅱ)

上平台通过支腿的扰动输出为

(10)

采用功率传递率评价非线性隔振系统的隔振性能，其定义为扰动输出力(力矩)和激励力(力矩)在一个周期内平均功率的比值[12]。

应用增量谐波平衡法求解式(3)，图4和图5分别比较了激励情况②下，不同准零刚度系数隔振平台的一阶谐波响应的幅频曲线和功率传递率曲线，其中实线为类型Ⅰ，虚线为类型Ⅱ。由图4可知，由于刚度耦合效应，z方向的平动和转动自由度也会振动，但其振动幅值远小于x和y方向自由度的振动幅值。由于立方体构型Stewart平台的结构不对称性，x和y方向自由度的振动幅值并不完全相同。增加准零刚度系数k3，x和y方向的平动位移和转动位移的幅值在低频部分会减小。

图4 激励情况②下不同k3的隔振平台一阶谐波的幅频曲线Fig.4 FRCs of the first-order harmonic of the platform for different k3 under circumstance ②

由图5可知，对于类型Ⅰ的准零刚度支杆，低频部分的传递率共振峰几乎消失，具有非常好的低频隔振效果。增加准零刚度系数(类型Ⅱ)，会使低频部分出现明显的共振峰，显著降低在低频段的隔振性能，但是还未发生跳跃现象。两种类型的准零刚度支杆产生一致的高频隔振性能。

图5 激励情况②下不同k3的功率传递率Fig.5 Power transmissibility for different k3 under circumstance ②

图6比较了刚度类型Ⅰ下，三种激励情况的径向力和力矩的功率传递率。点画线、虚线和实线分别对应激励情况①②③。由图6可以发现，当激励幅值很小时(情况①和情况②)，激励幅值对功率传递率几乎没有影响，且低频部分几乎没有出现共振峰。当激励幅值增大到一定程度后(情况③)，功率传递率在低频部分出现了共振峰，这是由于低频部分的位移幅值增加，超出了低刚度区域，从而削弱了低频隔振性能。但是，增大激励幅值对高频部分的功率传递率几乎没有影响。对于高频隔振，在100 Hz处，扰动力和力矩输出能降低90%。

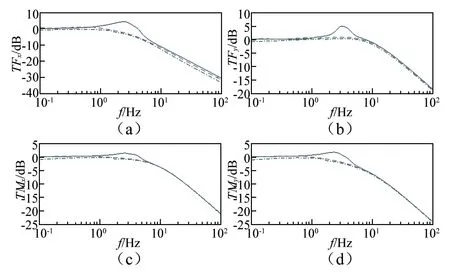
图6 不同激励幅值下的功率传递率(类型Ⅰ)Fig.6 Power transmissibility for different excitation amplitude (type Ⅰ)

通过分析发现，表1所给的参数对于微小幅值的多向简谐激励具有十分良好的低频隔振性能。

2 飞轮与隔振平台的耦合动力学建模

图7(a)是飞轮与隔振平台安装的三维示意图，飞轮放置在上平台的正中央，转子的中心对称轴与上平台的对称轴zp一致。

建立如图7(b)所示的坐标系，定义如下：

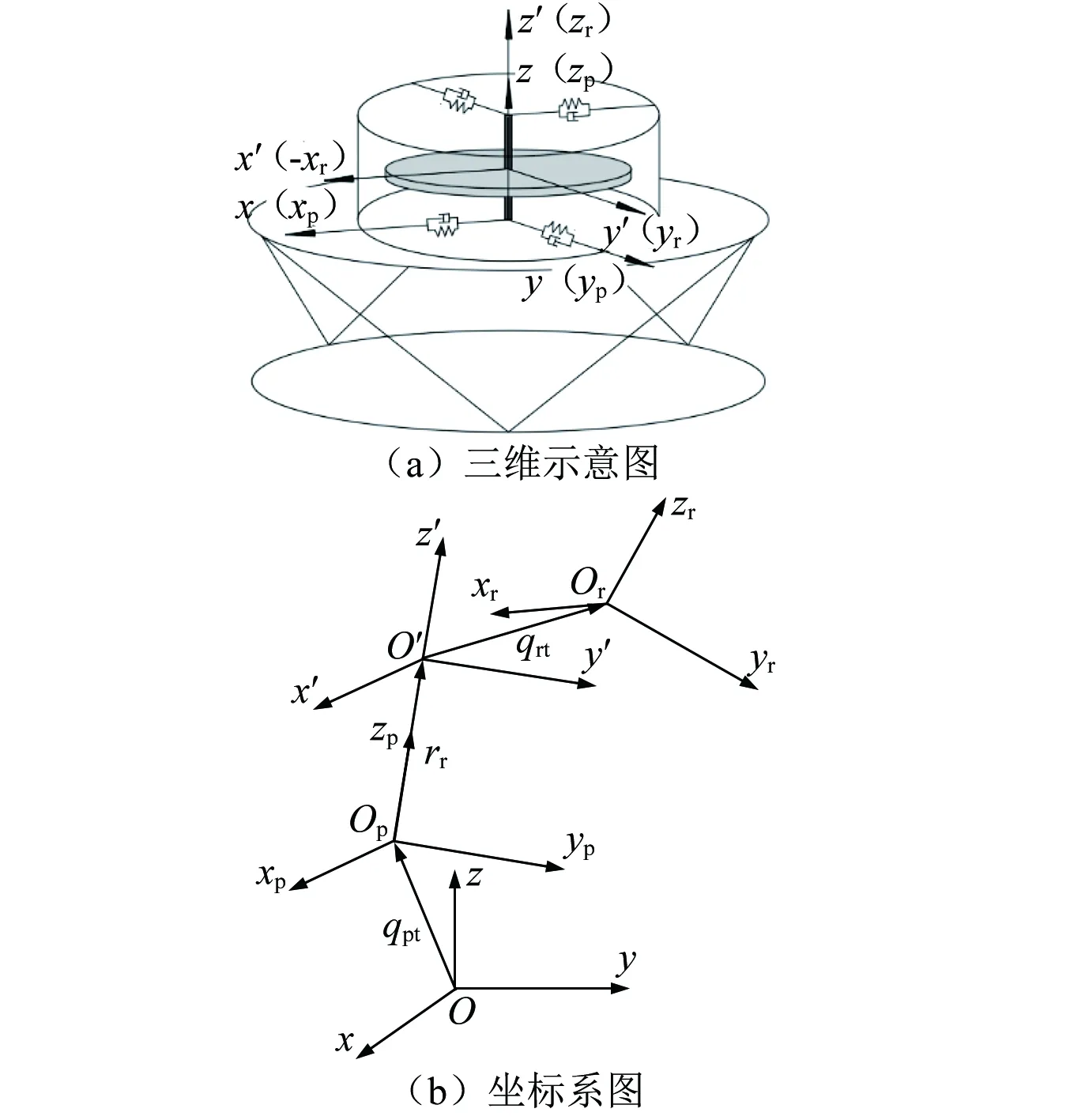
图7 飞轮与隔振平台示意图Fig.7 Schematic diagram of the Stewart platform and flywheel

(1) 隔振平台惯性坐标系oxyz；

(2) 隔振平台连体坐标系opxpypzp——原点位于隔振平台的质心，ox，oy，oz轴对应平台的惯量主轴。初始时刻隔振平台连体坐标系和隔振平台惯性坐标系重合；

(3) 转子惯性坐标系o′x′y′z′——随隔振平台连体坐标系一起平移和转动；

根据图4所示的不同围压下的应力应变关系曲线，可以得到不同砂粒含量下的砂质黄土的摩尔-库仑抗剪强度包线如图5所示。由不同砂粒含量下砂质黄土的摩尔-库仑抗剪强度包线可以得到其抗剪强度强度参数如表2所示。

(4) 转子连体坐标系orxryrzr——原点位于转子的质心，ox，oy，oz轴对应转子的惯量主轴。初始时刻转子连体坐标系与转子惯性坐标系重合。

令qr=[qrtqrr]T，qrt=[uv]T，qrr=[φψ]T，u和v代表转子相对于转子惯性坐标系o′x′y′z′的平动自由度，φ和ψ代表转子相对于转子惯性坐标系o′x′y′z′的转动自由度。rr为上平台质心到初始时刻转子质心的矢径，设rr=[0 0h]T,h为转子到隔振平台的安装高度。令mr为转子的质量，Irr和Irz为转子的主惯性量，cu和cφ分别为轴承的径向阻尼和摇摆阻尼，ku和kφ分别为轴承的径向刚度和摇摆刚度，Us和Ud分别为转子的静不平衡量和动不平衡量，Ω为转子的角速度。在隔振平台惯性坐标系中，转子的四自由度动力学模型为

(11)

其中，

(12)

qra代表转子在隔振平台惯性坐标系中的绝对平动位移和绝对欧拉角。由图5(b)可知

qrta|3×1=qpt+rr+qrt|3×1

(13)

对式(13)求二阶导可得

(14)

(15)

由于初始时刻，4个坐标系各轴均对应平行，故

qrra|3×1=qpr+qrr|3×1

(16)

考虑式(15)和式(16)，则式(11)可改写为

mr0mr2×3-mrr～r2×30Ir0Ir2×3q··rtq··rrq··ptq··pr+Cu0000Cϕ+G0G2×3q·rtq·rrq·ptq·pr+Ku00Kϕ0qrtqrrqptqpr=FuTu

(17)

式中，Π|m×n(m≠n)为将矩阵或向量Π缩减或扩展为m行n列，扩展部分以0补充。

在隔振平台惯性坐标系中，隔振平台的动力学模型为

(18)

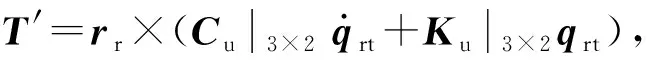
(19)

结合式(15)和式(19)，式(18)可改写为

00mp0mrr～r3×20mrr～rIp+mrr～rr～Trq··rtq··rrq··ptq··pr+-Cu3×200-Cϕ3×2Cpq·rtq·rrq·ptq·pr+

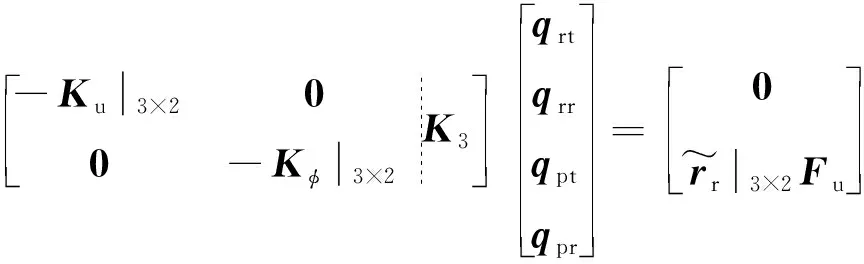
-Ku3×200-Kϕ3×2K3qrtqrrqptqpr=0r～r3×2Fu

(20)

式中：mp=diag(mp,mp,mp)；Ip=diag(Ipr,Ipr,Ipz)。值得注意的是，此时的mp，Ipr和Ipz为上平台、飞轮定子及外壳附属件在坐标系opxpypzp中的质量和主惯性量。

结合式(17)和式(20)，飞轮隔振平台耦合动力学模型可写为

(21)

其中，

(22)

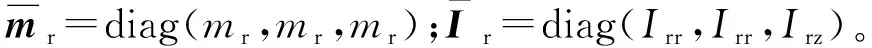
根据耦合动力学模型式(21)可知，飞轮转子的质量、主惯性量和陀螺项与隔振平台发生了耦合。当不考虑耦合时，假设飞轮与上平台为一个整体，并在转子的质心处施加随转速变化的扰动力和力矩，该扰动力和力矩根据转子的四自由度动力学模型得出，并记此模型为简化模型。

3 飞轮隔振分析

表2给出了飞轮转子的参数，其中转子的质量和惯量来源于工程部门的实际型号参数；转子的轴承刚度及静动不平衡量是结合工程部门的飞轮扰动测试数据，根据飞轮的扰动模型，参考罗青研究中表5.1得到的。由于轴承的阻尼很小，可近似为零。

表2 转子参数Tab.2 Parameters of the rotor

3.1 隔振性能分析

根据表1和表2的参数，用龙格库塔法求解式(21)，可得隔振装置的扰动输出如图8所示，其中虚线为隔振前飞轮输出的扰动力和扰动力矩的幅值，实线和点画线分别为对耦合模型和简化模型隔振后，上平台通过支腿输出的扰动力和扰动力矩的最大值，类型Ⅰ和类型Ⅱ的曲线几乎完全重合，且耦合模型和简化模型的结果差别不大。由于y方向和x方向一致，为简便起见，这里只给出了x方向的扰动输出。由图8可以看出：①隔振装置具有良好的低频隔振效果，且不存在共振放大现象，可以实现飞轮径向扰动力和扰动力矩的全转速隔振；②在转速1 000 r/min处，扰动力输出降低了31.26%，扰动力矩输出降低了46.16%；③在转速3 000 r/min处，扰动力输出降低了73.41%，扰动力矩输出降低了83.23%；④在转速6 000 r/min处，扰动力输出降低了91.03%，扰动力矩输出降低了94.10%。⑤在一定阻尼大小下，准零刚度系数对飞轮微振动隔振性能的影响不大，这是因为飞轮转子输出扰动力和力矩的大小与其转速有关。根据图5，情况②的简谐激励幅值对应飞轮1 200 r/min时的扰动幅值，飞轮1 200 r/min时输出的扰动为频率20 Hz的简谐激励。在图5中，两种准零刚度系数在频率20 Hz的简谐激励下对应的功率传递率一致，所以其对飞轮1 200 r/min时的隔振效果并无影响。

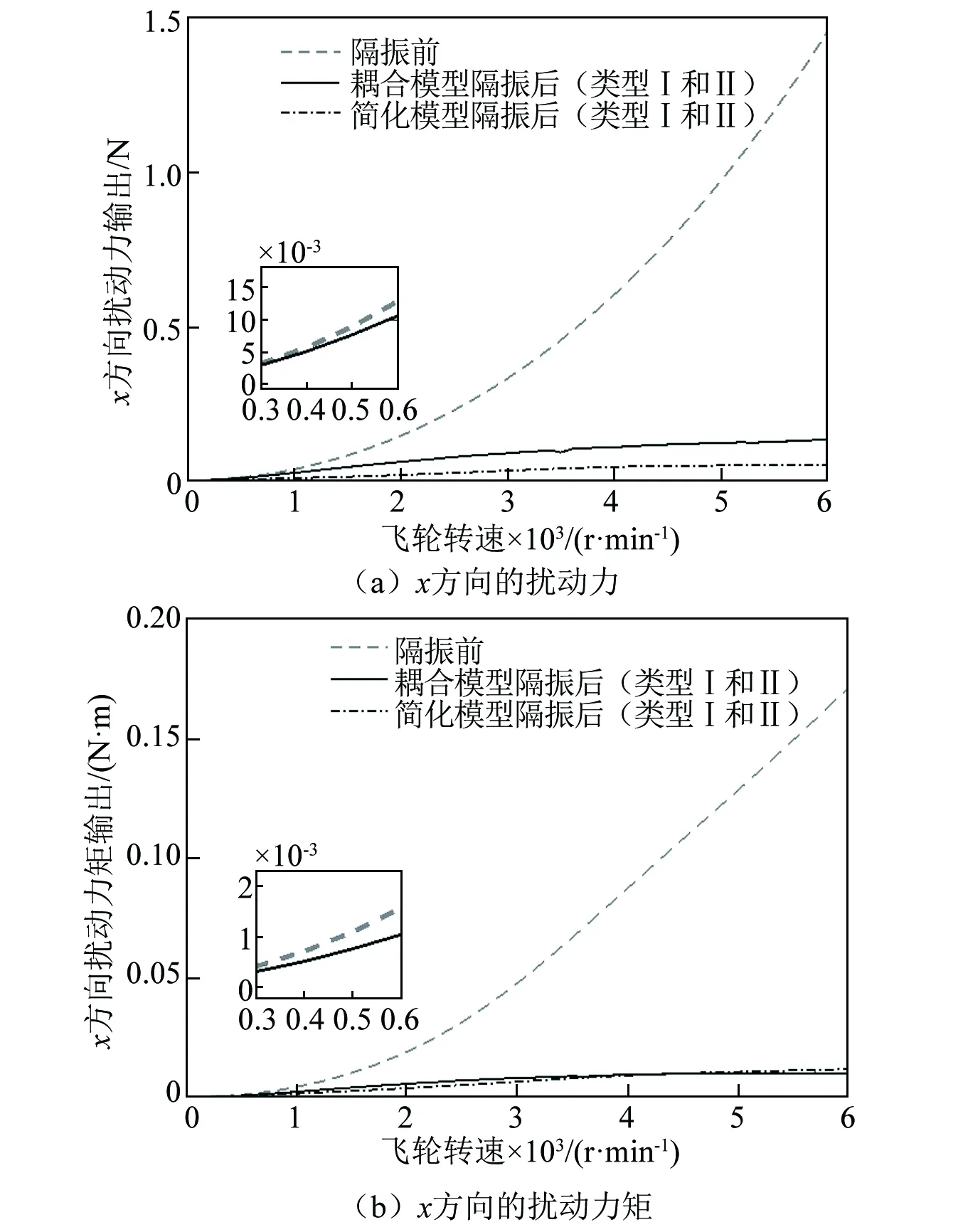
图8 隔振前后飞轮的扰动输出Fig.8 The output disturbance of flywheel before and after isolation

3.2 隔振平台角位移响应分析

航天任务中对飞轮系统动量矩矢量的指向精度控制在6×10-4rad(≈0.033°)以内。由于多自由度线性隔振平台的共振频率是固定的，在发生共振处最有可能使径向角位移不能满足精度要求，因此需要增加支腿刚度，从而削弱了低频隔振效果。而准零刚度隔振平台发生共振的频率和激励幅值有关，对于较小飞轮转速的激励幅值，不会出现共振；对于较大飞轮转速的激励幅值，即便出现了共振，但共振频率远低于飞轮转速下的基频，因此不会放大飞轮的角位移。

图9对比分析了耦合模型和简化模型下，隔振平台最大径向角位移随转速变化的规律。由图9可见，简化模型的结果与耦合模型的结果有一定的差别。在一定阻尼大小下，准零刚度系数对最大径向角位移的影响很小，同时径向角位移满足指向精度要求。

图9 隔振平台的最大径向角位移Fig.9 The maximum radial angular displacement of the platform

4 结 论

本文研究了基于准零刚度机理的飞轮微振动非线性隔振方法。通过准零刚度支杆搭建立方体构型的Stewart隔振平台，分析了在微小振幅的简谐外激励下，激励幅值和准零刚度系数对隔振性能的影响。然后在四自由度飞轮线性扰动模型的基础上，建立了飞轮和隔振平台的耦合动力学模型。结果表明，基于准零刚度支杆的Stewart隔振平台能消除飞轮的扰动放大现象，提高低频隔振性能，实现飞轮的全转速隔振，并且径向角位移响应幅值能满足飞轮动量矩矢量的指向精度要求。