基于Poincare截面突变特性的管道小缺陷识别与评估
2022-02-16成梦菲张伟伟闫晓鹏马宏伟
成梦菲, 张伟伟, 王 晶, 闫晓鹏, 马宏伟
(1. 太原理工大学 机械与运载工程学院,太原 030024; 2.太原科技大学 力学系,太原 030024;3.东莞理工学院 建筑工程系,广东 东莞 523808)
管道作为能源运输的主要工具之一,由于服役时间长,工作环境恶劣等原因,在其服役过程中不可避免的会出现裂纹、腐蚀等缺陷,在管道出现小缺陷的早期及时发现并进行修复可以有效的保障管道服役的安全。超声导波检测技术作为一种长距离检测方法,自提出后便在管道缺陷检测中显示出了显著的优势[1-4]。然而,由于检测信号受到缺陷大小和传播距离的影响,对于小缺陷检测,测试信号往往表现为强噪声下的弱导波信号特征[5]。为了提高小缺陷的检测灵敏度,研究人员从超声导波的传播特性[6]、检测装置[7]、信号处理等方面对超声导波检测技术进行了优化,而现有的信号处理方法在处理含强噪声的弱导波信号时均有一定的局限性,如短时傅里叶变换[8]无法兼顾时间分辨率与频率分辨率,对长周期的导波信号可能会漏检;小波变换[9]要确定合适的分解层数以及小波基函数比较困难;时间反转聚焦法[10]需要预判缺陷大致位置以确定时反窗的起点及宽度,在实际工程应用中往往难以实现;滤波法[11]的中心频率并不稳定,加之导波具有旁瓣,增加了滤波的难度。
混沌系统具有较强的参数敏感性与噪声免疫能力,利用这一特点可以直接将信号以扰动项的方式输入到系统中,从系统响应中识别弱信号,而不需要再对信号进行分解、重构、降噪等处理,显著降低了信噪比门限,提高了检测灵敏度,相较于现有方法具有明显优势。混沌系统的这一特征为提高弱信号检测灵敏度提供了有效的途径,研究人员围绕弱信号检测的理论和实践问题展开了深入的研究。不过,基于混沌系统敏感性的弱信号检测技术多用于检测简单的正、余弦信号[12-14],而对于超声导波信号的检测研究相对较少。张淑清等[15]以时域图为指标,对Duffing系统检测导波信号的相位和幅值进行了数值研究,指出了Duffing系统在超声导波检测中的潜力,但其缺乏一定的实例验证。邹珺等[16]则进一步以相轨图为混沌指标,实现了对钢绞线试验导波信号的检测,将混沌系统的检测范围推广到了超声导波领域,但其仅通过试验验证了利用混沌系统敏感性检测超声导波信号的可行性,缺乏对检测系统参数设定方法的探讨。张伟伟等[17-20]以(-x3+x5)替代(-x+x3),利用改进型Duffing系统开展以相轨图、Lyapunov指数为指标的超声导波检测方法研究,实现了缺陷识别与定位,不过,由于Lyapunov指数计算复杂,计算量大,不利于缺陷的快速识别且无法评估缺陷大小。本文以Poincare截面刻画Duffing系统的状态,将系统由周期态向混沌态转变的临界态作为弱导波信号的检测系统,发展了一种快速的超声导波识别方法。该方法首先计算Duffing系统的分岔图,结合Poincare截面确定检测系统参数;然后,将超声导波测试信号叠加到检测系统的外驱动力项中,通过观察系统Poincare截面是否发生突变来判断测试信号中是否含有导波信号;最后,在Poincare截面上构造胞空间,计算Poincare截面上的点占据胞元数,并将其定义为损伤指标,给出了管道缺陷大小评估方法。
1 Poincare截面与弱导波信号检测
1.1 基于Poincare截面的检测原理
Duffing方程是一类典型的非线性系统,它具有周期、混沌、分岔等混沌系统的典型特征,其表达式为
(1)
式中:k为阻尼系数;-x+x3为非线性恢复力;F为驱动力幅值;ω为驱动力角频率。管道超声导波检测中,经Hanning窗调制的单音频正弦信号应用广泛,导波信号的表达式为
(2)
式中:A为信号幅值;n为单音频数目;ω=2πfc,fc为中心频率。将式(2)所示导波作为外驱动力的扰动项叠加在式(1)的右边,则导波信号检测系统可写为
(3)
(4)
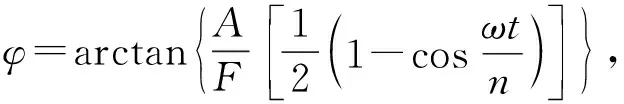
Poincare截面是识别非线性系统状态的一个有效指标,其原理简单、计算量小,兼具了定性与定量判定的优点。对于N维自治系统,可在N维相空间中选取适当截面,该截面上对某一对共扼变量取为固定值,借助计算机将相空间的连续轨迹与该截面的交点显示出来,该截面即为Poincare截面。对于非自治系统,以驱动力周期为采样周期对系统输出进行等周期频闪采样,可获得Poincare截面[21]。若不考虑系统初始阶段的暂态过程,只考虑稳态解,利用Poincare截面,可以形象直观的判断系统状态:①当Poincare截面上只有一个不动点或少数离散点时,运动是周期的;②当Poincare截面上是一封闭曲线时,运动是拟周期的;③当Poincare截面上是一些成片的密集点且有一定层次结构时,运动是混沌的。
1.2 检测系统参数选取
在管道超声导波检测中,中心频率为70 kHz的L(0.2)模态导波常被用来检测环向裂纹,这里,我们将以此作为待检信号。根据Wang等的研究,只有外界输入信号频率等于检测系统频率时,系统状态才会敏感的依赖于输入信号,为此,设置系统驱动力圆频率ω为
ω=2π×70 000≈439 823 rad/s=0.439 823 rad/μs
当频率ω一定时,激励幅值与阻尼系数满足F/k>c时,系统可能出现混沌状态,其中c为一常数[22]。为了减小计算量,在小范围内寻找系统关于F的混沌阈值,k的取值不宜过大,此处取k=0.4。在确定了频率ω和阻尼k之后,为了获得使检测系统处于临界状态的F,先考虑式(3)中A=0,即不输入任何信号(与式(1)等价)时,讨论系统随F的分岔图,具体计算为:①设定F的取值范围为F(0,1),增量为5×10-5;②以位移为分岔指标,对式(1)采用四阶龙格-库塔方法求解,时间步长设为0.02 μs,初值设为(0,0),计算时长为800个外激励周期,绘制出分岔图。
由于本文选取的Duffing方程并没有被赋予实际的物理意义,因此利用该方程的参数做出的分岔图,Poincare截面图中的坐标轴参数均无单位。系统随驱动力幅值变化时的位移分岔图,如图1所示。其中,F=0.556 55为系统由周期向混沌过渡时的混沌阈值,此时所对应的Poincare截面如图2(a)所示,可见该状态下Poincare截面上只有一个点,表明系统处于周期态;而当F减少一点,F=0.556 50时,画出系统Poincare截面图,如图2(b)所示,Poincare截面呈现为沿着一条弧线分布的密集点集,并表现出一定层次结构,表明系统进入了混沌状态。因此,将ω=0.439 823,k=0.4,F=0.556 55的Duffing方程设定为检测系统,当导波信号输入后,即便驱动力有微弱的改变也会导致系统的显著变化,系统将由周期态变为混沌态,从而Poincare截面也由一个点突变为密集点集,利用这一特性可以实现对弱导波信号的识别。

图1 系统关于激励幅值F的分岔图Fig.1 Bifurcation diagram of the system depending on excitation amplitude F
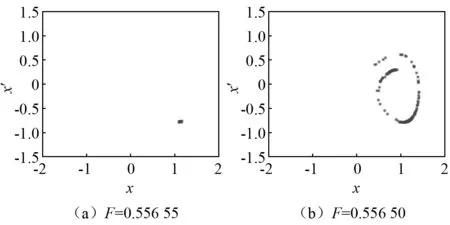
图2 不同激励幅值下系统的Poincare截面Fig.2 Poincare section of the system with different excitation amplitudes
1.3 Poincare截面的噪声影响分析
由于在检测时会不可避免的受到噪声影响,为了验证Poincare截面的噪声免疫能力,在计算机中生成式(2)所示的导波信号,令A=0.000 5,ω=0.439 823,n=10,则导波信号如图3(a)所示,考虑如下高斯白噪声模型
(5)
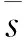
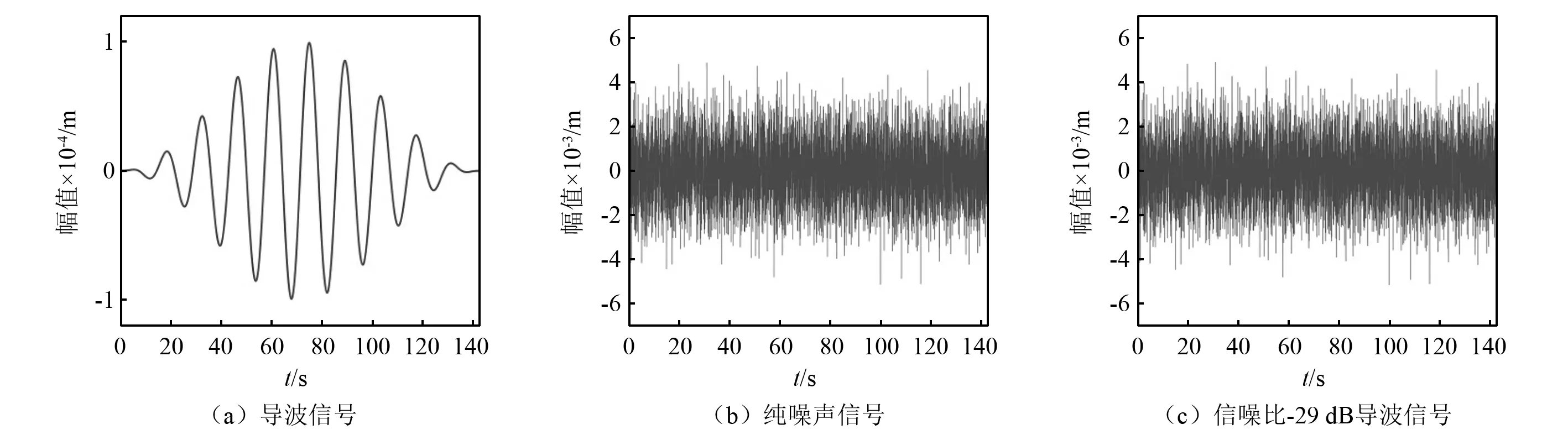
图3 待测信号Fig.3 Signal to be tested
将图3所示的纯导波信号、纯噪声信号,以及受噪声污染的导波信号输入到检测系统中,其结果如图4(a)~图4(c)所示。当导波信号输入后,Poincare截面表现为成片的密集点集且沿一条弧线分布,表示系统进入混沌状态,如图4(a)所示,这是由于导波信号频率与Duffing系统驱动力频率相同,输入导波信号后相当于改变了驱动力幅值,由Duffing系统的参数敏感性,即便是幅值很小的导波信号也会引起系统的混沌相变;图4(b)为纯噪声信号检测结果,Poincare截面仅有一个点,表明系统处于周期态,这验证了Poincare截面对噪声的抗干扰性;最后,将信噪比为-29 dB的含噪声导波信号输入到检测系统中,其识别结果如图4(c)所示,系统处于混沌状态,说明导波信号被检测到,这也验证了Poincare截面对强噪声下弱导波信号的检测能力。

图4 检测结果Fig.4 Detection result
2 试验研究
2.1 试验装置
为了验证所提方法的有效性,本文选取一段5 m长的无缝钢管进行试验参数研究,其外径为88 mm,厚4 mm,利用一对半圆形支座将管道悬空架起,管道两端自由。试验照片和试验原理,如图5所示。采用PZT5材料作为传感器,按照管道断面尺寸加工压电环,厚度为2.5 mm(厚度方向谐振),利用AB胶粘贴在管道一端,产生对称的L(0,2)模态导波。接收端利用一组16片均布管道一周的压电片并联作为接收传感器,每片压电片在长度方向谐振,尺寸为15 mm×2.5 mm×0.8 mm。试验设备主要包括任意信号发生器、低频功率放大器和示波器如图5(a)所示。测试信号中心频率为70 kHz,采样频率为2.5 MHz。
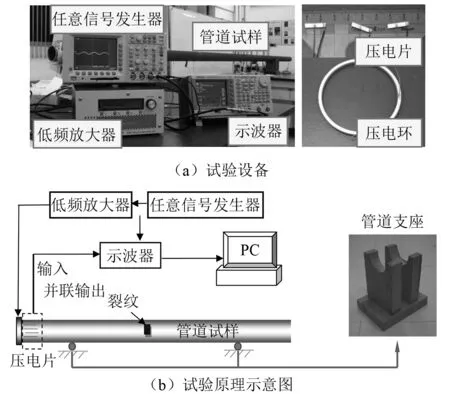
图5 试验装置及试验原理图Fig.5 Experimental device and principle
利用锯弓在距离信号激励端3 m处加工缺陷。第一种通槽,选择1/8圆弧,如图6(a)所示,深度分别为1 mm,2 mm;第二种缺陷选择3/16圆弧,缺陷边缘和圆弧相切,深度为2 mm,如图6(b)所示;第三种选择1/4圆弧,缺陷边缘和圆弧相切,缺陷中心距管道表面距离表示裂纹深度,加工2 mm, 2.5 mm两种深度裂纹,如图6(c)所示。所有工况如表1所示。
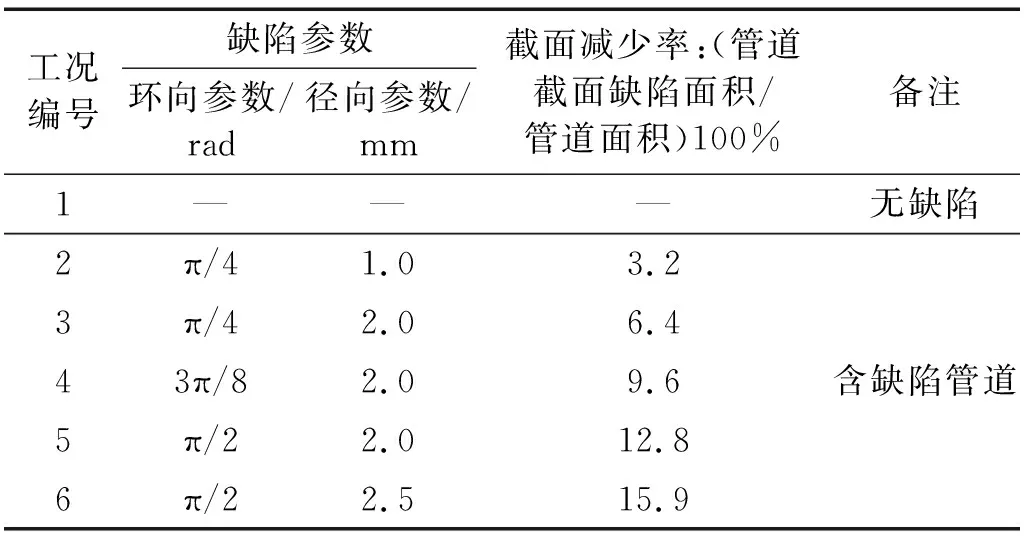
表1 含缺陷管道的实验工况Tab.1 Experimental conditions of defective pipeline

图6 三种缺陷示意图Fig.6 Three kinds of defects diagram
试验接收到的6种工况的检测信号,如图7所示。由图7可知, 6种工况下的入射波与端面回波均比较明显,可以直接观察到。对于缺陷回波,只有在缺陷较大的工况6的入射波与端面回波之间可以直接观察到,其他工况均无法观察到缺陷回波。为了提高小缺陷回波的检测灵敏度,截取入射波与端面回波之间的信号,输入到本文的检测系统中,利用Duffing系统对参数敏感以及对噪声免疫的特点对弱导波信号进行识别。
2.2 缺陷识别
由于缺陷回波的出现时刻是未知的,因此本文截取图7中入射波结束之后到端面回波出现之前的信号,本试验中即为0.5~1.6 ms的信号,按照式(3)格式输入到Duffing检测系统中,采用四阶龙格-库塔方法对检测系统进行求解,时间步长设为0.2 μs,初值设为(0,0),计算时长为800个外激励周期,计算并绘制出Poincare截面,通过观察Poincare截面判断系统的状态,进而判断待测信号中是否含有缺陷回波。
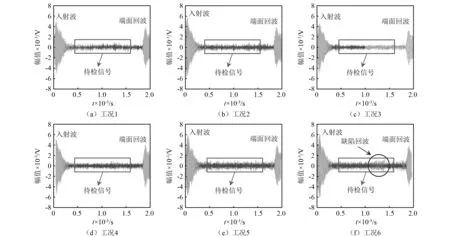
图7 试验测得信号Fig.7 Experimental signals
对于工况1完好管道,在入射波和端面回波之间没有缺陷回波,截取的待检信号为纯噪声信号,将其输入到Duffing检测系统后,系统Poincare截面如图8(a)所示,对比图2(a),可以发现噪声输入与无输入时的Poincare截面基本一致,系统仍处于周期状态,这说明噪声不会引起系统状态的变化。工况2的结果,如图8(b)所示,可以看到Poincare截面开始出现分布密集的点集,系统表现出了弱混沌特征,这是因为缺陷回波与检测系统的频率相同,叠加之后,相当于改变了驱动力幅值,使系统由周期态进入了混沌态,该结果图与输入纯噪声信号可以明显的区分开来。工况3的结果如图8(c)所示,Poincare截面出现沿着一条弧线分布的密集点集,呈现出了一定的层次结构,说明系统已经进入混沌态。工况4~工况6的计算结果如图8(d)~图8(f)所示,系统的Poincare截面均呈现出了混沌的特征,这说明待测信号中均含有缺陷回波。在本试验中,缺陷导致的截面损失率大于12.8%时,可以通过直接观察试验信号的方式检测缺陷,利用本文的检测系统最小可以识别截面损失率为3.2%的小缺陷,显著提高了管道小缺陷检测灵敏度,且系统对噪声具有一定的免疫力。

图8 实测信号输入到系统后的Poincare截面Fig.8 Poincare section after experimental signals is input into the system
2.3 缺陷定位与评估
张伟伟等研究表明,不同长度的导波信号均会引起系统状态的变化,与信号的完整性无关,因此可以采用二分法对待测信号逐级分解,利用Poincare截面判断系统状态,逐步定位缺陷回波信号出现的时刻,具体步骤如下:
步骤1将待测信号进行长度归一化,即将信号长度视为1;
步骤2将信号平均分为长度为0~0.5的A信号与0.5~1.0的B信号;
步骤3将A信号输入到检测系统中,观察Poincare截面,若发生变化,则将A长度归一化,进行下一级分解;
步骤4若A信号输入到系统中,Poincare截面未发生变化,则按照步骤3分析B;
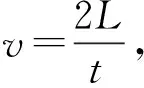
(6)
由于试验中管道总长一定,即L=5 m,t=18.3 ms,只需识别出tc,即可依据式(6)估算出缺陷位置。以下我们以工况2为例,说明二分法的使用。由于本例中截取信号时间间隔为0.5~1.6 ms,二分过程如表2所示。
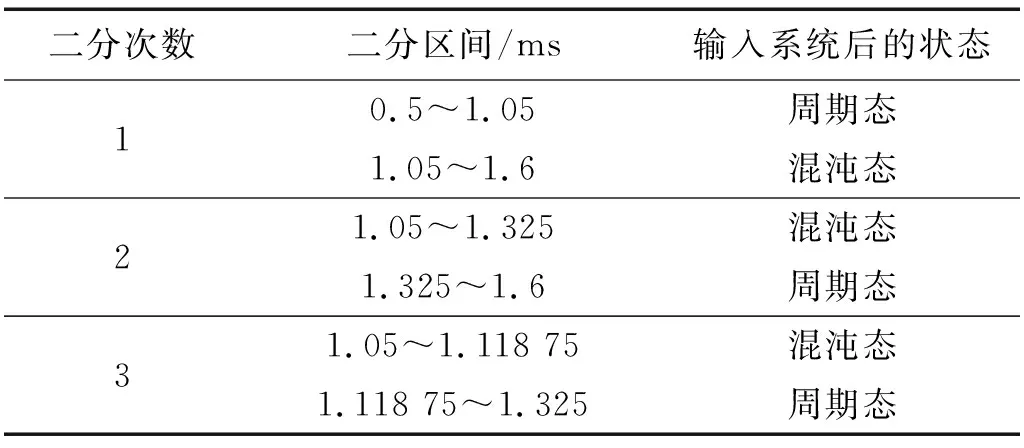
表2 二分法损伤定位Tab.2 Damage localization by dichotomy
由表2可知,经1次分解后发现,0.5~1.05 ms信号并未使系统状态发生变化,而1.05~1.6 ms使系统进入了混沌态,说明1.05~1.6 ms中含有缺陷回波;继而对1.05~1.6 ms的信号进行第2次二分发现,1.05~1.325 ms区间的信号导致系统转变为混沌态,说明缺陷回波信号位于该区间;再对1.05~1.325 ms进行第3次二分发现,1.05~1.118 75 ms区间的信号导致了系统转变的混沌态,说明缺陷回波在该区间上。将1.05~1.118 75起始时刻与结束时刻代入式(6)中计算可得
2.87 m 取中间值为dc=2.965 m,这与预置缺陷位置3 m只有0.035 m的误差。可见只要对信号进行多次二分,即可达到满足精度要求的缺陷定位。如果在分解过程中,如果发现二分后的两段信号都会引起系统的改变,则可选择二分间断点作为波到时刻进行识别。考虑到管道中的缺陷未知,有可能存在多个缺陷回波的情况,可继续进行下一级分解,判定缺陷回波是否位于二分间断点。 此外,从图8中还可以观察到,当截面损失率增大时,缺陷回波逐渐增强,Poincare截面上点集的分布愈加分散,点集沿一条弧线分布的混沌特征愈加明显,这是因为随着驱动力幅值减小,系统由周期向混沌的转变中经历了间歇性混沌状态,即混沌与周期交替出现的状态,随着幅值减小,间歇性混沌状态中的周期部分逐渐减小,混沌部分增大,最后系统完全转变为混沌态,因此驱动力幅值的变化程度与混沌特征的强弱是有关的,利用这一特性,在Poincare截面上x∈(-2,2)内分为200份,y∈(-1.5,1.5)内分为150份,构造胞空间,共计200×150个胞元,每个胞元为0.02×0.02的正方形,如图9所示。 图9 胞空间划分示意图Fig.9 Diagram of cell space division 然后,将Poincare截面结果与该胞空间重叠,计算胞空间上有多少胞元被Poincare截面上的点所占据,被占据的胞元数记为N(index)。分析所有工况的N(index),并绘出N(index)随缺陷大小的变化规律,如图10所示。从图10中可以看出,当截面损失率小于9.6%时,N(index)与管道截面损失率之间存在简单的线性关系,这说明当缺陷回波幅值在较小范围内逐渐增大时,Poincare截面上的点数也逐渐分散,这表明间歇性混沌中的混沌部分逐渐增大,因此,可将N(index)视为损伤指标,用于缺陷大小评估。而当缺陷大于12.8%时,损伤指标N(index)的变化近似为平台,这说明当缺陷回波的幅值超过一定的量时,Poincare截面的点数不再随缺陷回波的幅值增加,而是趋于稳定,这是因为系统已经完全进入混沌状态,幅值继续减小也不会增强混沌特征,这也表明损伤指标N(index)不适合用于评估较大的缺陷。不过,对于较大的缺陷,直接从时域结果即可观察到缺陷回波,可采用多种线性方法进行识别。 图10 损伤指标与截面损失率之间的关系Fig.10 Relationship between damage index and section loss rate 针对超声导波在检测长距离管道中的小缺陷时,缺陷回波被噪声淹没难以检测的问题,本文基于Poincare截面提出了一种利用混沌系统敏感性识别弱导波信号的方法,并将其用于管道结构的小缺陷识别中。利用分岔分析确定了检测系统的参数,通过数值仿真验证了该方法的抗噪声干扰能力,通过对管道中的微弱缺陷回波信号识别实现了管道小缺陷检测。通过本文研究,得到了以下结论: (1)以Poincare截面作为混沌判据的检测系统,对噪声信号具有一定的免疫能力,对与驱动力有相同频率的导波信号却非常敏感,可识别信噪比为-29 dB的弱导波信号。 (2)确定临界状态参数是本文方法的关键所在,本文发展了一种利用系统的分岔特性确定临界状态的方法,可以快速的找到适用于弱信号检测的临界状态,结合Poincare截面设定检测系统。 (3)在实验研究中,当截面损失率大于12.8%时,才能直接观察到缺陷回波,而本文基于Poincare截面的检测系统最小可以识别截面损失率为3.2%的小缺陷。 (4)本文利用二分法实现了损伤定位,并利用系统的间歇性混沌特性,通过构造胞空间,以Poincare截面上点所占胞元数定义损伤指标,在一定范围内,该损伤指标与缺陷大小之间具有简单的线性关系,为评估缺陷大小奠定了基础。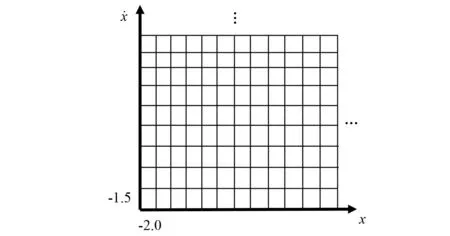

3 结 论
