基于关联规则的多冷水机组系统负荷优化分配
2022-02-16王香兰晋欣桥贾志洋
王香兰 晋欣桥 吕 远 贾志洋
(上海交通大学机械与动力工程学院 制冷与低温工程研究所 上海 200240)
空调系统在设计选型阶段为满足建筑室内热舒适性要求,同时避免出现末端冷量不足的情况,一般会按照建筑最大负荷设计,采用容量较大的冷水机组来提高空调系统在不同负荷条件下的灵活性,因此空调系统制冷能力通常有很大富裕,导致冷水机组长期在部分负荷下运行,存在能效低、能耗高的问题[1]。因此,对冷水机组的运行控制进行优化是空调系统节能的重要途径之一。
大多数空调系统均采用多台冷水机组设计,运行时一般通过控制各台机组的冷冻水供水温度及冷冻水流量实现负荷的分配。在机组型号一致的多冷水机组系统中,较多采用相同冷冻水供水温度控制,每台机组提供相同的冷量;在机组型号不一致的系统中,每台机组通常按其额定制冷量占所有运行机组额定制冷量总和的比例提供冷量[2]。Liu Zhaohui等[3-4]研究表明冷水机组性能系数(coefficient of performance, COP)与其部分负荷率(partial load rate, PLR)有关,不同机组有不同的COP-PLR关系。因此,要提高多台冷水机组系统的总能效,应根据各机组的COP-PLR关系状况优化负荷分配。
闫军威等[5]以冷水机组总能耗最小为目标,通过建立各台冷水机组运行能效模型,基于遗传算法提出了多台冷水机组负荷优化分配策略。Chang Y.C.[6-7]以冷水机组性能系数为目标函数对机组负荷分配问题建立数学模型,分别采用拉格朗日算法和Hopfield神经网络进行负荷优化分配。A.Beghi等[8-10]分别提出运用收敛速度更快、鲁棒性更好的多阶段遗传算法,改进的人工鱼群算法和交替方向乘子法来优化负荷分配问题,发现这些算法能够更快和更稳定地找到与其他算法相同或更优的最优解,并且能够取得良好的节能效果。
上述研究主要通过对机组建模,然后基于模型预测和优化算法来获取使机组总能耗最低或运行能效最高时系统的负荷分配。该类方法通常需要构建准确的预测模型来解决冷水机组负荷分配中多参数、多约束的优化问题。在实际建模过程中,由于冷水机组的非线性特性及内部结构参数难于获取的特点,模型的通用性和精度相互矛盾,实际应用较为困难。
近年来,随着楼宇自控技术及数据存储技术的发展,获取大量冷水机组系统的实际运行数据更为容易。Yu Zhun等[11]等指出室外气候数据、建筑物运行数据、建筑物物理参数之间可能存在直接或间接联系,可使用关联规则挖掘发现数据之间关联性,检测设备中的故障,以此制定出建筑节能运行策略。张炜杰等[12-13]运用数据挖掘方法对上海市商业建筑中冷水机组运行数据进行分析,指出当前冷水机组运行具有很大的优化节能潜力。Yao Ye等[14]基于现场实测数据,对冷水机组各变量与冷水机组性能之间的关系进行了验证,并生成了冷水机组性能图,基于冷水机组性能图生成了冷水机组的优化控制策略。周璇等[15]通过Apriori频繁项集算法分析了各种运行工况下的单台冷水机组最佳运行能效与各运行参数之间的关联规则,以指导冷水机组的节能优化运行。
本文提出以机组运行数据之间挖掘出的关联规则替代建立机组模型,用于对多冷水机组系统进行负荷优化分配。该方法可以在数据量充足的背景下挖掘出冷水机组运行参数与机组运行能耗之间的关联性,表达形式更加直观简洁,并且基于历史运行数据形成的关联规则可以真实反映系统的运行特点,能够应用于实际工程项目中。
1 研究对象
本文选取某工厂自动化生产车间的多冷水机组系统作为研究对象,系统结构如图1所示。
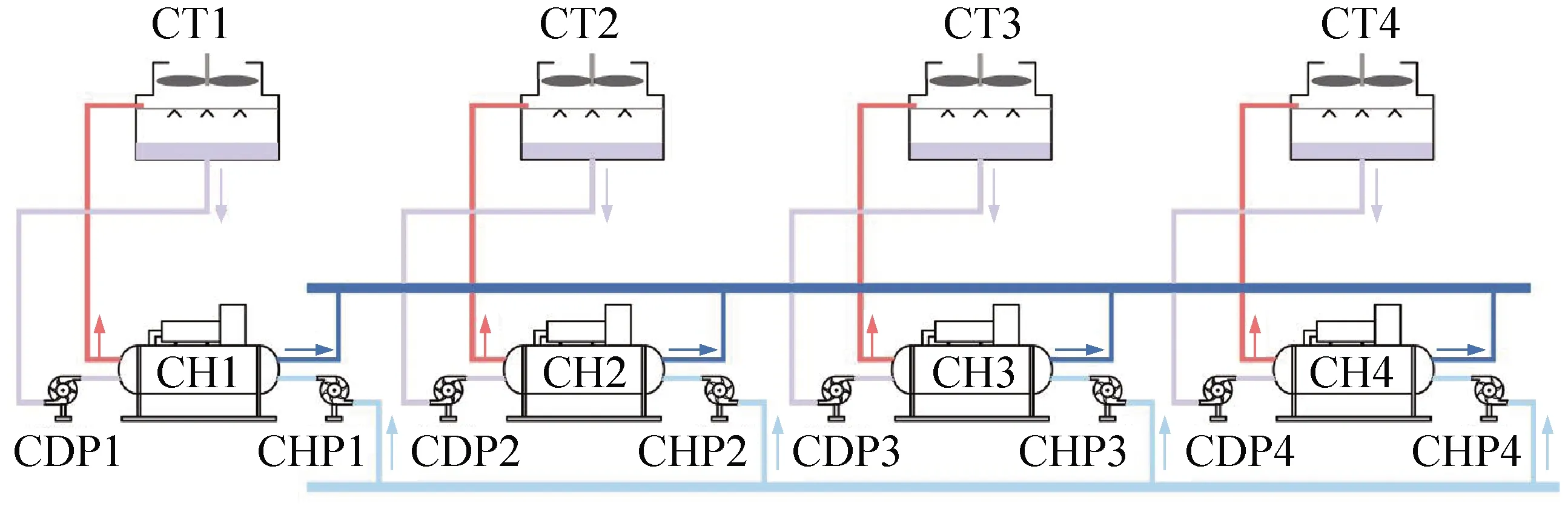
图1 多冷水机组系统
多冷水机组系统由4台(CH1~CH4)并联离心式冷水机组组成,其中,CH1和CH2为相同型号,CH3和CH4为相同型号;每台机组都独立配套型号相同的变频离心式冷冻水泵(CHP1~CHP4)、变频离心式冷却水泵(CDP1~CDP4)、湿式冷却塔设备(CT1~CT4)。系统设备基本信息如表1所示。
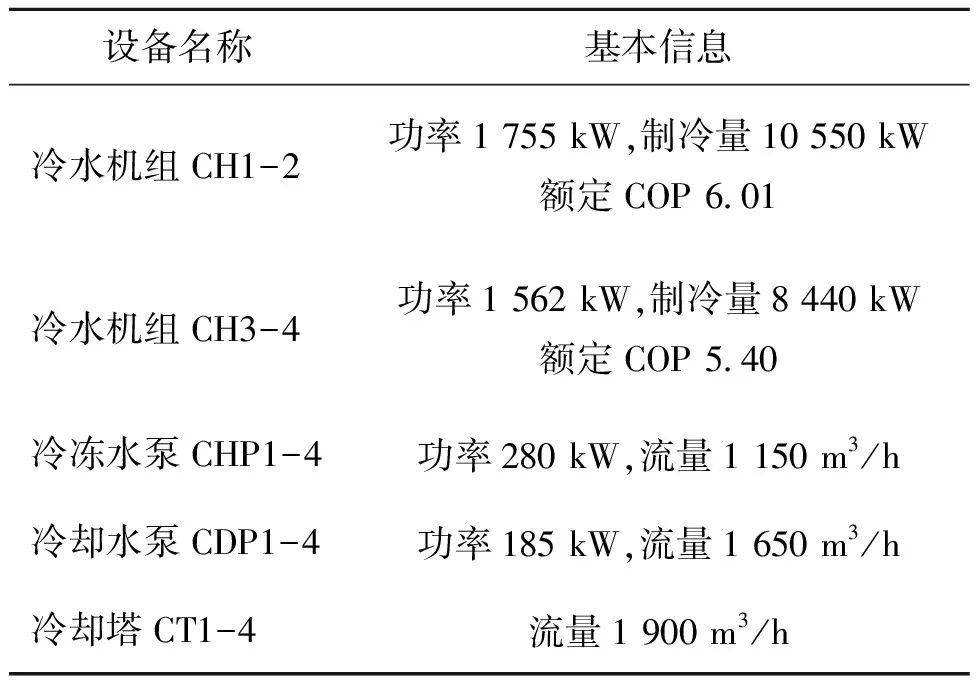
表1 冷水机组系统设备基本信息
本研究系统中,分别在室外环境、各台冷水机组、冷冻水泵、冷却水泵和冷却塔处布置了温度传感器、流量传感器、电功率表等多种数据监测设备,共采集了从2019年8月1日至2019年9月20日的72 344条数据,采集时间间隔为1 min,包括室外干湿球温度、各台设备启停信息、各台机组冷冻水供回水温度、冷却水进出水温度、机组运行功率、水泵运行频率与功率、冷却塔风机运行频率与功率等运行参数。
2 运行数据处理
因受到动态运行、噪声干扰、传感器异常、通信中断等多种因素的影响,实际冷水机组系统的运行数据可能存在非稳态、数据缺失和数据异常等问题。因此使用这些数据以前,需要根据不同类型的数据问题,采用不同的数据处理方法进行数据筛选和清洗。针对缺失数据,由于在本文获取的数据中缺失记录仅约占总数据的3%,因此对含有缺失数据的记录采用直接删除的方法;由于本文主要研究机组稳定运行时的性能特征,因此使用移动窗口算法筛选出各台设备的稳态数据;针对异常数据的识别与清洗问题,采用孤立森林算法将数据划分成不同维度进行分析处理。
2.1 基于移动窗口算法的稳态数据筛选
由于运行工况、设备启停等动态影响,采集的数据中通常会包含部分非稳态数据。使用基于数理统计原理的移动窗口算法[16],可以依据时间序列快速精准地筛选出稳态运行数据。
图2所示为2019年8月6日00∶00至8月8日00∶00期间冷水机组CH1的制冷量随时间的变化,并将以此为例介绍移动窗口算法原理。由图2可知,在机组启动后,制冷量变化幅度较大,经过一段时间后制冷量才相对稳定。移动窗口算法的目的就是在选定某一筛选参数的前提下,沿着时间序列移动,基于窗口内数据标准差与给定标准差阈值之间的关系,判定移动窗口一侧新加入的数据是否为稳态数据,通过窗口的不断移动,将所有稳态数据筛选出来。
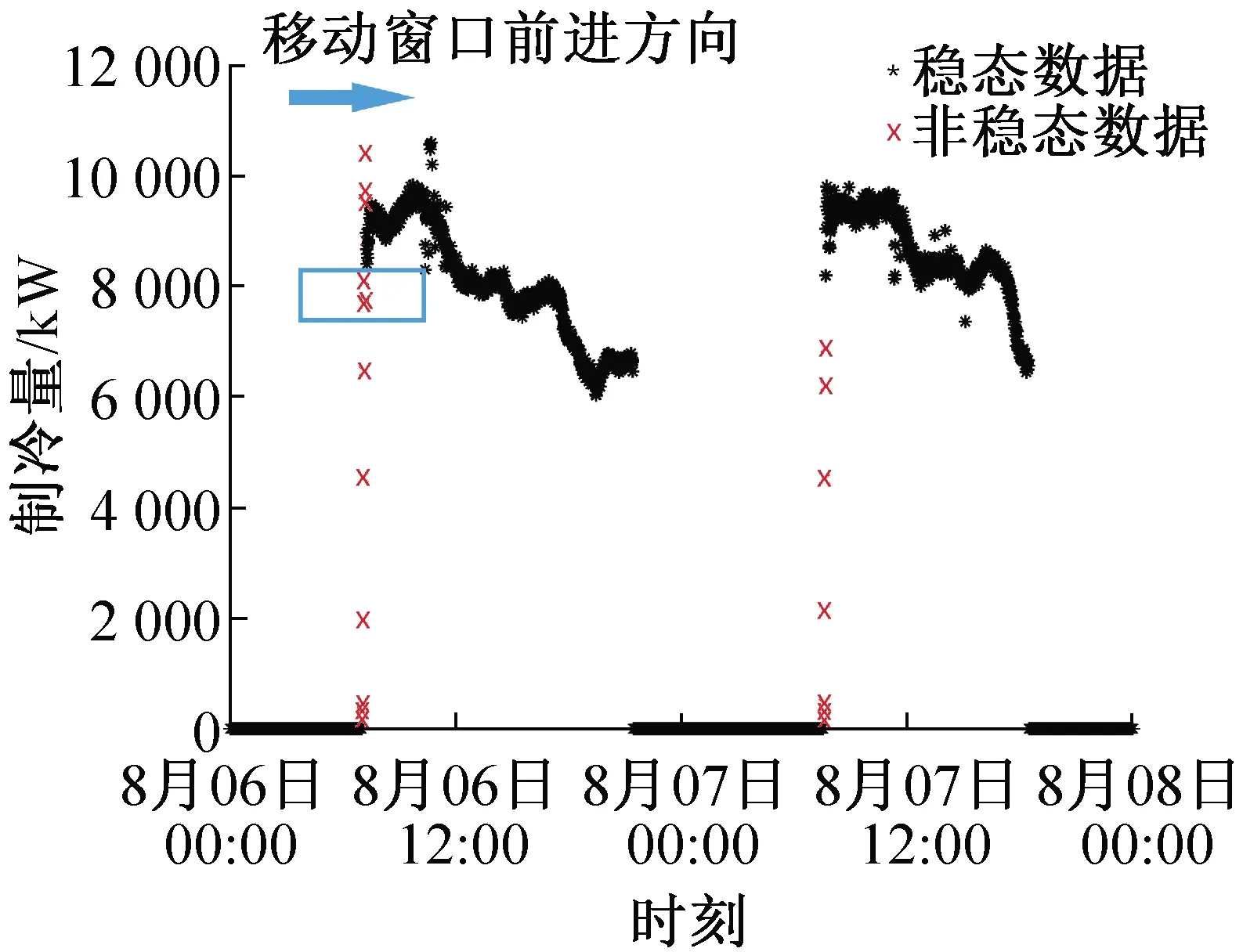
图2 移动窗口算法原理
对于本文所研究的多冷水机组系统而言,与同一台机组串联的冷冻水泵、冷却水泵和冷却塔等设备均同步启停,因此选取各机组制冷量作为各机组某条数据记录的稳态筛选参数。首先根据各台机组单独的运行数据筛选出某一时刻下该机组处于稳定运行的数据记录,然后根据数据记录中的时间特性将各台机组的稳态数据记录进行整合,即同一时刻可能出现某些机组稳态运行,某些机组停机的情况。最终通过移动窗口算法,从原始72 344条总数据中整合筛选出了60 136条稳态数据记录。图3所示为CH1进行稳态数据筛选且处于运行状态下的数据结果。
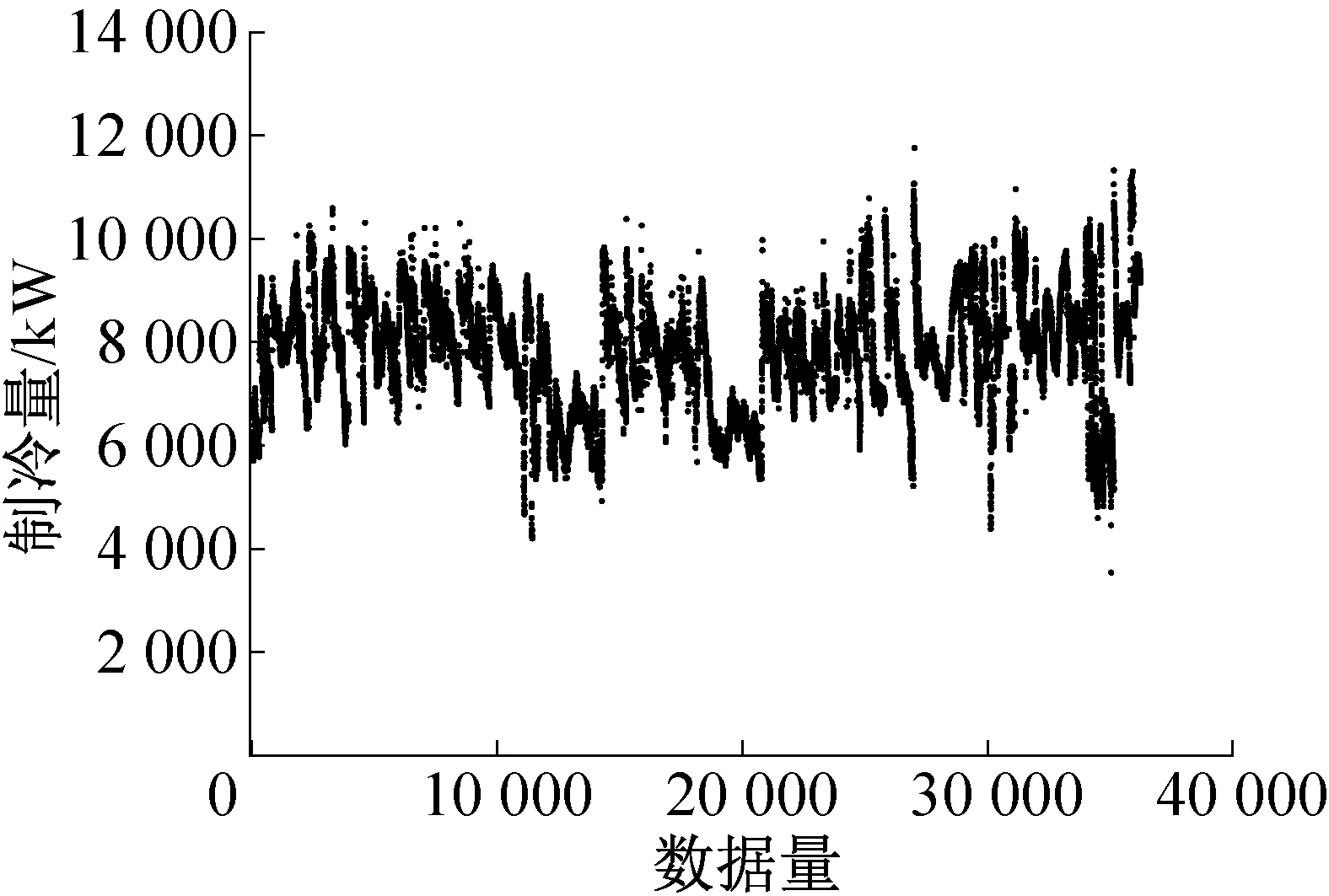
图3 CH1稳态筛选后数据
2.2 基于孤立森林算法的异常数据识别
孤立森林(Isolation Forest)算法使用孤立树的二叉搜索树结构,分别对某棵树上的n条d维样本数据进行孤立,即从根节点开始,在每个节点处随机选取d个维度中的某个维度dj以及该维度范围内的一个分隔值pj,将当前节点处的样本数据按照该维度下的分隔值pj进行二叉切分。由于异常值的数量较少且与大部分样本较为疏离,因此异常值会被更早的孤立出来,即异常值会距离根节点更近,而正常值则会距离根节点更远。基于异常数据能够较早停止切分的特征,利用训练好的Ψ棵孤立树,将数据集X中每个数据点xi遍历每一棵孤立树,根据各棵树上建立的数据二叉切分关系,对该数据点在每棵孤立树上从根节点到最终所在的叶节点处的路径长度取平均值,并通过归一化路径长度来定义样本xi归一化后的异常分数s(xi,n),异常分数的计算如式(1)~式(3)所示,最后通过设置异常分数的阈值来判别异常数据。
(1)
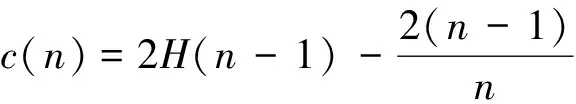
(2)
H(n-1)≈ln(n-1)+γ
(3)
式中:s(xi,n)为归一化后的样本点xi的异常得分;c(n)为样本个数为n的孤立树的平均搜索路径长度;hj(xi)为样本xi在第j棵孤立树上的路径长度;E(hj(xi))为样本xi在各棵孤立树上的路径长度平均值;H(n-1)为谐波数;γ为欧拉常数,取值为0.577 215 664 9。
由于每一条数据记录中同时包含着冷水机组、冷却水泵、冷冻水泵、冷却塔、外界环境等多种参数,因此需要根据具体研究目标对数据维度进行选择,提高数据处理速度。以冷水机组为例,由于与冷水机组相关的运行参数较多,因此可以按照机组的运行特征和数据特点,将冷水机组相关数据分为三组进行分别检测,分别为:1)冷冻侧:蒸发温度、冷冻水供水温度,冷冻水回水温度;2)冷却侧:冷凝温度、冷却水进水温度、冷却水出水温度;3)制冷量、机组能耗。最后在将各组中识别出的异常数据记录取并集,获取某台冷水机组的所有异常数据记录。图4所示为在异常分数阈值设置为0.7时,CH4的冷却侧异常数据识别结果,从图中数据分布情况可知,孤立森林算法能够较为精准地识别出多维数据中的异常值。
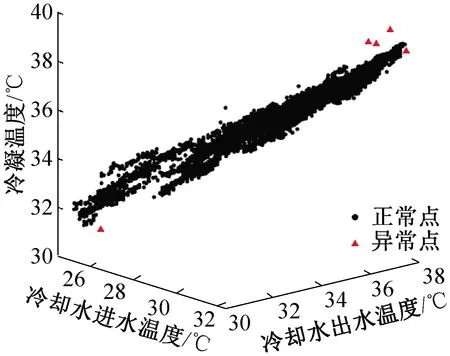
图4 CH4冷却侧数据异常值检测结果
3 基于关联规则的优化参数挖掘
为了降低机组运行的总能耗,实现多台冷水机组的负荷优化分配,本节基于预处理后的实际运行数据,采用关联规则挖掘算法建立“外界工况—机组能耗—优化参数”的关联规则,分析在不同外界工况的实际数据下,各台冷水机组能耗较低时所对应的优化参数。
3.1 关联规则挖掘
3.1.1 关联规则
关联规则挖掘(association rules mining, ARM)是一种无监督的机器学习方法,可以从大量数据中发现事物、特征或者数据之间频繁出现的相互依赖和关联的关系,得出形如“由于某些事件的发生而引起另外一些事件的发生”之类的规则。
关联规则的形式通常为:X→Y,(Sup,Conf)。其中X和Y为事务集D中两个独立不相同的非空子集,均包含若干个项集,X称为前提,Y称为结论。Sup和Conf分别为某一条关联规则的支持度和置信度,分别体现关联规则的重要性和可靠性,按照式(4)~式(5)计算获得。
Sup=support(X→Y)=P(X∪Y)
(4)
(5)
式中:Sup为支持度,表示X和Y同时发生的概率;Conf为置信度,表示在X发生的条件下,X和Y同时发生的概率,本质上是条件概率P(Y|X)。
支持度大于或等于最小支持度minS的项集称为频繁项集,反之称为不频繁项集;当利用最小支持度阈值从数据库中找出所有频繁项集后,再根据设定的最小置信度阈值minC可以从这些频繁项集中生成规则。
3.1.2 Apriori频繁项集挖掘算法
Apriori算法是最为典型的频繁项集挖掘方法,是利用已产生的k-项集来探索(k+1)-项集的逐层迭代方法。首先,根据最小支持度产生频繁1-项集L1,然后对L1中任意两个项集依次进行组合,将生成的候选项集在事务集中进行一次扫描,根据最小支持度产生频繁2-项集L2。重复该过程,直至某个r值使频繁r-项集Lr为空。在此基础上可以直接从已产生的频繁项集中搜索满足置信度阈值的强关联规则。图5所示为Apriori算法获取频繁项集的流程。
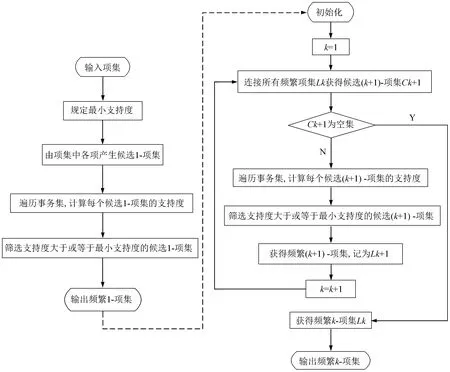
图5 Apriori算法获取频繁项集的流程图
3.2 挖掘目标与流程
本文采用Apriori算法分别挖掘每台机组对应的“外界工况→机组运行能耗”和“机组运行能耗→优化参数”的频繁项集,再根据设定的置信度获取“外界工况→可靠的最低运行能耗→可靠的优化控制参数”的关联规则,形成以数据指导控制的优化设定。
3.2.1 数据离散化
由Apriori算法原理可知,该算法在寻找频繁项集时,只能处理离散型变量之间的关系,而冷水机组系统中的测量参数通常是连续变化的,因此需要对各参数进行分区段离散化,以此找出各个离散数据区段之间的对应关系[15]。
考虑到机组运行数据具有测量不确定性、测量误差等因素,同时根据各运行数据在一定时间间隔内的变化范围情况以及数据分布特点,按照表2中的区间划分情况,将连续属性的值域等区间长度划分为多个互不重叠的区间。
3.2.2 关联规则挖掘流程
以不受系统直接或间接控制影响的室外干球温度、室外湿球温度、CH1/CH2机组或CH3/CH4机组承担的冷负荷这三个参数作为外界工况,根据表2中的划分方法,对所有运行数据进行离散化。由于数据量较大,因此需要设定较小的支持度阈值来挖掘出较多的频繁项集,经过多次试验,最终选用0.1%作为支持度阈值。

表2 相关参数离散化
图6以CH1/CH2的部分数据为例,展示了各台机组从原始数据集到获取某一工况下优化参数的关联规则挖掘流程,主要分为三个步骤:
1)Step1:数据集→“外界工况→各台机组能耗”的频繁项集。
选取离散化数据集中各台机组运行时对应的外界工况和机组运行能耗数据,使用Apriori算法,以三个外界工况参数作为前提参数,以各台机组机组运行能耗作为结论参数,挖掘出各台机组中满足0.1%支持度阈值要求的“外界工况→各台机组能耗”的频繁项集。
2)Step2:频繁项集→置信度大于阈值的能耗最低的关联规则。
针对某台机组而言,在某个确定的外界工况下可能对应着多种机组运行能耗数据。图6的Step2展示了CH1/CH2频繁项集中某一种外界工况组合情况下对应的15个能耗区间范围以及相应的置信度。由各能耗区间下的置信度可知,如果仅以某一工况对应的历史数据中出现的最低能耗运行点作为该工况的优化运行点,那么在实际系统中即使按照该点对应的优化参数进行控制,也不一定能保证大部分情况下可以获取该点的运行能耗,即需要考虑到该优化运行点出现的概率,以保证优化结果的可靠性。
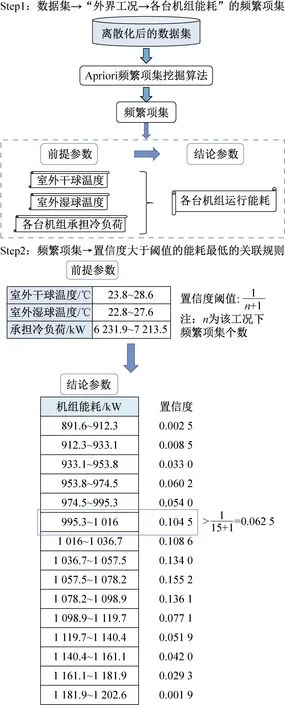
图6 关联规则挖掘流程
因此本文提出了基于关联规则寻找每台机组可靠的较低能耗的方法。首先从“外界工况→机组运行能耗”的所有频繁项集中选取外界工况条件相同的各条频繁项集,其次将该工况下机组能耗区间范围按照从低到高的顺序进行排列,选取置信度大于置信度阈值并且能耗值最低的区间范围作为该工况下的关联规则。
最终从CH1/2和CH3/4的频繁项集中分别挖掘出了64条“外界工况→可靠的最低运行能耗”的关联规则,用来体现在某种外界工况下,机组运行能耗较低的可靠情况,如表3所示。
3)Step3:能耗最低的关联规则→置信度最大的控制参数项集。
针对各台机组挖掘出的“外界工况→可靠的较低机组运行能耗”的所有规则,再次使用Apriori频繁项集挖掘算法,以每条规则中的参数为前提参数,以4个控制变量(冷冻水供水温度、冷却水进水温度、冷冻泵供电频率、冷却泵供电频率)为结论参数,挖掘“可靠的最低运行能耗→可靠的优化控制参数”的频繁项集,在相同外界工况和运行能耗下选取置信度最高的控制参数组合作为优化参数。最终各台机组分别生成了64条“外界工况→可靠的最低运行能耗→可靠的优化控制参数”的关联规则,每条规则下对应的控制参数范围如表3所示,在后续的仿真中以区间中值作为优化控制点来指导各台机组的优化运行。
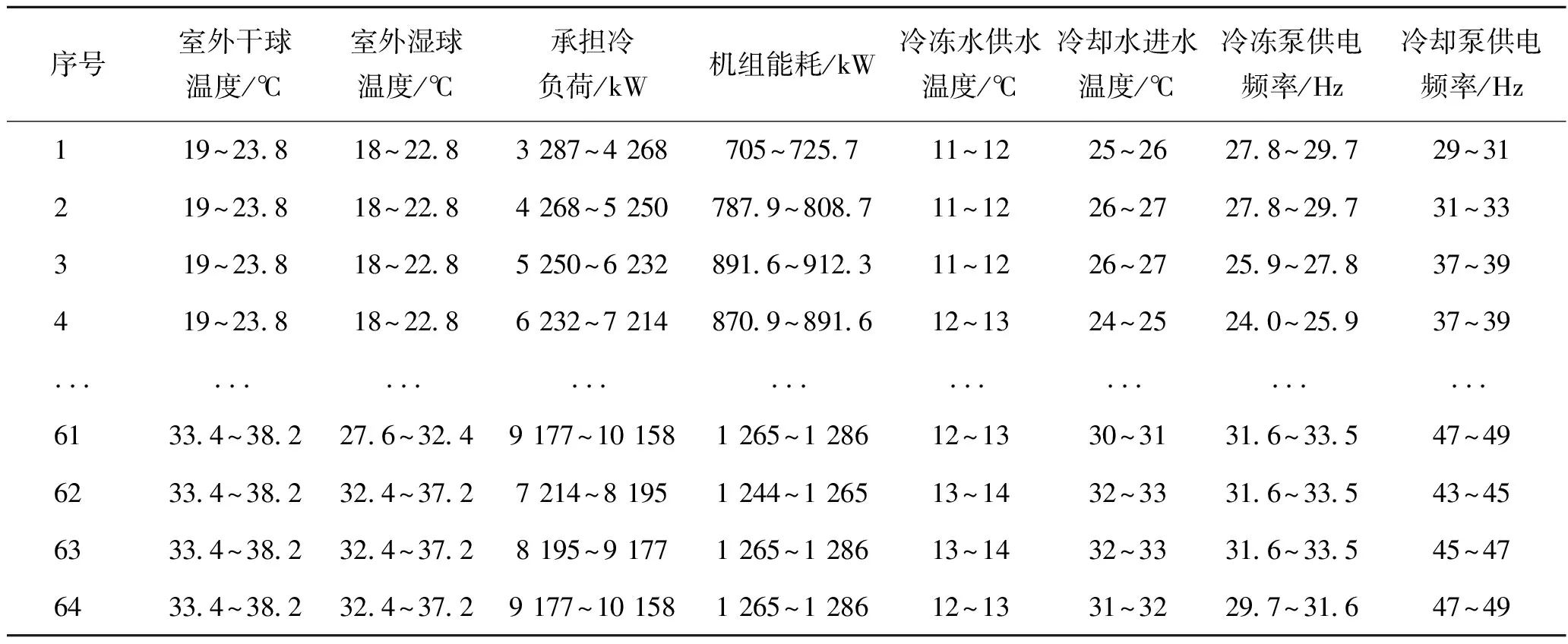
表3 CH1/2的部分关联规则
4 基于关联规则的负荷优化分配方法
通过3.2.2小节中两级关联规则挖掘可以获取各台机组在某一个外界工况下较低的能耗运行数值以及对应的优化控制参数。当某一时刻总冷负荷需求开启一台机组即可承担时,可以直接使用上述关联规则表进行优化控制,但针对一台机组无法满足总负荷需求的情况,通常需要运行多台冷水机组,并合理分配各台机组承担的负荷量以降低机组总的运行能耗。
4.1 优化负荷分配的目标函数与约束条件
以本研究系统中的4台冷水机组运行总能耗最低为目标函数,使用各台机组能耗与室外干湿球温度和承担负荷之间的关联规则替代冷水机组模型对目标函数进行最佳负荷分配情况的寻优,目标函数与相应的约束条件如式(6)~式(10)所示。
(6)
(7)
Pch,i=Rule(Ta,Twb,Loadi)
(8)
Loadi,min≤Loadi≤Loadi,max
(9)
λi∈{0,1}
(10)
式中:Pch,i为第i台机组能耗,kW;Pch,total为所有机组的总能耗,kW;Loadi为第i台机组承担的冷负荷,kW;Loadtotal为总的冷负荷需求,kW;Ta为室外干球温度,℃;Twb为室外湿球温度,℃;Loadi,min、Loadi,max分别为第i台机组承担的冷负荷的上、下限,kW;λi为第i台机组的启停情况,开启为1,关闭为0。
4.2 基于粒子群算法的负荷优化分配
粒子群优化算法(partical swarm optimization,PSO)是一种进化计算技术,源于对鸟群捕食行为的研究。粒子群中的每一个粒子均代表一个问题的可能解,基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。
本文将粒子群算法与关联规则相结合,相比于基于机组模型的参数寻优,该方法能够快速有效获取优化参数,其中粒子群算法中的相关参数如表4所示,整体的算法流程如图7所示。
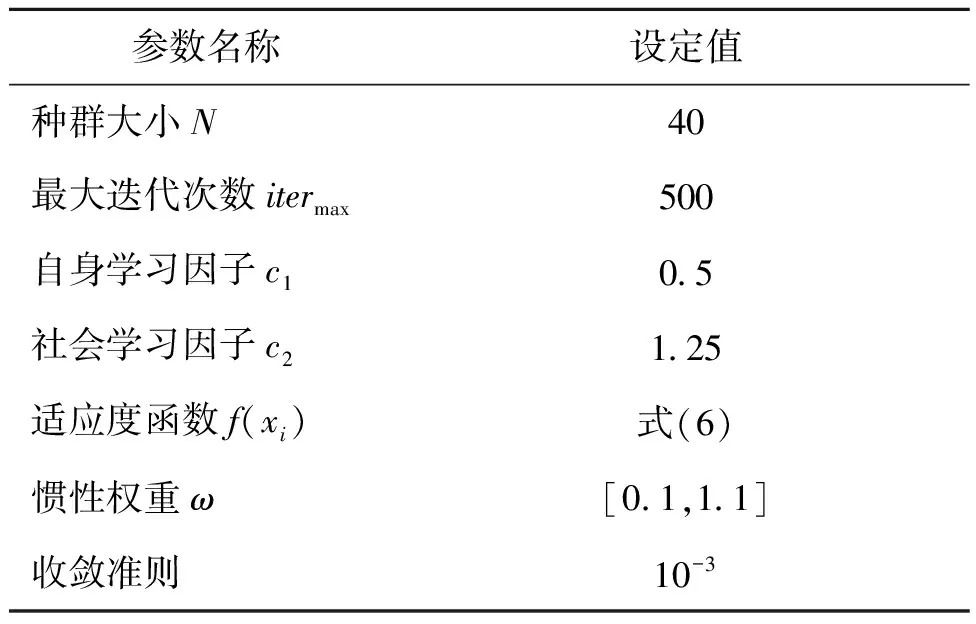
表4 冷水机组优化负荷分配控制的PSO算法参数配置
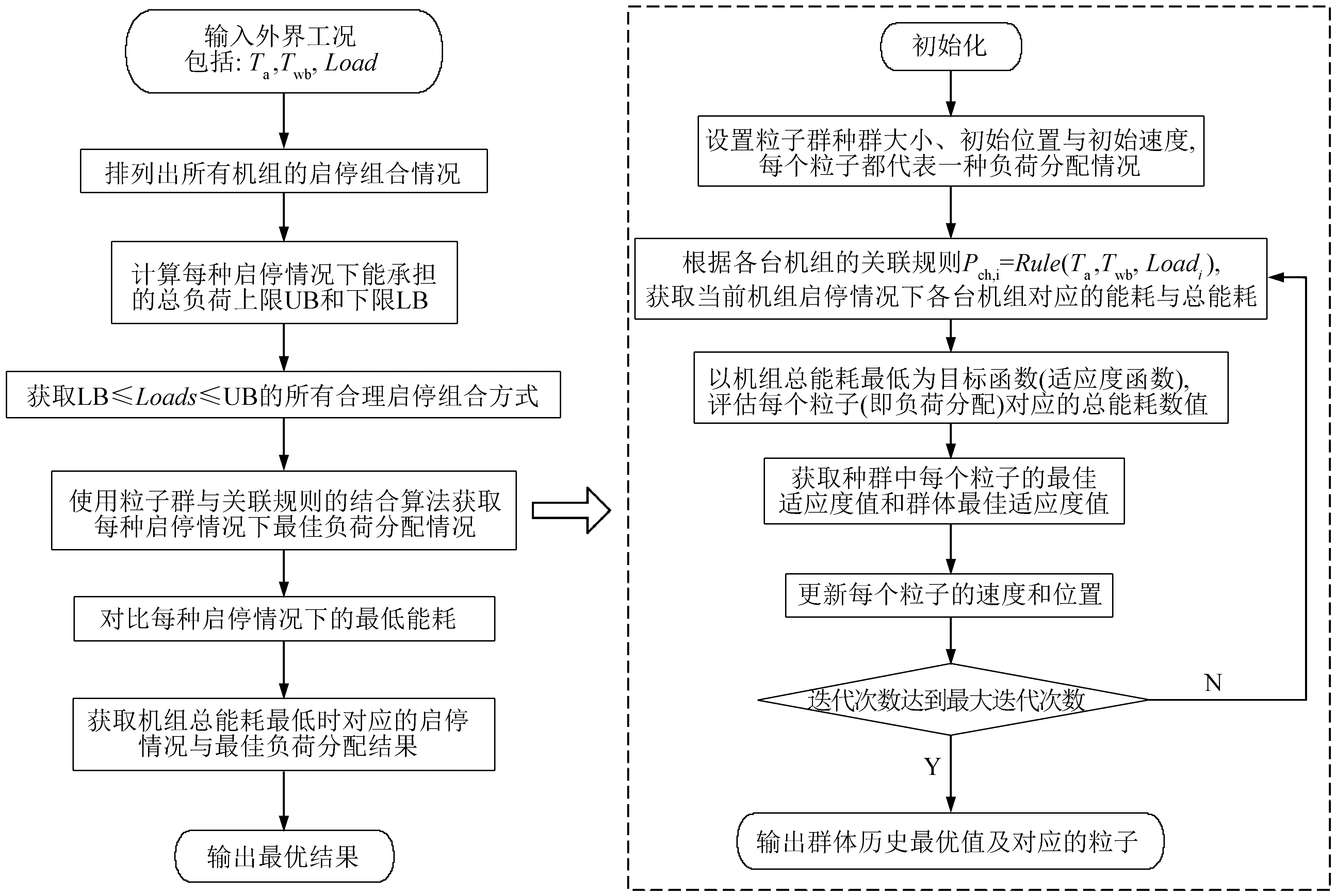
图7 粒子群与关联规则结合的负荷优化分配流程图
该算法输入条件为外界工况:室外干球温度、室外湿球温度和总冷负荷,输出为当前工况下使机组总能耗达到最低的机组启停情况以及负荷优化分配结果。首先,排列出所有的机组启停组合情况,再根据各台机组承担负荷的上下限判定每个启停组合是否满足总负荷需求,从而获取合理的机组启停组合;其次,基于关联规则的预测,采用粒子群优化算法计算每一种可能的启停组合下的最佳负荷分配及对应的机组总能耗;最后,通过对比各启停组合下机组总能耗,获取能耗最小的启停组合及负荷分配情况,利用表3的关联规则即可获得各台机组对应的优化控制参数。
5 仿真结果与分析
以2019年8月26日(夏季)07∶00—21∶00的运行情况为例,通过对比实际运行结果与本文提出的优化方法运行结果下的机组运行总能耗,分析说明本文提出的负荷分配优化算法的有效性。逐时室外干湿球温度与冷负荷需求的实测数据分布如图8所示。

图8 2019年8月26日外界工况实测数据分布
基于实测外界工况数据,将本文负荷分配的优化结果在系统仿真平台上[17]进行验证,以1 h为一次优化周期,分别对比了优化前后机组逐时总COP和启停组合及负荷分配的变化情况,结果如图9和图10所示。
由图9可知,优化后各时刻系统总COP均有所提高,说明在满足冷负荷需求的前提下,本文的负荷优化分配策略能够充分发挥节能潜力。由图10可知,优化后各时刻机组的启停组合及负荷分配相比之前发生了显著变化。如图10所示,在15∶00—18∶00时间段,优化前系统运行4台机组,而优化后只需运行3台机组,减少了机组运行数目并提高了运行机组的负荷率,由图9可知,该时间段机组总COP有显著提升。
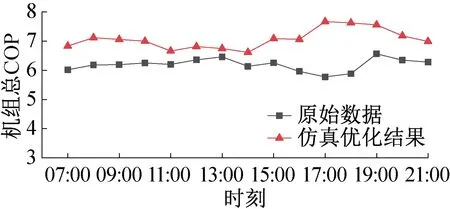
图9 机组逐时总COP优化前后对比
在其他时间段内,虽然机组的运行数量未发生变化,但机组的负荷分配却有所不同。以测试日07∶00为例,由图10可知,优化前后均开启了CH1、CH2和CH3,其中CH2承担的负荷在优化前后基本未发生变化,而CH1的负荷率则从82%降至45%,CH3的负荷率从53%升至100%。测试日07∶00时三台运行机组优化前后功率对比如表5所示。由表5可知,在该时段CH1由于负荷率降低,功率从优化前的1 179 kW降至优化后的766 kW,CH2功率在优化前后变化较小,而CH3由于负荷率增加,功率从优化前的1 128 kW升至优化后的1 144 kW,仅上升了16 kW。在该时段机组的总功率从优化前的3 510 kW降至3 093 kW,系统总COP从优化前的6.0升至优化后的6.8。
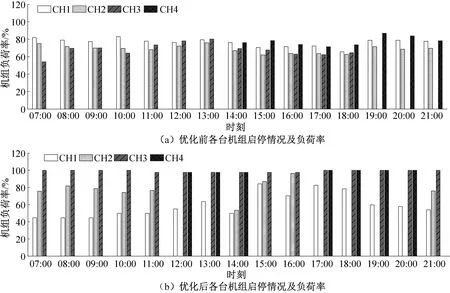
图10 优化前后机组运行组合以及各台机组负荷分配对比
表6所示为该测试日07∶00—21∶00时间段内优化前后的机组总运行能耗对比情况。由表6可知,优化后多台冷水机组系统总运行能耗降低约12.5%,表明负荷优化分配方法对于多冷水机组具有较好的节能效果。
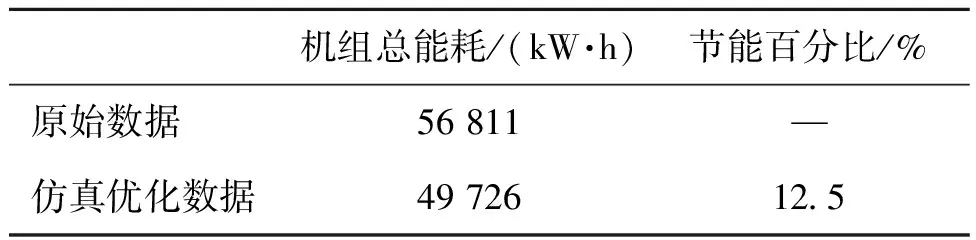
表6 优化前后机组全天运行总能耗对比
6 结论
本文以某工厂自动化生产车间多冷水机组系统为研究对象,在该系统已积累了大量运行数据的背景下,首先建立了一套完整的数据处理方法,有效筛选出非稳态数据和异常数据;其次运用预处理后的数据提出了一种基于关联规则和粒子群结合的负荷优化分配方法;最后以某一测试日为例,在仿真平台上使用该方法对多冷水机组系统进行负荷优化分配,并与原始的负荷分配情况以及能耗数据进行对比。得到如下结论:
1)通过分级挖掘方法分别获取“外界工况→可靠的最低运行能耗”和“可靠的最低运行能耗→可靠的优化控制参数”的规则,可以过滤高运行能耗对应的无用规则,有效提高关联规则的挖掘速度;并且由于关联规则是基于实测运行数据的挖掘方法,因此本文的优化方法更具可靠性。
2)与原控制方式对比,基于关联规则和粒子群算法的负荷优化分配方法能够在相同外界工况下,通过优化冷水机组的启停和负荷分配减少系统的运行总能耗。
3)测试日优化后冷水机组系统运行总能耗降低约12.5%,说明本文提出的负荷优化分配方法具有较好的节能效果。
