中央空调系统冷水机组优化控制策略研究

闫秀联，王乐唯，刘 盼，吉星星，闫秀英

（1. 西安建筑科技大学 华清学院，西安 710043；2. 西安闻泰信息技术有限公司，西安710000；3. 西安建筑科技大学 信息与控制工程学院，西安 710055；4. 西安建筑科技大学建筑设备与科学学院，西安 710055）

0 引言

能耗、电耗是反映能源效率的主要指标。电耗的影响因素相较能耗更为复杂，文献［1］分析了引起电耗上升的主要原因，其中非生产性电力消费增长较快是主要原因之一，而非生产性电力消费中居民冬季取暖、夏季制冷占空调电力负荷的很大比重。空调负荷已经成为我国夏季用电的主要负荷之一，对电力系统的稳定运行造成了极大的威胁。冷水机组是中央空调系统中消耗功率最大的部分，由于冷水机组在运行中缺乏运行优化，目前大多数建筑物的冷水机组运行都未使用最佳控制策略。对于多台联合运行冷水机组的优化控制来说，如何在部分负荷情况下，根据建筑负荷和外界环境参数的变化来优化中央空调冷水机组运行参数，从而在保证其高效运行的前提下，找到一种最佳的解决方案以降低冷水机组的能耗十分关键。

文献［2］阐述了基于BP神经网络的冷水机组制冷性能系数（coefficient of performance，COP）预测模型，分析了与冷水机组相关的运行变量的最佳值，通过采用基于遗传算法的操作变量识别，在指定范围内找到变量的最佳值，从而使冷水机组的能耗最小。文献［3］提出了一种基于多目标优化的冷水机组运行策略，用于最优冷水机组台数（OCS）和最佳冷水机组负荷（OCL）问题，实现保证室内舒适度的情况下节省供暖通风与空气调节（HVAC）系统的能量。文献［4］将交换市场算法应用于最优冷水机组负荷问题的其他优化方法进行比较，结果表明，在收敛速度和总电能消耗方面，交换市场算法比应用于冷水机组负荷方法的先前优化方法提供了更好的解决方案。文献［5］对设计中的冷却负荷分布，提出了一种鲁棒的优化设计，以选择在高部分负荷率（part load ratio，PLR）和COP下运行可能性最高的冷水机组的最佳组合。文献［6］提出了一种改进的人工鱼群算法（VAFSA）解决最佳冷水机负荷问题，使用冷却器和冷却塔的最小功耗作为目标函数，以将功耗降至最低。文献［7］研究了变负荷下的非均匀负荷匹配冷水机组并联运行特性，提出了基于能效基准的多台冷水机组控制策略，研究发现较少冷水机组并联运行时易实现较高的总体运行性能，从而达到节能降耗的目的。

1 TRNSYS仿真模型构建

以西安某既有办公建筑为研究对象搭建建筑冷负荷模型。该建筑地上24层，地下2层，建筑高度99.95m。总建筑面积70 374 m2，其中地上56 970 m2，地下13 404 m2。地上24层制冷由中央空调系统提供。冷源仿真系统模拟办公建筑1—24层空调区域，在模型建立时完全依照空调系统各个设备及空调房间相关参数进行选取和配置。作为一种简化的方法，将该办公建筑定义为24个不同的热区，每个建筑物的楼层为一个热区。

1.1 多区域建筑模型建立

在TRNSYS 中建立多区建筑模型时，需要输入建筑的长、宽、高等参数。新建建筑模型时，空调区内的设备、灯光、以及围栏参数参照图纸上给出的信息进行设置，人员负荷按上下班时间（8:00—18:00）进行设置，所需参数由设计院提供建筑设计图纸中提取。将每一层楼视为一个区域，整个楼层共24个区域，在TRN-Build建立模型，通过设置房间体积及各墙的面积参数，墙与墙之间的位置关系，反应实际建筑的三维关系。

整个冷源系统包括3台冷水机组、3台冷却泵、3台冷冻泵、3 台冷却塔，在TRNSYS 上搭建冷源系统动态仿真平台，并按照实际设备参数对部件参数进行配置。根据设计院提供的信息，得到空调系统主要设备的参数信息。搭建的TRNSYS动态仿真平台如图1所示。

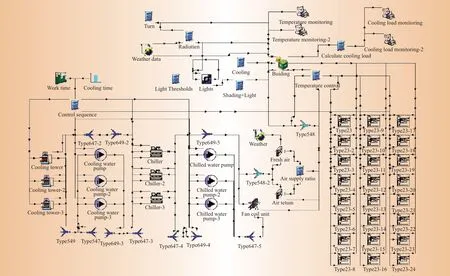
图1 TRNSYS动态仿真平台Fig.1 TRNSYS dynamic simulation platform

PID 控制器进行送风温度控制，输入参数：P=0.5、I=9.0、D=0.4。通过control card选项设置仿真时间范围与仿真步长，其中6—9 月的时间设置为3 624～6 552 h，仿真步长设置为0.1 h。Work time与Cooling time 控制设备启动时间，设备运行时间与TRN-Build中设置的运行时间相同。Work time设置设备开启时间段：8:00—18:00设为1，其余时间设为0。Cooling time设置设备运行时间范围：3 624～6 552 h。平台运行模拟6—9月室外温度变化曲线如图2所示。

图2 6—9月室外温度曲线Fig.2 Outdoor temperature curve from June to September

根据所建立模型，在Trnsys 中计算出空调区域6—9月的冷负荷需求，如图3所示。

图3 6—9月冷负荷值变化情况Fig.3 Cooling load value changing from June to September

仿真平台中设备参数与实际工程中相同，仿真得出6—9 月冷负荷峰值为4 327 kW，与设计院给出的最大冷负荷4 460 kW 对比，准确率达到97%，验证了该仿真平台的可靠性。该系统使用了3 台制冷量为1 519 kW 的冷水机组，总制冷量为4 557 kW，满足建筑最大冷负荷时的冷量需求。

1.2 冷负荷率时间频数

利用冷负荷率时间频数（cooling load rate time frequency，CLRTF）的分布来描述不同冷负荷条件与冷水机组运行时间的关系。冷负荷时间频数为不同冷负荷率下冷水机组运行的小时数与总运行小时数的百分比。分析冷负荷率可用于选取冷水机组累计运行时间最多的冷负荷率区间，进而对该区间内冷水机组运行模式进行研究。

图4给出了中央空调系统6—9月CLRTF分布图，通过仿真计算分析空调系统冷负荷与冷水机组运行时间的关系。由于冷负荷率是随运行时间变化的连续随机变量，冷负荷率的区间大小会影响冷负荷率时间频率的分布，因此，选择冷负荷率的间隔为5%。

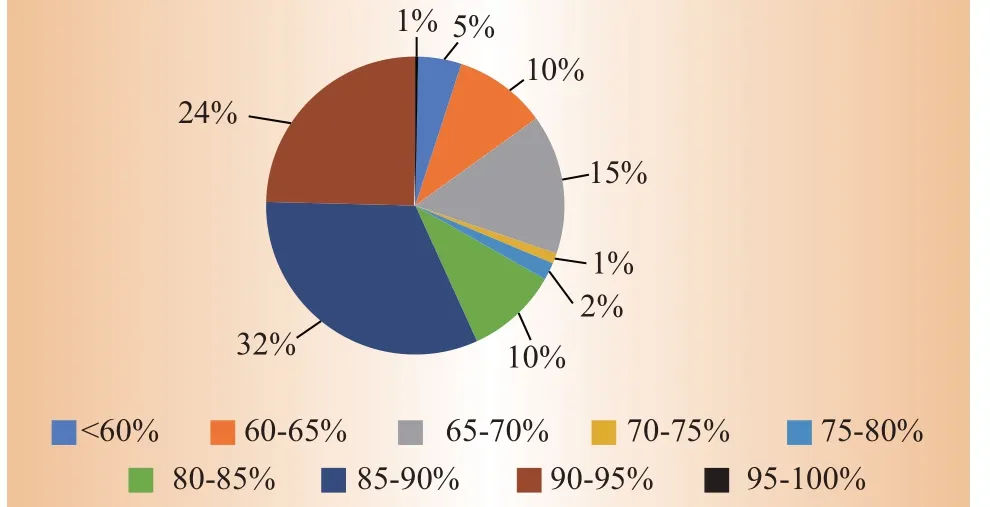
图4 6—9月冷负荷率时间频数Fig.4 Time-frequency of cold load rate from June to September

由图4 可知，冷负荷率在85%～90%的情况下，空调系统累计运行时间最多，其时间频数为32.04%；在冷负荷率为95%～100%的范围内，空调系统累计运行时间最少，其时间频数为0.3%。综上，选取累计运行时间最大的冷负荷率区间85%～90%内的工作日用以研究冷水机组运行模式。

2 冷水机组部分负荷率优化

2.1 COP 与PLR 回归模型建立

首先对COP-PLR进行线性检验，对COP和PLR的残差和拟合值进行分析。在这项研究中，散点图具有非线性或曲线结构，因此拟合值是非线性的，对COP-PLR进行非线性回归分析。

将冷水机组承担每个部分负荷率值，即PLR，用作自变量，COP用作因变量。通过不同的函数对两者进行数据拟合分析，找到最佳拟合模型与参数，说明COP与PLR之间的关系。

COP-PLR的四阶多项式回归模型如下

对高斯函数模型进行计算求解拟合，得α0、α1、α2的值分别为5.63、0.75、0.73。

绘制计算拟合所得到的多项式方程曲线，如图5所示。

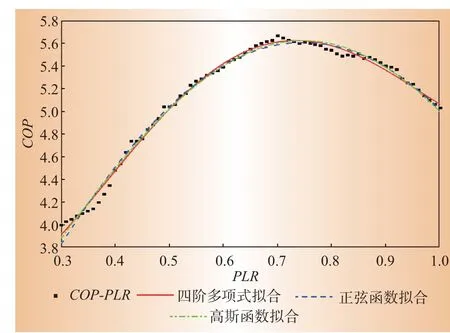
图5 冷水机组COP-PLR 拟合曲线对比Fig.5 Comparison of chiller’s COP-PLR fitting curve

由图5可知，多项式拟合、正弦函数拟合和高斯函数拟合均能较好说明COP与PLR之间的关系。对3 种拟合方式进行回归评价，R2分别为0.993 5、0.990 7 和0.991 8，RMSE值分别为0.413 5、0.487 4和0.457 6。R2都几乎为1，说明这3 个回归模型很好地拟合了数据。RMSE值都几乎为0，意味着回归模型可以被认为是正确的。其中，四阶多项式拟合模型准确度更高，更能较好的体现出COP与PLR的关系，经查F检验临界值表（显著水平：α=0.05）得F0.05(4,66)=2.511，可知F远大于F0.05(4,66)。因此，该COP-PLR四阶回归模型的置信度达到95%，说明该回归模型的适用性非常好。故选取该四阶多项式拟合方程作为COP-PLR的拟合模型。

2.2 目标函数建立

目标函数的建立，需要考虑用户侧电负荷和冷负荷的需求情况，即空调冷负荷值的变化情况。在满足需求侧负荷变化的前提下，使目标函数即冷水机组的总能耗降低。基于冷水机组系统总能耗方程与所建立的COP-PLR模型，以系统冷水机组总能耗最小建立目标函数，对目标函数中的决策变量PLR进行寻优，优化目标即为获取总能耗Pall的最小值。

目标函数如下

式中：Qn为第n台冷机的额定制冷量，kW；PLRn为第n台冷水机组的负荷率；CLall为整个系统的冷负荷，kW。

根据冷水机组设备运行限制条件，在运行过程中，每台冷水机组的PLR不能低于0.3，在解决冷水机组最优负荷率问题时需考虑到无法操作的区域限制，将冷水机组的PLR进行约束，PLR的可行域为

对该运行模式下的冷水机组运行情况进行仿真，选取冷负荷率85%～90%区间内的某工作日为例。通过TRNSYS动态仿真平台分别模拟了优化前和优化后冷水机组的总能耗变化情况。该工作日室外温度与空调冷负荷值随时间变化情况如图6所示。

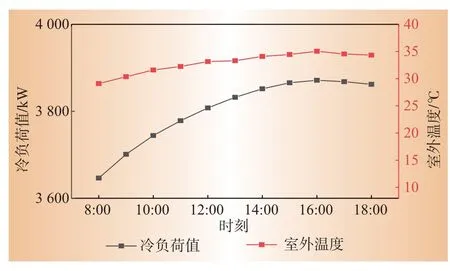
图6 工作日室外温度与冷负荷值Fig.6 Outdoor temperature and cooling load values in working days

2.3 改进混合遗传算法

改进的遗传算法用于快速提高规划方案的质量，邻域搜索用于后续的小规模优化。改进遗传算法使用启发式策略来构造初始种群，从而确保初始种群可以成功执行的任务数量和总体收益。选择操作使用锦标赛选择和最优解保留策略来计算种群。改进遗传算法中有最大未修改代数的算法终止机制，以确保在进一步改善规划结果时可以结束算法，并进入邻域搜索过程。完成邻域搜索后进行最优解保留和更新种群操作，避免陷入局部最优。其改进混合遗传算法流程如图7所示。

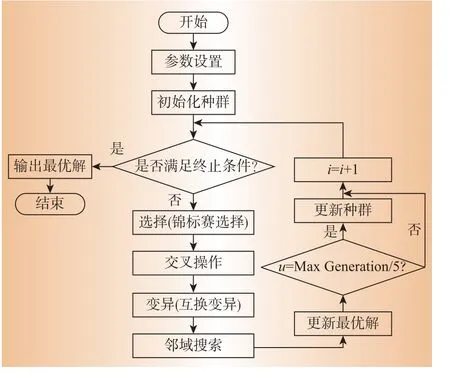
图7 改进混合遗传算法流程Fig.7 Improved hybrid genetic algorithm flow

3 冷水机组控制优化结果与分析

本文采取基于需求响应的优化控制，在室外温度较低时，可以适当提高供冷负荷。利用墙体、家具等的储能特性，在室外温度较高时可以减少供冷量。在供冷负荷峰值到来之前，可以将一部分冷负荷迁移，使供冷负荷分布在一定范围内，进而达到减小冷水机组能耗的目的。

3.1 冷水机组逐时部分负荷率

利用IGA-NS算法对该工作日每台冷水机组所承担的部分负荷率进行优化，得出各个时段的每台冷水机组部分负荷率，图8给出了3台冷水机组PLR的变化情况。

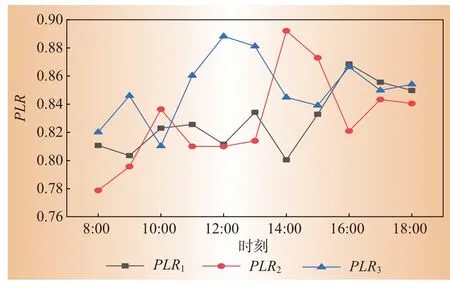
图8 基于IGA-NS算法的负荷分配率Fig.8 Load distribution rate based on IGA-NS algorith m

基于IGA-NS 算法的负荷分配率中PLR1、PLR2和PLR3分别为第一台、第二台和第三台冷水机组所承担的部分负荷率。每台冷水机组的部分负荷率随每个时刻的冷负荷值变化的数值如表1所示。冷负荷值最大时3 台冷水机组的部分负荷率分别为0.87、0.83 和0.87，发现第一台与第三台冷水机组部分负荷率相同。

表1 3台冷水机组优化后负荷分配率Table 1 Optimized load distribution rate of three chillers

根据COP-PLR的拟合曲线可知，在负荷率0.8左右时曲线出现峰值，此时冷水机组的COP值也接近于峰值，因此优化后的冷水机组运行效率得到了提高。

3.2 冷水机组逐时COP 值

冷水机组逐时COP值是根据优化后每台冷水机组逐时负荷分配率代入COP-PLR四次多项式方程计算得出，优化后逐时COP值变化情况如图9所示。COP1、COP2和COP3分别代表3台冷水机组的COP值，由于12:00第三台冷水机组与14:00第二台冷水机组承担的负荷最大，负荷率在0.89 左右，由COP-PLR拟合曲线知当负荷率超过0.7 时冷水机组COP值开始下降，因此12:00 第三台冷水机组与14:00第二台冷水机组COP值最小。

冷水机组部分负荷率的优化主要体现在COP和运行能耗方面，优化部分负荷率将提高COP值，增加冷水机组运行效率从而使运行能耗降低，因此将IGANS和GA两种算法优化后的冷水机组COP值进行对比，如图9—图10所示。可以看出采用GA算法优化后冷水机组COP最小值为5.39，而通过IGA-NS算法优化后的COP最小值为5.43。对于冷水机组部分负荷率的优化，与GA算法相比，IGA-NS算法更具有优势。即IGA-NS优化后的COP最小值略高于GA算法。

图9 基于IGA-NS算法的COP 值Fig.9 COP value based on IGA-NS algorithm

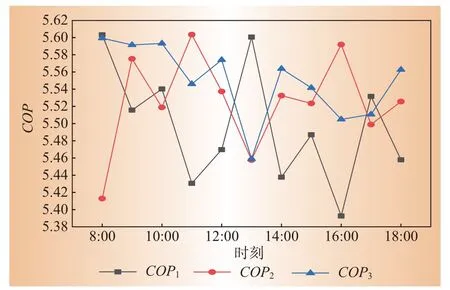
图10 基于GA算法的COP 值Fig.10 COP value based on GA algorithm

为进一步证明IGA-NS算法的优越性，将优化前的顺序控制、GA 和IGA-NS 算法控制的冷水机组的COP值求取平均值后进行对比，如图11所示。

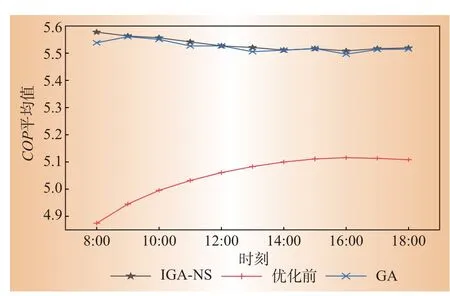
图11 优化前后COP 平均值对比Fig.11 Comparison of COP mean values before and after optimization

通过对比3台冷水机组COP平均值可以看出，大部分运行时间内，采用IGA-NS 控制COP平均值高于GA 算法控制，验证了IGA-NS 算法控制策略提高了冷水机组的运行效率。

3.3 冷水机组总能耗对比分析

3种控制方法下冷水机组全天总能耗对比结果如图12所示，采用IGA-NS算法对冷水机组部分负荷率进行优化后3台冷水机组的总能耗在8：00－18：00最低，IGA-NS算法控制下冷水机组全天最低能耗为656 kW，而GA算法控制策略下的冷水机组全天能耗最低为661 kW。两种控制算法都比优化前的顺序控制，能耗有明显降低。3种控制方法的总能耗值分别为8 280 kW（顺序），7 595 kW（GA）和7 578 kW（IGA-NS）。

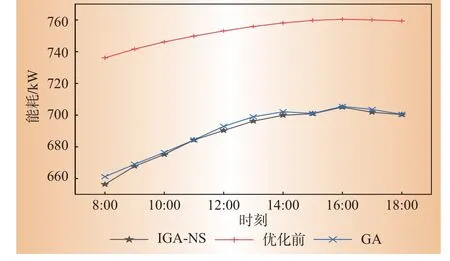
图12 优化前后总能耗对比Fig.12 Comparison of total energy consumption before and after optimization

由图12可看出，相较于原有的顺序控制和GA控制策略，采用IGA-NS算法对冷水机组PLR进行优化的控制策略在满足用户侧需求时具有明显的节能效果。全天的节能率为8.48%，CO2排放量减少700 kg。

4 结束语

目标方程与约束条件。通过基于负荷分配的台数控制冷水机组运行模式对冷机控制优化，提出了IGANS算法，对PLR进行优化。结果表明，IGA-NS算法控制的全天总能耗最小，与原有顺序控制相比，IGA-NS算法优化后冷水机组COP的最小平均值由5.11提高到5.51，不仅提高了冷水机组的COP且降低运行能耗，最终达到了提高系统运行效率并节能的效果。D