考虑实际压缩效率的NH3/CO2复叠制冷系统热力学分析

2022-02-16李连生杨启超吴家伟张永立张希良

制冷学报 2022年1期

刘利李连生杨启超吴家伟张永立张希良

(1 青岛科技大学机电工程学院青岛 266061；2 烟台市奥威制冷设备有限公司烟台 264000)

随着科技的进步和生活水平的提高，生产生活领域对低温的需求越来越多，如何安全高效地获取更低的温度，仍是制冷行业面临的主要挑战。对于蒸气压缩式制冷循环，由于制冷剂物性和压缩机压比的限制，一般采用在制取低温上更具优势的复叠制冷方式。以NH3/CO2复叠制冷系统为例，实验研究证明，在较低的蒸发温度下，相比单级NH3制冷系统和两级NH3制冷系统，NH3/CO2复叠制冷系统的COP(coefficient of performance)更高，经济性更好[1-2]。

目前对于复叠制冷系统的研究，主要围绕系统的性能优化展开。Pan Mingzhang等[3]回顾了复叠制冷系统的研究现状，系统性能的最佳值可通过调整系统低温回路的冷凝温度或高温回路的蒸发温度实现[3]。查世彤等[4]分析了NH3/CO2复叠制冷系统的最佳低温回路冷凝温度及最佳质量流量比随蒸发温度的变化。H.Park等[5]建立了预测R134a/R410A复叠制冷系统最佳中间温度的数学模型。沈九兵等[6]在考虑压缩机性能的同时，分析了R134a/CO2复叠制冷系统性能随温度工况的变化。

压缩机作为制冷系统的“心脏”，其效率的高低直接影响制冷系统的性能。在系统实际运行中，压缩机效率受工况的影响，其中容积压缩机的等熵效率与压比存在线性关系[7]。在理论研究中，为了简化计算，陈曦等[8]在分析NH3/CO2复叠制冷系统COP与工况间的相关性时，将压缩过程假设为等熵过程。贾明正等[9]分析温度工况对R1270/CO2复叠制冷系统的影响时，将压缩机总效率设置为0.7。H.M.Getu等[10]分析表明，不同压缩机效率的取值会直接影响系统性能分析的结果，因此理论分析时压缩机的效率值应贴近实际运行值。

复叠制冷系统中压缩机主要采用容积式结构，故选取体积流量的变化来代表压缩机工况变化更为准确。乔亦圆等[11]提出了级间容量比的概念，即低温级与高温级压缩机入口体积流量的比值。在其他工况一定时，赵瑞昌等[12]的分析结果表明复叠制冷系统的级间容量比存在最优值，孔帅等[13]模拟研究了工况对R134a/R410A复叠系统的级间容量比的影响。

综上所述，复叠制冷系统存在受工况参数影响的最大COP、最佳中间温度及对应的最优级间容量比。在已公开的研究文献中，主要考虑了蒸发温度、冷凝温度、复叠传热温差等对系统性能的影响，未考虑压缩机等熵效率的变化且忽略了实际运行中高低温回路的过热度和过冷度的存在。

本文搭建了NH3/CO2复叠制冷系统实验台，收集并选取与实验数据相吻合的等熵效率经验公式用于数学模型，分析了包括蒸发温度、冷凝温度、复叠传热温差、高低温回路过热度、高低温回路过冷度在内的7种温度工况参数对系统最大COP、最佳中间温度及对应的最优级间容量比的影响，并对相关参数进行了拟合分析，其中本文考虑的过热为不参与制冷的无效过热。

1 系统介绍及热力学分析

1.1 NH3/CO2复叠制冷系统原理与实验台

NH3/CO2复叠制冷系统由以NH3为制冷剂的高温回路和以CO2为制冷剂的低温回路组成，如图1所示。高低温回路通过复叠换热器耦合，复叠换热器作为低温回路的冷凝器和高温回路的蒸发器，其中NH3与CO2之间的传热温差为复叠传热温差(Td)，本文以CO2的冷凝温度为复叠系统的中间温度(TLC)。

图1 NH3/CO2复叠制冷系统原理

搭建的NH3/CO2复叠制冷系统的实验台如图2所示。系统性能的测试采用液体载冷剂法，校核实验为热平衡法；机组的运行工况范围：蒸发温度-52～-20 ℃，冷凝温度不高于40 ℃，名义制冷量为225 kW。主要部件及参数如表1所示。实验目的：以测试获得的系统COP为基础，选取较准确的压缩机等熵效率经验公式，用于多温度工况下系统性能的热力学分析。

图2 NH3/CO2复叠制冷系统实验台

表1 NH3/CO2复叠制冷系统实验台主要部件及参数

1.2 热力学分析

为了分析复叠制冷系统的性能，需要对系统进行热力学理论模拟。图3所示为该复叠制冷循环的p-h图，认为系统中的各部件处于稳定状态。计算过程进行如下假设：

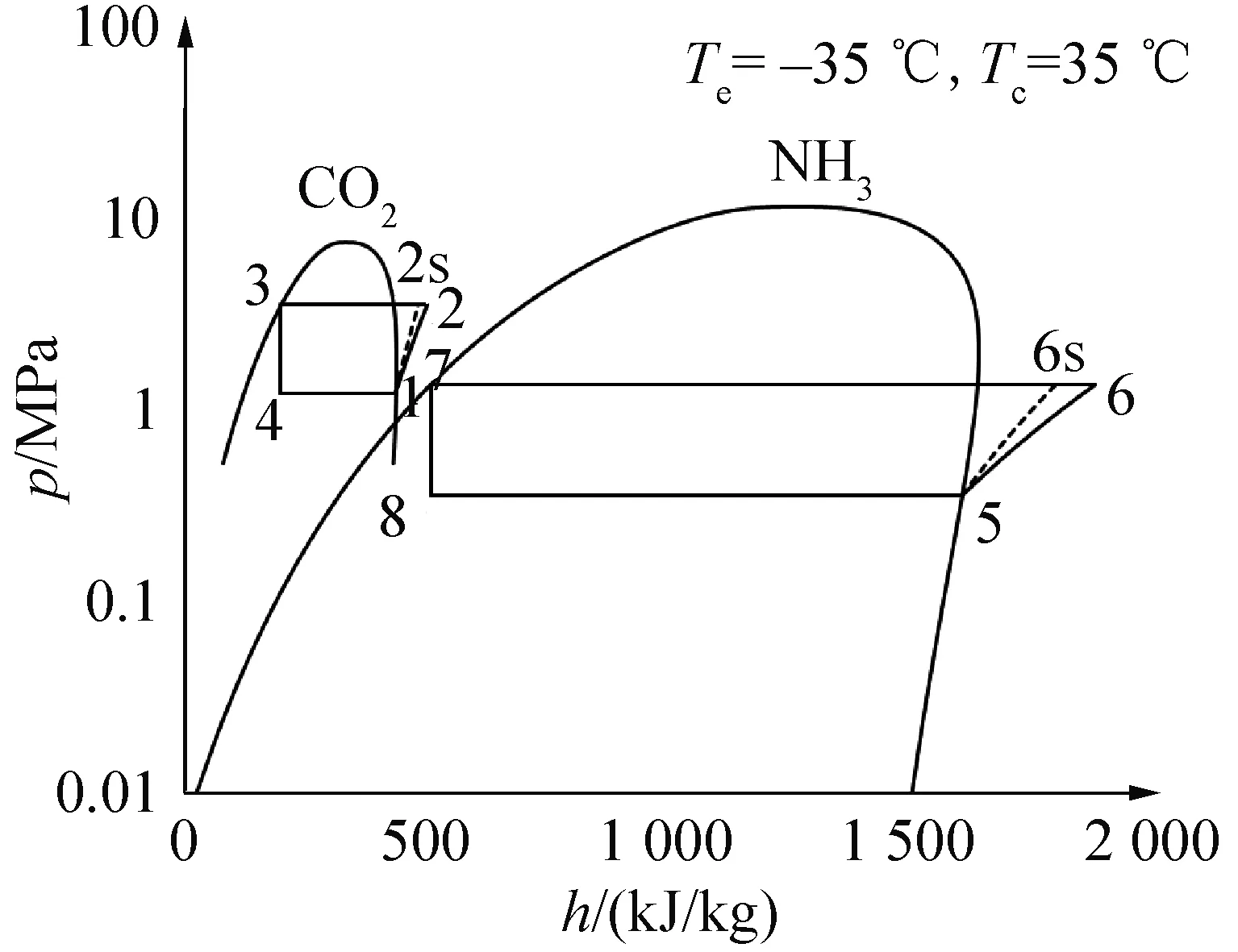
图3 NH3/CO2复叠制冷系统p-h图

1)连接各部分管路中的压降和热损可以忽略不计；

2)节流过程为绝热过程；

3)环境温度T0=25 ℃，冷藏室温度与蒸发温度的差值为固定值5 ℃。

复叠系统的级间容量比nV为低温回路压缩机进口处制冷剂的体积流量Vl(m3/s)与高温回路压缩机进口处制冷剂的体积流量Vh(m3/s)之比：

(1)

设复叠系统的制冷量Q为200 kW，故低温回路中的制冷剂质量流量ml(kg/s)由式(2)可得：

ml=Q/(h1-h4)

(2)

式中：h1为蒸发器出口(低温回路压缩机入口)状态点的焓值，kJ/kg；h4为蒸发器入口(低温回路膨胀阀出口)状态点的焓值，kJ/kg。

系统中低温及高温回路的压缩机的等熵效率ηs,CO2、ηs,NH3分别为：

(3)

(4)

式中：h2s、h6s分别为绝热压缩时低温回路、高温回路压缩机出口状态点的焓值，kJ/kg；h2、h6分别为实际压缩过程中低温回路、高温回路压缩机出口状态点的焓值，kJ/kg；h5为高温回路压缩机入口状态点的焓值，kJ/kg。

低温回路中压缩机的功耗Wl、高温回路中压缩机的功耗Wh分别为：

(5)

(6)

式中：ηmo,CO2、ηmo,NH3分别为CO2压缩机、NH3压缩机的电机效率，分别取0.9、0.95；ηmec,CO2、ηmec,NH3分别为CO2压缩机、NH3压缩机的机械效率，取0.9；mh为系统高温回路中制冷剂的质量流量，kg/s，可由复叠换热器中两种制冷剂的热交换过程求得：

ml(h3-h2)=mh(h5-h8)

(7)

复叠制冷系统的COP由式(8)可得：

(8)

系统中两回路中制冷剂的体积流量Vl、Vh由式(9)～式(10)得到：

(9)

(10)

式中：ρ1、ρ5分别为低温回路及高温回路压缩机入口处制冷剂的密度，kg/m3。

1.3 数学模型

本文重点研究考虑实际压缩机效率的NH3/CO2复叠制冷系统的最佳中间温度TLC,opt及最优级间容量比nV,opt随工况的变化。以系统蒸发温度改变为例，复叠系统最佳中间温度及最优级间容量比的计算流程如图4所示。给定某一中间温度，取系统蒸发温度为最小值，依次增加0.005 ℃，进行热力分析计算，得到对应的COP，过程中COP最大时对应的中间温度即为该变工况下的系统最佳中间温度，对应的级间容量比即最优级间容量比。

图4 系统性能参数计算流程

2 结果讨论

2.1 压缩机效率分析

压缩机效率直接影响系统性能，当高低温级压缩机的等熵效率均取定值时，复叠制冷系统的COP随蒸发温度的变化如图5所示。其他工况一定时，压缩机等熵效率每增加10%，系统COP增加约16.1%。因此为了保证结论的准确性，热力学分析过程中压缩机效率应贴近实际值。

图5 压缩机等熵效率对系统COP的影响

压缩机等熵效率是压缩机等熵绝热功率与实际轴功率的比值，与压缩机进口与出口的制冷剂状态有关，因此不同制冷剂对应的压缩机等熵效率的经验公式不同[14]。对于NH3/CO2复叠制冷系统，本文作者整理了现有文献中NH3压缩机、CO2压缩机的等熵效率ηs的经验公式[15-17]。

NH3压缩机：

ηs=1-0.04RC

(11)

ηs=0.839 55-0.010 26RC-0.000 97RC2

(12)

CO2压缩机：

ηs=1.003-0.121RC

(13)

ηs=0.934 3-0.044 78RC

(14)

ηs=0.898 10-0.092 38RC+0.004 76RC2

(15)

ηs=-0.456 +1.483RC-0.54RC2+

0.059 3RC3

(16)

式中：RC为压缩机排气压力pdis与吸气压力psuc的比值。

(17)

将上述压缩机等熵效率的经验公式代入复叠制冷系统的系统最佳中间温度的数值计算中，不同压缩机等熵效率的经验公式对中间温度的影响如图6所示。由图6可知，不同等熵效率所得的系统最佳中间温度不同，相同工况下最大差异值为7.53 ℃。

图6 不同压缩机等熵效率的经验公式对中间温度的影响

将上述压缩机等熵效率的经验公式代入复叠制冷系统的COP计算中，并与相同工况条件下实验得到的系统COP进行对比，结果如图7所示。当系统冷凝温度为35 ℃、蒸发温度由-40 ℃增至-30 ℃，NH3和CO2压缩机的等熵效率计算分别采用式(12)与式(15)时，系统COP的数值计算结果与实验结果差值最小，平均误差仅为1.6%，本文数值计算中将采用该组经验公式。

图7 数值计算结果与实验数据的对比

2.2 系统性能分析

利用选定的压缩机等熵效率经验公式，采取图4所示流程，计算分析了NH3/CO2复叠制冷系统性能系数最大值COPmax、最佳中间温度TLC,opt、最优级间容量比nV,opt随多温度工况的变化趋势。

系统蒸发温度Te、冷凝温度Tc、复叠换传温差Td对COPmax、TLC,opt的影响如图8所示。当Te、Td及Tc分别增大时，TLC,opt均随之升高。Te、Td每分别升高5 ℃，TLC,opt分别升高约2.23 ℃、1.88 ℃；Td从2 ℃增至12 ℃，TLC,opt升高约6.16 ℃。COP随Te的升高而提高，随Td及Tc的增大而减小。Te每升高5 ℃，COPmax增加约18.5%；Td从2 ℃增至12 ℃，COPmax降低约20.62%；Tc每升高5 ℃，COPmax随之降低约8.09%。

图8 蒸发温度、冷凝温度、复叠传热温差对系统最大COP、最佳中间温度的影响

Te、Tc、Td对nV,opt的影响如图9所示。nV,opt随Te及Td的增大而减小，随Tc的升高而增大。Te每升高5 ℃，nV,opt减少约3.7%；Td从2 ℃增至12 ℃，nV,opt降低约15.04%；Tc每升高5 ℃，nV,opt增大约6.34%。nV,opt变化是因温度工况改变引起复叠换热器中热平衡移动，使高低温回路中的制冷剂流量及密度改变，致使压缩机的体积流量发生变化。

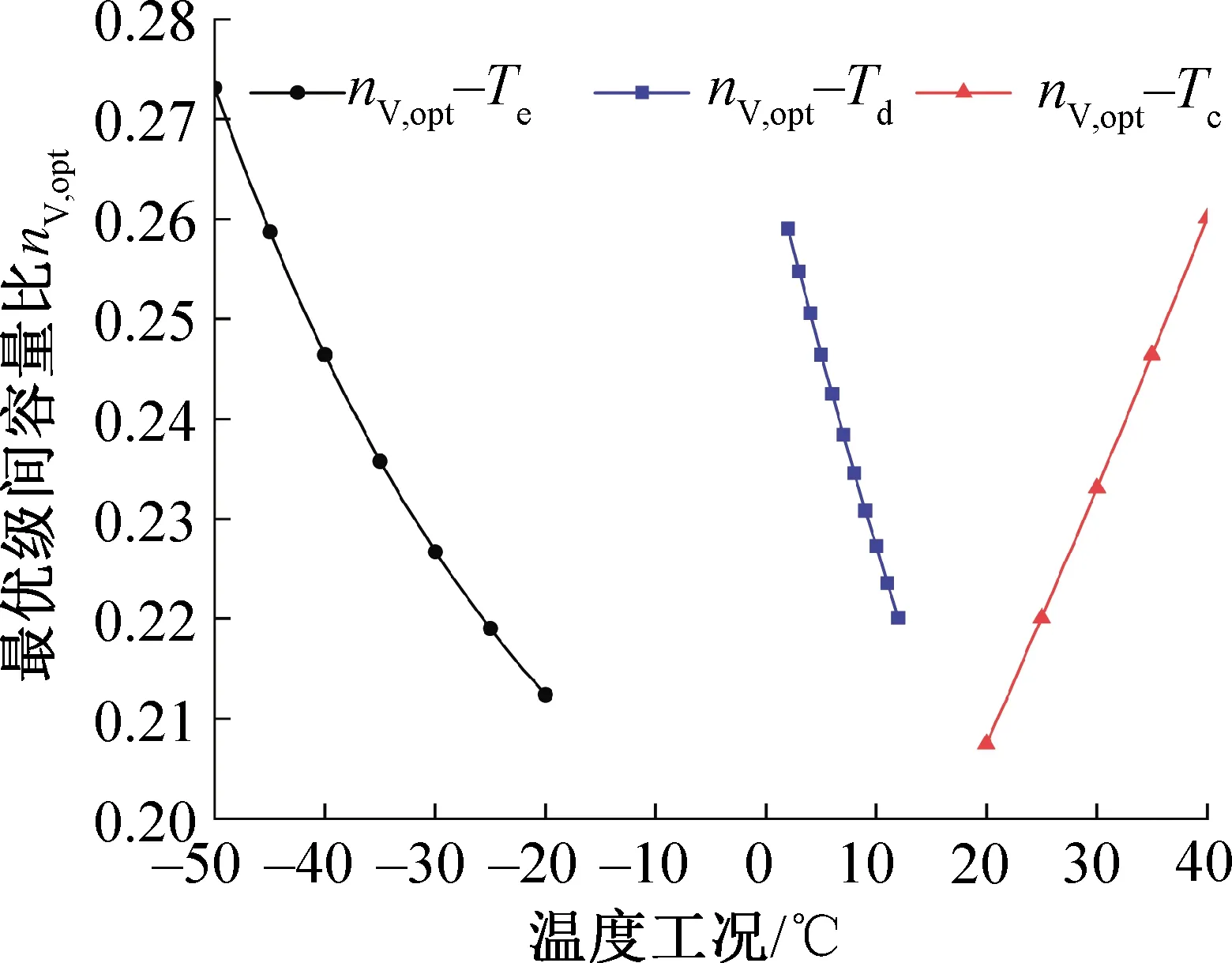
图9 蒸发温度、冷凝温度、复叠传热温差对最优级间容量比的影响

在Te=-40 ℃、Tc=35 ℃、Td=5 ℃时，高低温回路过冷度对系统性能的影响如图10所示。随着过冷度的增加，COPmax随之提高，低温回路过冷度Tlsc每提高2 ℃，COPmax提高1.67%，高温回路过冷度Thsc每提高2 ℃，COPmax提高0.57%。其中，低温回路过冷度的存在对系统性能改善的效果更好。

图10 过冷度对系统最大COP、最佳中间温度、最优级间容量比的影响

Tlsc每增加2 ℃，TLC,opt增加0.16 ℃，nV,opt增加约0.7%；Thsc每增加2 ℃，TLC,opt降低0.12 ℃，nV,opt增加0.38%。nV,opt的变化在于过冷度变化引起回路中单位质量制冷量的变化，影响回路中所需制冷剂的质量流量。单一回路中过冷度的影响造成复叠换热器中平衡的移动，致使体积流量的相应变化，由于高低温回路制冷剂物性的不同，因此高低温回路过冷度变化影响的程度存在差异。

过热度对COPmax、TLC,opt、nV,opt的影响如图11所示。由图11可知，COPmax随过热度增加而降低。压缩机入口处的过热度增加了压缩机功耗，降低了系统性能。低温回路的过热度Tlsh每增加2 ℃，TLC,opt下降0.092 ℃，nV,opt增加0.017%，COPmax则降低约0.9%；高温回路过热度Thsh每增加2 ℃，TLC,opt降低0.11 ℃，nV,opt降低0.43%，COPmax则降低约0.55%。

图11 过热度对系统最大COP、最佳中间温度、最优级间容量比的影响

最佳中间温度随Tlsh的增加而降低，高低温回路中工质的体积流量均增加，且变化幅度相近，因此其比值变化较小，即nV,opt随Tlsh的变化不显著。由于Te和Tc均固定，随着Thsh的增加，中间温度升高，高低温回路中工质的体积流量均增加，且高温回路中工质体积流量增幅更大，因此nV,opt随Thsh的增加而降低。