应对潮汐客流的城市轨道交通列车节能和乘客节时运行图优化模型

冉昕晨，陈绍宽，柏 赟，陈 垚，陈哲轩，杨 晨

（北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044）

客流潮汐现象主要是指因职住分离导致城市轨道交通高峰客流方向分布不均衡的现象，是当前城市轨道交通运营组织关注的重点。高峰客流方向的不均衡性往往导致大客流方向运能紧张，而小客流方向运能富余。运能紧张的方向满载率较高，而运能富余的方向通常存在列车满载率偏低、单位人公里能耗偏高等问题，一定程度上造成了运能与电能的浪费。

为提高运能与需求的匹配程度，国内外既有研究从运营组织层面提出的优化方法可分为3 类：一是灵活设计列车多交路［1−3］、多编组与变编组［4−7］方案；二是组织列车单向加密不对称运行［8−10］；三是组织列车放空运行，即不载客、过站不停车［11］。3类方法中，多交路、多编组与变编组技术侧重于解决客流断面分布和时间分布不均衡场景下的运营组织优化问题，且要求线路具有组织多交路、多编组或变编组的条件［12−13］；不对称运行与放空运行技术侧重于降低客流方向分布不均衡线路的运营成本，但前者要求线路两端均有车辆段或停车场［14］，建设成本较大、车底接续较困难。综合来看，为了在有限的车底资源下维持车底周转，组织部分列车放空运行实施便捷、成本较低，是一种更适合用于应对潮汐客流的节能运行措施。

综合既有研究成果来看，组织列车放空运行的理论研究成果相对较少，但实践中我国深圳地铁4号线已采用放空运行方案，降低了高峰时段约1/3的制动、起动能耗［11］。同时，实践中也发现，组织部分列车放空运行虽能达到节能目的，但会导致部分乘客等待时间增加、非站站停的放空列车与站站停的载客列车追踪距离缩短等问题，仍需在既有研究基础上，结合实际中存在的问题进一步探究计划运行图的优化方法。

为实现客流断面和客流方向分布不均衡特征下的城市轨道交通运行图优化，提出一种考虑大小交路和列车放空运行的列车节能和乘客节时运行图优化模型。首先，结合动态客流需求分析乘客在大小交路和放空运行组织下的上、下车过程；然后，构建以列车总牵引能耗最小化和乘客总等待时间最小化的双目标运行图优化模型，采用非支配排序遗传算法Ⅱ与熵权法相结合的方法进行求解；最后，以具有潮汐客流特征的某条地铁线路为背景，依托实际中的某工作日早高峰计划运行图方案，验证模型适用性及其优化效果。

1 问题描述

某车站总数为N的城市轨道交通线路示意图如图1所示。假设沿车站编号1 至N的方向为上行，反之为下行；车站M具备折返条件，可开行大小交路；车站1—车站M为区域1，车站M—车站N为区域2；车辆段位于线路1 端，与车站1 衔接。为应对断面和方向不均衡的客流，基于该线路的运行图优化要解决的问题是：确定上、下行大小交路站站停载客列车和非站站停放空列车的开行序列，在有限的时空与车底资源下实现列车总牵引能耗和乘客总等待时间的双目标优化。

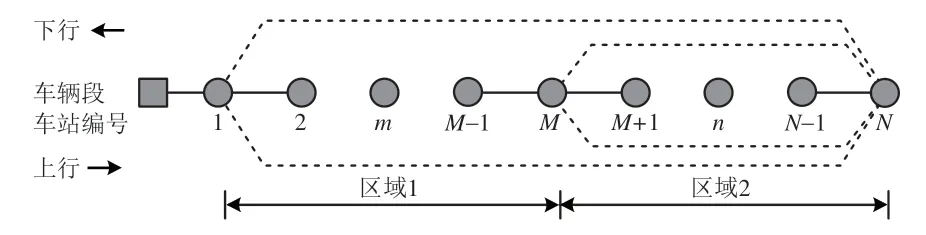
图1 线路示意图

为便于建模，进一步做出如下假设：

（1）不考虑列车越行；

（2）仅考虑线路开行大小交路、且小交路折返位置已知的场景；

（3）向乘客提供服务时遵循“先到先服务”原则，乘客优先选择直达列车；

（4）研究时段内上、下行方向计划发车间隔、区间运行时间、停站时间均为已知常量；

（5）为保证运行秩序，放空列车在线路给定运行时分下选择节能化模式开行。

为便于理解，定义模型主要参数如下：m和n为车站索引；Ns为车站集合，Ns={1，2，…，m，…，n，…，N}；I为上行方向开行列车总数；i为上行列车索引；Iup为上行列车集合，Iup={1，2，…，i，…，I}；J为下行方向开行列车总数；j为下行列车索引；Jdn为下行列车集合，Jdn={1，2，…，j，…，J}；pm，n，t为t时刻起，单位时间内起点车站m—终点车站n的乘客需求，人；和分别为上行列车i和下行列车j经停车站n时的上车乘客数，人；和分别为上行列车i和下行列车j经停车站n时的下车乘客数，人；为上行列车i在车站n—车站（n+1）区间运行时的载客量，人；为下行列车j在车站n—车站（n−1）区间运行时的载客量，人；和分别为上行列车i和下行列车j到达车站n的时刻，s；和分别为上行列车i和下行列车j从车站n出发的时刻，s。

定义模型决策变量为上、下行大小交路站站停载客列车和非站站停放空的列车开行序列：φi和φj分别为确定上行列车i和下行列车j交路类型的0-1变量，大交路时取1，小交路时取0；εi和εj分别为上行列车i和下行列车j是否放空的0-1变量，站站停载客运行时取1，非站站停放空运行时取0。

2 模型构建

乘客上车、乘车和下车过程是计算乘客等待时间与列车牵引能耗的关键要素，且这一过程会受到上、下行列车的交路形式与列车开行序列影响。为此，首先结合自动售检票系统的乘客刷卡数据，推算各站点上、下车乘客数量和各区间载客量；其次建立基于大小交路和列车放空运行的运行图优化模型，以列车总牵引能耗与乘客总等待时间为优化目标，并考虑满足实际运营各项约束条件。

2.1 客流计算

通过乘客刷卡数据，可获线路各时段各OD 对乘客的到达率［15−16］；再结合列车时刻表，可推算得到上、下行列车在某站经停时上、下车的乘客数量和区间运行时的载客量。

1）上车乘客数量

上行列车i经停车站n时，在此站上车的乘客数量为

式中：si，n为0-1 变量，判断列车i是否在车站n停站上、下客，是则取值为1，反之为0；pn，m，t为t时刻起，单位时间内起点车站n—终点车站m的乘客需求，人；和分别为列车i与列车i′在车站n的有效发车时刻，即乘客能够登上列车的最晚到达时刻［17］，晚于有效发车时刻后到达的乘客则等待下1 列列车，s；i′为在车站n停站上、下客的列车集合中，位移大于列车i且距其最近1 列列车的编号。

下行列车j经停车站n时，在此站上车的乘客数量需按图1中区域1与区域2分别计算。

当车站n位于区域1 时，乘客选择乘坐载客的大交路列车，此时为

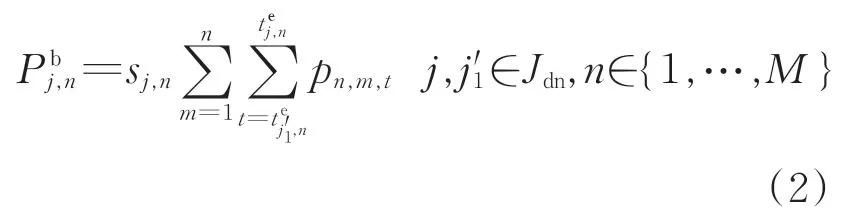
式中：sj，n为0-1 变量，判断列车j是否在车站n停站上、下客，是则取值为1，反之为0；与分别为列车j与列车j′1在车站n的有效发车时刻，s；列车j′1为在区域1 停站上、下客的大交路列车集合中，位移大于列车j且距其最近1列列车的编号。

当车站n位于区域2 时，又可进一步分为车站m位于区域1 与位于区域2 这2 种情况：当车站m位于区域1 时，根据假设（3），乘客选择乘坐载客的大交路列车；当车站m位于区域2 时，乘客可选择乘坐载客的大交路或小交路列车。这2 种情况下在此站上车的乘客数量均为

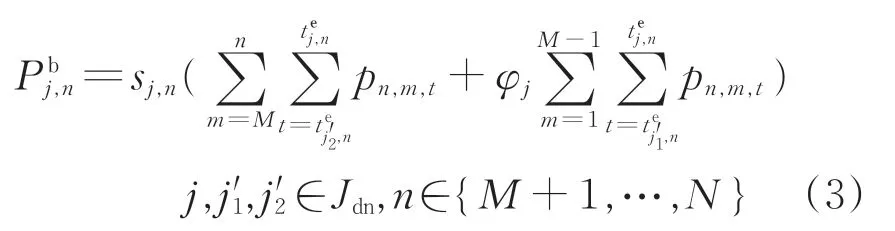
式中：为列车j′2在车站n的有效发车时刻，s；列车j′2为在区域2 停站上、下客的列车集合中，位移大于列车j且距其最近1列列车的编号。

2）下车乘客数量

上行列车i经停车站n时，在此站下车的乘客数量同样需按区域1 和区域2 这2 种情况分别计算。

当车站n位于区域1时

式中：和分别为列车i和i′1在车站m的有效发车时刻，s；i′1为在区域1停站上、下客大交路的列车集合中，位移大于列车i且距其最近1 列列车的编号。

当车站n位于区域2时

式中：为列车i′2在车站m的有效发车时刻，s；i′2为在区域2 停站上、下客的列车集合中位移大于列车i且距其最近1列列车的编号。

下行列车j经停车站n时，在此站下车的乘客数量同样需按区域1 和区域2 这2 种情况分别计算。

当车站n位于区域1时

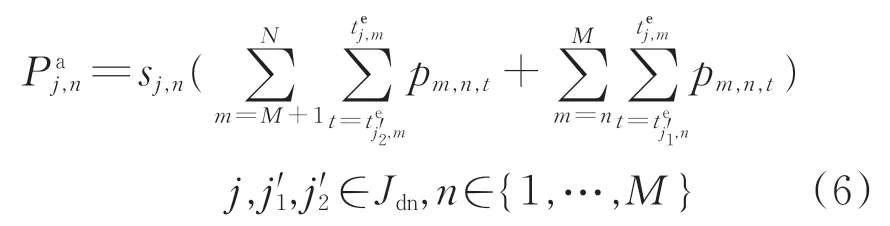
当车站n位于区域2时

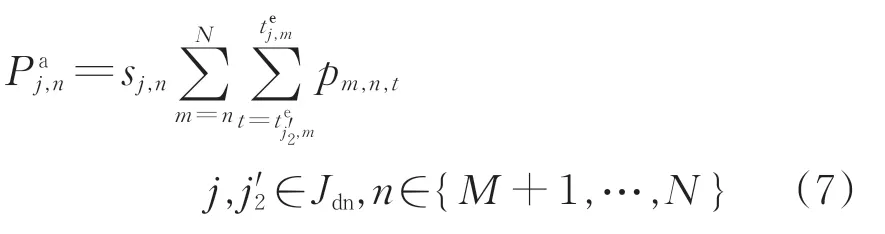
3）列车在区间运行时的载客量

上行列车i在车站n—车站（n+1）区间运行时，载客量为

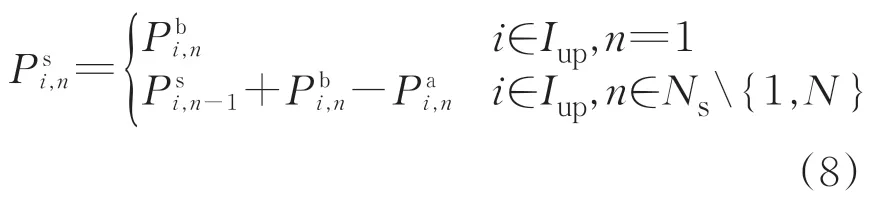
下行列车j在车站n—车站（n−1）区间运行时，载客量为

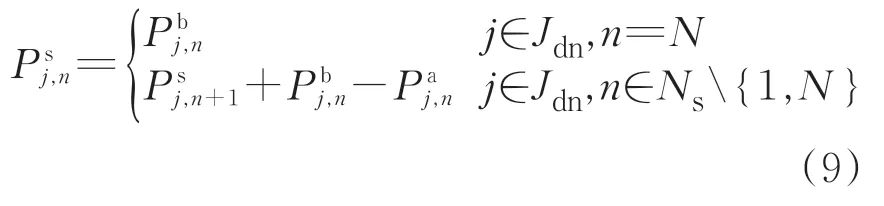
2.2 目标函数

基于有限的时空与车底资源，运行图优化的目标为列车总牵引能耗和乘客总等待时间的双目标最小化。

1）列车总牵引能耗目标

研究时段内，列车总牵引能耗E为上行总牵引能耗Eu和下行总牵引能耗Ed之和，而Eu与Ed又由大小交路列车的牵引能耗组成，即

其中，

式中：ei，n为上行列车i在车站n—车站（n+1）区间运行时的牵引能耗，kW·h；ej，n为下行列车j在车站n—车站（n−1）区间运行时的牵引能耗，kW·h；ei，n和ej，n均可按文献［18］和文献［19］提出的方法，通过牵引计算得到。

2）乘客总等待时间目标

研究时段内，乘客总等待时间Tw包含上行方向乘客总等待时间Tw，u和下行方向区域1 与区域2内的乘客总等待时间和，即

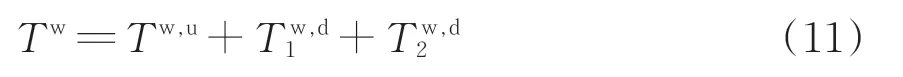
其中，

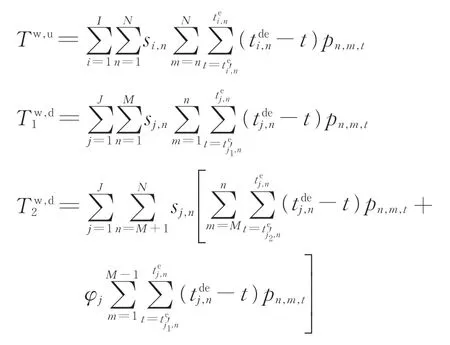
式中：与分别为上行列车i与下行列车j从车站n的出发时刻，s。

2.3 约束条件

模型考虑的约束条件有6 个，包括车底衔接约束、车底规模约束、最小折返时间约束、列车容量约束、最短追踪距离约束和相邻2 列大交路站站停列车间的小交路列车和放空列车数量约束。

1）车底衔接约束

上、下行列车在车站N、车站M和车站1（始发站）这3 个折返站的衔接应满足约束式（12）—式（17）。

式（12）和式（13）用于确保上行列车i与下行列车j在车站N衔接的唯一性。

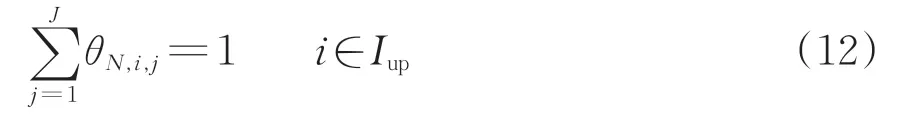
式中：θN，i，j为0-1 变量，上行列车i的车底在车站N折返后，如果继续执行下行列车j的任务则取1；否则取0。

式（14）和式（15）用于确保下行小交路列车j与上行小交路列车i在车站M衔接的唯一性。

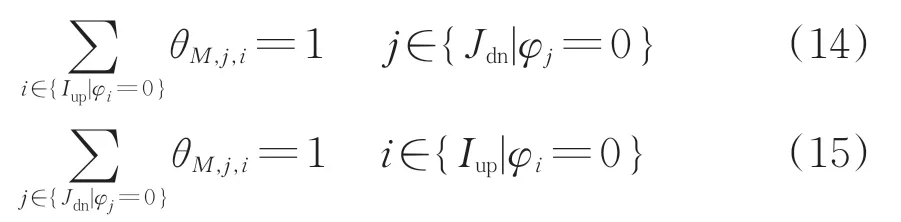
式中：θM，j，i为0-1 变量，下行小交路列车j的车底在车站M折返后，如果继续执行上行小交路列车i的任务则取1；否则取0。

式（16）和式（17）用于确保下行大交路列车j最多只能与1 列上行大交路列车i在车站1 衔接。式（16）取等于表示下行列车j在车站1 折返后，继续上线运行；取小于表示下行列车j下线，返回车辆段。式（17）取等于表示上行列车i由在车站1 折返后的车底执行；取小于表示上行列车i由车辆段发出。

式中：θ1，j，i为0-1 变量，下 行大交路列车j的车底在车站1 折返后，如果执行上行大交路列车i的任务则取1；否则取0。

2）车底规模约束

研究时段内车底总数不应超过车底规模Fmax，即

其中，

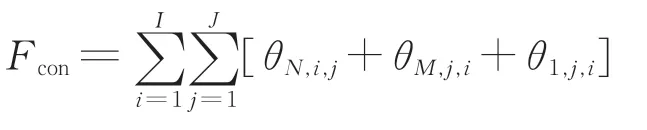
式中：Fcon为在车站N、车站M和车站1 这3 个折返站衔接成功的列车总数，列。

3）最小折返时间约束

折返列车的折返时间不应低于折返站的最小折返时间，应满足约束式（19）—式（21）。

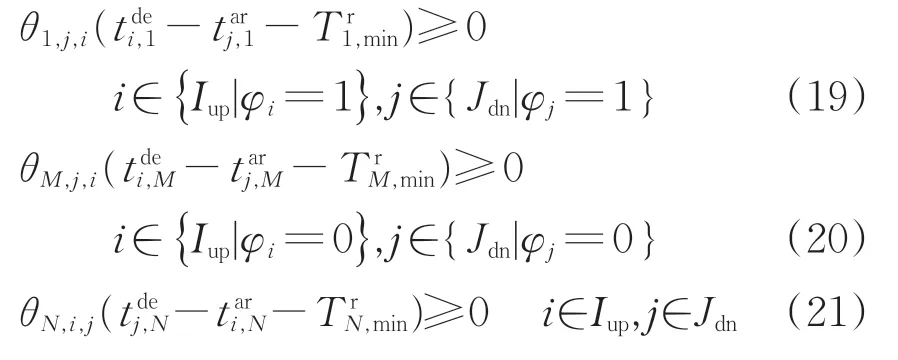
式中：和分别为上行列车i从车站1和车站M的出发时刻，s；和分别为下行列车j到达车站1 和车站M的时刻，s；为 下行 列 车j从车站N的出发时刻，s；为上行列车i到达车站N的时刻，s；，和分别为车站N、车站M和车站1这3个折返站的最小折返时间，s。

4）列车容量约束

上、下行列车在每个区间的载客量应满足约束式（22）和式（23）。

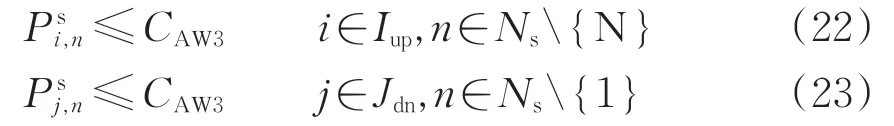
式中：CAW3为列车最大载客量，人。

5）列车最短追踪距离约束

由于放空列车与站站停列车存在技术速度差，运行过程中，相邻2 列列车的追踪距离应满足约束式（24）和式（25）。

式中：vi，t和vj，t为上行列车i和下行列车j在t时刻的速度，m·s−1；β为常用制动减速度，m·s−2；Lt为列车长度，m；Ls为后车车头距前车车尾的最小安全距离，m；i′′为位移大于上行列车i且距其最近1 列列车的编号；δi，i′′，t为0-1 变量，如果上行列车i在t时刻的追踪对象为列车i′则取1，否则取0；Li，i′，t为t时刻上行列车i的中心线与列车i′′中心线的距离，m；j′′，δj，j′′，t和Lj，j′′，t分别与i′′，δi，i′，t和Li，i′，t含义相似，体现下行方向的类似情况。

6）相邻大交路站站停列车间的小交路列车和放空列车数量约束

为保证服务水平，避免乘客因开行小交路列车和放空列车而等待时间过长，上、下行相邻2 列大交路站站停列车间的小交路列车和放空列车的总数应满足约束式（26）和式（27）。

式中：σ为相邻2 列大交路站站停列车间最大允许的小交路列车和放空列车总数，列；i*为上行列车索引，即从列车（i−σ）到列车i范围内的列车编号；j*为下行列车索引，即从列车（j−σ）到列车j范围内的列车编号。

3 算法求解

求解上述双目标非线性优化模型时，非支配排序遗传算法Ⅱ（NSGA-Ⅱ，Non-dominated Sort⁃ing Genetic Algorithm Ⅱ）［20］是一种应用广泛、收敛性较好的求解方法。为获得运行图的满意解，本文采用NSGA-Ⅱ和熵权法［21］相结合的方法，通过NSGA-Ⅱ求解列车总牵引能耗和乘客总等待时间的第一非支配前沿；通过熵权法求解第一非支配前沿解集的客观权重，进而筛选出满意解。

算法求解流程如图2所示。图中：x和X分别为迭代次数索引和最大迭代次数；x′为满意解持续不变的最大代数；Y为种群规模；pc为交叉概率，pm为变异概率。

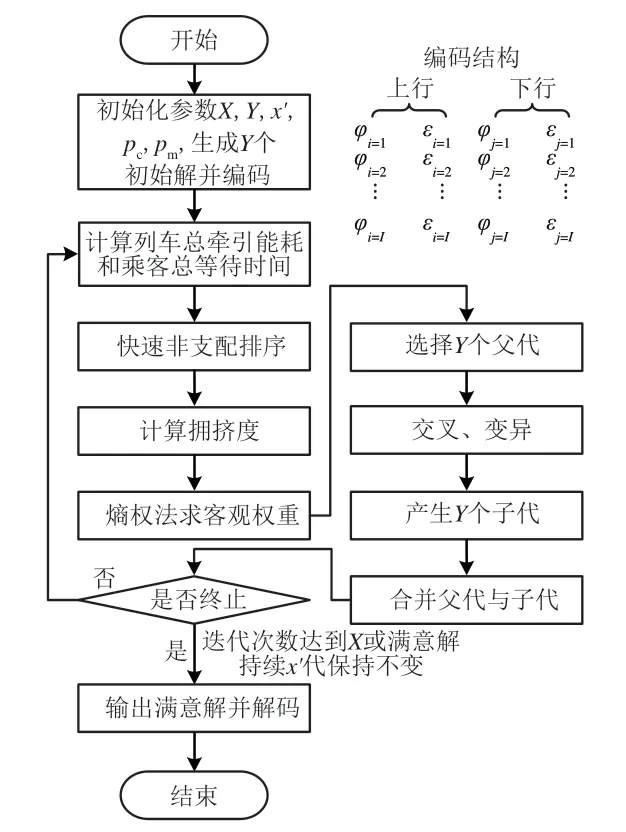
图2 算法流程图

算法的主要步骤如下。

步骤1：生成Y个可行染色体，每个染色体的编码由大小交路和放空列车的0-1 决策变量φi，φj，εi和εj构成。

步骤2：计算种群内每个解的列车总牵引能耗与乘客总等待时间。

步骤3：根据每个解的目标值，对种群进行快速非支配排序和拥挤度计算。

步骤4：采用熵权法对第一非支配前沿解集的双目标进行极差正规化、信息熵计算求得双目标的客观权重，然后选取第一非支配解集上综合加权目标最小的解作为当前代数的满意解。

步骤5：通过二元锦标赛法选择Y个父代，经交叉、变异生成Y个子代，并合并父代与子代。

步骤6：判断是否终止迭代，若迭代次数x达到X或满意解持续x′代保持不变，转入步骤7；否则，返回步骤2继续迭代。

步骤7：终止迭代，输出满意解，并解码生成运行图。

4 案例分析

为验证模型与算法的有效性，选取某市地铁线路A 进行研究。该线路包含12 座车站和1 个车辆段，列车为6B 编组。线路A 在早、晚高峰时段按大小交路组织列车运行，小交路折返站M位于车站8。以2018年4月某工作日的客流数据为基础，以10 min 为统计间隔，对线路A 各时段上、下行方向乘客总进站量进行统计，结果如图3所示。可见，线路A 客流呈现潮汐现象，早、晚高峰客流方向不均衡性明显。

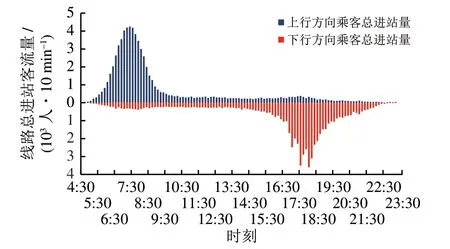
图3 线路A上、下行方向的进站客流时间分布

选取线路A 早高峰时段进行大小交路和放空运行组织下的运行图优化。主要参数设置如下：平均发车间隔时间为3 min，上、下行列车总数I和J均为41 列，车底规模Fmax为22 列，列车最大载客量CAW3为1 880 人，相邻2 列大交路站站停列车间最大允许的小交路列车和放空列车总数σ为1 列。上、下行列车计划停站时间与区间运行时间分别见表1和表2。表中放空列车在所有中间站不停站通过，且旅行速度与其同方向、同交路的站站停载客列车一致。

表1 上行列车计划停站时间与区间运行时间

表2 下行列车计划停站时间与区间运行时间

4.1 运行图优化效果验证

为验证运行图优化模型的列车节能与乘客节时效果，利用NSGA-Ⅱ和熵权法对模型进行优化，并通过运行图对比优化方案与实际方案、单一大交路站站停方案（不开行小交路且不允许列车放空）在列车总牵引能耗和乘客总等待时间等方面的差异。

实际运行图采用某工作日的真实早高峰计划运行图方案，早高峰大小交路比例为1∶1 且下行方向（小客流方向）所有小交路列车放空运行，如图4所示。

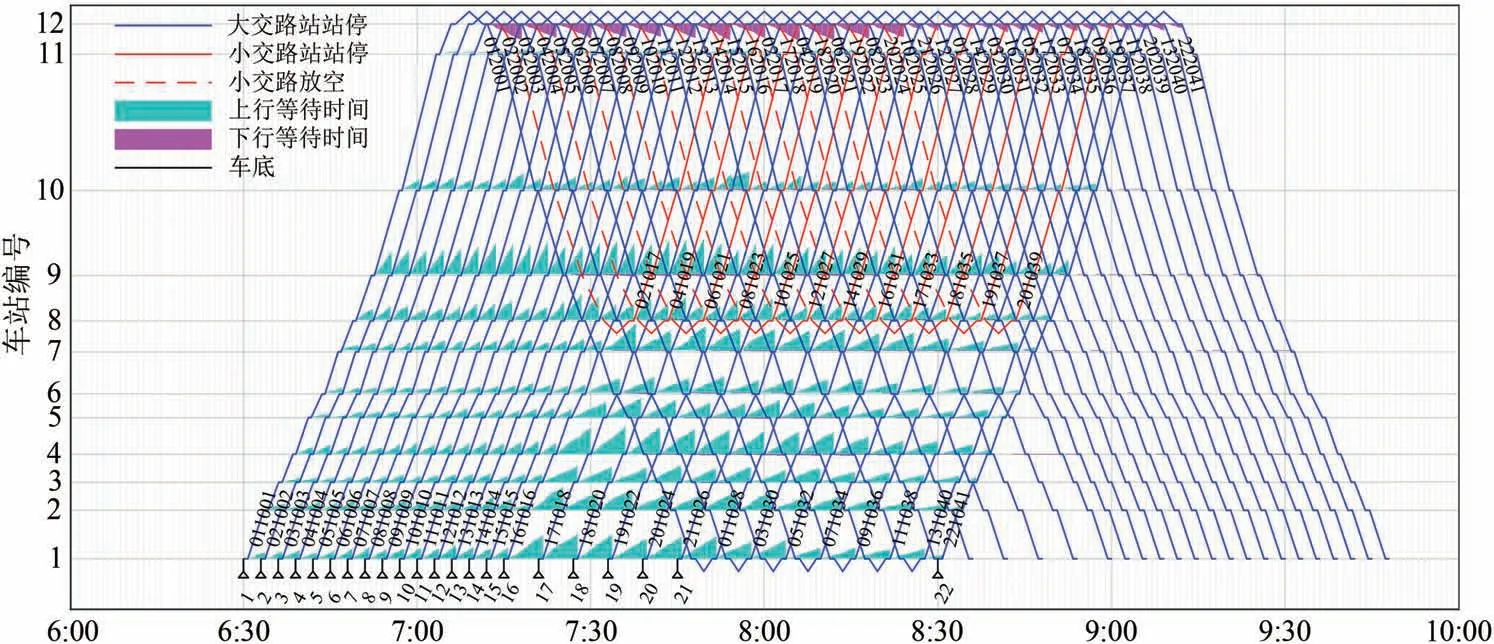
图4 实际运行图

设算法种群规模为100 个，最大迭代次数为500次，满意解持续保持不变的最大代数为100代，交叉概率为0.9，变异概率为0.1。列车总牵引能耗和乘客总等待时间的收敛过程如图5所示。随着迭代次数的增加，列车总牵引能耗波动下降、乘客总等待时间波动上升，在第66 代后开始收敛，列车总牵引能耗稳定为11 497 kW·h，乘客总等待时间稳定为1 462 h。

图5 算法收敛过程

算法收敛后，模型优化满意解方案为归一化加权总目标值最小的方案，对其解码后的优化运行图如图6所示。对比图4和图6可看出，优化方案将图4中上行小交路列车021017和141029调整为图6中上行大交路列车171017 和021029，使在列车161016—181018、列车011028—031030 之间到达车站1—车站8 的乘客总等待时间减少；但同时优化方案增加了830 以后时段下行大交路放空列车的数量，使列车222026—142041 之间到达乘客的总等待时间增加。

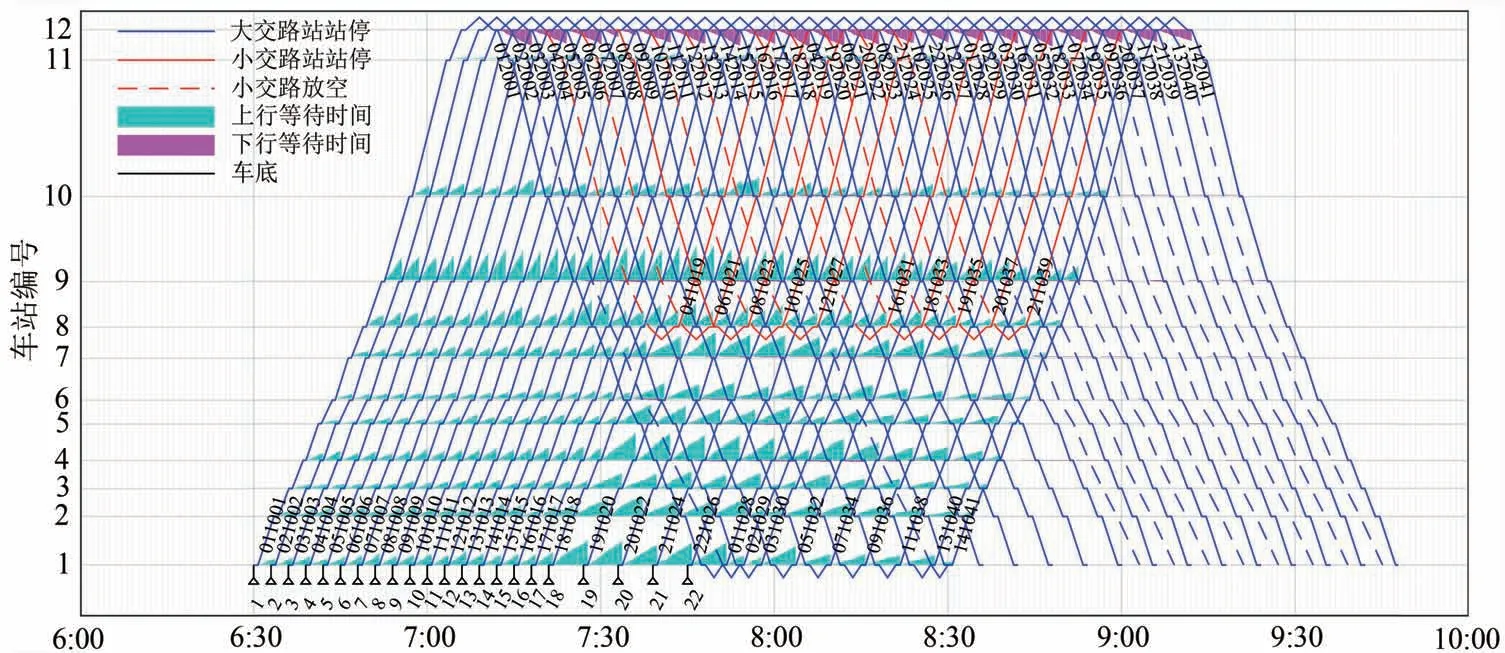
图6 优化运行图

列车总牵引能耗和乘客总等待时间的第一非支配前沿与归一化加权总目标如图7所示。经熵权法计算，列车总牵引能耗和乘客总等待时间的客观权重分别为0.499 3 和0.500 7。图7表明：乘客总等待时间随列车总牵引能耗增加而降低；仅追求列车总牵引能耗最小化的方案结果为11 276 kW·h 和1 528 h，相比于实际方案可实现3.60%的列车节能，但同时会增加2.00%的乘客总等待时间；仅追求乘客总等待时间最小化的方案结果为12 062 kW·h 和1 413 h，相比于实际方案可实现5.67%的乘客节时效果，但同时会增加3.12%的列车总牵引能耗；而通过熵权法筛选出的优化方案结果为11 497 kW·h 和1 462 h，相比于实际方案能同时实现与1.71%的列车节能和2.40%的乘客节时，实现了二者的共同优化。

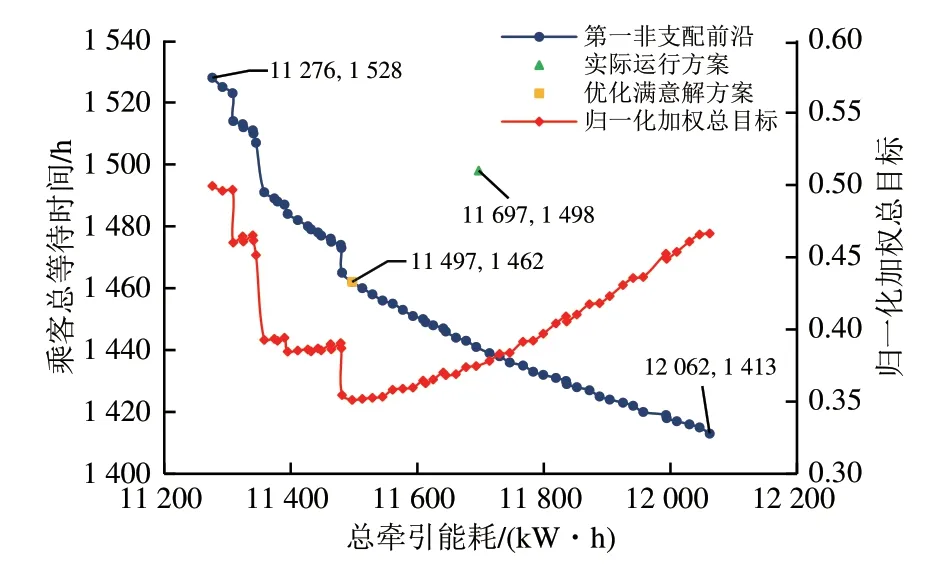
图7 算法优化结果

进一步地，分上、下行方向分别对比3 种方案的运行图指标见表3。

由表3对比优化方案与单一大交路站站停方案可知：组织大小交路和列车放空运行不仅有利于节能，还能减少车底数量，节省企业的运营成本与车辆购置成本。

由表3对比优化方案和实际方案可知：2 种方案在不同方向的列车节能和乘客节时效果存在差异；在列车节能效果方面，优化方案通过增加图6中8：30 以后时段下行大交路放空列车的数量，降低了列车总牵引能耗的6.09%，但放空下行大交路列车使图6中列车222026—142041 之间到达乘客的总等待时间增加了16.67%；在乘客节时效果方面，优化方案以增加上行大客流方向2.29%的列车总牵引能耗为代价，降低了大客流方向4.69%的乘客总等待时间；虽然早高峰时段组织开行的下行大交路放空列车增加了部分乘客的等待时间，但由于下行总客运量较小，仅为上行的1/11，总体上仍是节时的；早高峰时段留乘总人数降低了26.62%，总体上满载率均衡性得到提高。

表3 实际方案与单一大交路站站停方案、优化方案的指标对比

综上所述，相比于单一大交路站站停方案，优化方案减少了车底数量；相比于实际方案，优化方案在不增加车底数的前提下在上行大客流方向实现了乘客节时，在下行小客流方向实现了列车节能，总体上实现了列车总牵引能耗和乘客总等待时间的共同优化。

4.2 灵敏度分析

优化模型中，相邻2 列大交路站站停列车间最大允许的小交路列车和放空列车之和σ是影响解空间大小，并由此成为影响运行图列车总牵引能耗与乘客总等待时间的重要参数。在其余条件均不变的前提下，通过仅调整σ取值的形式优化运行图。当σ>4时，部分乘客等待时间将超过15 min，不符合实际。因此分别考虑σ=1，2，3和4时，优化运行图的列车总牵引能耗和乘客总等待时间的变化趋势，结果如图8所示。

图8表明：随着σ的逐步递增，列车总牵引能耗递减，而乘客总等待时间递增；以σ=1 为对比组，当σ分别取2，3 和4 时，列车总牵引能耗分别降低了2.13%，7.84%和8.29%，而乘客总等待时间分别增加了3.42%，21.61%和24.08%，特别是当σ从2增至3时，2个目标的取值均发生了明显变化，这是因为σ增加后，大交路区段站站停列车的发车间隔将被延长，导致乘客等待时间大幅增加。因此，在考虑组织大小交路和放空运行时，不宜将σ设置过大，在本案例平均发车间隔为3 min的早高峰时段，σ不宜超过2。

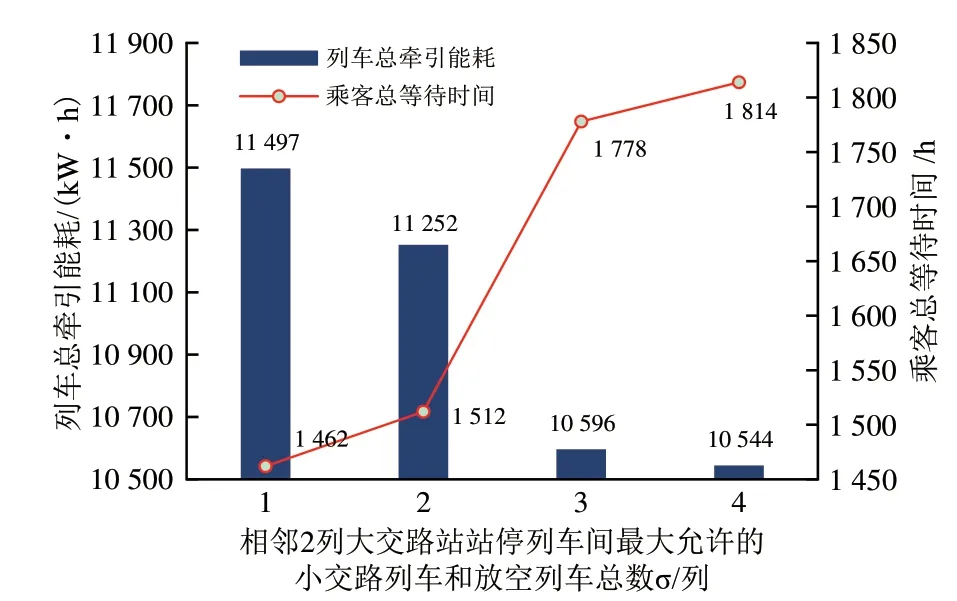
图8 列车总牵引能耗和乘客总等待时间随σ的变化情况

5 结 语

针对城市轨道交通客流断面和客流方向不均衡的线路，结合客流时空动态变化，综合考虑车底衔接、车底规模、列车容量、安全间隔以及相邻2 列大交路站站停列车间小交路列车和放空列车数量等实际约束，提出了一种考虑大小交路和列车放空运行的列车节能和乘客节时运行图优化模型，并以某市具有潮汐客流特征的某地铁线路为背景，依托实际中的某工作日早高峰计划运行图方案，验证了模型的适用性及优化效果。结果表明：优化后的运行图通过组织列车开行大小交路和放空运行，在不影响车底总数的前提下降低了大客流方向乘客总等待时间和小客流方向列车总牵引能耗，在实际运行图的基础上进一步实现了1.71% 的列车节能和2.40%的乘客节时。此外，为了在节能节时的同时保证一定的服务水平，实际运营中应合理控制相邻2 列站站停大交路列车之间小交路列车与放空列车的数量。

本文从牵引能耗指标角度考虑了运行图的耗能情况，但未考虑再生制动能在多列车之间的传递过程。下一步可考虑多列车间能量的协同，实现牵引能耗与再生制动能的协同优化。此外，本文考虑了大小交路下的运行图优化问题，今后可将深入分析多交路下乘客的路径选择，丰富运行图优化模型的适用场景。