考虑灵活存车和列位占用的动车所调车作业计划编制

史锦堂，黎浩东，曹 恒，郑亚晶

（1.北京交通大学 交通运输学院，北京 100044；2.北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044；3.陕西交通职业技术学院 轨道交通学院，陕西 西安 710018；4.华南理工大学 土木与交通学院，广东 广州 510640）

动车运用所（动车所）的调车作业计划决定了所内动车组各项作业先后顺序、占用股道（列位）和占用起讫时刻，是动车所日常生产组织的重要基础计划。随着我国高速铁路的蓬勃发展，部分动车所的检修能力已经接近饱和，逐渐成为制约高速铁路运输系统能力的重要因素之一。在既有设施设备条件下，提升动车所日常调车作业计划的编制质量，对提高其检修能力和设施设备利用水平都具有很重要的现实意义。

国内外部分学者对动车所调车作业问题进行了研究。文献［1］构造了三阶段的时空网络图来表示列车检修车间的调车作业过程。文献［2］设计了股道连通图来揭示股道之间的连通关系，并以减少关键线区总占用时间和调车路径费用为优化目标，建立了包含动车所所有作业的调车作业计划模型。文献［3］以已知动车组占用存车线时间为前提，以提高存车线利用率和减少调车作业走行距离为优化目标，建立了动车所存车线运用的0-1 规划优化模型。文献［4］以提高动车所股道利用率为目标，对尽端式和通过式车场进行研究，建立了车场股道占用优化模型。文献［5］以动车组在动车所内的总延误时间最少为目标，在考虑动车组执行各项作业的工序不定约束基础上，建立了动车所调车作业计划优化模型。文献［6］考虑动车所作业线双列位的因素，以最后1 列动车组检修完成时间最少为目标，建立了动车所一级修作业计划优化模型。文献［7］综合考虑了列位占用和尽端、通过式股道占用时间先后的区别，构建了0-1 整数线性规划模型。文献［8］以动车组车底出入所时间为联系，将动车所内部调车作业计划与外部的高速铁路枢纽站技术作业计划协同编制。文献［9］针对横列、尽端式车场布局的动车所，构建了一级修调车作业整数规划模型。文献［10］在文献［9］的基础上进一步考虑了股道双列位因素。文献［11］综合考虑了包含列车检修、单元重组、股道占用和进路排列的调车计划问题，构建了混合整数规划模型，并用CPLEX 求解。文献［12］针对动车所一级修作业问题，重点考虑了检修与清洗的灵活工序和列位占用，构建了一级修作业的非线性模型，并设计遗传算法来求解。文献［13］建立了考虑列位占用的动车所调车作业计划编制模型，设计了基于启发式规则的模拟退火算法求解模型，并在算法中考虑了短编动车组在动车所内的重联解编作业。文献［14］设计了邻域搜索算法来解决荷兰铁路中的列车单元调车问题。文献［15—16］基于不同视角对动车所的检修能力进行了研究。

国外的相关研究着重考虑了列车单元重组约束，不适用于我国。已有国内的相关研究大多基于假设对实际生产作业进行简化，如假设动车组只需检修与清洗等少数作业［5−6，9−10，12］、所有动车组的检修任务相同［5−7，9−10，12］、所有动车组的检修工序已知［2，6，9，13］、检修时不需要考虑列位占用［2，5，8−9］等。这些假设虽然有利于问题的建模和求解，但也在一定程度上背离了现场实际，降低了提出方法的适用性与通用性，难以应用于实际工作中。特别是当动车所的检修能力不够时，如果不考虑多次灵活存车的操作形式，将会大大增加动车组在检修线上的停留时间，降低计划的抗扰动能力［17］。此外，每条股道均设置了双列位，这也会进一步增加对长、短不同编组列车统一进行调车作业计划编制的难度。

以适用于不同车场布置类型的动车所为前提，本文重点考虑灵活存车、列位占用问题，在统筹各项检修作业先后顺序安排、进路冲突、车场布置类型等现实情况的基础上，建立可用于动车所调车作业计划优化的字典排序目标规划二级模型；以动车所内的所有待开展作业为模型主要索引，通过决策所有作业的股道占用情况，得出所有待检修动车组的调车作业计划；依托某纵列式二级二场布置的动车所设计算例，验证模型的正确性以及其统筹调度所内作业任务的能力。

1 问题描述

目前，我国铁路最常见的动车所布置形式为纵列式二级二场和横列、尽端式，这2 种动车所的具体布置形式如图1所示。图中：罗马数字为咽喉编号；带圈阿拉伯数字为车场中的不同列位位置。根据百度地图的卫星图数据统计，全路54 个动车所中，以这2种布置形式为主体的动车所占85%，且其中过半采用作业间衔接更为顺畅的纵列式布置，即纵列式二级二场布置是我国动车所最典型的布置形式。为适应不同编组动车组的检修作业，动车所内的股道大都设计为2 个列位，这样1 条股道可容纳1列长编动车组或者2 列短编动车组，如图1中，位置①和②分别为通过式车场中靠近Ⅰ和Ⅱ号咽喉的列位集合；位置③和⑤分别为尽端式车场中靠近进口位置的列位集合；位置④和⑥分别为尽端式车场中靠近尽端位置的列位集合。

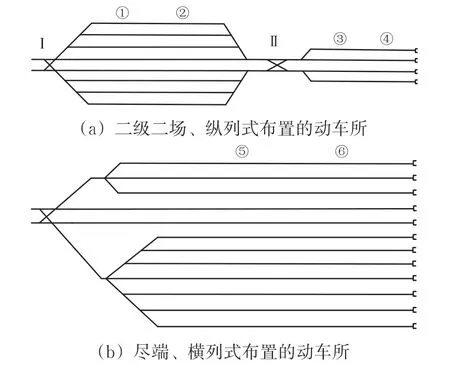
图1 典型的动车所布置形式

动车所内动车组的检修作业内容主要包括：一级修、二级修、吸污作业、清洗作业、探伤作业、车轮镟修作业等，其中二级修又根据动车组的行驶时间和里程分不同等级的检修包来执行。为了开展上述作业，动车所设置了不同功能的车场（线区），如检修场、清洗场、吸污场和存车场等；根据2 端是否都能通行列车，车场又可分为通过式、尽端式等形式。相互连接的车场组成了带有检修、存车等功能的动车所，而不同功能、不同形式车场间的不同连接方式，又形成了不同的动车所布置形式。

动车所日常调车作业计划编制需在给定动车组运用计划（动车组入所、出所时刻）、检修计划和动车所布局及股道数量的前提下，解决检修作业顺序、股道与列位占用和进路冲突疏解等3 个方面的问题，确保所有动车组都能及时完成检修任务，并力求在关键线区总占用时长和总存车次数上达到最小化。

1）灵活存车思路下的检修作业顺序安排

动车组入所检修，必然要在从入所到出所的时间段内，按照一定的作业顺序完成既定的作业任务，而这也是动车所日常调车作业计划需首先确定的问题。将检修、清洗等作业视为必要作业，将存车作业视为非必要作业，某列动车组从入所到出所的各项作业流程如图2所示。图中：实线方框表示必要作业；虚线和点划线方框表示非必要作业；五角星表示作业项目中可能有更多的必要作业及其前序存车作业，在此省略；箭头表示不同作业间转场形成的调车运行进路，包括入所进路、出所进路和作业间的调车进路等。

图2 动车组检修作业流程

动车组入所后，假如此时某项必要作业的作业设备处于空闲状态，将立即进行作业；否则需要在存车场中等待，直至该设备空闲。当动车组某项必要作业结束之后，假如下一项必要作业的作业设备处于空闲状态，将立即进行作业；否则需要在存车场中等待，直至设备空闲。假如动车组下一项必要作业的作业设备及相应存车场设备均处于忙碌状态，则意味着动车组需停留在当前作业的股道上，等待资源释放。动车组完成所有必要作业后，假如存车场中有空闲位置，将进入存车线中等待出发；否则将继续停留在当前作业线上，直至规定的出发时刻或存车场中出现空闲。

以带有一级修和清洗这2 项必要作业的作业任务为例，分析其具体流程。若某待检动车组有这2项必要作业待开展，那么根据设备是否处于空闲状态，存车次数可能为0～3 次，执行进路次数可能为3～6 次，则该动车组从入所到出所，所有可能的作业流程共有以下2×23=16种。

（1）流程1和流程2：到达→一级修/清洗→清洗/一级修→出发。

（2）流程3和流程4：到达→一级修/清洗→清洗/一级修→存车→出发。

（3）流程5 和流程6：到达→存车→一级修/清洗→清洗/一级修→出发。

（4）流程7 和流程8：到达→一级修/清洗→存车→清洗/一级修→出发。

（5）流程9 和流程10：到达→一级修/清洗→存车→清洗/一级修→存车→出发。

（6）流程11和流程12：到达→存车→一级修/清洗→存车→清洗/一级修→出发。

（7）流程13和流程14：到达→存车→一级修/清洗→清洗/一级修→存车→出发。

（8）流程15和流程16：到达→存车→一级修/清洗→存车→清洗/一级修→存车→出发。

综合考虑动车所内的所有作业，部分动车组的必要作业数量不止2 项。若某待检修动车组待开展的必要作业为n项，根据设备是否处于空闲状态，存车次数可能为0～(n+1)次，进路执行次数可能为(n+1)～(2n+2)次，则该动车组从入所到出所，所有可能的作业流程共有n！×2n+1种。

由上述分析可知，当必要作业次数增多时，所有可能的作业流程数量将呈指数级增多，问题的不确定性和复杂性也随之大大提高。以上文一级修为例，虽然必要作业顺序只有2 种（先检修和先清洗），但是考虑了灵活存车之后的所有可能作业流程却有16 种之多。此外，相对于必要作业，增加存车等非必要环节会提高调车作业量，增加咽喉压力，影响动车所能力利用。因此，在动车所日常调车作业计划编制过程中，需尽可能减少动车组的存车次数以及相应的调车作业。

2）股道占用与列位占用

股道占用针对所有动车组，列位占用针对短编动车组。当2 列待检短编动车组同时占用同一股道时，根据车场的布置形式，对动车组的进出又有不同调度规则。假如当前车场为尽端式时，则先进入股道的动车组需要等后进入的动车组离开后才能离开（“先进后出”规则）；当前车场为通过式时，则后进入股道的动车组需要等先进入的动车组离开后才能离开（“先进先出”规则）；当前车场为尽端式与通过式混合连接的形式时，则还需要结合实际情况按规则进行调度。因此，在动车所日常调车作业计划编制过程中，需根据不同车场布局形式，决策短编动车组对具体列位的占用关系。

3）进路冲突疏解

在股道联通关系上，横列、尽端式布置［5，9−10］的动车所股道联通都只能通过唯一的咽喉，相对简单；而纵列式二级二场布置涉及2 个车场的连接，股道联通关系较为复杂，调车路径也更为复杂。假设纵列式二级二场布置的动车所内设有足够的中转线，能够保证动车组在需要转线时都能够顺利转线（尽端式股道在尽端处的列位除外，即图1中位置④和⑥的列位）。例如图1（a）中，中转线设在通过式车场内的某条股道，中转线的两头连接两端的Ⅰ和Ⅱ号咽喉，假设某动车组停在位置①的列位上等待转线到位置③，若位置②有车停留而阻挡转线，动车组可以按Ⅰ号咽喉→中转线→Ⅱ号咽喉的路径到达位置③；否则可以按位置②→Ⅱ号咽喉的路径直接到达位置③。

可行的调车作业计划需要严格避免进路冲突，即2 条敌对进路的执行时间不能交叉重叠。为简化模型中对调车进路冲突的检查与疏解，本文假设同一时刻至多只能执行1条进路［10］，即相邻2次执行进路的中间间隔时间必须大于某个特定的安全间隔时间，通过留足准备时间的形式确保调车作业过程安全。

2 模型构建策略

为使构建得到的模型能够实现多目标下的顺序优化，避免设置单一目标带来的局限性，且动车组检修任务不同的情况下模型能够统筹调度动车所内所有作业任务，需考虑以下2 个因素，分别是多目标下的模型分级处理能力和动车组检修任务不同时的建模对象异质性影响。

1）多目标下模型的分级处理能力

动车所内开展检修、洗车、镟修等作业的股道数量较少，成为制约检修能力的瓶颈，而存车股道资源一般较为丰富，所以动车组结束关键线区的作业后，应尽快腾空当前股道，进入存车场中等待。此外，存车作业为非必要作业，存车次数越少，必要作业之间转线越顺畅，调车作业量和动车所咽喉区时间占用也相应越少，即减少存车次数有利于降低调车成本、提高动车所检修能力利用率，使动车所能够容纳更多的动车组开展检修作业。基于文献［2］，考虑以最小化关键线区总占用时间和最小化总存车次数共同作为目标，但一般情况下减少关键线区总占用时间反而会增加存车线区停留时间，导致总存车次数增加，因此这2个目标互斥。

区别于将不同的目标函数进行线性加权转化为单目标的处理方式，字典排序目标规划（Lexico⁃graphic Goal Programming）［18−19］模型在求解多目标问题时，为各目标函数赋予相应优先级［20］，在顺序求解过程的第一阶段，优先级最高的目标是唯一目标，接下来的阶段，再将下一级的目标作为唯一的目标，以此类推。由此，考虑基于目标规划理论，建立字典排序目标规划模型，结合对2 个目标的分析，分别确立第一优先级和第二优先级。

2）动车组检修任务不同时的建模对象异质性影响

动车所内，不同动车组所需的检修作业互有差异，部分动车组需要进行日常的一级修检修作业，部分动车组需要进行二级修，还有部分动车组只需在存车线上停留而无须进行检修。如果采用动车组作为构建模型的主要索引，往往会引发所有动车组待检作业项目均相同的假设，难以决策出每列动车组在动车所内的股道占用情况。区别于这种构模方式，本文以动车所内的所有待开展作业为构建模型的主要索引，通过决策所有作业的股道占用情况，最终得出每列动车组的调车作业计划。

3 数学模型

根据模型构建策略，围绕动车所内的所有待开展作业设计决策变量，在分析不同子问题的基础上形成模型约束条件，以最小化关键线区总占用时间为第一优先级目标，以最小化总存车次数为第二优先级目标，构建目标规划模型。

3.1 参数和变量定义

在某调车作业计划期内，定义如下集合与索引：O为动车所内所有作业的集合，O={1，2，…，n，n+1，…，2n，2n+1，…，2n+m}，n为所有待检修动车组待开展的所有必要作业数量，m为所有待检动车组的数量，p与q为集合O的索引；A为动车所内所有必要作业的集合，A={1，2，…，n}，A⊂O；I为动车组集合，i为集合I的索引；Il为长编动车组集合，Il⊂I；Hj为作业类j的作业股道集合，包括检修线集合、清洗线集合、吸污线集合和存车线集合等，h为集合Hj的索引；k为股道占用无冲突情形的索引，k∈{1，2，3}。

集合O中，第1～n项表示所有待检修动车组待开展的所有必要作业，即图2中的实线方框；第(n+1)～2n项表示所有必要作业对应的前序存车作业，即图2中的虚线方框（若某必要作业之前无存车作业，则按照存车作业时间为0 计算；若忽略转线时间，则某存车作业的结束时刻是对应必要作业的开始时刻）；第(2n+1)～(2n+m)项表示所有动车组出所前可能会进行的存车作业，即图2中的点划线方框（同样，若进行完必要作业后直接离开，按照最后1 项存车作业时间为0 计算）。如此，编制动车所日常调车作业计划时，可以在寻求目标最优的同时灵活分配每辆动车组存车作业的次数、次序和每次存车作业的时长，达到“灵活存车”的目的。

考虑2 列动车组对同一股道的占用关系，股道占用无冲突的情形共有3 种。以作业p比作业q先占用股道为例，这3 种情形如图3所示。图中：tarp和tdpp分别为作业p所属的动车组进入和离开作业股道的时刻，是模型的决策变量。

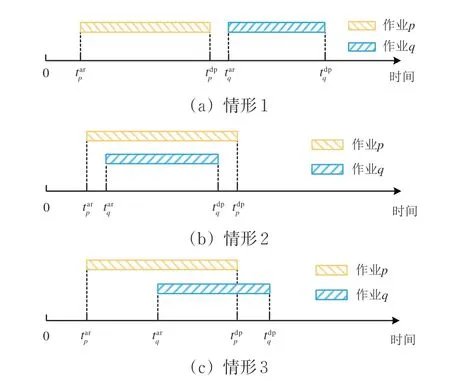
图3 作业p比作业q先占用股道且占用无冲突的3种情形

由图3可知：情形1 中2 项作业占用时间没有重叠；情形2 和情形3 分别表示2 列不同的短编动车组同时占用同一股道2 个列位的情形，且2 项作业的股道占用时间存在重叠；情形2 中作业p先进后出，但这只有在作业p与作业q所属动车组均为短编且占用股道属于尽端式车场时才会出现；情形3中作业p先进先出，但这只有在作业p与作业q所属的动车组都为短编并且占用股道属于通过式车场时才会出现。

基于对这3 种情形的分析，进一步定义如下模型参数：tai与tdi分别为动车组i的入所时刻与出所时刻；gp为作业归属动车组参数，其值等于作业p所属的某动车组的索引；rp为作业归属作业类参数，其值等于作业p所属的某作业类的索引；tmin为按标准完成作业p所需要的最少时间，存车作业所需的最少时间取0；φj为布尔参数，作业类j的作业线区为通过式布置时取1，为尽端式布置时取0；Δt为在同一咽喉前后相邻执行的2 条进路的安全间隔时间或者2 列动车组先后占用同一股道的安全间隔时间；M为1个足够大的正数，在本模型中取本次计划期的时间长度。

除了和外，再定义如下决策变量：xph为布尔变量，作业p在股道h上作业时取1，否则取0；为布尔变量，作业p比作业q先占用同一股道且无冲突时其值取1，否则取0；u+p和分别为实际作业时长与标准作业时间之间的正偏差与负偏差量，均为正整数；v+p和分别为存车次数与0（不存车）之间的正偏差与负偏差量，均为布尔值。

3.2 模型建立

3.2.1 第一优先级模型

按照字典排序目标规划根据目标优先级来顺序求解的理论，第一优先级模型的目标是最小化关键线区总占用时间，即目标函数Z1为最小化实际作业时间与标准作业时间之间的正偏差量。

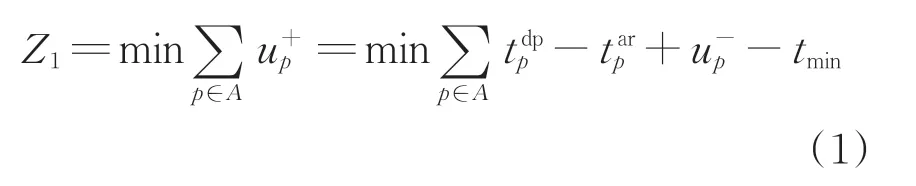
该模型的约束条件有6 个，分别是进出动车所时间约束、作业时间标准约束、动车组作业时间约束、占用车场约束、进路冲突约束和列位占用约束。为简便表示约束，若无特殊标注，均认为动车组与作业的作用范围为集合的全部，即在约束条件中省略∀i∈I，∀p∈O。

1）进出动车所时间约束

此时需同时满足以下3种情况。

最后1项存车作业的结束时刻为离所时刻，即

第1项存车作业的开始时刻为到所时刻，即

所有作业的作业时间总和等于动车组在动车所停留时间段，即

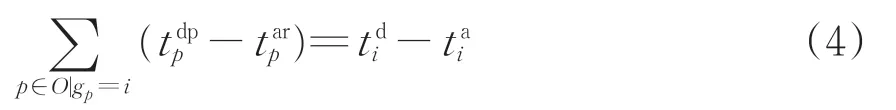
2）作业时间标准约束

此时实际作业时长应不小于相应的最低作业时间标准，即

存车作业的作业时间标准通常设为0，但若存在某些动车组只进行存车过夜、不进行检修清洗的情况，也可以将这些存车作业的时间标准设为其他值。

3）动车组的作业时间约束

假设将转线时间并入作业时间内［5，7］，即相邻2 项作业之间没有时间间隔，那么此时需同时满足以下3种情况。

必要作业的开始时刻等于前序存车作业的结束时刻，即

最后1 项必要作业的结束时刻是最后1 项存车作业的开始时刻，即

同一动车组的任意2 项作业的时间段无重叠，即

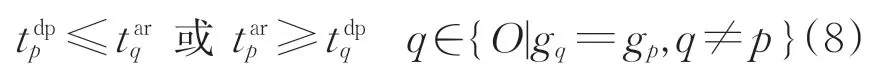
4）占用车场约束

此时动车组仅停留在某1 条属于当前作业线区的股道上，而不会停留在不属于当前作业线区的股道，即

5）进路冲突约束

当某动车组的第1 项作业开始或任意1 项作业结束时，必然会产生调车作业进路，不同动车组的作业之间可能会发生进路冲突，因此还需要保证相邻2 次调车作业之间留有安全时间间隔，避免进路冲突的发生，即

6）列位占用约束

首先，同一时刻占用同一股道的动车组不会超过2列，即

需要注意的是，前述股道占用的3 种情形是基于作业p比作业q先占用股道的设定，事实上，作业q有可能比作业p先占用股道，因此同理可知，另有3 种股道占用方式，共计6 种情形。也就是说，对于占用同一股道的2 列待检动车组，假如都将进行同一类型的2项作业p和q，无论是p在前还是q在前，2 列动车组作业无冲突下的股道实际占用情形必然在这6种情形之中且必然唯一，即

然后，针对图3中的3 种情形，进一步分析时间先后对列位占用的约束。

当实际占用情形为情形1时有

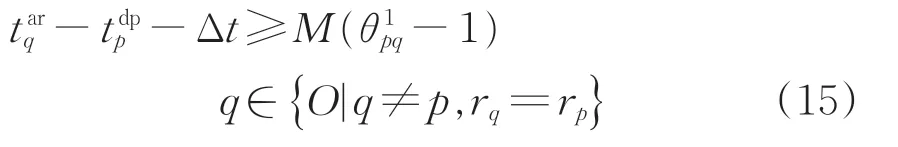
当实际占用情形为情形2时有

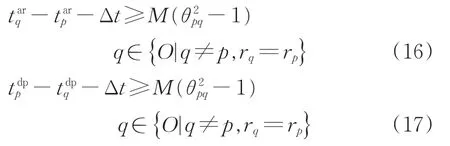
当实际占用情形为情形3时有

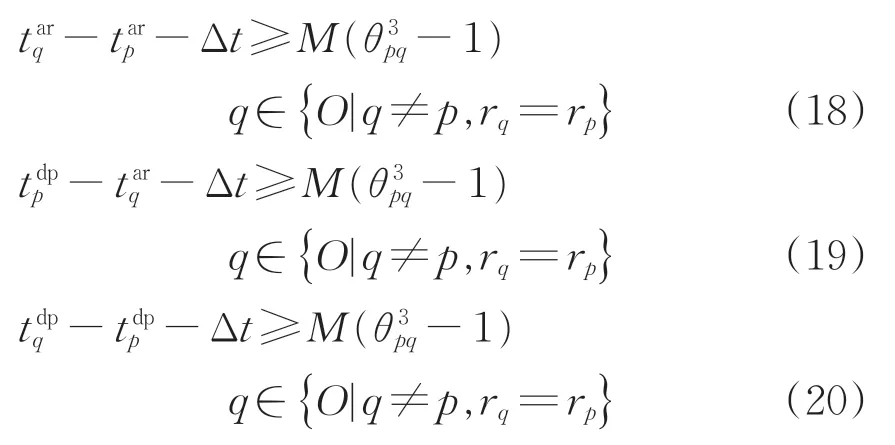
最后，结合动车所的具体布置形式，还有可能出现以下4种例外情况。

假如作业p和作业q的作业线区为通过式时（φrp=1），则不可能出现情形2，即

假如作业p和作业q的作业线区为尽端式时（φrp=0），则不可能出现情形3，即

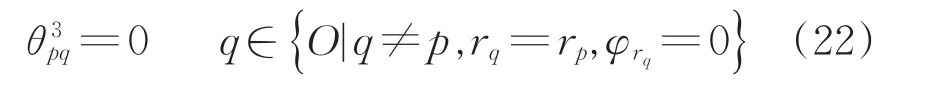
假如作业p和作业q归属的动车组中存在长编动车组，则不可能出现情形2和情形3，即

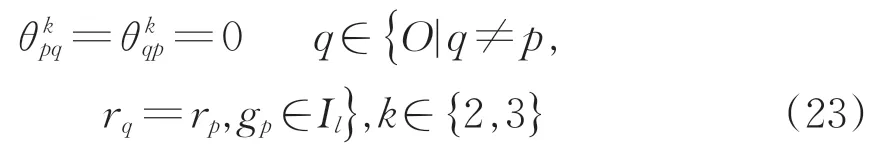
假如作业p和作业q不属于同一作业类或p=q时，则前述3种情形均不可能出现，即

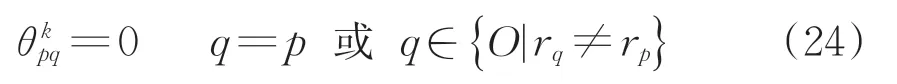
需要注意的是，本模型只求解了短编动车组共同占用通过式车场股道的起讫时刻。通过式车场的股道2 端各连接有1 处咽喉，且这2 处咽喉都可用于转线作业，因此，实践中具体占用哪个列位可视咽喉的忙碌情况和现场的作业条件来决定，给动车所调度员提供一定的灵活选择空间。

3.2.2 第二优先级模型

设Z*1为第一优先级模型的最优值，为确保第二优先级模型的求解不会导致更多的关键线区总占用时间，需将式（1）作为约束条件加入到第二优先级模型中。在同样需满足约束式（2） —式（24）的前提下，第二优先级模型的目标是最小化总存车次数，即目标函数Z2为最小化总存车次数正偏差量。

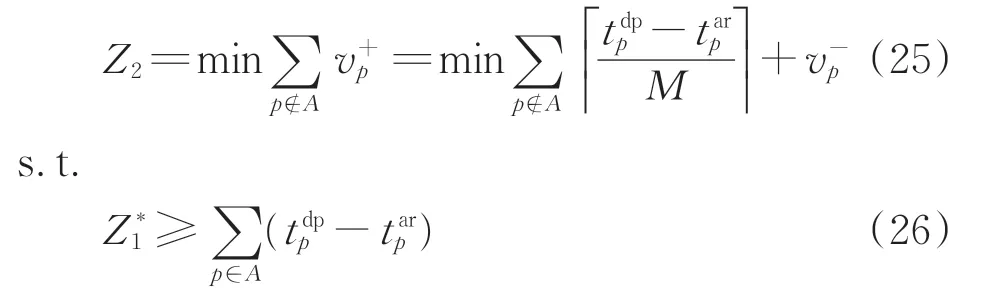
4 算例分析

参考文献［2］中的算例，依托图1（a）纵列式二级二场布置的某动车所，设计算例并运用CPLEX 进行求解。该动车所的配置有尽端式检修线4 条，尽端式轮对镟修线1 条，通过式清洗线2条，通过式吸污线1条，通过式存车线10条。检修作业内容规范见表1。在检修当日17：00—第3日7：00 的某计划期期间，在动车所内进行检修维护的动车组共有14列，检修计划见表2。表中股道占用和执行进路的安全间隔时间Δt按照平均时间计算，设为5 min。

为减少调车次数，参考文献［2］，将在相同线区开展的若干作业合并进行，例如将编号为2 的动车组的“一级修”与“18 万km 检修包”这2 项同在检修线区进行的作业合并进行，作业总时长为6 h。这样处理之后，必要作业共有34 项，最大可能总存车次数为48次。

在配置i7-8 550U CPU 和16 GB RAM 的计算机上，运用Visual Studio 2019 平台编程，调用数学求解工具CPLEX 实现对目标规划二级模型的求解［21］，并通过CPLEX内置的最大求解时间参数和优化间隙（Optimality Gap）参数设定求解程序的效率和质量。

将动车所设备数据以及表1和表2数据代入程序中，计算动车组各项作业所占用的股道以及占用起讫时刻，第一优先级模型求解耗时104 s，此时生成的作业计划关键线区占用总时长为5 880 min，各动车组总存车次数为40 次。分析可知，动车组对关键线区占用总时长已达到理论最小值，但是总存车次数接近理论最大值，调车成本较高，仍有较大的优化空间。

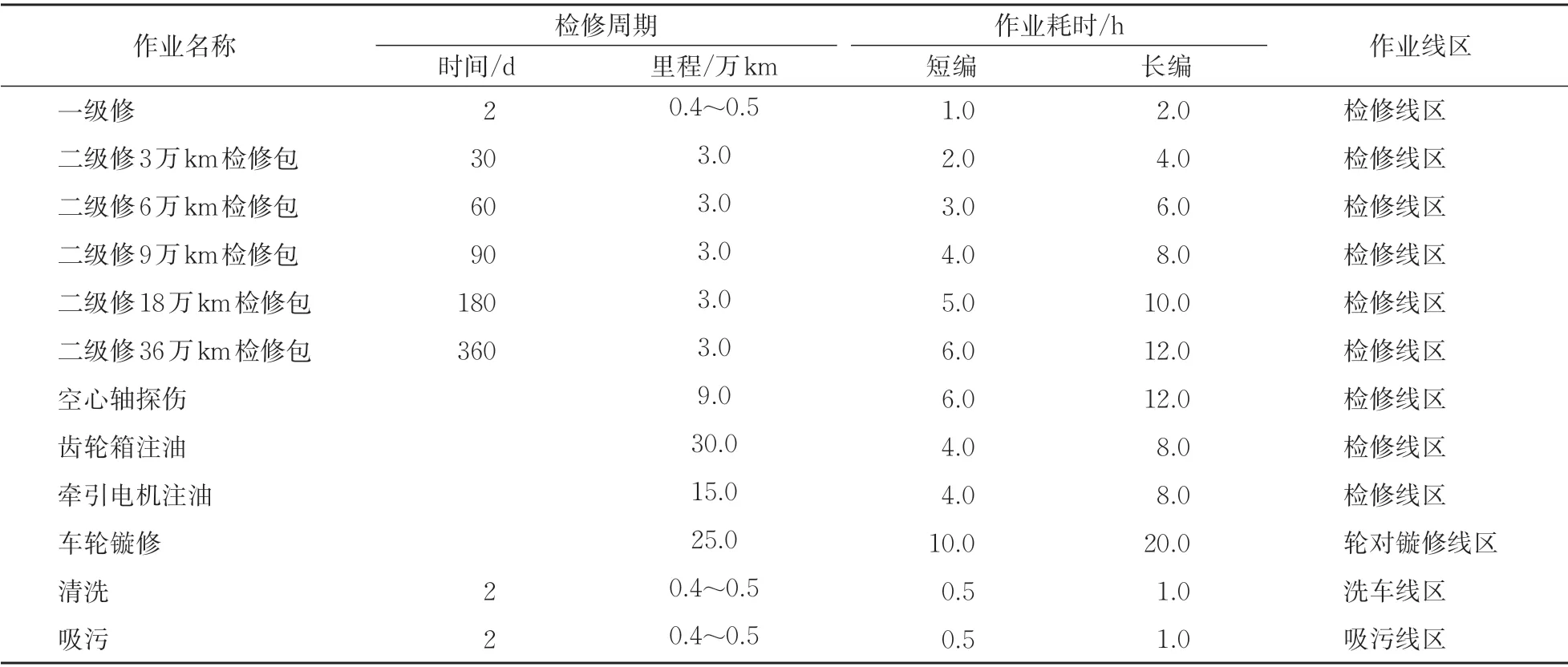
表1 某动车所检修作业内容规范

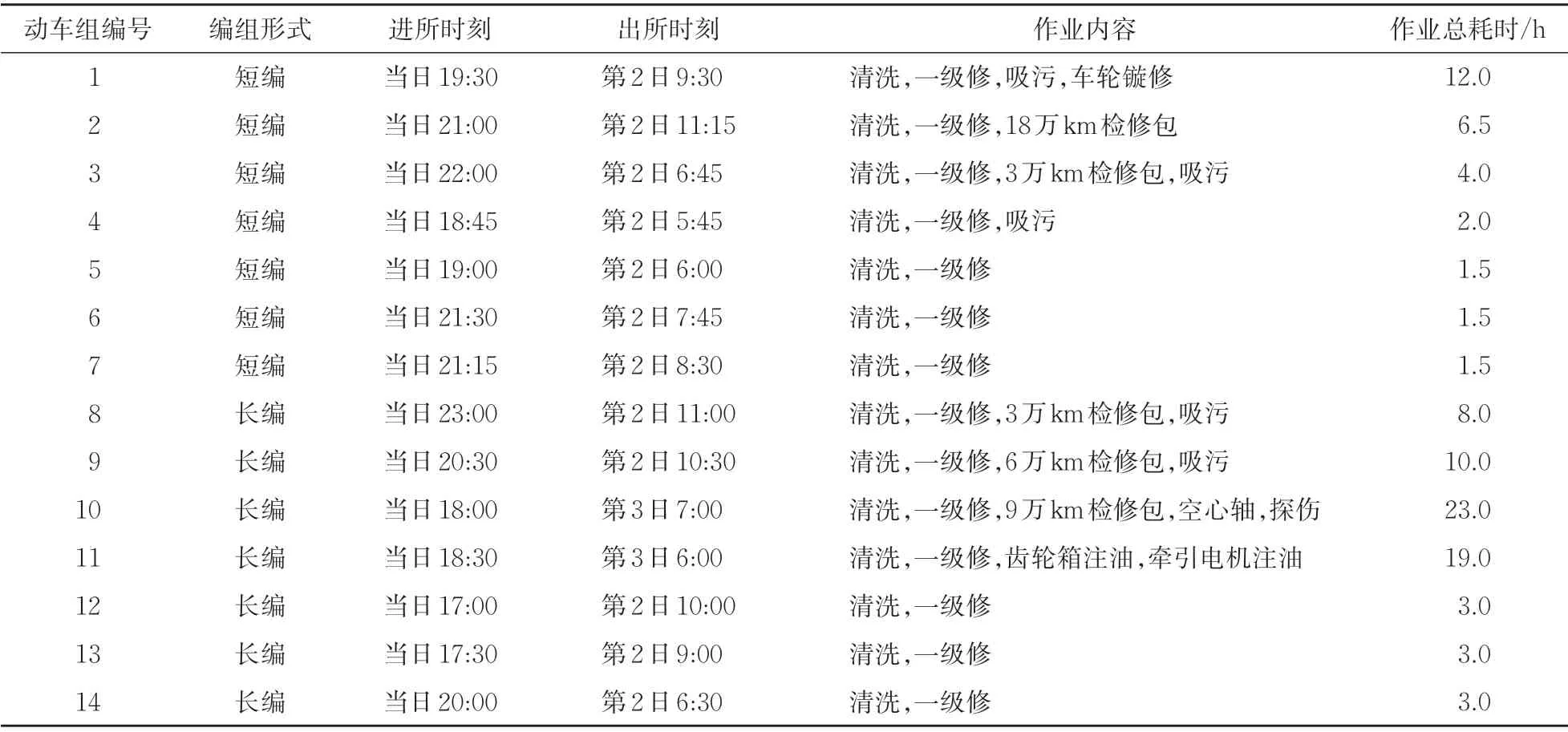
表2 某动车所检修计划

将第二优先级模型的最大求解时间设置为150 s，在不降低第一优先级模型关键线区总占用时间的前提下，计算生成的较优解即作业计划总存车次数为25 次，相比第一优先级模型的求解结果减少存车次数15 次，减少总存车次数达37.5%，此时的完整股道占用情况见表3。为便于计算，以计划期当日17：00 为时刻0，将时间转化为整数形式，例如计划期当日17：00—第3日7：00 可转化为0—2 280 min。表3中：小括号内数字为动车组编号；方括号内为该动车组对股道占用的开始时刻至占用结束时刻。

从表3中可以看出：股道利用方面，大部分股道的占用情形为图3中情形1，2 列短编动车组同时占用同一股道的情况共出现5次（尽端式车场检修线M2 出现图3中情形2，通过式车场吸污线P1和存车线S2，S3，S6 分别出现情形3 共4 次），表明本文模型有效利用了股道的双列位条件，提高了股道利用率；灵活存车方面，大部分动车组完成检修作业仅需存车1～2次，仅有2列动车组（动车组1和动车组6）需要存车3次，表明本文模型能够有效地降低动车组总存车次数以及相应的调车作业，使检修完毕的动车组尽快腾出当前作业股道，在检修资源日益紧张局面下，这有利于提高检修资源利用率，降低计划编制难度。

表3 优化后的动车所股道占用情况

在实际工作中，决策者往往要求在短时间内得到可行且较优的计划，因此需要谋求求解时间与求解质量之间的平衡。例如，将第二优先级模型的求解时长增加到600 s 后，求得的总存车次数为24次，仅较之前减少1 次，优化效果不够明显。因此，求解时间的设定需要结合实际情况来设定，也可以同时设置求解时长参数和优化间隙值参数来约束求解效率与求解质量。

5 结 语

以适用于带有不同车场布置类型的动车所为前提，重点考虑灵活存车、列位占用问题，在统筹各项检修作业先后顺序安排、进路冲突、车场布置类型等现实情况的基础上，建立了可用于动车所调车作业计划优化的字典排序目标规划二级模型，第一优先级模型以最小化关键线区总占用时间为目标，第二优先级模型以最小化总存车次数为目标。二级模型中，以动车所内的所有待开展作业为模型主要索引，通过决策所有作业的股道占用情况，得出所有待检修动车组的调车作业计划。

依托采用纵列式二级二场布置的某动车所设计算例，运用数学求解工具CPLEX 完成算例求解，证明第一优先级模型生成的动车所调车作业计划虽然实现了关键线区总占用时间最优，但存在总存车次数过多的问题；第二优先级模型在不降低关键线区总占用时间的前提下，减少存车次数达37.5%，降低了调车成本。通过目标规划二级模型，能够统筹调度动车所内的所有作业任务，有效压缩关键线区总占用时间和不必要的存车作业次数，为动车所调车计划的自动化编制提供理论参考。

需要注意的是，本文只考虑了咽喉同时单进路的情况，后续将会针对平行作业的同时多进路情况进行下一步研究，将调车进路细化到对道岔、列位等设备的占用。此外，如何将动车所内部调车计划与动车组运用计划、车站计划联合编制也是下一阶段的研究方向。

本文提出的模型索引方式不仅可用于运输调度，还可用于工业界加工处理一批带有不同作业内容的工件的场景，从而更为高效地处理柔性作业车间调度或柔性流水车间调度问题。