基于自适应联邦滤波的列控车载设备测速测距算法
2022-02-16杨志杰程剑锋李一楠
张 淼,杨志杰,程剑锋,李一楠
(1.中国铁道科学研究院 研究生部,北京 100081;2.中国铁道科学研究院集团有限公司 通信信号研究所,北京 100081)
测速测距是列控车载设备的关键技术之一。列控系统行车许可的生成必须依赖列车的速度和位置,因此列控车载设备实时、准确地采集和计算列车运行速度和走行距离尤为重要[1]。考虑到转速传感器实现较简单、受环境与地形限制小、测量精度与可靠性高等优点,传统的测速测距系统普遍采用转速传感器技术。为了保证测距测速系统的互补和冗余关系,一般将2 个转速传感器分别安装在不同轮轴处,车轮旋转1 周转速传感器会产生固定的脉冲个数,结合单位时间内的脉冲计数和车轮直径,即可得到列车运行速度;再对速度积分,即可得到列车走行距离。
测速测距系统的主要功能需求为计算当前列车的加速度、运行速度和走行距离,利用列车运动模型来描述列车的加速度和运行速度随时间变化的规律,但其建模过程中会不可避免地产生系统状态噪声,转速传感器也会受外界环境影响而产生测量噪声。这2 种噪声带来的偏差常被近似为零均值高斯白噪声,故采用对白噪声有很好抑制效果的卡尔曼滤波,能提供统计意义上的最优估计。
已有文献对测速测距系统核心算法进行研究,但多存在不足。文献[2]基于卡尔曼滤波,针对高速列车测速测距系统建立了恒速和恒加速的列车运动模型,并进行仿真验证,但其提出的恒速模型对加速度变化不敏感,对列车速度变化的感知存在延时效应,且恒加速模型在处理加速度变化大的临界点时会出现“超调现象”。文献[3]在建立列车运动模型时综合考虑了牵引力、制动力、运行阻力、坡度和弯道阻力等因素,但实践中测速测距系统无法直接获得上述变量的取值,而是通过加速度计或模型方法直接获取列车运行加速度进而得到列车运行速度。文献[4]介绍了当轮对受轨面条件、环境气候和列车运行状况等影响时,列车会发生空转/滑行,影响计算结果准确度,随着空转/滑行时间的增加,仅依靠单一的加速度计会发生漂移,导致累计误差增大。文献[5]基于滑模控制的卡尔曼滤波融合转速传感器和加速度计信息,虽然实现了空转/滑行误差降低、定位精度提升,但仅对仿真数据进行分析说明。文献[6]利用转速传感器和雷达,建立了空转/滑行检测及误差校正计算模型,然而雷达的使用条件苛刻,既要保证安装精度,又会受到天气、轨面状况等因素影响,故障率偏高。
本文在仅采用转速传感器技术的基础上,提出1 种基于自适应联邦滤波的列控车载设备测速测距算法,先建立自适应参数列车运动模型,对每个转速传感器的采集数据进行卡尔曼滤波处理;再利用检测方法判定列车空转/滑行情况,通过空转/滑行速度校正模型得到虚拟传感器的输出,即空转/滑行校正速度;然后根据实际情况动态调整信息分配系数,利用联邦滤波算法将自适应参数列车运动模型和空转/滑行时速度校正模型的计算结果进行数据融合,得到列车运行速度和走行距离。通过列车正常运行场景和制动时轮对滑行场景下的仿真分析,验证算法应用于列控车载设备测速测距系统的准确性和安全性。
1 自适应参数列车运动模型
在列车运行过程中,司机会施加牵引或制动,列车也会因为弯道和坡度变化而改变加速度,故列车在实际运行中很难保持恒加速状态。为能更好地跟踪列车运动趋势,在速度及加速度变化较大时仍能实时追踪列车运行速度,故选取自适应参数机动目标模型估计方法[7],建立自适应列车运动模型,由状态方程和测量方程组成。
考虑到测速测距系统需要在线处理大量数据,此处选用二阶矩阵自适应参数列车运动模型,以列车运行速度v和加速度a为状态变量,以便在较短的处理时间内得到较优的滤波结果。计算时,以机动频率α和加速度方差δ2作为模型的自适应参数,先利用状态方程预测列车运行状态和协方差,在获得预测结果的基础上,结合实际测量值更新列车运行状态,估计当前状态下的列车运行速度v和加速度a;再根据列车加速度估计值,实时修正自适应参数α和δ2,并不断更新列车运动模型和系统状态噪声,最终实现模型计算结果与列车实际运动状态趋于一致。
1.1 状态方程
由于转速传感器无法直接观测量到列车运行加速度,故采用列车运行过程中前2 个周期估计加速度的均值作为状态方程的加速度,取列车运行时的速度v和加速度a作为状态变量,则状态向量x=(v,a)T,构造状态方程可表示为

式中:k为当前时刻;T为k−1 至k时刻的测速测距采样周期;xk−1和xk分别为k−1 时刻和k时刻下的状态向量;A为状态转移矩阵,Ak,k−1描述了系统状态从k−1 至k时刻的变化规律;U为输入控制矩阵,Uk,k−1引入加速度参量来描述k−1 至k时刻外力的作用;为k−2时刻至k−1时刻的列车估计加速度均值;Wk−1为k−1时刻下的系统状态噪声,假设其是均值为零、方差为Qk−1的白噪声矢量。
利用系统的自适应参数可对对称矩阵Qk−1实现实时调整,矩阵元素分别用q11,q12,q21和q22表示,即

其中,

式中:E为期望;rk−1(0)为k−1 时刻列车加速度估计值的自相关系数;rk−1(1)为k−1时刻与k−2时刻列车加速度估计值的相关系数。
1.2 测量方程
测速测距系统中,利用已知的转速传感器齿数M和车轮直径D,可得到转速传感器每转过1 个齿对应的列车走行距离为若1 个测速测距采样周期T内采集到的脉冲为n个,那么转速传感器的采样频率f=测量速度v=则列控车载设备测速测距系统的测量方程可表示为

式中:Zk为k时刻下的测量值,在取值上与fk相等;fk为转速传感器在k时刻的脉冲频率;Hk为测量矩阵;Vk为k时刻下的转速传感器测量噪声,假设其是均值为零、方差为Rk的白噪声矢量,且与系统状态噪声Wk相互独立。
2 空转/滑行时列车速度校正模型
受列车运行状况、轨面条件和环境气候等因素影响,列车运行过程中轮对容易发生空转/滑行,此时转速传感器测得的列车运行速度与实际情况间会出现较大偏差,并且这一偏差无法仅凭转速传感器自身进行有效修正[8]。
为解决该问题,设计列车速度校正模型,并将其视为1 个虚拟传感器,与安装在不同轮轴上的2个转速传感器共同构成列控车载设备测速测距系统。列车速度校正模型可快速检测出转速传感器所在轮对的运行状态,当2 个轮对均出现空转/滑行动作时,便由速度校正模型获取并计算空转/滑行状态下的列车运行速度和走行距离,以便获取的结果更为准确。
2.1 空转/滑行检测方法
按照列车轮轴的动力形式(是否带有牵引力或制动力),车轮可划分为带制动的动力轮、带制动的从动轮和不带制动的从动轮这3类,其中带制动的动力轮较易发生空转和滑行,带制动的从动轮较易发生滑行,不带制动的从动轮不易发生空转和滑行[9],因此空转和滑行检测需要分车轮情况具体讨论。
常规的检测空转/滑行的方法主要有滑移率法、速度差法和加/减速度检测法[10],这3 种方法既可单独使用也可组合使用,使用时根据不同车型的牵引和制动性能选取相应判据参数。为能检测到较微弱的列车空转/滑行情况,在这3 种方法的基础上,本文再引入加/减速度变化率的检测方法[11],结合列车轮轴类型检测轮对是否处于空转/滑行状态。
1)变量定义
当列车以速度v、加速度a运行时,第i个转速传感器所在轮对的运行速度为vi(i=1,2),加速度为ai,相应的加速度变化率(加加速度)为ji=则当前测速测距采样周期下2 个轮对的速度差为Δv=|v1−v2|。
为描述车轮的滑行程度,定义车轴对应车轮的滑移率λi为列车在制动时车轮的抱死程度,则λi=当车轮完全抱死纯滑动时取λi=1。同理,为描述车轮的空转程度,定义车轴对应车轮的滑转率λri为列车加速起步时车轮的滑转程度,即λri=×100% ,当车轮滑转完全不前进时取λri=1。
由于不同车型的牵引和制动性能并不相同,考虑通过调整门限值的形式来适应不同车型的空转/滑行情况,设速度差门限为Δvlim,最大加速度门限为amax,最大减速度门限为amin,滑移率门限为λlim,滑转率门限为λrlim。
2)空转检测
对于较易发生空转的带制动动力轮,当a>0时首先对每个转速传感器所在轮对分别进行检测;经过测速测距采样周期T后,若ai+jiT>amax或λi>λlim这2 个条件任一成立,则检测到此转速传感器所在轮对发生空转;若此时还满足Δv>vlim的条件,由于2 个转速传感器所在轮对互为参考,无法判定到底哪个轮对发生空转,考虑安全性,检测结果为这2个转速传感器所在轮对同时发生空转。
3)滑行检测
对于较易发生滑行的带制动动力轮和带制动从动轮,当a<0 时首先对每个转速传感器所在轮对分别进行检测;经过测速测距采样周期T后,若ai+jiT
2.2 列车速度校正模型
检测到空转/滑行后,需要通过列车运行速度校正模型获得准确且安全的列车运行速度和走行距离。校正时,根据不同车型车辆的空转/滑行程度和黏着恢复情况,设定相应的空转/滑行持续校正时间。为简单起见,以amax和amin分别作为速度校正模型的加速度和减速度。
当检测到2 个转速传感器所在轮对同时发生滑行时,记其在上个测速测距采样周期的速度为vbefore,加速度为abefore。在vbefore的基础上,需计算k时刻下的列车校正速度vcorrect(k),即
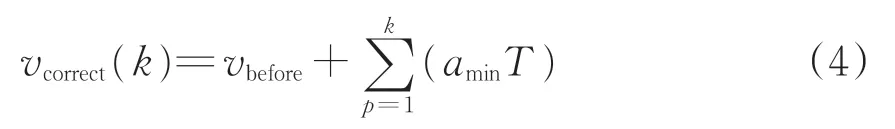
在滑行持续校正时间内,实时监测车轮轮轨黏着恢复情况,将2 个转速传感器所在轮对的测量值与校正后的速度进行比较,以vi>vcorrect时记作时刻n,此时车轮轮轨黏着已经恢复,
校正速度不应小于车轮轮轨黏着恢复后的速度,故增大列车校正速度,即
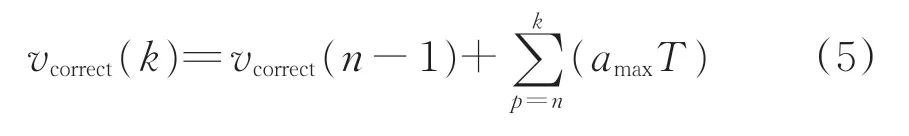
待校正速度大于2 个转速传感器的测量速度,即vcorrect>vi后继续以式(4)推算列车运行速度,校正距离即为校正速度的积分。
列车减速滑行运行过程中,当车轮抱死时测量速度v1和v2同时为零,此时测速测距系统缺乏有效的测量值,因列车运行速度不可能突变,综合考虑可用性和安全性,取较小的默认减速度作为校正减速度并继续推算列车运行速度,使列车运行速度平稳下降直至列车完全停止(即校正速度为零)。
空转时情况与滑行时相反,先以速度校正模型的加速度求解速度,当车轮轮轨黏着恢复后,校正速度不应大于车轮轮轨黏着恢复后的速度,故减小列车校正速度。校正结果同样成立,不再展开。
列车速度校正模型基于加速度二重积分法[12−13]获得计算速度和距离,同时考虑了转速传感器实时的测量值,这样通过计算速度与测量速度的不断比较,能够不断修正校正速度和校正距离,使获得的列车运行速度和走行距离符合车轮轮轨实际黏着情况。
3 基于联邦滤波的数据融合算法
3.1 测速测距数据融合结构
基于联邦滤波的融合算法具有容错性能好、融合结果精确、计算量小等优点[14],且联邦滤波结构能够保证数据先分散处理、再全局融合,通过时间更新和测量更新进行算法递推,以融合后的全局最优估计值作为系统的最终输出结果,因此在列控车载设备测速测距系统中采用基于联邦滤波的融合算法。
设计列控车载设备测速测距系统由2 个转速传感器和1 个虚拟传感器(空转/滑行速度校正模型)共3 个部分组成,其算法框图如图1所示。图中:箭头表示数据流的走向;为全局状态估计;Pf为协方差矩阵;(i′=1,2,3,i′=3 时代表虚拟传感器)为转速传感器对应子滤波器的状态估计,由速度和加速度估计值构成;Pi′为子滤波器状态估计的误差协方差矩阵;βi′为3 个子滤波器的信息分配系数,

图1 基于联邦滤波的测速测距数据融合结构
列车实际运行过程中,测距测速系统难免会受到外界的电磁干扰,测速齿轮箱体和转速传感器也有可能在钢轨衔接处受到振动的影响,这些情况都将导致转速干扰信号的产生。为避免轮速发生突变造成空转/滑行的误判,在数据融合处理前,先要对测量结果进行数据预处理[15]。
由图1可知:2 个转速传感器输出的数据分别经过数据预处理去除干扰信号,输出转速传感器有效测量值;校正模型作为虚拟传感器,输出转速传感器所在轮对发生空转/滑行时的列车校正速度;将测量值和校正值分别输入3 个相互独立、并行运行的子滤波器,其中2 个转速传感器对应的子滤波器1 和子滤波器2 均采用自适应参数列车运动模型,得到转速传感器所在轮对速度和加速度的估计值,与子滤波器3 得到的校正速度估计值共同描述列车运行的动态过程;最终由主滤波器根据列车空转/滑行情况和转速传感器的滤波估计值动态调整信息分配系数,主滤波器数据融合得到的状态估计值即为列车运行速度和加速度。
在联邦滤波算法中,将系统噪声Qf和状态协方差Pf通过信息分配系数βi′分配到各子滤波器,信息分配系数βi′满足信息守恒原理并能随着系统状态的动态变化进行相应调整,以增加系统的安全性和鲁棒性,即

主滤波器和各子滤波得到的状态估计(k)与协方差矩阵Pi′(k)对应融合,得到全局状态估计及协方差矩阵,即

其中,

3.2 动态调整信息分配系数方案
确立信息分配系数方案是建立基于联邦滤波的列车测速测距系统的关键[16]。对信息分配系数β值的动态调整方案需要满足以下速度处理安全原则。
(1)当检测到某1 个转速传感器所在轮对发生空转/滑行时,为减少空转/滑行轮对的采集数据影响,将此轮对的信息分配系数取值调小,另1个轮对的则相应调大。
(2)当检测到2 个转速传感器所在轮对同时发生空转/滑行时,采用空转/滑行校正策略得到列车运行速度,2 个轮对的信息分配系数取值均调小,列车校正速度的信息分配系数相应调大。
(3)当检测到2 个转速传感器所在轮对均正常但存在速度差时,从控车安全性角度出发,速度值较大轮对的车轴信息分配系数取值较大,速度值较小的信息分配系数取值也相应较小。
在满足上述安全原则的基础上,设进入子滤波器的数据为1个包含速度和状态信息的向量,对于2个转速传感器,若检测到传感器所在轮对发生空转/滑行则状态值Si取0,否则Si取1;对于虚拟传感器,状态值此时信息分配系数βi′(k)的动态表达式为

由于存在分配系数的倒数运算,βi′(k)不能取0,故计算时取极小值。
根据不同的运行情况动态,利用式(8)调整得到相应的信息分配系数后,通过基于联邦滤波的数据融合算法,可将自适应参数列车运动模型和列车速度校正模型的计算结果进行滤波融合,输出列车运行速度;再对速度积分,即得到列车走行距离。
4 测速测距算法的仿真及结果分析
为验证基于自适应联邦滤波的列控车载设备测速测距算法的应用性能,利用接口型式实验采集转速传感器测量数据和MATLAB 仿真软件进行仿真分析。分别取型式实验中列车正常运行场景和制动时轮对滑行场景下的测速测距系统监测数据,分析列控车载设备测速测距算法是否满足准确性和安全性要求。
4.1 列车正常运行场景
选取列车进、出站及在区间中正常运行的场景,将每个轮对现场采集速度叠加噪声后作为测量值、参考值(即真实值)分别与采用自适应参数列车运动模型得到的滤波结果进行对比,如图2所示。图中:速度的采样周期取0.05 s;采样点个数为0 时表示采样开始时刻,采样点个数与采样周期的乘积表示当前采样时刻。由图2可知:采样点4 000个左右,即采样开始200 s时(4 000×0.05 s=200 s),列车加速度开始发生较大变化,从加速度为零变为加速度为正;采样点11 500个左右,即采样开始575 s 时(11 500×0.05 s=575 s),列车加速度开始从零变负;滤波结果和速度参考值变化趋势一致,这表示自适应参数列车运动模型能有效滤除噪声;滤波结果对加速度变化敏感,在速度变化的过程中也不存在滞后现象,满足测速测距对准确性的要求。

图2 列车正常运行仿真结果
4.2 列车制动时轮对滑行场景
以涂洒减磨液的形式制造滑行场景。考虑列车制动过程中可能发生的2 种情况:一是单个转速传感器所在轮对发生滑行;二是2 副轮对同时发生滑行。分情况测量2 个转速传感器所在轮对的运行速度数据,采用基于自适应联邦滤波的测速测距算法模型进行仿真。单个转速传感器所在轮对发生滑行时的算法仿真结果如图3所示。图中:传感器1 和传感器2 分别为2 个安装在不同轮轴上的转速传感器;红线和绿线分别表示不同转速传感器所在轮对的测量值通过列车运动模型得到的估计速度;黑线表示列车运行速度。由图3可知:采样点750 个左右,即采样开始37.5 s 时(750×0.05 s=37.5 s)可视之为分界点;37.5 s之前列车正常运行,信息分配系数权重相当,这表明联邦滤波融合结果同时考虑了2个转速传感器所在轮对的测量速度;37.5 s之后,利用空转/滑行检测方法检测出传感器2 所在轮对发生滑行,于是减少对其信息分配系数的权重,联邦滤波融合结果主要基于传感器1所在轮对的速度,因此列车运行速度基本没有受到滑行的影响,满足列控车载设备测速测距对准确性和安全性的要求。

图3 单个转速传感器所在轮对滑行场景下的仿真效果
2 个转速传感器所在轮对同时发生滑行时的算法仿真结果如图4所示。由图4可知:采样点12 个左右,即采样开始1.6 s 时(12×0.05 s=1.6 s),利用滑行检测方法检测出2 个转速传感器所在轮对同时发生滑行,此时主要由列车速度校正模型计算列车运行速度;采样点40个左右,即采样开始2.0 s时(40×0.05 s=2.0 s),传感器1 所在轮对的速度超过了校正后的列车运行速度,此时转速传感器所在轮对黏着恢复,校正速度由4.2 m·s−1调整为4.7 m·s−1,在滑行持续校正时间内继续利用滑行速度校正模型计算校正速度;采样点150 个左右,即采样开始7.5 s时(150×0.05 s=7.5 s),2 个转速传感器所在轮对的速度均为零(滑行期内若2 个转速传感器的测量速度为零,则视之为车轮抱死),此时列车还在减速运行,为保证测速测距的安全,在原有校正速度的基础上,取较小的减速度计算列车运行速度直至列车完全停止,整个速度计算过程满足列控测速测距对准确性和安全性的要求。

图4 2个转速传感器所在轮对滑行场景下仿真效果
可见,无论是列车正常运行场景还是制动时轮对滑行场景,无论滑行的是单个转速传感器所在轴的轮对还是2 副轮对,本文算法均能够自适应地跟踪列车运行速度,通过实时检测转速传感器所在轴的空转/滑行情况,在安全导向的前提下得到符合车辆运行实际情况的列车运行速度,兼顾了列控车载测速测距系统对准确性和安全性的要求。
5 结 论
(1)提出1 种由自适应参数列车运动模型、空转/滑行时列车速度校正模型和基于联邦滤波的融合算法3 部分组成的列控车载设备测速测距算法,仅使用2 个转速传感器,即可实现对转速传感器所在轮对当前测量速度的实时、有效修正,克服了以往测速测距系统中转速传感器因所在轮对空转/滑行引起的速度测量精度下降问题,更符合列车实际运行情况。
(2)建立自适应参数列车运动模型,2 个转速传感器采集得到的速度脉冲信号经过预处理后,可分别得到其所在轮对的估计速度和加速度,在列车运行加速度变化较大时,仍能够实现对转速传感器所在轮对速度的实时追踪。
(3)设计速度校正模型并将其视为1 个虚拟传感器,能够在检测确定2 个转速传感器所在轮对空转/滑行情况的基础上,通过校正速度与测量速度的不断比对与修正,与自适应参数列车运动模型共同描述列车运行的动态过程。
(4)利用基于联邦滤波的融合算法,设计动态调整信息分配系数方案,实现自适应参数列车运动模型和列车速度校正模型的计算结果的有效融合,使得到的运行速度和走行距离能够反映出列车实际运行状态。
