基于Q学习算法的摘挂列车调车作业计划优化
2022-02-16施俊庆陈林武林柏梁孟国连夏顺娅
施俊庆,陈林武,林柏梁,孟国连,夏顺娅
(1.浙江师范大学 工学院,浙江 金华 321004;2.浙江师范大学 浙江省城市轨道交通智能运维技术与装备重点实验室,浙江 金华 321004;3.北京交通大学 交通运输学院,北京 100044)
调车作业计划是规定车辆如何调移及其作业程序的具体行动计划。按站顺编组摘挂列车是指将调车场某调车线上集结的去往前方中间站的车辆,从杂乱无章到按到达中间站的顺序进行编组的过程,是一项十分复杂而重要的工作。
调车作业计划的质量决定了车站调车工作的效率[1],许多学者对此展开深入研究,力求不断提高编制质量。文献[2]提出了“表格调车法”,将摘挂列车车辆编组顺序问题转变为1 种编号问题,减少了调车钩数和占用的调车线数。文献[3]提出了“统筹对口调车法”,将编组调车过程描述为一系列连续的对口过程,优化了选编调车的连挂钩数。文献[4—5]根据编制钩计划条件下的调车方案及摘挂列车下落等特点,提出变异方案的概念和“消逆法”调车作业理论,改进了调车作业编制方法。文献[6]分析了车组隔离、股道数量限制等情况下的编组摘挂列车钩计划优化问题。文献[7]将摘挂列车下落问题抽象为排序问题,提出了1种基于排序二叉树的编组钩计划自动编制方法。文献[8]在改进“分析计算法”的基础上,提出溜放钩数计算式,优化了调车方案的选择。文献[9]提出了基于分支定界法的摘挂列车编组优化算法。
随着信息技术的进步,传统的优化算法已无法满足铁路调车工作决策智能化发展的需求,强化学习的出现为此提供了新思路。强化学习技术是机器学习的1 个分支,从算法上看主要包括基于值的算法和基于策略的算法,可以作为支持调车工作智能化决策的有效工具。Watkins 于1989年首次提出的Q学习算法是1 种典型的基于值的算法,也是目前强化学习算法中应用最广泛且最有效的1 种算法[10—11]。在铁路智能调度方面,文献[12]根据车辆的位置、到达时间、停留时间等运行状况,基于强化学习方法对列车调度算法进行了改进;文献[13]以减少调车机车移动为目的,研究了基于Q学习算法的货车调度优化问题。在列车运行控制方面,文献[14—15]通过预测列车的运行状态和调车计划等,运用强化学习技术和深度Q学习算法研究了列车的控制方法;文献[16]引入带轨迹的延迟奖励,结合Q学习算法研究了列车运行调整问题,减少了相应的计算时间。
本文将强化学习技术和Q学习算法应用于摘挂列车编组调车作业计划优化问题。在表格调车法的基础上,通过动作、状态和奖励3 要素的设置构建强化学习模型,改进Q学习算法,以最小化调车程为目标建立待编车列和最佳调车作业方案之间的映射关系,智能体学习充分即累加Q值达到收敛状态时,计算得到优化后的调车表及调车作业计划。
1 问题描述
沿用文献[1]中的表述描述调车作业计划编制问题,用阿拉伯数字代替车组到站,并规定距离本站最远的车组到站为“1”,从远到近依次编为2,3,…,调车机车在调车场的右端作业,根据“按站顺编组”的要求,将待编车列中的车组连挂成列,并使列车编成后各车组的排列顺序为依次递增或相等。调车作业计划优化的本质是通过调车钩的安排,实现调车程的最小化。其中,调车钩指机车连挂或摘解1 组车辆的作业,分为“挂车钩”和“摘车钩”;调车程指机车或机车连挂车辆加减速1次的移动,通常情况1 个挂车钩对应于2 个调车程,1 个摘车钩对应于1 个调车程。调车作业计划的编制可用调车表来进行。调车表是调车场的示意图,横格为“列”,表示股道,竖格为“行”,表示车组在待编车列中的相互位置。假设:每个车组仅含1 辆车,牵出线及调车线的存车、调车机车的牵引能力等不受限制。
同时引入如下定义。
(1)接连:从左侧某车组起,相邻车组编号差值不大于1且为递增或相等的形式。
(2)非接连:与接连相对应,相邻车组不满足接连定义的其他所有形式。
(3)目标暂合列:调车表中非接连形式车组的所在列。
(4)非接连数:非接连形式的车组数量。相邻2 个车组组成非接连形式后,便会产生1 个非接连数。
例如,调车表中某列的车组编号依次为“1323456”。其中,相邻车组1 与3 之间的编号差值为2,该相邻车组构成非接连形式;相邻车组3与2 的编号为递减,该相邻车组也构成非接连形式;从第3个车组起,相邻车组2,3,4,5 与6 构成接连形式。该列为目标暂合列,非接连数为2。
2 调车作业问题的强化学习模型
在表格调车法的基础上,将调车作业计划分为下落和重组2 个部分,通过动作、状态和奖励3 要素的设置构建强化学习模型。
2.1 相关参数及定义
参数:K为某站实际可用的股道数量;L为待编车列中的车组数量;G为挂车钩数;D为摘车钩数;Z为调车机车最左端连挂的车组编号;Cij为调车表中第i列中第j辆车;Li为第i条股道上的车组数;Pi为第i条股道上的最右端车组编号,若第i条股道上没有车组,则不存在Pi。
编组列车时,为了调转待编车列中车组间的排序,需要将待编车列中的反顺序车组分解到不同的股道上,这种调车过程反映在调车表上,被称为下落[1]。任取待编车列“34172612537”的某一下落方案为例,所有车组下落后,各车组在调车场(调车表)中的位置见表1。表中:每1 格中的数字表示相应编号的车组下落到对应编号的股道上。由表1可知:此时K=5,L=11;对于第1 条股道,C11=3,C12=4,C13=5,L1=3,P1=5;存在唯一的目标暂合列,即i=4,此目标暂合列中仅车组7与6构成非接连形式,非接连数为1。

表1 初始下落方案调车表
将待编车列的最右端车组定义为端组。考虑到分解待编车列时,若端组为最大编号车组,对其进行下落操作可能会产生1 个多余的摘车钩。基于此,本文假设端组为最大编号车组时,根据下落方案所得的调车表,端组及其所在列左端直接相连的车组将连挂在调车机车上,不进行下落。例如在表1中,端组为最大编号车组(车组7),但调车表中其左端相邻位置并无车组,所以仅端组不下落。
2.2 强化学习的动作与状态
1)动作
以调车机车为智能体,将车组下落的股道编号定义为智能体的动作。用1个L维的行向量αn表示智能体对第n个车组的动作(1≤n≤L),αn中第n个分量记为an,表示智能体选择的股道编号,其余分量均为0。如果智能体可选择的动作有K种,则有动作集合A={1,2,…,K},但各车组可选择的动作均为K种时会存在大量重复解,为了减少重复性,规定第n个车组可选择的动作集合An(An⊆A)为
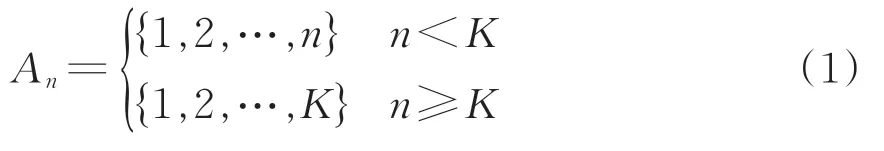
2)状态
为反映调车场对应的股道下落情况,以调车表为环境,将调车表简化为1 个L维的行向量Sn=(x1,x2,…,xL),用于表示第n个车组下落后的调车表状态,其中xn表示第n个车组下落后所处的股道编号。当第n个车组未下落时,xn=0;当第n个车组选择某1 条股道下落时,向量Sn中第n个分量变为所选股道编号an,并且状态发生1 次变化。设调车表的初始状态S0=(0,0,…,0),此时所有车组均未开始下落;调车表的目标状态SL=(a1,a2,…,aL),此时所有车组均完成下落。以表1为例,下落全部完成时该调车表对应的状态S11即为目标状态,S11=(1,1,2,4,3,4,2,2,1,3,4)。
3)状态更新规则
当调车表处于初始状态S0时,全部车组均未下落,此时,智能体对第1 个车组选择的动作为α1=(a1,0,0,…,0),据此更新的下1 个状态为S1。以此类推,在状态Sn−1下,智能体采取动作αn(αn∈An)后,下1个状态更新为Sn,即

式中:Sn为更新后的状态;αn为对第n个车组的动作。
以表1为例,当第4 个车组下落后,状态S4=(1,1,2,4,0,0,0,0,0,0,0),此时智能体对第5个车组的动作α5=(0,0,0,0,2,0,0,0,0,0,0),更新后的状态S5=(1,1,2,4,2,0,0,0,0,0,0)。
2.3 车组挂车、摘车条件和车辆重组流程
当所有车组均下落后,需要通过挂车和摘车对调车场上的车辆进行重组,以实现按站顺编组。挂车、摘车的具体条件及车辆重组流程如下。
1)挂车条件
条件1:存在Cij及其右端所有车组,都能与调车机车上连挂的车组构成接连形式,且股道中不存在比Cij大的车组。
条件2:按非接连数从大到小依次寻找目标暂合列,其中存在Cij=Pm或Cij=Pm+1,且i≠m。
条件3:全部由接连构成的列中存在Cij=Pm或Cij=Pm+1,且i≠m。
当满足以上任意1 条挂车条件时,将车组Cij及其右端的所有车组挂至调车机车上。
2)摘车条件
条件4:存在Pi,使Z=Pi。
条件5:存在Pi,使Z=Pi+1。
当满足以上任意1 条摘车条件时,将调车机车最左端的车组溜放至相应股道。
3)车辆重组流程
车辆重组的具体流程如图1所示。待编车列下落完毕后,其余车组需先根据调车表依次判断条件1—3,确定是否挂车;然后判断调车机车上所有车组是否构成接连且调车表中是否没有比Z大的车组,若成立,且调车表中存在剩余车组则继续判断挂车条件,直到不成立;再根据条件4—5 确定是否摘车,溜放车组直至调车机车上的所有车组构成接连形式,且股道中不存在比Z大的车组;此时,若本轮还未进行过挂车或摘车作业,需将Z车组随机溜放至任意股道,并再次判断摘挂条件;循环上述过程,直至调车表中无车组,最后获得调车作业计划表,并根据计划表得到挂车钩数G和摘车钩数D。
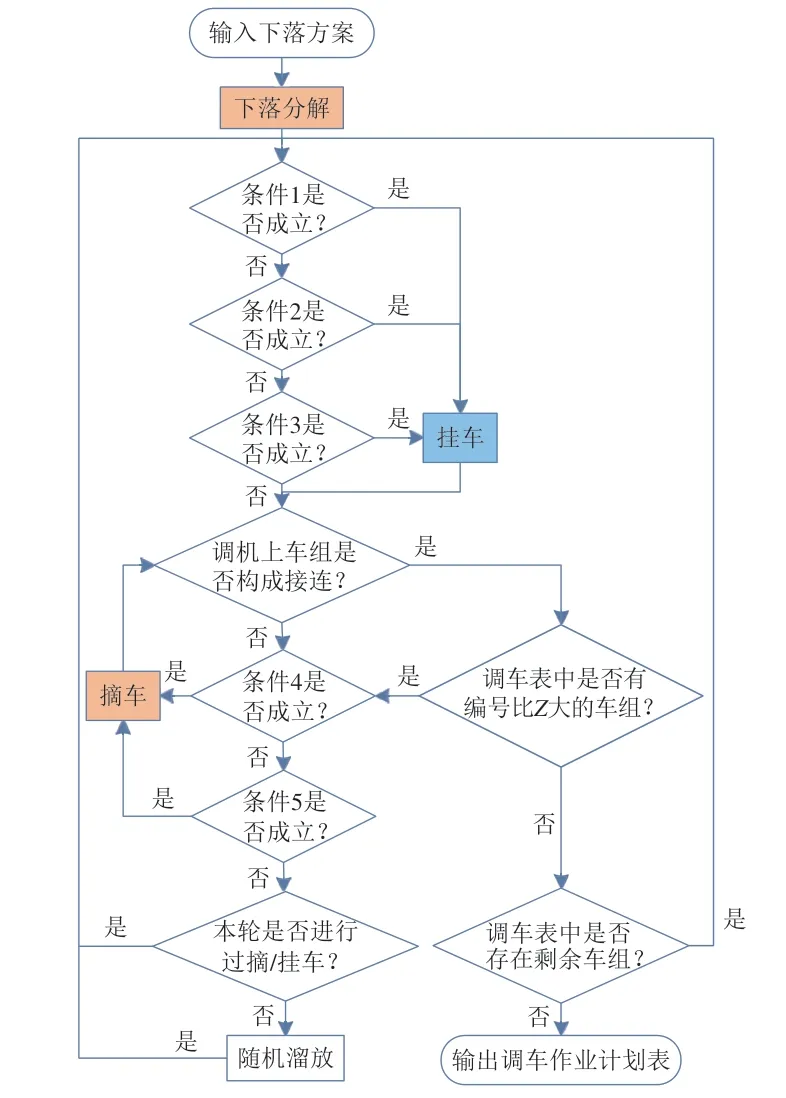
图1 下落后车组的重组流程
2.4 奖励函数设计
编组列车过程中,调车程的数量是评判下落方案优劣的主要依据。同时,下落后调车表中非接连数越多,需要的挂车钩就越多,调车程数量也会随之增加,因此根据车组下落后的接连状态及总调车程,分即时奖励和附加奖励2部分设计奖励函数。
根据车组下落后的接连状态确定即时奖励,规定下落过程中,对第n个车组执行动作αn后获得的即时奖励rSn−1,αn为

式中:λ为0-1 变量,当执行动作后能与所在股道上的相邻车组构成接连时取1;否则取0。
车辆重组后,根据调车程数量确定下落方案的附加奖励Rrestructure为

式中:φ为任意正数。
合并上述2 部分奖励,智能体每选择1 个动作后的累积奖励RSn−1,αn为

式中:RSn−1,αn为智能体在状态Sn−1时选择动作αn的累积奖励;m为1到n的自然数。
智能体依据环境状态选择动作,每次执行动作后,根据上述计算式确定累积奖励。当所有车组完成下落,即达到目标状态时,需根据车组下落和车辆重组过程得到调车作业计划表,并统计相应的挂车钩数和摘车钩数,计算附加奖励。调车作业计划表的优劣通过奖励函数体现,奖励函数计算得到的数值越大,意味着调车作业计划表越优。
3 Q学习算法改进
改进Q学习算法,对调车作业的强化学习模型进行求解。Q学习算法根据智能体执行每个动作后的累积奖励来决定状态与相应的动作之间的映射关系。映射关系通过Q值来表示,即智能体在状态Sn−1时选择动作αn能够获得奖励的期望。Q值越大,说明该状态下执行该动作越有利。求解前文模型时,在调车程最小化的目标下,构建待编车列与最优调车作业计划间的映射关系。以全部车组下落完毕为1 次迭代,每次迭代中,当第n个车组下落时,根据当前状态Sn−1,从动作集合An中选择可用的动作αn并执行,Q值根据迭代中的累积奖励进行更新。
使用动态的Q表来存储智能体学习所得到的经验知识,见表2。表中:每行数字中的第1 到L列构成状态,第L+1 列为该状态对应的Q值。在初始时刻,Q表仅记录了初始状态S0及其对应的Q值;每当状态发生变化时,Q表中该状态对应的Q值将被更新;若Q表中无该状态,则插入该状态及其Q值。智能体学习得到的最终Q表体现了待编车列和最优调车作业方案之间的映射关系。
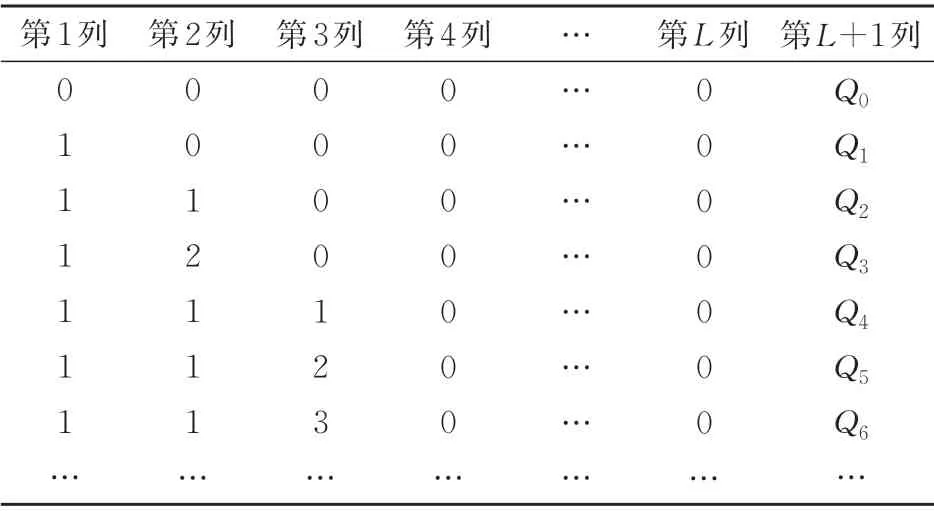
表2 智能体学习得到的动态Q表
第n个车组下落时,Q值的更新计算式为

式中:Q′n−1(Sn−1,αn)为状态Sn−1时智能体执行动作αn后更新的Q值,αn由策略π(α|S)决定,该策略表示状态S下选择动作α的概率;β为学习率,β∈(0,1],学习率越大,表示采用新的尝试得到的结果比例越大,保持旧的结果的比例越小;γ为折扣系数,γ∈(0,1],如果γ接近于0,则智能体会倾向于即时奖励,如果γ接近于1,则智能体会更多地考虑未来的奖励,愿意延迟奖励[11]。

其中,

式中:ε为智能体的探索率;y为迭代次数;argmaxQ(S,α)为状态S下使得Q值最大的动作。
将Q表中的Q值之和定义为累加Q值。设定连续1 000 步内累加Q值不发生变化即收敛。算法的具体过程如下。
步骤1:智能体开始学习,初始化Q表,确定待编车列,默认参数β=0.5,γ=0.9,φ=5 000。
步骤2:生成初始状态S0。
步骤3:根据当前状态Sn−1,从可选择的动作集合An中,按式(7)选择动作αn。
步骤4:根据动作αn将状态更新为Sn,并计算累积奖励RSn−1,αn,按式(6)更新Q值。
步骤5:判断Sn是否为目标状态,是则执行步骤6,否则执行3。
步骤6:判断累加Q值是否已经收敛,是则执行步骤7,表示此时智能体已学习充分,否则执行步骤2。
步骤7:退出循环并记录数据,结束算法学习,求解得到最优调车作业计划。
4 算例分析
4.1 计算过程
采用上文模型和算法进行算例分析,使用的实验运行环境为:设备CPU-Intel Core i7,工具Vi⁃sual Studio(C#)。
以上文待编车列“34172612537”为例,在可用股道数量为3条时(K=3),强化学习模型进行充分学习后,累加Q值的变化如图2所示。起始阶段累加Q值为零,并且智能体会有较大概率进行探索,学习各种方案;随着迭代次数的增加,累加Q值会不断增加,而当智能体学习充分后,会执行回报最大的动作序列,使得累加Q值趋于稳定,达到收敛状态。
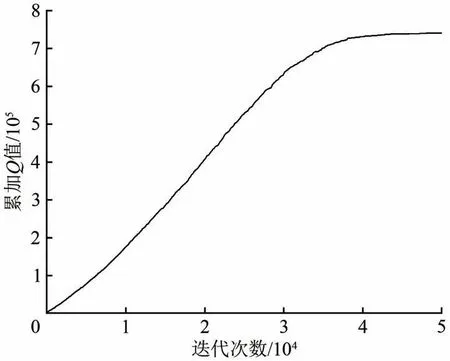
图2 累加Q值的变化
智能体学习充分后的最优调车表见表3,此时目标状态为s11=(1,1,2,3,3,3,2,2,1,2,2)。当到达目标状态后,智能体依照车辆重组流程,根据下落方案将车组依次溜放至相应股道上。由表3可知:待编车列的端组为车组7,其相邻位置为车组3,因此车组3 与7 均不溜放,连挂于调车机车上;车组下落结束后,根据车辆重组流程在调车表中依次寻找满足挂车条件1—3的车组;股道3为目标暂合列,该列第2 个车组及其右端相连的车组满足条件2,因此将车组2 与6 连挂至调车机车,此时,调车机车上所有车组(2637)并不构成接连,应根据摘车条件4—5 寻找能够溜放的股道;股道2中第3 个车组满足条件4,因此将Z=2 溜放至股道2,此时调车机车上所有车组仍不构成接连,须继续根据条件4—5 寻找能够溜放的股道,直至调车机车上所有车组构成接连且股道中没有比Z更大的车组,因此将Z=6溜放至股道1,Z=3溜放至股道2;此时仅剩端组7 连挂在调车机车上,且股道中没有比7更大的车组,因此须再次寻找满足挂车条件1—3的车组,直至股道中没有任何车组。

表3 最优调车表
表3执行的具体调车作业计划见表4。由表4可知:该方案共用到调车钩12 个,其中挂车钩5个,摘车钩7个;用到调车程17个。
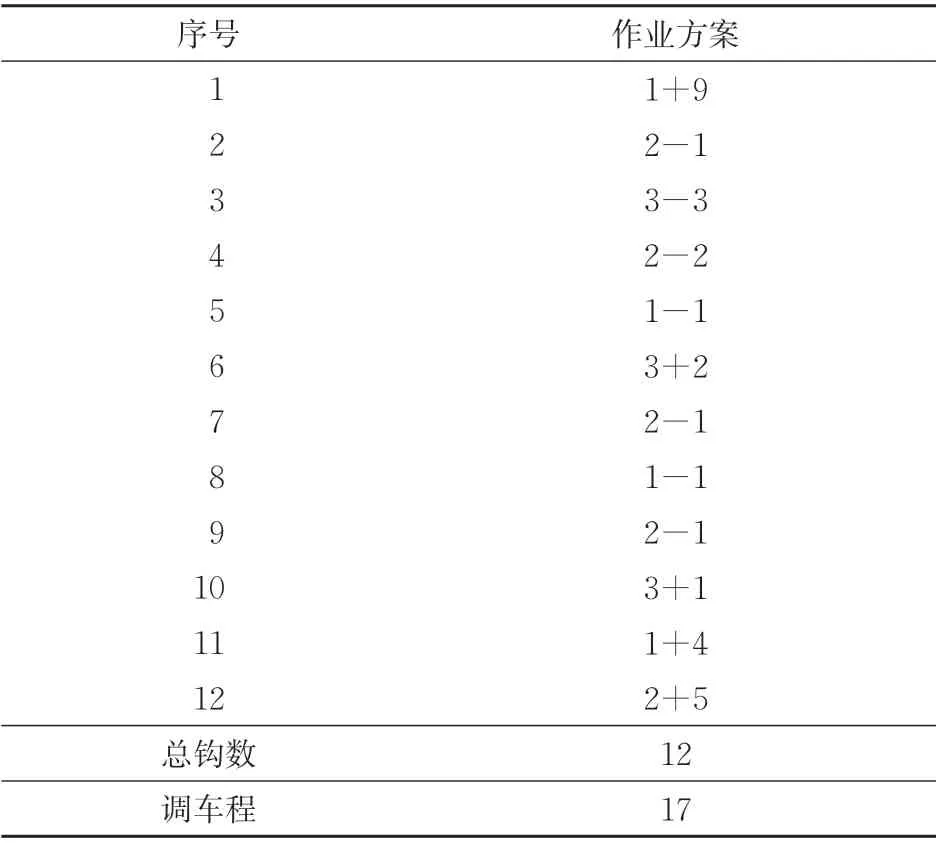
表4 调车作业计划表
4.2 效果对比
选取待编车列“34172612537”为案例1,待编车列“42531244627756186”为案例2,待编车列“1543253213”为案例3,分别利用统筹对口法、排序二叉树法和分支定界法,依次与本文方法进行调车作业计划的对比验证,结果见表5。对于案例1 中的统筹对口调车法在K=4 时存在多种优化方案,本文任选1 种进行对比;案例2 和案例3中的待编车列及所用方法得到的结果,分别取自文献[7]和文献[9]。
由表5可得出以下结论。

表5 本文方法与其他方法得到的调车作业计划表对比
(1)对比分析案例1 和案例2 结果,可以看出本文方法能在使用更少股道数量情况下得到优于统筹对口法及排序二叉树算法的调车作业计划。
(2)案例3 结果体现出,在相似设备及工具条件下进行仿真计算,本文方法求解得到的调车作业计划质量近似于消逆规则的分支定界法,且用时仅为53 s,远远短于后者的求解时间1 076 s[9]。
5 结 语
本文在结合表格调车法、强化学习技术和Q学习算法的基础上提出1种摘挂列车编组调车作业计划优化方法。将调车作业划分为下落和重组2 部分,通过动作、状态和奖励3要素建立了调车作业问题的强化学习模型,从而使摘挂列车编组调车作业优化问题转化为对下落方案的寻优问题。为求解该模型,改进Q学习算法,以最小化调车程为目标建立起待编车列与最优调车作业计划之间的映射关系,智能体学习充分、即累加Q值达到收敛状态时,即可得到最优的调车表及相应的调车作业计划。3 组算例分析验证了本文方法的合理性和有效性,相较于统筹对口法和排序二叉树法,本文方法使用的股道数量更少、调车作业计划更优;相较于分支定界法,本文方法可在更短时间内求解出质量近似的调车作业计划。这证实了本文方法有助于提高车站调车作业计划编制的智能化决策水平。
