飞翼式水下滑翔机的性能分析与控制策略优化

李志超， 乔岳坤

(1.哈尔滨工程大学 经济管理学院，黑龙江 哈尔滨 150001； 2.哈尔滨工程大学 水下机器人技术国家重点实验室，黑龙江 哈尔滨 150001)

水下滑翔机是一种以重浮力之差为驱动力的水下航行器。其最初的设计构想源于一种用于监测海洋剖面环境的水下浮体。为进一步扩大其监测的海洋区域，科研人员对其进行系统整合与优化，形成如今大家所熟悉的水下滑翔机。低成本、低功耗和长航程的特点极大地推动了水下滑翔机的应用与研究，使得水下滑翔机的发展呈现出多样化趋势。目前，水下滑翔机已经被广泛地应用于海洋研究和海洋环境监测，根据外形的结构形式可以大致划分为以下3类：常规鱼雷型、带螺旋桨的混合推进型以及翼身融合(飞翼)构型[1]。其中，飞翼式水下滑翔机具备高滑翔比的运动特性，吸引了大量研究人员的关注[2]。然而，目前关于飞翼式水下滑翔机性能分析与运动控制的研究成果并不多。鉴于此，本文将分析滑翔性能与系统设计参数之间的关系，并讨论垂直面的运动控制问题。

在水下滑翔机的动力学建模与运动控制方面，Leonard等[3]做出了巨大的贡献：首先利用牛顿-欧拉方程构建水下滑翔机的动力学模型；在此基础上，推导了水下滑翔机垂直面运动的稳态与设计参数的关系，预报其运动性能，并将分析结果应用于系统参数辨识；此外，利用二次最优控制方法(LQR)设计滑翔机垂直面运动的控制器，并分析闭环控制系统的稳定性问题。Leonard等[4]进一步研究了水下滑翔机的编队协同作业与运动控制问题，为水下滑翔机的编队控制和采样路径规划等实际工程问题提供了理论方案，并通过海上实验验证该理论方案的可行性。Bhatta等[5]利用奇异摄动理论对水下滑翔机的垂直面运动进行控制设计与稳定性分析。Kraus[6]将最优控制算法引入到水下滑翔机的垂直面运动控制与分析，把水下滑翔机的潜浮切换控制问题转换成一个基于Hamilton函数方程的两点边值问题，从而得到最优的控制序列，并通过仿真实验验证该控制器。此外，Woolsey等[7-8]利用摄动理论对水下滑翔机的路径规划、控制算法开展了研究。

国内对水下滑翔机动力学与控制理论的研究逐渐深入。王延辉[9]利用吉布斯—阿佩尔方程建立动力学模型，并在此基础上分析温差能水下滑翔机的空间与垂直剖面的运动性能，进一步设计LQR控制器，保证系统在参数不确定条件下的H∞鲁棒稳定性。俞建成等[10]基于水下滑翔机的动力学模型，利用回归算法分析其稳态滑翔运动，推导出空间螺旋运动的近似表达形式。张少伟等[11]对“海翼”号水下滑翔机的运动控制问题进行了深入的研究：1)首先通过系统分析给出水下滑翔机垂直面运动状态与系统控制输入之间的关系；2)其次利用最优控制算法设计运动控制器，并比较闭环控制系统在不同权重函数条件的状态响应；3)最后基于浮力调节速率不变的实际条件，给出系统控制的最优控制量。

目前，国内外科研人员对常规型水下滑翔机的动力学分析与运动控制问题展开了广泛且深入的研究。关于水下滑翔机性能分析的针对性报告指出，翼身融合结构的滑翔机具有更高的滑翔效率。但飞翼式水下滑翔机的机身前后不对称特征明显，相应的水动力影响难以忽略。动力学行为的差异导致相关的分析与研究不可或缺。自2003年以来，美国船舶物理实验室和华盛顿大学应用物理实验室已经对飞翼式水下滑翔机展开了全面的理论与实验研究。其公开的理论和实验研究成果均验证了飞翼式水下滑翔机优越的滑翔性能。从早期用于验证滑翔效率的Stingray，到后期应用于海洋监测的XRay1、改型XRay2和ZRay[12]，其工程技术渐趋成熟。但飞翼式水下滑翔机的发展却依然面临许多有待解决的难题，例如容易水翼失速和运动稳定性差等，对系统控制要求高。目前，国内相关研究还处于基础阶段，缺乏飞翼式水下滑翔机的动力学性能分析和运动控制方面的研究成果与参考资料，距离实用还有很大的距离。因此，本文将结合理论分析与实际水池试验对飞翼式水下滑翔机垂直面运动的性能分析和控制策略展开研究。

1 建模与稳态性能分析

本文首先建立如图1所示的坐标系,然后利用牛顿-欧拉方程构建飞翼式滑翔机垂直面运动的动力学方程，并以此为基础分析并预报其滑翔性能。

1.1 动力学方程建立

为了方便描述飞翼式水下滑翔机的空间运动，首先定义系统的运动状态量和动力学参数，如表1。

表1 动力学参数定义表

文献[13]，惯性系和随体坐标系如图1所示。其中，惯性系E-ζηζ相对地球静止，其原点位于地球某处；随体坐标系O-xyz则固定在水下滑翔机上，其原点与水下滑翔机的浮心一致。

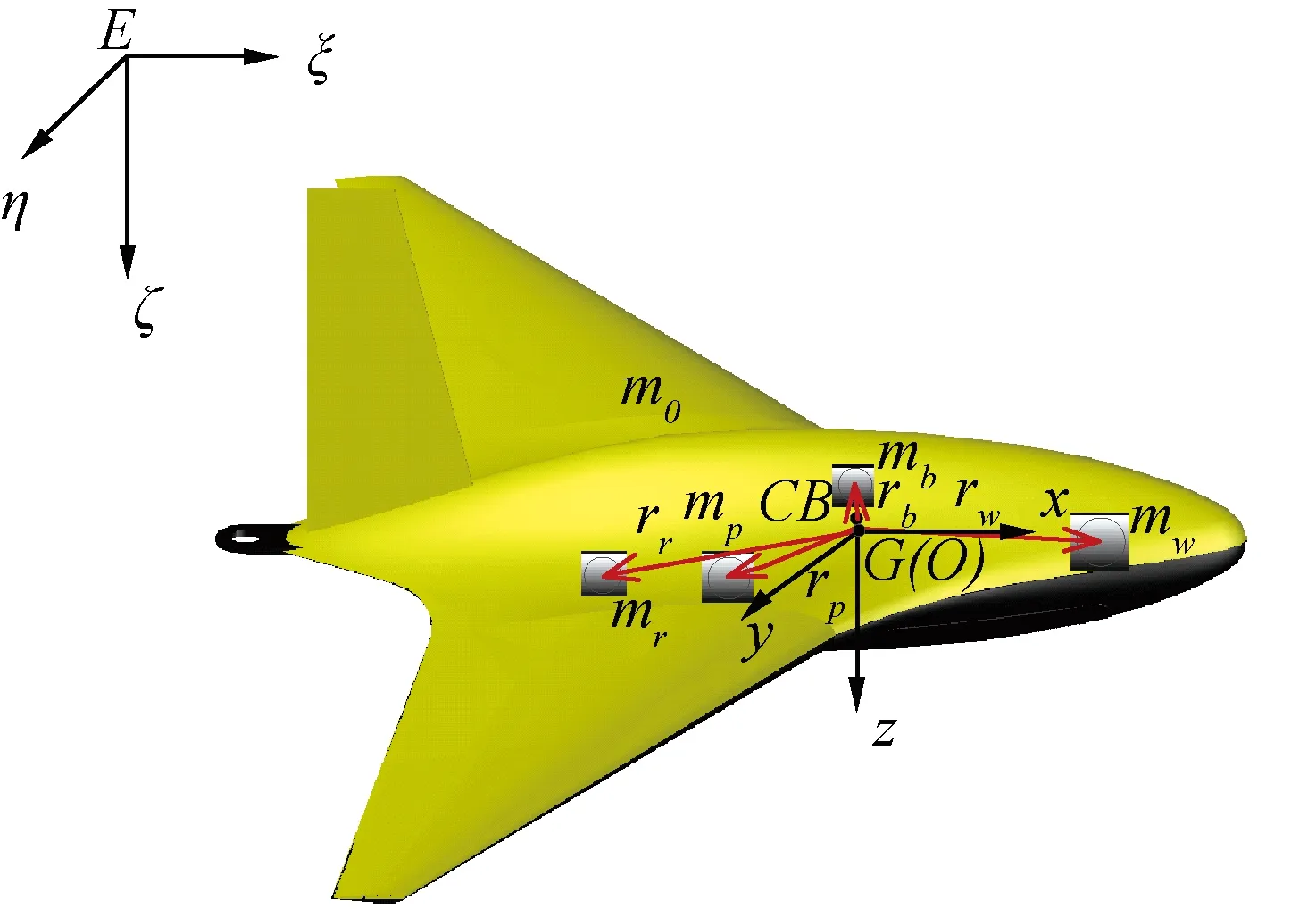
图1 坐标系建立

上浮和下潜过程中的受力分析如图2所示。

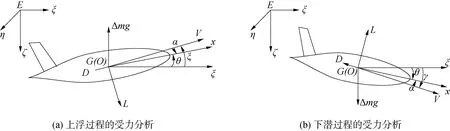
图2 上浮下潜的受力形式

根据牛顿-欧拉方程可得：

(1)

从而得到垂直面动力学方程：

(2)

式中：V0=[uvw]T，ω=[pqr]T。其中，u、v、w表示随体坐标系下的线速度；p、q、r表示随体坐标系下的转动角速度。

根据作用力和作用力矩的具体表达形式，方程(2)可以写为：

(3)

式中:D、L、MDL2分别表示水下滑翔机在运动过程中受到的阻力、升力和纵倾力矩。它们可以写成：

本文的研究基于一个飞翼式水下滑翔机样机，长1.6 m，翼展3 m，其净浮力调节范围为[-1.5 kg,1.5 kg]；重物滑块质量3 kg，滑块移动行程为180 mm，水平零浮力稳态下的滑块处于可移动行程的中间位置。

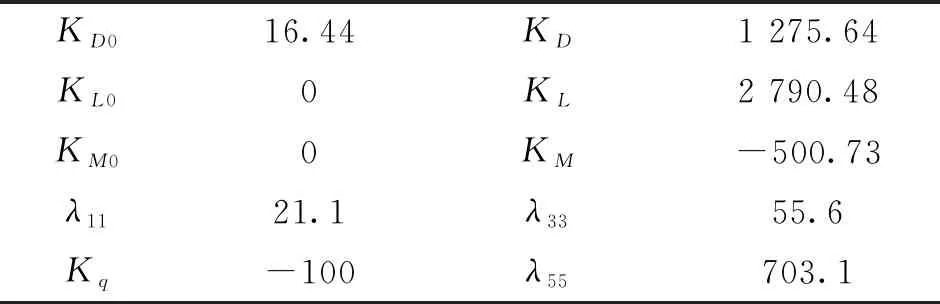
表2 系统模型参数

1.2 稳态性能分析

根据稳态条件：加速度及角加速度均为零，得:

(4)

设定姿态调节系统和浮力调节系统的输入参数，求解方程(4)可得系统的稳态值，从而得出飞翼式水下滑翔机的稳态滑翔性能。所得到的纵倾角、滑翔角以及滑翔比如图3所示。

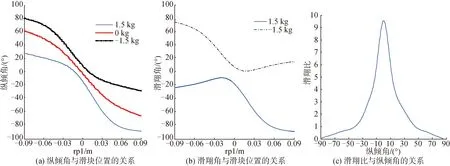
图3 纵倾角、滑翔角和滑翔比的性能范围

图3(a)和(b)预报了滑翔机在上浮和下潜过程中纵倾角和滑翔角与移动滑块的纵向位置之间的关系。虽然飞翼式水下滑翔机上下大致对称，但图3(a)和(b)都表明滑翔机上浮下潜的运动特性的不具备几何对称性，这主要是由浮力调节系统前置所导致的纵倾力矩造成。结合图3(a)和(b)的分析结果，图3(c)给出了滑翔比与纵倾角的关系，从中可以看出该飞翼式水下滑翔机在纵倾角0°附近取得最大滑翔比9.6∶1。需要强调的是，高滑翔比的容许区间较小，若定义8∶1及以上为高滑翔比，理想的纵倾角应为-7°～7°。综上所述，本文所研究的飞翼式水下滑翔机的运动调节范围如表3。

表3 滑翔运动的调节范围

图4 速度的性能范围

由图4(a)可以得知，在下潜运动过程中，滑翔速度随着滑块的纵向位置的增大而增大，并在滑块最大位置处取得最大值0.943 m/s；同时在上浮运动过程中，滑翔速度随着滑块的纵向位置的减小而增大，并在滑块最小位置处取得最大值0.934 m/s。从图4(b)所示结果可以看出：在下潜的过程中，垂直速度随着纵倾角的减小而增大；在上浮的过程，垂直速度则随着纵倾角的增大而增大。此外，下潜与上浮过程中水平速度均先随着纵倾角绝对值的增大而增大，在纵倾角±38°处取得最大值0.586 m/s，而后随着纵倾角绝对值的增大而减小。

2 控制器设计

本文研究的水下滑翔机可以通过移动滑块，改变系统重心位置，达到调节纵倾角的控制效果。针对飞翼式水下滑翔机运动稳定性要求高的特点，本节结合跟踪微分控制技术和模糊PID控制技术，提出一种跟踪微分模糊PID控制器，其结构如图5所示。其中，控制输入为期望纵倾角，控制输出为当前纵倾角，执行机构为滑块位置调节装置。控制流程大致如下：首先，跟踪微分器(TD)根据系统输入的期望状态安排指令信号的平滑过渡；其次，模糊控制策略根据指令信号进行模糊推理和PID参数整定；最后，PID控制器进行运动控制，实现稳定的状态切换，避免出现水翼失速等危险情况。

图5 系统控制结构

根据文献[14-15]，跟踪微分器的离散模式具体可以表示为：

(5)

(6)

对a，d等中间参量进行说明，有：

(7)

为了验证本文提出的跟踪微分模糊PID控制器，下面展开仿真实验研究。

仿真实验1：在不进行浮力调节的情况下，滑翔机在水平位移100 m处进行纵倾角切换，从当前状态-20°切换到期望值-5°。仿真结果如图6和图7所示。

图6对比了纵倾角切换过程中跟踪微分模糊PID控制器和模糊PID控制器的控制效果。图6(a)中的轨迹差异由2种控制器的差异造成。从中可以看出，模糊PID控制器的响应快速，轨迹存在较为明显的折角；而跟踪微分模糊PID控制器响应较慢，轨迹过渡平滑。图6(b)给出了2种不同控制器的纵倾角切换响应对比。其中，模糊PID控制器早期响应速度快，但后期的收敛速度较慢；而跟踪微分模糊PID控制器的响应速度具有较好的均衡性。两者均无明显的超调，控制效果良好。

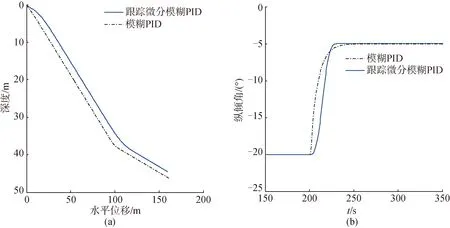
图6 仿真实验1的运动轨迹和纵倾角响应曲线

从图7可以看出两者之间的巨大区别：模糊PID控制器的输入响应(滑块纵向位置的变化)迅速，但存在明显的振荡效应并且振幅较大；而跟踪微分模糊PID控制器的输入响应较慢，但过渡平缓，无剧烈的振荡现象。两者都可以实现对纵倾角切换的良好控制。但对于稳定性要求高的飞翼式水下滑翔机而言，跟踪微分模糊PID控制器更合适。

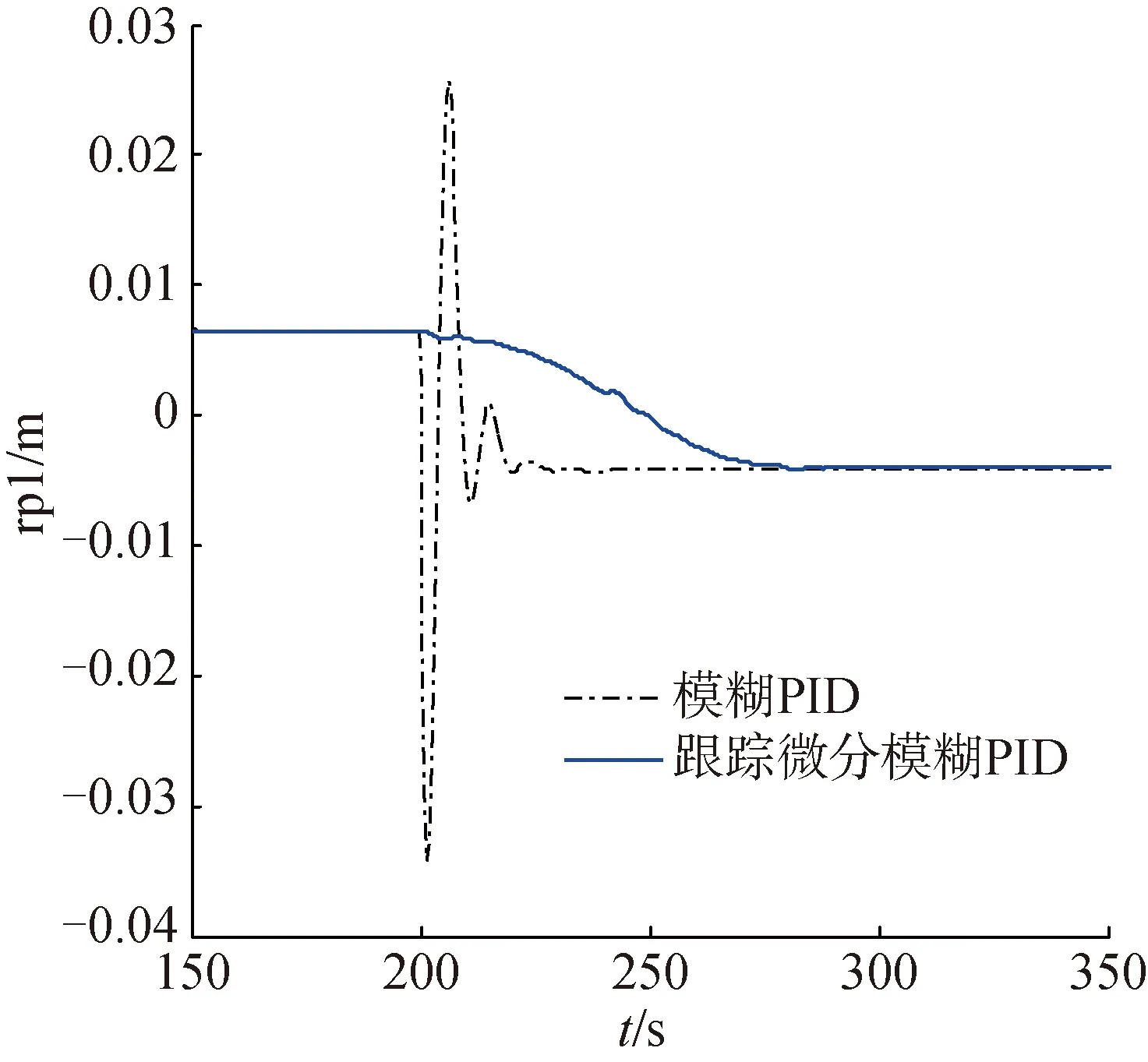
图7 仿真实验1的滑块位置响应曲线

仿真实验2：在浮力调节速率恒定的条件下进行潜浮切换，将净浮力从-1.5 kg调节到1.5 kg，同时将纵倾角从-10°调节到10°。仿真结果如图8和图9所示。

图8对比了潜浮切换过程中跟踪微分模糊PID控制器和模糊PID控制器的控制效果。从中可以看出，由于跟踪微分器的安排过渡过程，滑翔轨迹和纵倾角的切换响应更加平滑。图9给出了以上2种控制器的控制输入量(即移动滑块的纵向位置)的对比。可以得知，模糊PID控制器的输入响应迅速且存在明显的振荡效应，需要消耗较多的系统能源；跟踪微分模糊PID控制器的输入响应则相对缓慢而平滑，调节量明显较前者少。同时，在实际的工程应用当中，滑块的移动速度受限，快速的响应不易实现。因此，跟踪微分模糊PID控制器更加适合于现实的工程应用。

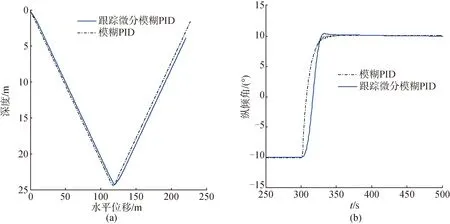
图8 仿真实验2的运动轨迹和纵倾角响应曲线

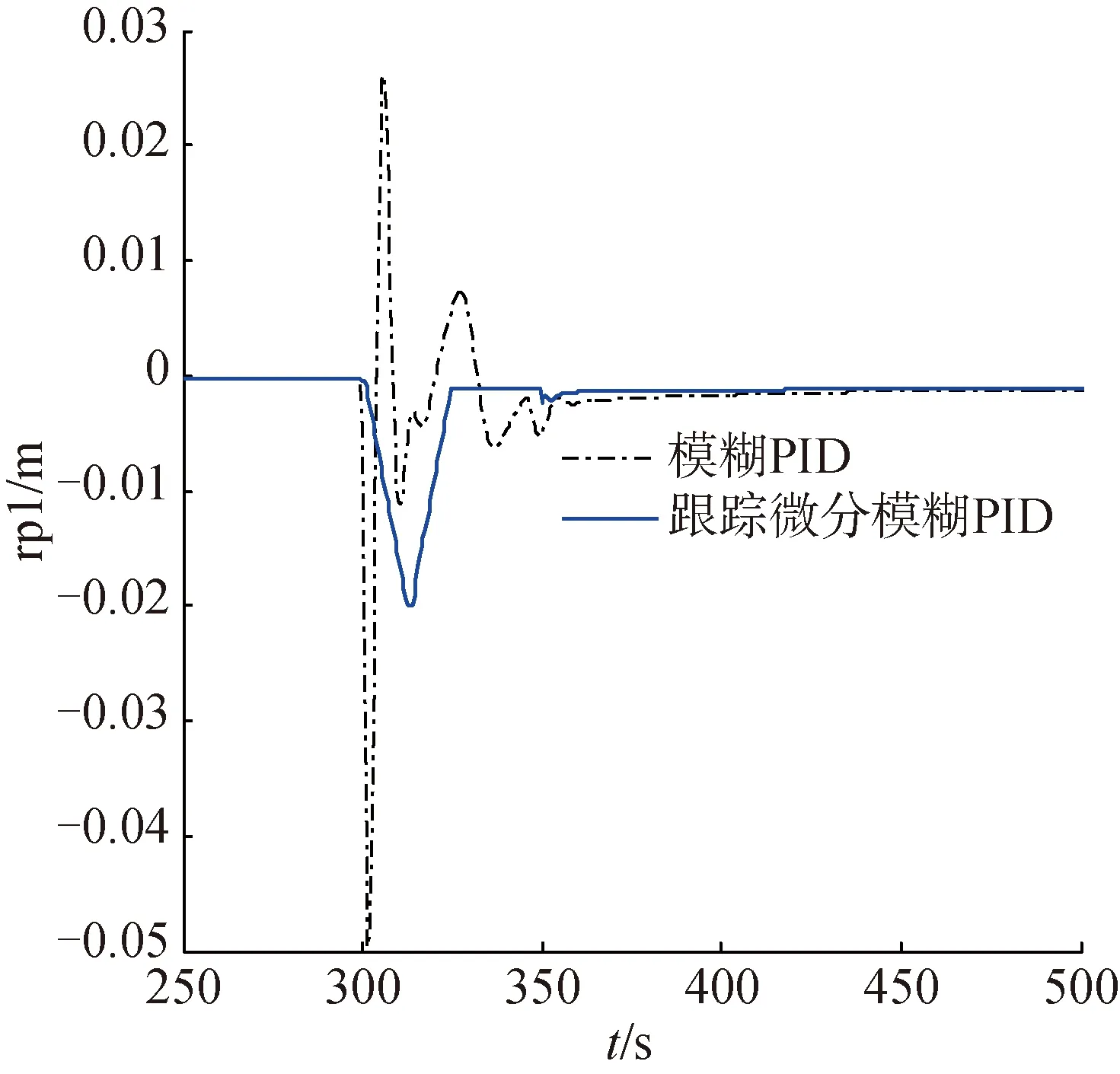
图9 仿真实验2的滑块位置响应曲线

3 水池试验验证

本文将通过水池实验验证性能分析的结果和所提出的跟踪微分模糊PID控制器。图10为试验过程的视频截图。水池实验包括了2部分：纵倾角跟踪和潜浮切换。

图10 试验过程视频截图

水池试验1：当滑翔机到达深度9 m后，浮力调节系统将净浮力从-1.5 kg调节到1.5 kg，同时姿态调节系统将纵倾角由-30°切换到期望值20°。水池试验的结果如图11所示。

图11(a)和(b)分别给出了飞翼式水下滑翔机深度和纵倾角随时间的变化。可以看出，滑翔机深度与纵倾角的切换过程光滑无振荡。试验结果有效地验证了本文所提出的控制器。

图11 水池试验1的控制效果

水池试验2：滑翔机以净浮力-1.5 kg，深度0.5 m，纵倾角0°，速度0 m/s的初始状态下潜，期望纵倾角为-6°；当到达深度5 m时，浮力调节系统将净浮力从-1.5 kg调节到1.5 kg，同时姿态调节系统将纵倾角从-6°调节到6°。水池试验结果如图12所示。

图12(a)和(b)分别给出了飞翼式水下滑翔机深度和纵倾角随时间的变化。在滑翔运动初期，由于初始速度为0，滑翔机埋艏加速，导致纵倾角突然变小。同时，由于深度传感器被安装在滑翔机的尾部，深度值也相应地变小。图中结果显示，深度和纵倾角的变化与理论分析一致。此外，滑翔机深度与纵倾角的切换过程较为光滑、无明显的振荡，控制效果良好。试验结果验证了本文所提控制器在高滑翔比条件下的有效性。

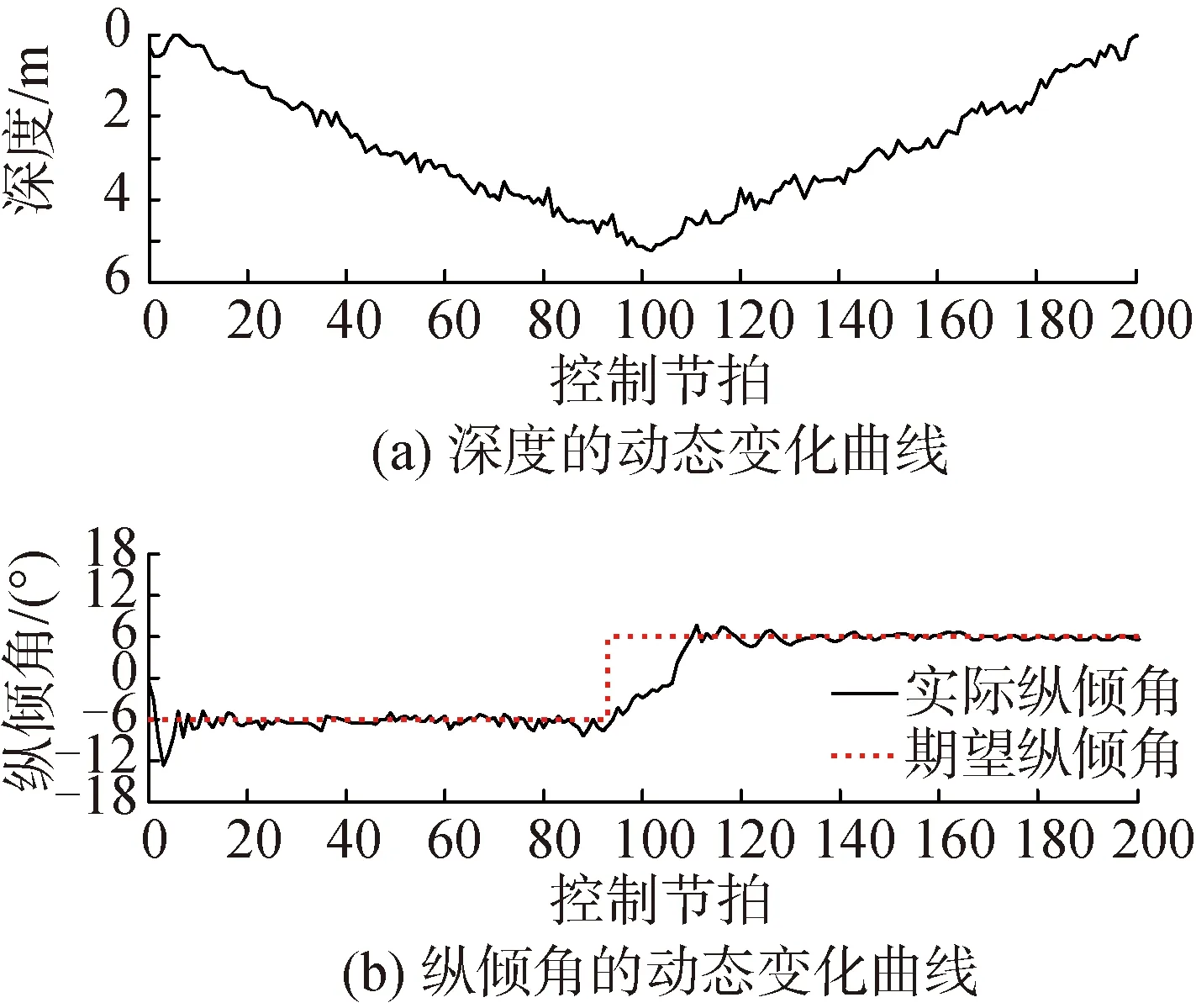
图12 水池试验2的控制效果

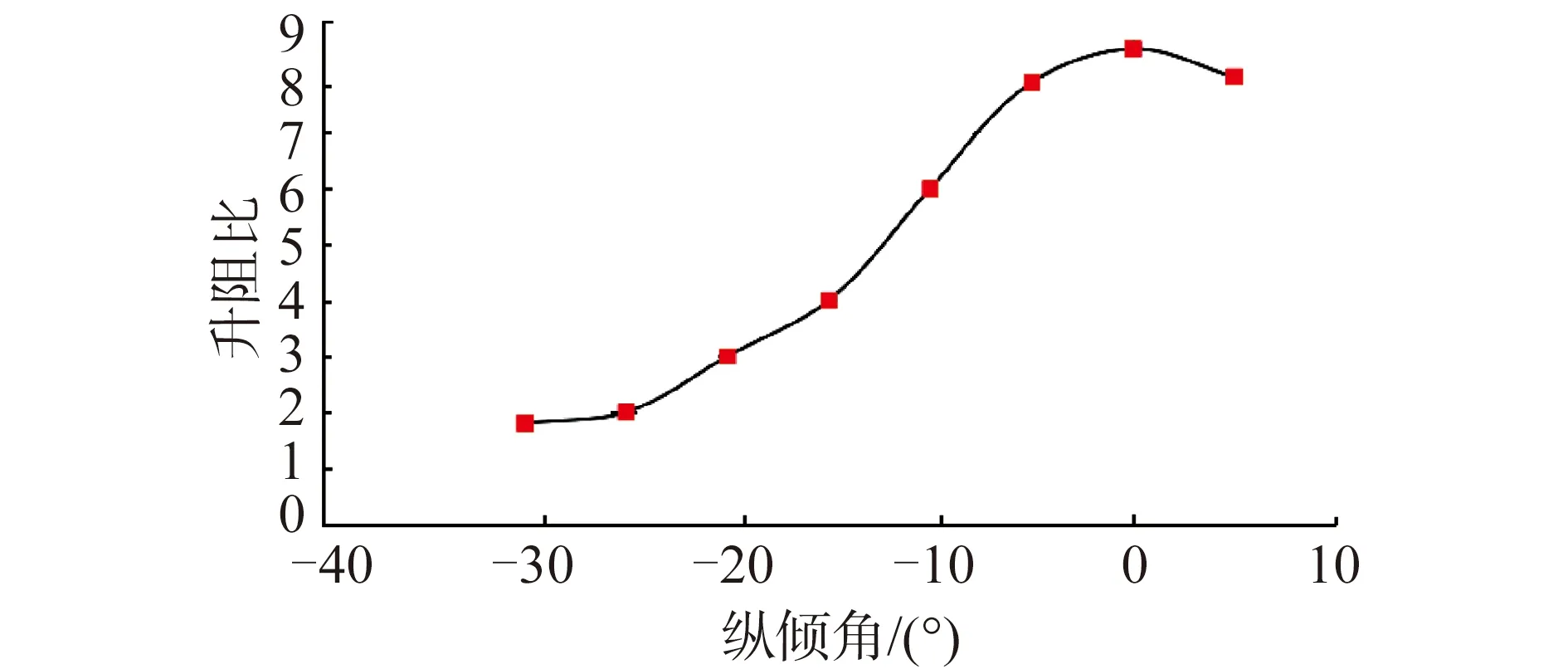
图13 升阻比

需要强调的一点是，尽管试验使用的飞翼式水下滑翔机样机没有装备位移传感器(例如惯导和DVL等)，没有位移信息的反馈，滑翔机的滑翔比依然可以通过水池的几何尺寸和收集到的深度信息估算得到。实验结果验证了飞翼式水下滑翔机大滑翔比的优势。

4 结论

1)从动力学分析中预报了飞翼式水下滑翔机的滑翔性能。结果显示其最大滑翔比可达9.6∶1，从理论上验证翼身融合水下滑翔机滑翔效率高的优势。

2)仿真结果从理论上验证了跟踪微分模糊PID控制器的有效性。

3)水池试验的结果证明了翼身融合水下滑翔机的大滑翔比优势，并验证了跟踪微分模糊PID控制器在实际工程应用当中的可行性。