约束条件下基于满意模型预测控制的动基座水下无人航行器对接控制
2022-02-16张伟伍文华滕延斌宫鹏唐业竞
张伟, 伍文华, 滕延斌, 宫鹏, 唐业竞
(1.哈尔滨工程大学 水下机器人技术重点实验室,黑龙江 哈尔滨 150001; 2.中国船舶科学研究中心 水动力学国防重点实验室,江苏 无锡 214082)
动基座水下无人航行器(unmanned underwater vehicles,UUV)回收是指UUV通过运动控制使得其最终保持与运动母船的位置和姿态一致[1-3],在动态过程中完成与母船的回收。动基座UUV回收过程主要包括跟踪控制阶段和对接控制阶段。在UUV的跟踪控制中,Rezazadegan等[4]研究了六自由度水下机器人的轨迹跟踪控制问题,基于李亚普诺夫直接法和反步技术,提出了一种自适应控制器,保证了对参数不确定性的鲁棒性。赵杰梅等[4]设计了神经网络自适应输出反馈控制器应用于AUV水平面路径跟踪,使得系统跟踪误差最终一致有界。王宏健等[5]设计了滤波反步法跟踪控制器应用于欠驱动UUV的三维轨迹跟踪控制,增强了系统对噪声的鲁棒性。张伟等[6]针对UUV在流体运动中存在时变干扰问题,提出了自适应RBF神经网络反步跟踪控制,提高了UUV对环境的自适应能力。王晓伟等[7]应用李雅普诺夫理论和反步法设计了滑模控制器,实现了欠驱动AUV对三维直线的跟踪控制,削弱了系统抖振。在UUV的对接控制中,张伟等[8]研究了UUV对水下坞舱的对接问题,提出了一种基于对线控位策略的灰色预测PID控制方法,取得了良好效果。郑荣等[9]研究了AUV与移动坞站的对接技术,提出了一种基于路径特征匹配的动态导引算法,通过试验验证了该导引算法的可靠性。Enrico等[10]将强化学习策略应用于AUV的对接控制,以更低的计算成本实现了最优控制的性能,对于不同系统具有较强的适应性。上述回收控制方法虽然在一定程度上取得了良好的效果,但由于算法本身的局限性而难以处理各种复杂约束。水下无人潜航器(UUV)作为一种水下无人自主化装备,被广泛应用于海洋调查、勘测、搜索等领域[1]。传统的UUV回收主要通过水面船起吊完成,这种过多依靠人力的回收方式存在隐秘性差、安全性低、受环境影响大等缺点[2]。因此,UUV水下自主回收对接技术日益成为水下无人系统领域的研究热点[3]。
由于模型预测控制对存在多种复杂约束,以及不确定性的系统具有良好的控制性能[11-12],因此本文将基于MPC控制设计动基座UUV对接控制器。然而,传统的MPC控制方法在对UUV数学模型进行目标函数优化时,不仅计算代价较高,而且其在约束条件下解算的全局最优解,可能存在以牺牲其他指标为代价的问题。满意控制却可以很好地解决这一问题。满意控制是把约束条件、代价函数当作广义上的要求,通过使用有限的操作变量去符合这些要求,它的解是根据这些要求的不同权衡得到的满意解[13]。基于以上讨论,本文提出了约束条件下基于满意MPC的动基座UUV对接控制方法,采用满意控制思想通过MPC控制方法对UUV模型进行分布式处理,将单一的UUV对接控制性能函数转化为多自由度多目标函数,从而对多个目标函数分别求得最优控制解,然后由这多个局部的最优控制解组成满足对接约束的全局次优解,也就是满意解,从而保证系统的鲁棒性与稳定性。
1 UUV回收对接系统与模型
1.1 UUV回收对接系统
本文所研究的回收对接系统是基于叉柱式的回收对接系统[14],该系统主要包括对接UUV与回收母船两大部分。如图1所示,对接UUV主要由对接柱、超短基线(USBL)接收机及水下摄像机组成。回收母船主要由母UUV、声学信标、L型光学灯阵、对接导引叉组成。首先,UUV通过声光组合的导引方式获取与回收母船的相对位置和姿态信息。然后,UUV通过运动控制器进行运动控制和姿态调整,从而不断缩小UUV与运动母船对接叉的位置和姿态误差。最后,UUV的对接柱沿运动母船上的导引叉滑动到中间的锁紧装置处,从而完成UUV与运动回收母船完成对接。
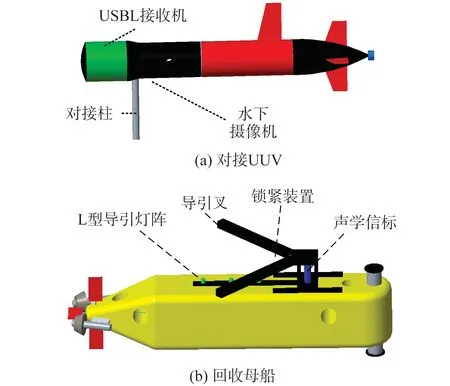
图1 UUV回收对接系统
1.2 对接UUV模型
为了研究上的方便,根据UUV的主要特征,现作出如下合理假设:
1)UUV重力与浮力大小基本相等;
2)UUV外形的断面、切面和截面是3个严格对称的对称面;
3)UUV在运动过程中横倾角很小,可以基本忽略。
基于以上假设,可建立UUV五自由度的动力学与运动学模型[15]:
(1)
(2)
其中:
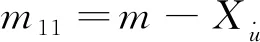
式中:m为UUV质量;τu、τv、τw和τr、τr分别表示UUV所受的控制力和力矩;ξ、η、ζ分别为UUV北向、东向、深度位置;φ、θ、Ψ分别为UUV的横摇角、纵摇角和艏向角;u、v、w分别为UUV的纵向、横向和垂向速度;p、q、r分别为UUV的横摇角、纵摇角、艏向角速度。

1.3 回收母船模型
在本文研究的动基座UUV对接控制中,运动回收母船采用的是另一条不同的UUV,因此运动回收母船的模型与对接UUV的空间五自由度模型(1)、(2)一致,在此处不再赘述。
回收母船主要参数形式如下:
位置和姿态向量为[ξmηmζmφmθmψm]T;速度和角速度向量为[umvmwmpmqmrm]T;控制量为[τmuτmvτmwτmpτmqτmr]T。
2 多种约束问题分析
在动基座UUV对接过程中,存在着各种复杂约束。本节从UUV回收对接安全性、UUV自身物理限制、UUV所受环境干扰力等角度出发,将多种约束问题主要归为状态约束、自身约束和干扰约束三大类。
2.1 状态约束
状态约束主要是对UUV的航向状态所做的约束,主要分为终端对接约束和速度约束。
1)终端对接约束。
终端对接约束主要是根据回收母船上的位置划定对接安全区域和禁止驶入区域,使得UUV在终端对接过程中处于相对安全的状态。动基座UUV终端对接安全区如图2所示。
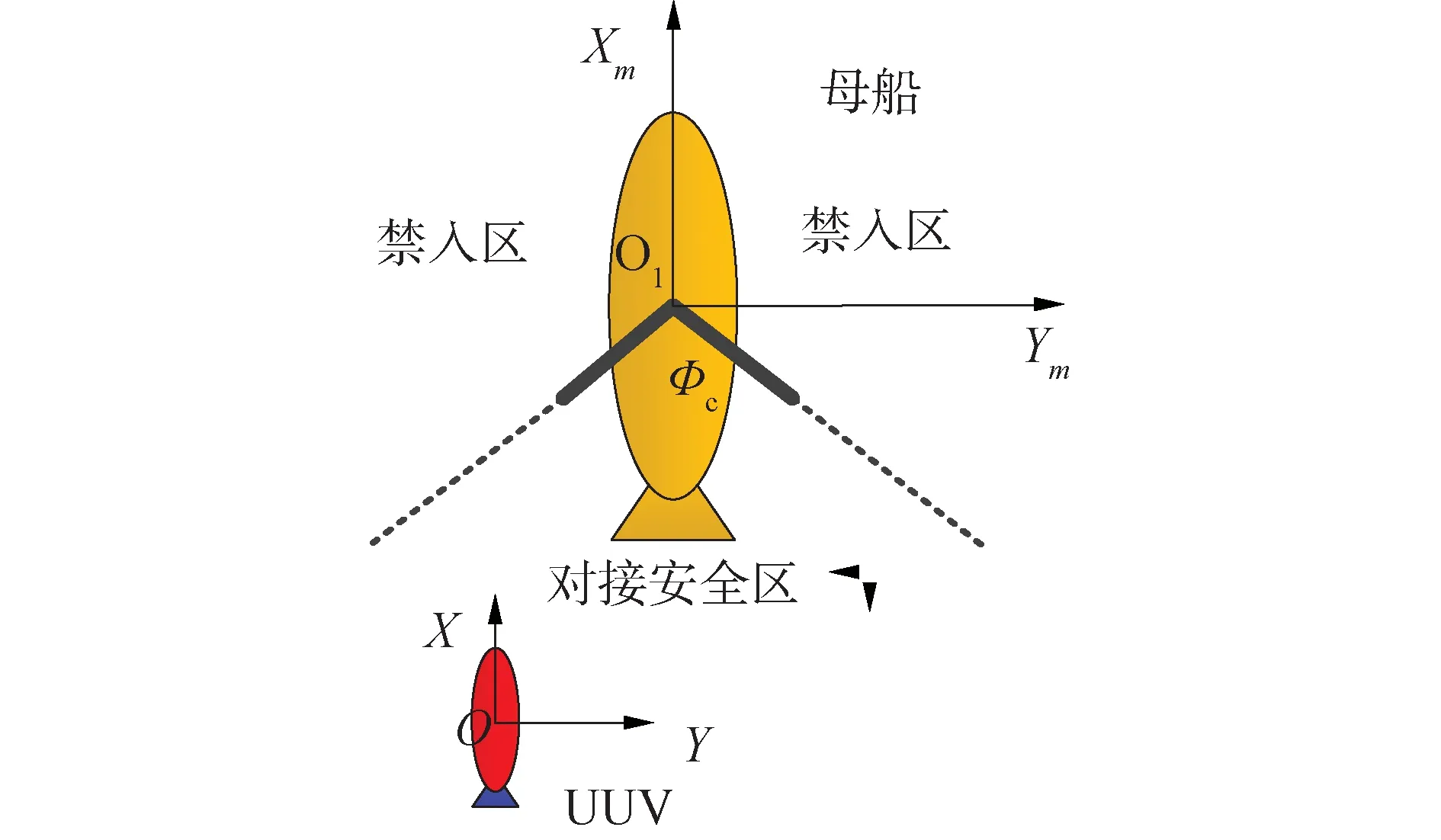
图2 动基座UUV终端对接安全区示意
通过将动基座UUV终端对接约束转化为位置约束,k时刻该约束条件可表示为:
(3)
式中:(x(k),y(k))为UUV的水平面位置坐标;(xm(k),ym(k))为运动回收母船的水平面位置坐标;Φc为对接导引叉的开角;Rd为考虑到UUV转向能力而设定的值。
在第k时刻,可将UUV运动坐标系下的约束(3),转化为大地坐标系下的约束:
(4)
式中:ξmin(k)、ηmin(k)、ζmin(k)分别为当前时刻3个输出量的最小值;ξmax(k)、ηmax(k)、ηmax(k)分别为当前时刻3个输出量的最大值。
2)速度约束。
速度约束主要是对UUV的速度增量进行约束,从而防止UUV因速度变化过快与运动回收母船发生碰撞,速度变化量约束表示为:
(5)
式中:u(k)、v(k)、w(k)是第k时刻的速度量;u(k-1)、v(k-1)、w(k-1)是k-1时刻的速度量;d·是根据UUV的速度变化而分别设定的值。
根据UUV动力学模型,速度变化量约束(5)可转化为控制力变化量约束:
(6)
式中:τ·(k)表示k时刻控制力;τ·(k-1)表示k-1时刻控制力;Δτ·表示控制量增量。
2.2 自身约束
自身约束是由于UUV本身硬件能力的限制,主要包括最大舵角约束和推进器推力约束,可将这2种约束整合,表示为控制量约束:
umin≤u(k)≤umax
(7)
式中u(k)=[τu(k)τv(k)τw(k)τq(k)τr(k)]T。
2.3 干扰约束
干扰约束即为动基座UUV在回收过程中所受到的干扰,主要包括海流约束和近壁面约束。
1)海流约束。
海流约束是指UUV在水下航行过程中所受到的定常海流干扰约束。假设海流大小为τcd,以及在固定坐标系下的方向为(φcd,θcd,ψcd),将其转换到运动坐标系下的干扰为:
(8)
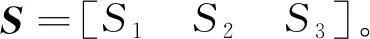
其中Si(i=1,2,3)具体形式为:
2)近壁面约束。
近壁面约束是指UUV靠近运动回收母船时所引起的流体的变化经过母船的反弹而对UUV的影响。根据文献[16],对接过程中UUV在近壁面干扰下所受的垂向力τjdw、纵倾力矩τjdq关系式为:
(9)
式中:ρ为流体密度;g为重力加速度;U为速度矢量;V为UUV排水体积;CZ、CM分别表示垂向力、纵倾力矩参数。
将式(8)、(9)整合得到对接过程中的控制干扰量约束为:
(10)
3 控制器设计
在UUV与运动回收母船对接的过程中,存在各种复杂约束,要求UUV在多自由度控制中完成与母船在一定精度内的对接。针对以上问题,本文提出了基于满意MPC的动基座UUV对接算法。首先,将UUV模型按照满意思想进行分布式处理,根据MPC 理论,构建UUV北东位置、深度、纵倾和航向预测模型;然后将动基座UUV对接过程存在的复杂约束分别应用到对应的预测模型中,设计相应的满意目标函数,对目标函数优化求解;最后将解算出的下一时刻控制量作用于UUV系统,从而进行反复解算,滚动优化直至完成UUV对运动回收母船的对接。
3.1 预测模型
1)构建UUV北东位置预测模型。
首先根据UUV五自由度运动学模型(1)、动力学模型(2),引入相应的干扰约束(10),构建UUV北东位置模型:
(11)
将式(11)表示成连续状态空间模型:
(12)


将模型(12)采用一阶差商的离散化方法离散化,采样周期为1,得到离散化后的模型为:
式中:A1p=A1p+I4×4;B1p=B1c;C1p=C1c。
然后,根据北东位置离散化模型(13)构建UUV北东位置误差增强模型:
(14)

最后将模型(14)在预测时域Np1和控制时域Nc1内展开,得到北东位置预测模型:
Y1=F1x1e(k)+Φ1(ΔU1+ΔDu1)
(15)
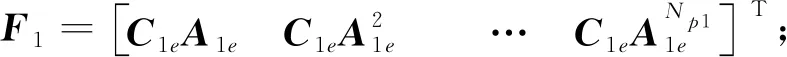
Y1=[y1e(k+1|k)y1e(k+2|k)…y1e(k+Np1|k)]T;
ΔDu1=[due1(k)due1(k+1) …due1(k+Nc1-1)]T;
ΔU1=[u1e(k)u1e(k+1)…u1e(k+Nc1-1)]T;
2)构建UUV深度预测模型。
根据UUV五自由度空间模型(1)、(2),引入干扰约束(10),构建UUV深度模型:
(16)
同样地,可得到UUV深度误差增强模型:
(17)
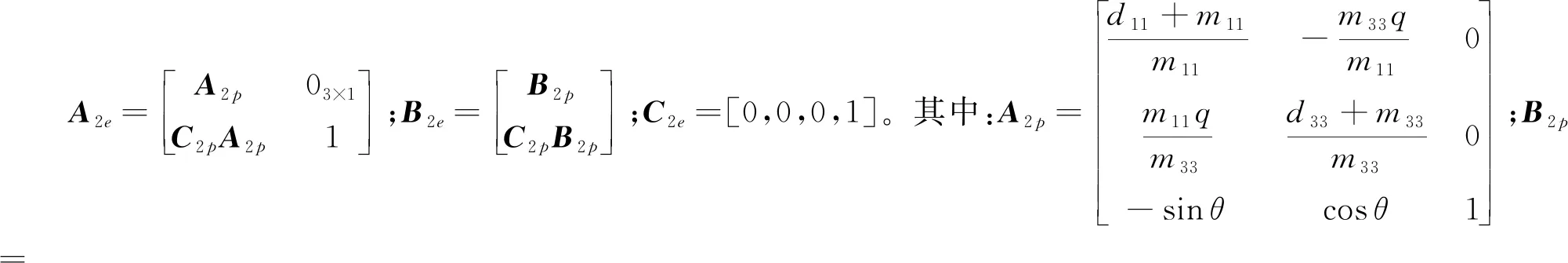
将模型(17)在预测时域Np2和控制时域Nc2内展开,得到深度预测模型:
Y2=F2x2e(k)+Φ2(ΔU2+ΔDu2)
(18)
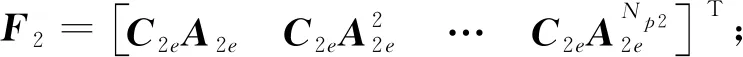
Y2=[y2e(k+1|k)y2e(k+2|k)…y2e(k+Np2|k)]T;
ΔDu2=[due2(k)due2(k+1)…due2(k+Nc2-1)]T;
ΔU2=[u2e(k)u2e(k+1)…u2e(k+Nc2-1)]T;
3)构建UUV纵倾预测模型。
根据UUV五自由度空间模型(1)、(2),干扰约束(10),构建UUV深度模型:
(19)
同样地,可得到UUV深度误差增强模型:
(20)

将模型(20)在预测时域Np3和控制时域Nc3内展开,得到纵倾预测模型:
Y3=F3x3e(k)+Φ3(ΔU3+ΔDu3)
(21)

Y3=[y3e(k+1|k)y3e(k+2|k)…y3e(k+Np3|k)]T;
ΔDu3=[due3(k)due3(k+1)…due3(k+Nc3-1)]T;
ΔU3=[u3e(k)u3e(k+1)…u3e(k+Nc3-1)]T;
4)构建UUV航向预测模型。
根据UUV五自由度空间模型(1)、(2),构建UUV航向模型:
(22)
同样地,可得到UUV航向误差增强模型:
(23)
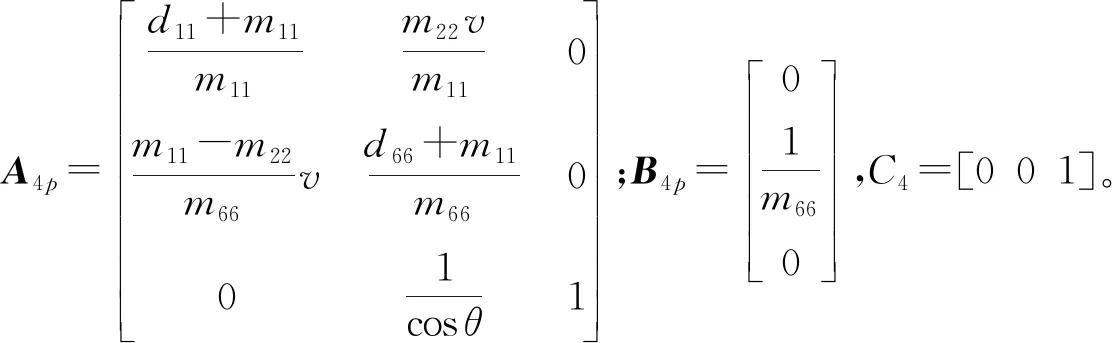
将模型(23)在预测时域Np4和控制时域Nc4内展开,得到航向预测模型:
Y4=F4x4e(k)+Φ4ΔU4
(24)
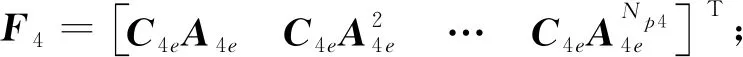
Y4=[y4e(k+1|k)y4e(k+2|k)…y4e(k+Np4|k)]T;
ΔU4=[u4e(k)u4e(k+1)…u4e(k+Nc4-1)]T;
3.2 约束处理与目标函数优化求解
1)北东位置预测模型约束处理与优化求解。
根据终端对接约束(4),提取相应的大地坐标系下北东位置约束,可得到预测时域内的北东位置终端对接约束:
Y1min≤Y1≤Y1max
(25)
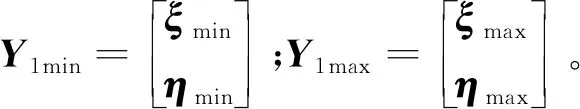
将北东预测模型(15)代入式(25)的约束条件中,得到:
Y1min≤F1x1e(k)+Φ1(ΔU1+ΔDu1)≤Y1max
(26)
根据速度约束(6),提取相关速度约束,可得到控制时域内的北东位置速度约束:
ΔU1min≤ΔU1≤ΔU1max
(27)
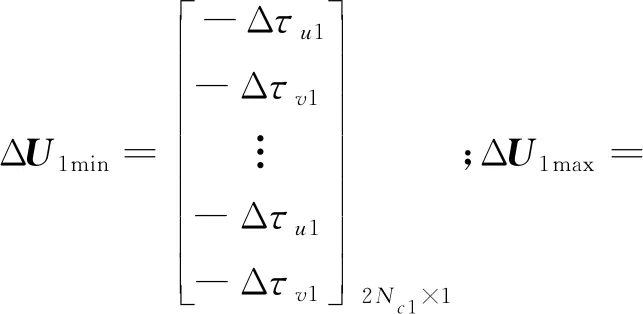
根据UUV自身约束式(7),可得到控制时域内的UUV北东位置自身约束:
(28)
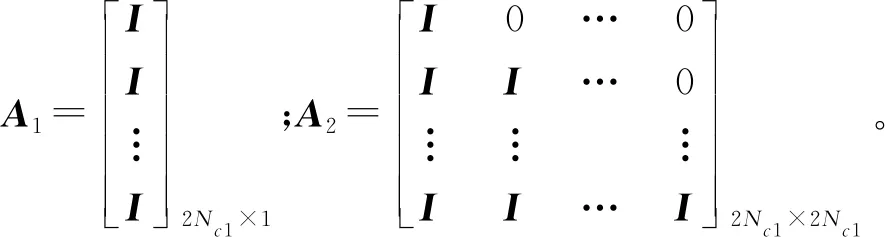
基于以上分析,综合约束条件式(26)、式(27)、式(28),可以得到UUV对接北东位置约束条件:
(29)
设计北东位置目标函数为:
minJ1=(Y1d-Y1)T(Y1d-Y1)+ΔU1TRw1ΔU1
(30)
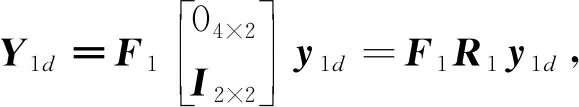
求得的控制量变化量为:
那么,得到北东位置控制量的增量为:
(32)
2)深度预测模型约束处理与优化求解。
根据UUV终端对接约束(4),提取相应的深度约束,可得到预测时域内的深度终端对接约束:
Y2min≤Y2≤Y2max
(33)
式中:Y2min=ζmin;Y2max=ζmax。
将深度预测模型(18)代入式(33)的约束条件中,得到:
Y2min≤F2x2e(k)+Φ2(ΔU2+ΔDu2)≤Y2max
(34)
根据式(6)所示的碰撞约束,得到控制时域内的纵倾碰撞约束:
ΔU2min≤ΔU2≤ΔU2max
(35)

根据UUV自身约束(7),将其在控制时域内展开,可得到控制时域内的UUV深度自身约束:
(36)
式中:A21、A22与式(28)相同,仅维数不同,A21维数为Nc2×1,A22维数为Nc2×Nc2。
综合约束条件式(26)、(27)、(28),可得到UUV对接深度约束条件:
(37)
下一步,设计深度目标函数为:
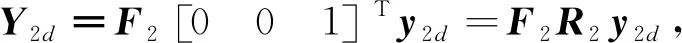
求得的控制量变化量为:
那么,得到深度控制量的增量为:
Δu2(k+1)=Δτw(k+1)=ΔU2(1)
(40)
3)纵倾预测模型约束处理与优化求解。
根据UUV自身约束式(7),将其在控制时域内展开,得到控制时域内的UUV纵倾自身约束:
(41)
式中:A31、A32与式(28)相同,仅维数不同,A31维数为Nc3×1,A33维数为Nc3×Nc3。
设计纵倾目标函数为:
(42)
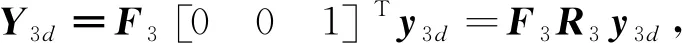
求得的控制量变化量为:
那么,得到深度控制量的增量为:
Δu3(k+1)=Δτq(k+1)=ΔU3(1)
(44)
4)航向预测模型约束处理与优化求解。
根据UUV自身约束式(7),将其在控制时域内展开,得到控制时域内的UUV航向自身约束:
(45)
式中:A41、A42与式(28)相同,仅维数不同,A41维数为Nc4×1,A42维数为Nc4×Nc4。
下一步,设计航向目标函数为:
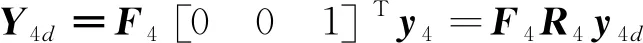
求得的控制量变化量为:
那么,得到航向控制量的增量为:
Δu4(k+1)=Δτr(k+1)=ΔU4(1)
(48)
3.3 滚动时域控制
基于上节讨论,得出了不同预测模型、不同目标函数下求解的控制量增量式(32)、(40)、(44)和(48)。由此,可得UUV下一时刻的控制量:
(49)
将u(k+1)作为实际的控制输入量作用于UUV系统,得出UUV在k+1时刻的状态量,然后通过约束条件下满意MPC控制算法,继续解算出第k+2时刻的控制量u(k+2),如此循环迭代求解UUV输入控制量,直至完成动基座UUV对接控制。
4 仿真结果与分析
在动基座UUV对接的仿真过程中,回收母船做定深圆周运动。母船的初始速度为[umvmwmqmrm]=[0.3 0.05 0 0 -0.0157],位姿状态为[ξmηmζmθmψm]=[45.6 -23.8 12.49 0 -4.646],初始控制力与力矩为[τmuτmvτmwτmqτmr]=[30 5 0 0 0],对接UUV的初始速度为[uvwqr]=[0.27 0.155 0 0 -0.0157],初始位姿状态为[ξηζθψ]=[48-319.50-4.59],UUV初始控制力与力矩为[τuτvτwτqτr]=[27.4 19.4 0 0 1.32]。海流干扰力大小为8 N,仿真时间为500 s。本次仿真对比了在约束条件下,UUV动基座对接过程中满意MPC和MPC之间的差异,并给出了相应的分析。
UUV三维运动轨迹如图3所示,UUV初始位置距离母船较远。约束条件下MPC控制的UUV经过较大的波动后才收敛到达回收母船运动轨迹;约束条件下满意MPC控制的UUV轨迹平滑,并且UUV深度一直处于母船的上方,这就保证了UUV能够稳定获取运动回收母船上对接装置的声学信号。
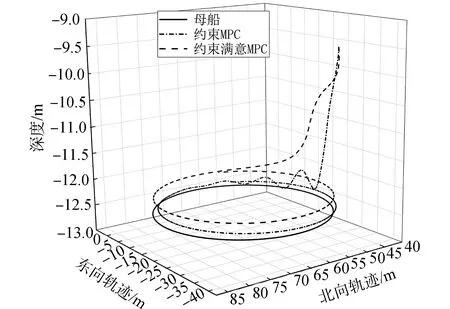
图3 UUV三维轨迹对比图
从图4(a)的纵向误差对比图中可以看出,满意MPC比MPC能够更快地达到稳定状态,并且误差更小;从图4(b)横向误差对比图中可以看出,满意MPC比MPC下UUV与母船的横向误差小,且波动范围更小;从图4(c)垂向误差对比图中可以看出,满意MPC下UUV与母船的误差变化比MPC下更为平滑,虽然稳态误差较前者偏大,但未发生超调,符合对接安全性的要求;从图4(d)的纵倾角误差可以看出,满意MPC比MPC波动更小,稳定时间更短,稳态误差小。从图4(e)的航向角误差可以看出,满意MPC比MPC的航向控制更为稳定,误差收敛速度更快,控制精度高。因此,综合图4的仿真结果图来看,在动基座UUV对接过程中,在约束条件下,满意MPC相比于MPC具有较好的稳定性与快速性。
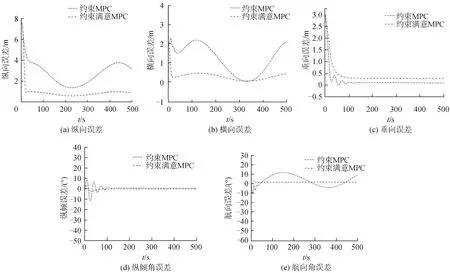
图4 UUV位置和姿态误差对比
从图5的UUV的速度对比图可以看出,满意MPC下UUV输出的速度、角速度更为平滑,这表明在存在海流干扰的情况下,满意MPC相比于MPC具有更强的抗干扰能力。除此之外,满意MPC使得UUV的(角)速度能够更快地稳定达到母船的(角)速度,这说明满意MPC在计算速度上要明显优于MPC。

图5 UUV速度和角速度对比
为了更真实的体现UUV与回收母船的对接轨迹,现将运动坐标系下UUV的中心点o′移动到对接柱下端o,即UUV的中心点o′纵向移动0.1 m,横向移动0 m,垂向移动0.3 m,UUV运动坐标系与大地坐标系之间的转换如图6所示。

图6 UUV运动坐标系转换
图7展示了UUV下端对接柱与回收母船的三维轨迹。从仿真结果来看,UUV下端的对接柱能够平滑地收敛到回收母船的运动轨迹,证明了所设计的约束满意MPC对接控制方法的有效性。
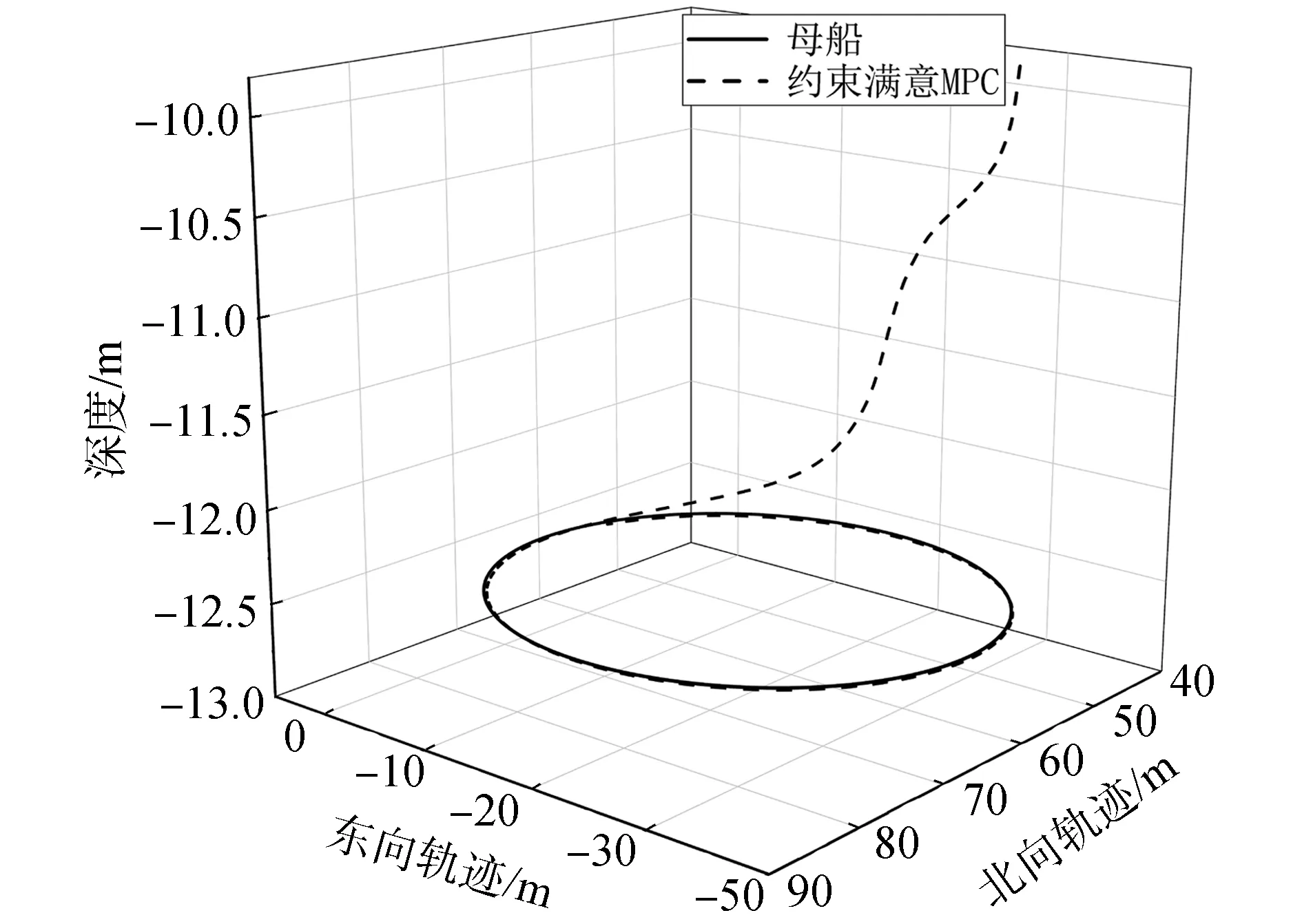
图7 对接柱与回收母船三维轨迹
5 结论
1)能够灵活处理UUV与运动母船对接过程中存在的各种复杂约束,与传统的MPC控制算法相比更加符合工程应用需求。
2)结合满意控制思想与MPC理论,设计了一种在复杂约束条件下的多目标多自由度满意MPC动基座UUV对接控制算法,减少了系统计算量,满足了多自由度同时最优。
3) 通过对MPC对接、约束满意MPC对接控制仿真结果分析,本文所设计的满意MPC在海流干扰下仍能实现UUV对运动回收母船的对接,达到了预期效果。
