一维无源对流扩散方程的近场动力学计算格式
2022-02-16王庆李家宝鞠磊薛彦卓贾定睿
王庆, 李家宝, 鞠磊, 薛彦卓, 贾定睿
(哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001)
对流和扩散是自然环境中常见的现象,包括河流、大气等污染中污染物的分布、流体流动、热运动、离子运动等[1]。扩散是微观上物质分子从高浓度区域向低浓度区域转移运动的现象,其扩散速率与物质的浓度梯度成正比;对流是宏观上物质传递的现象。对流扩散方程是流体力学中一个基本的运动微分方程,对于很多领域具有重要的应用价值,但是除了部分简单的情形,大多数问题无法得到精确解,只能利用数值方法进行模拟,因此对流扩散方程数值解法的研究具有重要意义。
从求解微分方程的方法上来说,目前主要的计算方法包括有限差分法[2-4](FDM)、有限元法[5-6](FEM)、有限体积法[7](FVM),基本思想是对求解区域进行网格划分,将微分方程离散化,把连续问题化为有限形式的线性代数方程组,求出原问题的近似解[8]。当对流占优时,传统的数值方法会产生数值震荡现象[9],为此需要合适的数值算法消除震荡。
近场动力学理论(peridynamics, PD)是近些年来快速发展的一种非局部理论[10-11],对于求解固体裂纹扩展的问题有非常高的适用性[12-14]。目前也已经成功应用到了包括热传导、电传导、水分浓度扩散等一系列常规非局部扩散问题上[15-19]。Bobaru等[18-19]构建了键基非稳态热传导方程,验证了方程的适用性,并对含裂纹板的热传导问题进行研究。Agwai等[20]推导出了态基近场动力学热传导方程,进而得到了简化的键基近场动力学热传导方程,提出了3种核函数形式及计算方法,给出了热传导方程在近场动力学格式下详细的数值实现步骤。Chen等[21]研究了不同响应函数下键基近场动力学热传导方程的计算参数收敛性问题。
除了扩散方程,采用近场动力学解决对流方程的研究也有了一定成果,Zhao等[22]采用中心差分格式和迎风格式的混合权重模型来计算对流扩散方程,但是原文中只是简单的采用扩散系数和对流速度绝对值的比值来判断对流和扩散的占优情况,并未考虑到网格大小的影响,其列举的对流占优例子实质为扩散占优,因此不能就此说明原文提出的计算格式适用于对流占优情况。
本文的主要目的是探究近场动力学理论求解一维无源项稳态对流扩散方程的可行性及数值上的准确性。在求解无源项对流方程的基础上,研究其中时间步长与空间步长的关系。同时引用无量纲数Pe考虑对流和扩散的主导地位,确定对流扩散方程的近场动力学求解格式,并与理论值进行比对分析。
1 近场动力学扩散模型
近场动力学研究扩散作用已经相当深入,以无源无汇的浓度扩散方程为例,采用键基近场动力学可以表示为:
(1)
式中:fh称为响应函数,代表物质点x′与x间的相互作用;Hx是点x的近场域范围;Vx′为点x′的体积;θ′和θ分别代表t时刻x′和x处的浓度。
响应函数通常有3种表示形式[20-21]:
f3=α3(θ′-θ)
(2)
式中α1、α2、α3为不同形式的微扩散系数。
本文选择第1种响应函数f1为例,对应的近场动力学扩散方程可表示为:
(3)
式中α为x′与x之间的微扩散系数。
为体现键长对扩散作用的影响,引入权函数ω。如式(4)所示,权函数ω通常有2种形式,常数形式表示键长不影响点与点间的相互作用;线性形式表示点与点间的相互作用随键长增加而减弱。如式(5)所示,将α表示成ω的函数。
(4)
(5)
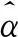
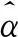
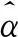
式中:α0是宏观的扩散系数;A表示离散后一维物质点的横截面积;h为二维板的厚度;δ表示物质点的近场域半径。
2 近场动力学对流模型
假设存在如图1所示的圆柱形界面[19,22],有离子沿圆柱体轴向发生对流运动,圆柱侧面无能量耗散。上、下界面面积为S,分别表示成S1、S2,上、下界面对应的浓度为θ1、θ2,界面相距为d,则单位时间离子总量变化可以写为[22]:
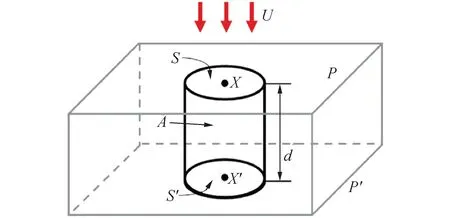
图1 离子沿圆柱轴向对流运动[19,22]
S(θ1-θ2)U·e(x,x′)
(6)
式中:U是对流速度矢量;e(x,x′)是沿圆柱体纵轴的单位矢量。
假设θa是圆柱体内的离子平均浓度,则单位时间内的离子总量变化可以写为:
(7)
在近场动力学中认为每个点只与其近场范围内的点具有相互作用,同样以近场动力学表示的对流方程,也认为每个点只与其近场范围内的点发生对流。依照近场动力学键基模型,认为作用域内的点与点之间存在相互作用,即为“键”,对流作用即是通过“键”产生的。
假定在空间域中的一点为x,在该点的作用域Hx中存在一点x′,则两点间的对流作用为:
(8)
式中:θ(x,t)和θ(x′,t)分别代表点x和x′在t时刻的离子浓度。
通过对x点整个近场域内的物质点进行积分,可以得到:
(9)
假设x点的平均浓度与键的平均浓度满足:
(10)
可以得到:
(11)
式中:u是点x和x′之间键的微速度矢量,满足u=ωU/VHx[22];VHx表示点x的近场域体积,同样以式(4)中的权函数ω表示键长对对流作用的影响:

(12)



3 数值实现
3.1 扩散方程离散
一维扩散方程离散形式为:
(13)
式中:m=δ/Δx,m称为邻域系数;Δx为离散后的粒子点间距。
xj是xi近场域内的一点,需要特别注意的是xj→xi的情况,无限趋近时2点可视为一点,虽然这种情况只存在于数学理论上,但该项表示的是点xi处浓度的空间变化率[18],不能忽略。离散的物质点具有体积,为了不使得物质点相互渗透,可以采用多种高阶精度格式来进行近似该项,通常情况下,采用二阶中心差分格式计算即可。由此,式(13)可以表示为:
(14)
3.2 对流方程离散
图3中U为宏观对流速度矢量。一维对流方程的离散形式与一维扩散方程的离散形式基本一致:

图2 一维扩散物质点分布(m=3)

图3 一维对流物质点分布(对流速度正向,m=3)
(15)
对流方程的离散同样需要讨论xj→xi的情况,不同于扩散方程的中心差分形式,对流计算需要考虑对流方向的影响。在对流的数值计算中,对流项处理不当会导致数值发散。流动方向会影响流动信息,理论上上游和下游会对彼此产生影响,但是两者的影响程度是不一样的,在同时包括从上到下的对流和自由扩散时,上游对下游的影响包括同方向的扩散和对流,而下游对上游的影响则取决于扩散和对流两者的比值,即Peclet数Pe,因为二者是反方向的。考虑到流动方向上的信息传输更为明显,xj→xi可以直接采用迎风格式进行近似:
以右为正方向,对流从左向右时:
(16)
对流从右向左时:

(17)
3.3 时间步长计算
时间积分统一采用向前显式积分,即:
(18)
因为涉及到对流和扩散2种模型,因此需要分别计算2种模型的收敛时间步长。
扩散的收敛时间步长计算公式[23]:
(19)
式中ξij表示xi和xj的位置矢量,显然‖ξij‖最小为Δx。将一维扩散系数的常数权函数形式代入式(19),放缩后可取等号得到:
(20)
同理可以得到:
(21)
对扩散方程的离散格式和时间步长进行验证,计算模型为一块有限尺寸的厚板[23],在其表面施加一个随时间线性增长的温度边界条件。具体模拟参数如表1所示。

表1 温度扩散计算参数
板的初始温度为0 ℃,边界条件为:

(22)
温度T的理论解:
(23)
式中:n可以取一个较大的数值,在本文中,取n=100。
从图4可以看出,理论值和PD计算值的对比结果吻合较好。在文献[23]中采用的时间步长为10-6s,由式(20)计算出的范围为:Δt1<3.5×10-7s,为了方便计算,本文取为10-7s,可以看出由于经过放缩过程,由式(20)得到的时间步长取值范围比式(19)计算出的要小,但是其结果也是必定满足收敛条件的。

图4 一维热扩散PD计算值与理论值对比
下面以正向对流运动为例对一维对流方程的收敛时间步长进行推导。此处及后文的u和U均为标量,由扩散过程的数值稳定性推导可以类比得到一维对流方程收敛的时间步长估算公式:
(24)
(25)

为了明确PD计算值与理论值的对比结果,将二者的相对误差定义为:
(26)
式中N为模型内部的物质点数目。
4 对流模型验证
本节以三角函数为研究对象,验证近场动力学格式的对流方程在数值应用上的准确性。
一维无源对流方程可以写为:
(27)
式中U为对流速度,上述方程的理论解可以写为三角函数的形式:
θ(x,t)=0.5sin(2π(x-Ut))
(28)

图5 近场动力学对流离散模型
初始条件:θ(x,0)=0.5sin(2πx);
左右虚拟边界条件:θ(x,t)=0.5sin(2π(x-Ut));
变量取值:x∈[0,2]m,t∈[0,0.5]s,U=1 m/s。
该三角函数周期为1 s,选定计算时长为半个周期,即为0.5 s。
从图6可以看出,PD计算出的函数值与理论值较为接近,由式(26)得到的计算误差为2.60%,在可以接受的范围内,证实了采用近场动力学求解对流方程的可行性。
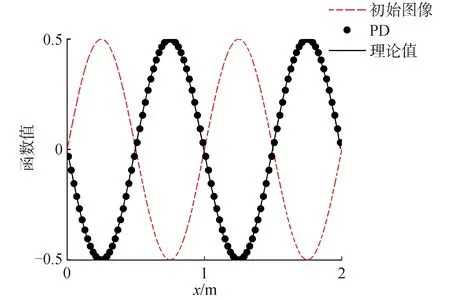
图6 函数初始图像及t=0.5 s时的函数图像(Δx=L/100, m=3)
近场域范围系数通常取m=3[12],但是由于引入了安全系数,因此为了得到安全系数取值对计算结果误差的影响,以Δx=L/100,L/200,L/500为例,分别取m为3、4、5,综合考虑安全系数、离散格式和近场域范围系数等因素对计算结果的影响,得到以下结果。
从表2~4中能够看出:1)随着离散物质点数的增加,同一邻域系数m及安全系数对应的计算误差逐渐减小;2)相同邻域系数m及离散格式下对应的误差呈现出先减小后增大的趋势,当邻域系数m与安全系数的倒数满足1/ζ=2m时,可以得到最小的计算误差;3)整体趋势上,随着邻域系数m的增大,相同条件下的计算误差增大,因此在计算时可以直接取m=3,当物质点间隔足够小时,如Δx=L/500,在误差可接受的范围内,为了方便计算,m也可以取其他值。
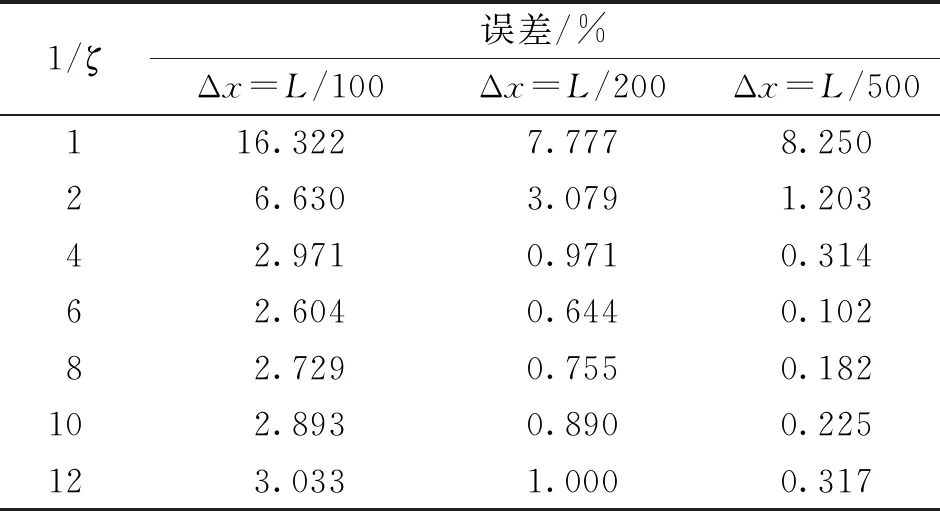
表2 m=3时不同的安全系数对应的计算误差
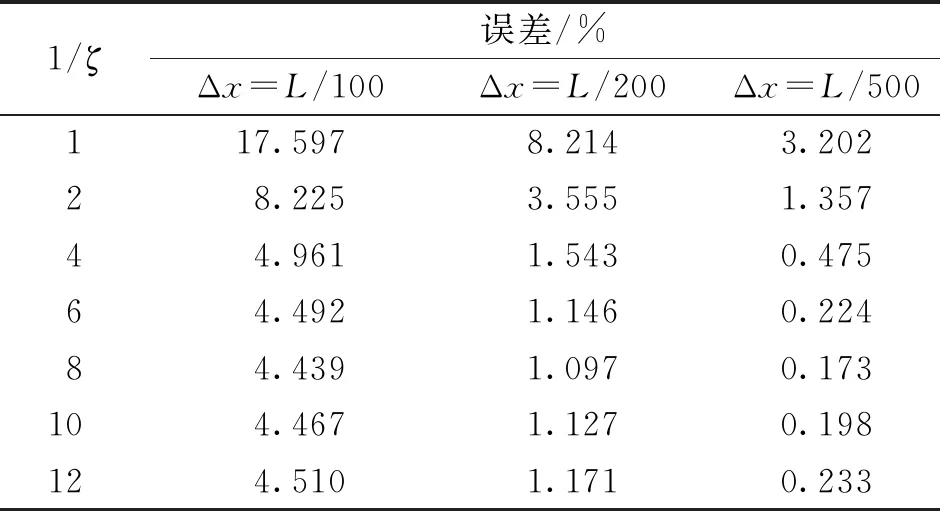
表3 m=4时不同的安全系数对应的计算误差

表4 m=5时不同的安全系数对应的计算误差
5 对流扩散模型验证
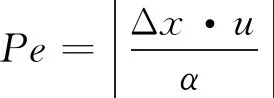
将采用近场动力学理论描述的扩散和对流方程合并,可以得到无源项的一维对流扩散方程:
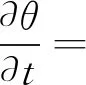
(29)
式中θ′和θ分别代表t时刻x′和x处的浓度。将一维对流方程的离散式(14)和一维扩散方程的离散式(16)或式(17)结合起来即可得到式(29)的离散形式。
本节仍然以三角函数为例对基于近场动力学的一维对流扩散方程进行验证:
(30)
其理论解为:
θ(x,t)=e-4α0π2t0.5sin(2π(x-Ut))
(31)
从理论解的形式可以看出:在一个周期的时间内,只发生扩散时函数幅值会减小;只发生对流时函数的峰值位置会向对流的正方向移动;若二者同时发生,当其中一者占优时,另一者的现象会较弱;而二者均不占优时,双方的现象会较明显。
5.1 扩散占主导地位
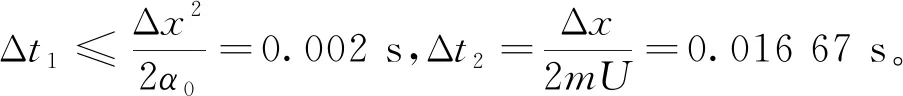
从图7可以看出,随时间的变化,函数的波峰、波谷的位置没有发生明显的改变,而函数幅值有了明显下降,这说明计算中主要发生了扩散现象,导致幅值迅速减小,这个现象与计算时的假设一致。而且从理论值与计算值的比对可以看出计算误差比较小,计算结束时的相对误差为2.43%。

图7 扩散占优时不同时刻的函数值对比
5.2 对流占主导地位
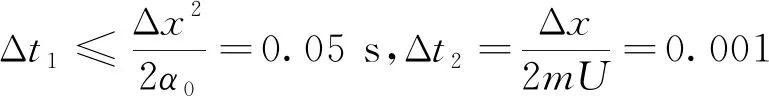
从图8可以看出随时间变化,函数的幅值未发生明显的变化,但是波峰、波谷的位置产生了显著的位移,也即是对流现象明显,与假设的情况一致。计算结束时,相对误差为1.653%。
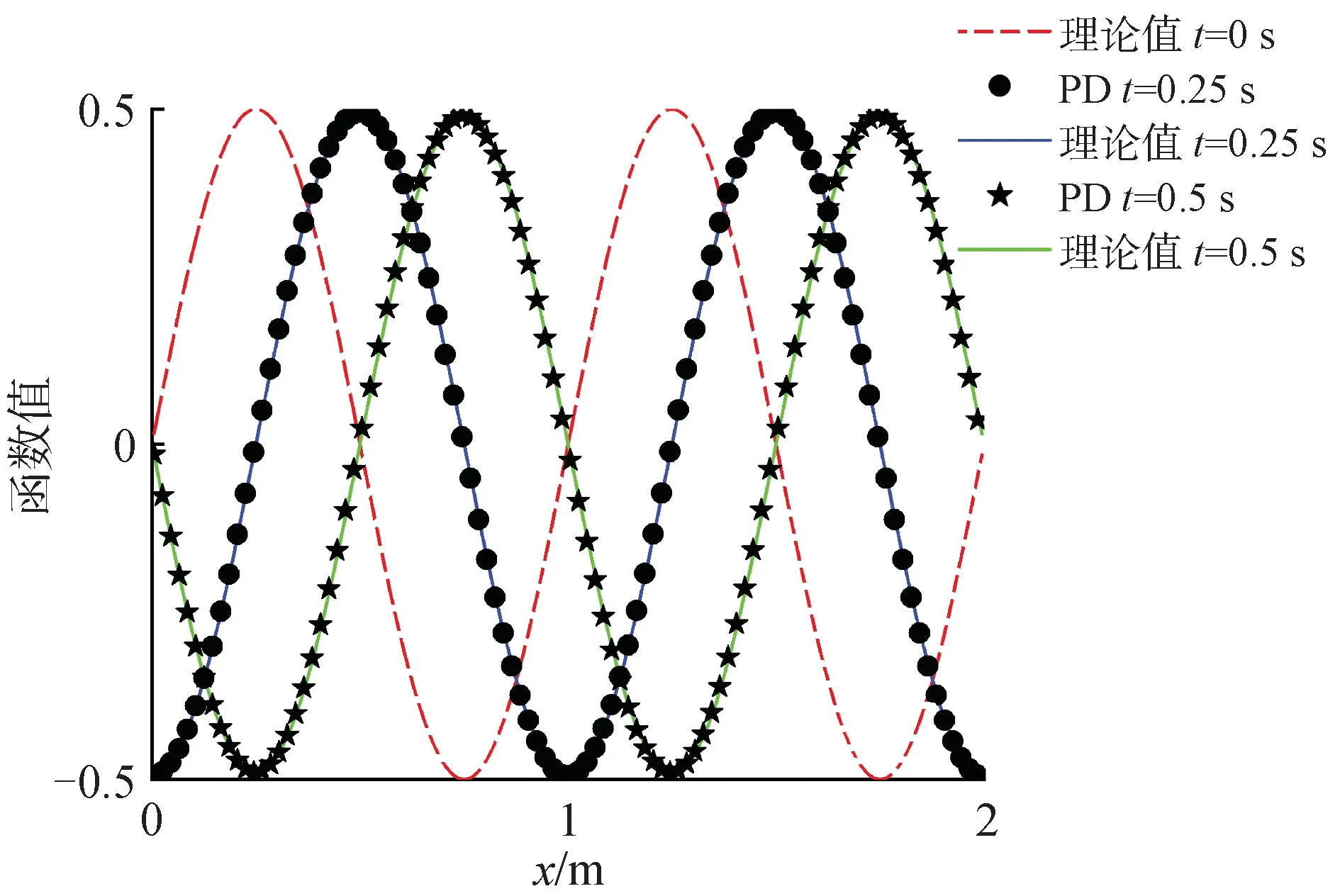
图8 对流占优时不同时刻的函数值对比
5.3 对流和扩散均不占优

在Pe=1时,从图9看出,随时间的变化,函数的波峰、波谷均产生了明显的正向位移,同时幅值减小。这2种现象都可以从图上明显观察出来,也就证明了对流和扩散实际上均不占优,计算结束时的相对误差为1.478%。
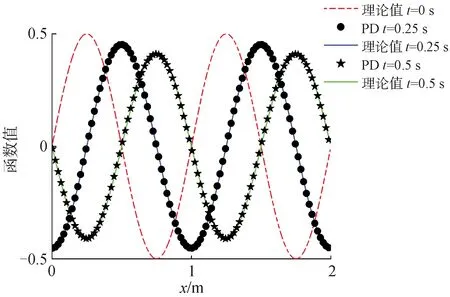
图9 对流扩散均不占优时不同时刻的函数值对比
通过以上算例,证实了无量纲数Pe可以用于判断对流和扩散现象是否占优,同时也验证了本文构建的近场动力学对流扩散模型的准确性。
6 结论
1)本文成功构建了一维无源近场动力学对流扩散模型,并在数值上验证了该模型的有效性和准确性;
2)当采用一阶迎风格式计算一维无源近场动力学对流模型时,时间步长的安全系数ζ与近场范围系数m满足1/ζ=2m时,模型的相对误差可以取到最小值;
3)无量纲数Pe可以用于判断对流和扩散的占优性,推导的对流和扩散的收敛时间步长公式可用于确定同时满足二者要求的时间步长,最终的数值结果满足预期结果;
文中引入的无量纲数Pe和物质点间距有关,因此,离散格式对于Pe的影响以及单元相关性还需要进行进一步的研究。
