分块迭代导向最小方差算法及其在线谱目标检测中的应用

郭浩泉， 朱代柱,2

(1.上海船舶电子设备研究所， 上海 201108； 2.水声对抗技术重点实验室， 上海 201108)

高方位分辨力的波束形成在目标检测、参数估计与识别中具有重要的意义，在多目标和强弱目标同时存在的情况下，有效抑制多目标相干干扰是后续信号处理的基础。导向最小方差(steered minimum variance, STMV)波束形成算法以其高方位分辨力、无旁瓣以及良好稳健性等优越性能而受到广泛关注，其中最主要的运算量取决于协方差矩阵的求逆过程，对阵元数为M的基阵进行经典STMV分析，每个导向方位的每个频率点都需要进行O(M3)次乘法运算[1-2]，这对大规模基阵的宽带信号处理是难以承受的，必须寻求更低复杂度的简化算法。

为了降低STMV算法中矩阵求逆过程的复杂度，许多学者做了大量研究，基本可以归纳为降维处理、递归迭代、矩阵分解和矩阵分块4大类方向：1)在降维处理方面，文献[3-7]主要利用盲分离的自适应波束形成、对导向矢量进行处理以降低干扰的自适应波束形成、结合稳健Capon波束形成器和Krylov子空间、基于阵形在线估计聚焦和Krylov子空间等降维技术。2)在递归迭代方面，文献[8-9]主要利用基于统计优化准则的迭代MVDR算法、基于矩阵求逆引理的递归MVDR算法进行迭代运算减少计算量，文献[10]提出了基于一阶递归滤波器和矩阵求逆引理的迭代STMV算法，将计算量降低至经典STMV算法的2/M。3)在矩阵分解方面，文献[11] 主要利用基于QR分解的自适应波束形成算法将求解权向量的问题转化为求解三角线性方程的问题，避免了自相关矩阵的估计和求逆运算；文献[12-14]提出了子阵STMV波束形成算法，大幅度降低了运算量。4)在矩阵分块方面，文献[15-17]主要利用协方差矩阵为正定Hermite阵的对称性并结合Strassen矩阵求逆的高效性降低协方差矩阵求逆的复杂度。

这些研究将全阵平均分为多个子阵的矩阵分解方法计算量最小，但由于削弱了子阵之间的信号相关性，在本质上是一种近似算法，所以与全阵STMV算法相比性能略有损失；并且，如何分配子阵数目和子阵阵元数成为一个绕不开的问题，缺乏寻求最优解的理论依据。其他降维处理、递归迭代和矩阵分块研究方面，计算量最小的是文献[10]在保持STMV性能的同时将计算量降低至经典STMV算法的2/M。

本文针对经典STMV的大运算量问题，提出了一种低复杂度的BISTMV算法，通过对矩阵求逆公式的层层分解与分块迭代，可以大幅度降低协方差矩阵求逆的复杂度，更加有利于工程应用。

1 导向最小方差波束形成

1.1 STMV的基本原理

基于导向协方差矩阵的导向最小方差波束形成算法的基本原理是通过波束旋转，使指定方向的响应为1，而阵列输出功率最小。

假设各阵元时域输出为x(t)=[x1(t)…xM(t)]T，相应的频域输出为X(fk)，各阵元的权向量为W=[w1w2…wM]T，则导向矩阵为：

(1)

式中：M为阵元数；θ为方位角；d为阵元间距；c为声速。

阵列的输出为：

(2)

式中：h为频率点上限；l为频率点下限。

阵列输出的平均功率为：

P(θ)=E[y(t,θ)y(t,θ)H]

(3)

STMV波束形成器的最佳权向量w是使指定方向的响应为1，而阵列输出功率最小，故：

(4)

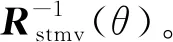
1.2 迭代STMV算法原理

STMV波束形成时，对N次快拍的频域输出Xn(fk)进行求和，得到平均频域输出为：

(5)

则导向协方差矩阵Rstmv(θ)可表示为：

(6)

(7)

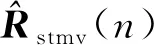
(8)

式中：α为一阶递归滤波器的系数；β=1-α。

由矩阵求逆引理：

(9)

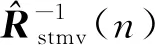
(10)

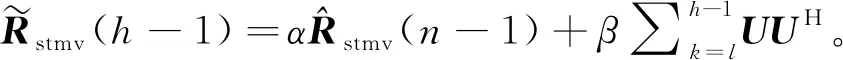
(11)

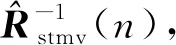
1.3 分块迭代STMV算法原理

1.3.1 分块矩阵求逆算法

关于2阶分块矩阵的求逆公式，文献[18]已详细阐述。

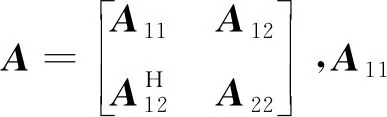
(12)

(13)

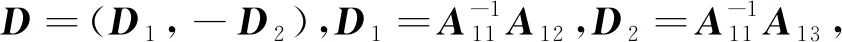
把式(13)命名为“组合求逆公式”。

证明考虑到：

则

(14)

式中E-1可由式(12)求得。

(15)

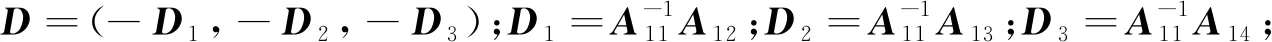
1.3.2 算法原理

假设U被等分成K段，记为Ui，i=1,2，…,K，每段的长度为k=M/K。则导向协方差矩阵Rstmv(θ)被等分成K×K块，每块矩阵的阶数为k。考虑到Rstmv(θ)为埃尔米特矩阵，则式(7)可表示为：

(16)

(17)

2) 构造矩阵

(18)

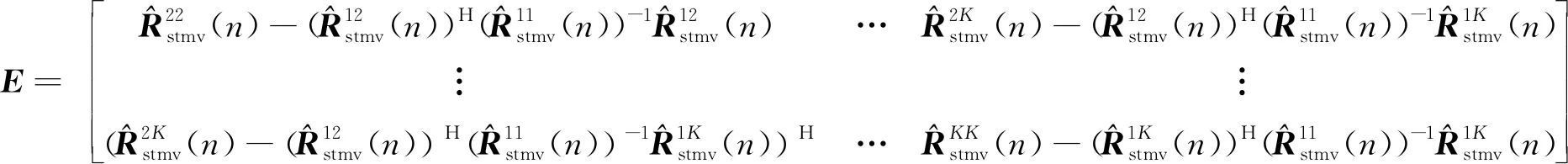
(19)

3) 应用分块矩阵求逆公式递推求解E-1；

2 计算量分析

2.1 经典STMV算法计算量

假设阵元数为M，信号带宽为B，利用N次快拍的频域输出估计互谱密度矩阵，注意到乘法运算的计算时间为加法运算的数十倍(约40倍)，因此本文仅考虑乘法运算的计算量。其计算量主要集中在2部分：

1)估计互谱密度矩阵时，需在每个频点处需进行NM2次乘法运算，总共需进行NM2B次乘法运算；

2) 估计空间谱估计时，需在每个波束进行如下计算：

①估计导向协方差矩阵，在每个频点处需进行2M2次乘法运算，总共需进行2M2B次乘法运算；

②对导向协方差矩阵求逆需进行M3次乘法运算，然后利用式(4)进行空间谱估计，需进行M2+M次乘法运算。

综上所述，假设对L个波束进行空间谱估计，所需的计算量为：

NM2B+[M3(2B+1)+M2+M]L

(20)

2.2 迭代STMV算法计算量

假设m阶矩阵求逆的计算量为C(m)，则根据式(12)、(14)、(15)，2×2、3×3、4×4分块矩阵求逆的计算量依次为：

x2=2C(m)+4m3

(21)

x3=x2+C(m)+11m3

(22)

x4=x3+C(m)+21m3

(23)

综上所述，考虑n×n分块矩阵求逆的计算量的通项公式。n×n分块矩阵求逆的计算量为：

(24)

结合式(21)～(23)，可得通项公式为：

3(n-1))m3

(25)

假设阵元数为M，信号带宽为B。其计算量主要集中在2部分：

综上所述，假设对L个波束进行空间谱估计，所需的计算量为：

[M2(4B+1)+M(B+1)]L

(26)

2.3 分块迭代STMV算法计算量

假设阵元数为M，信号带宽为B，U被等分成K段，记为Ui，i=1,2，…,K。每段的长度为k=M/K。其计算量主要集中在5部分：

4) 利用分块矩阵求逆公式求解E-1，需进行(K-1)C(k)+((K-2)3+4(K-2)2+3(K-2))k3/2次乘法运算；

综上所述，假设对L个波束进行空间谱估计，所需的计算量为：

(M2B+(3k2+k)B+(K(K+1)/2-1)k2B+

(K-1)C(k))L+((K-2)3+4(K-2)2+

3(K-2))k3L/2+((K-1)2k3+(K-1)k3+

M2+M)L

(27)

式中：C(k)为k阶矩阵求逆的计算量，取C(k)=k3。同时考虑到k=M/K，式(27)可化简为：

(28)

(29)

假设信号带宽B=5 kHz，在0°～180°方位内每隔2°形成一个预成波束，即对L=91个波束进行空间谱估计，快拍数N=4，K=16，STMV算法与分块迭代STMV算法计算量的比值随阵元数M的变化如图 1 所示。

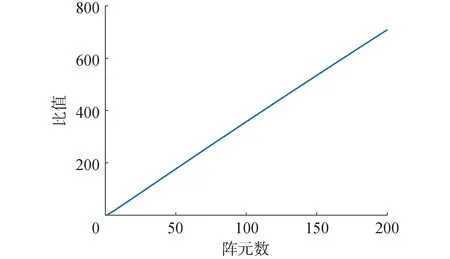
图1 2种算法计算量比值

文献[10]提出的迭代算法的计算量大致是STMV算法计算量的2/M。为便于分析，同时考虑到L≫N、B≫M，式(20)和式(29)分别可近似化简为：

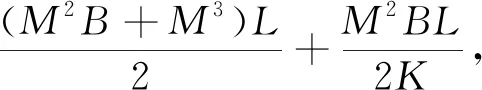
(30)

当K足够大时，本文提出算法的计算量大致是原STMV算法计算量的1/4M，约为文献[10]迭代STMV算法计算量(2/M)的1/8。当M≫5时，计算量显著降低。

3 仿真分析

仿真条件如下：设48元均匀线阵接收，阵元间距d为信号上限频率对应的半波长，每快拍处理时间为3 s，采样频率为fs，处理带宽为0.05～0.25fs，声速为1 500 m/s。两目标辐射噪声信号及背景噪声均为相互独立的高斯白噪声，目标1的方位为30°保持不变，阵元输入端信噪比为6 dB；目标2的初始方位为50°，阵元输入端信噪比为0 dB，在0.1fs处叠加一根线谱，该线谱相对于周围连续谱的信噪比为15 dB，对总能量的贡献可忽略不计，目标2每快拍的目标方位增加0.4°。取α=0.5，由STMV算法和分块迭代BISTMV算法(K=6)估计的130 s空间谱历程图看不出明显差异，截取不同时刻的空间谱如图2所示，图3为图2(b)的局部放大图。

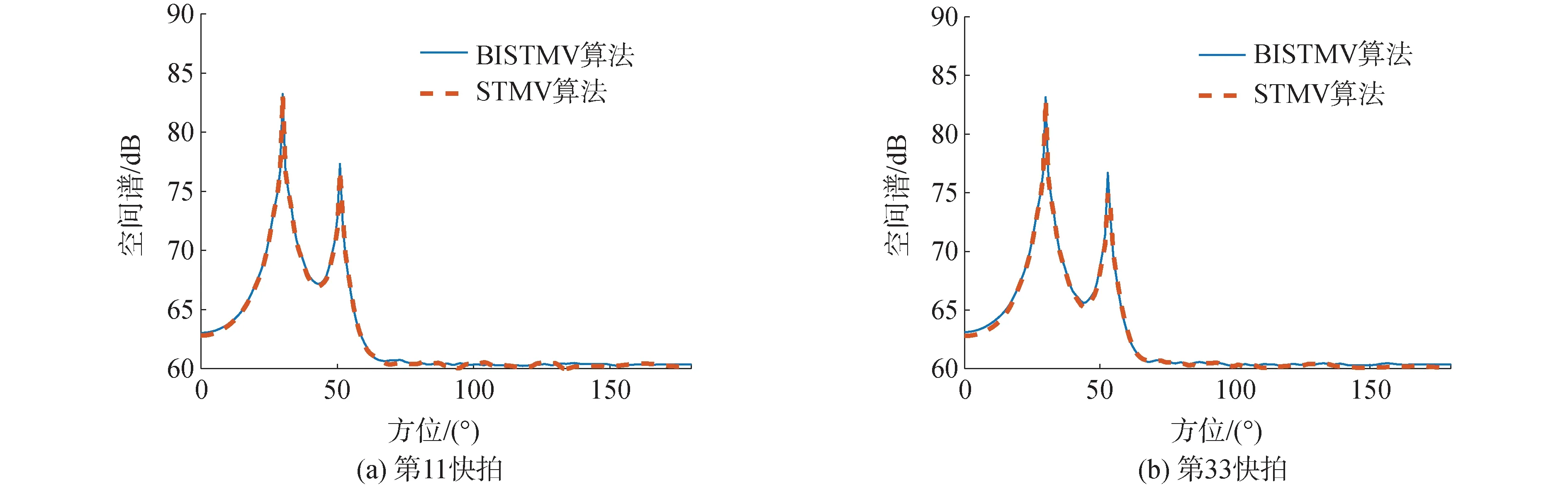
图2 不同时刻2种算法的空间谱

图3 线谱目标局部放大图

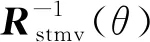
4 海试数据分析

为验证算法的稳健性，对海上试验数据进行处理，试验态势如图4所示。以拖船的航向为0°且直线航行，其后拖着一条均匀线列阵。目标1距离拖船较近，其辐射噪声较强，目标4的初始方位为75°且朝着拖船方向航行。试验时，航运繁忙且目标3、4相对于目标1、2距离拖船较远，其辐射噪声较弱。

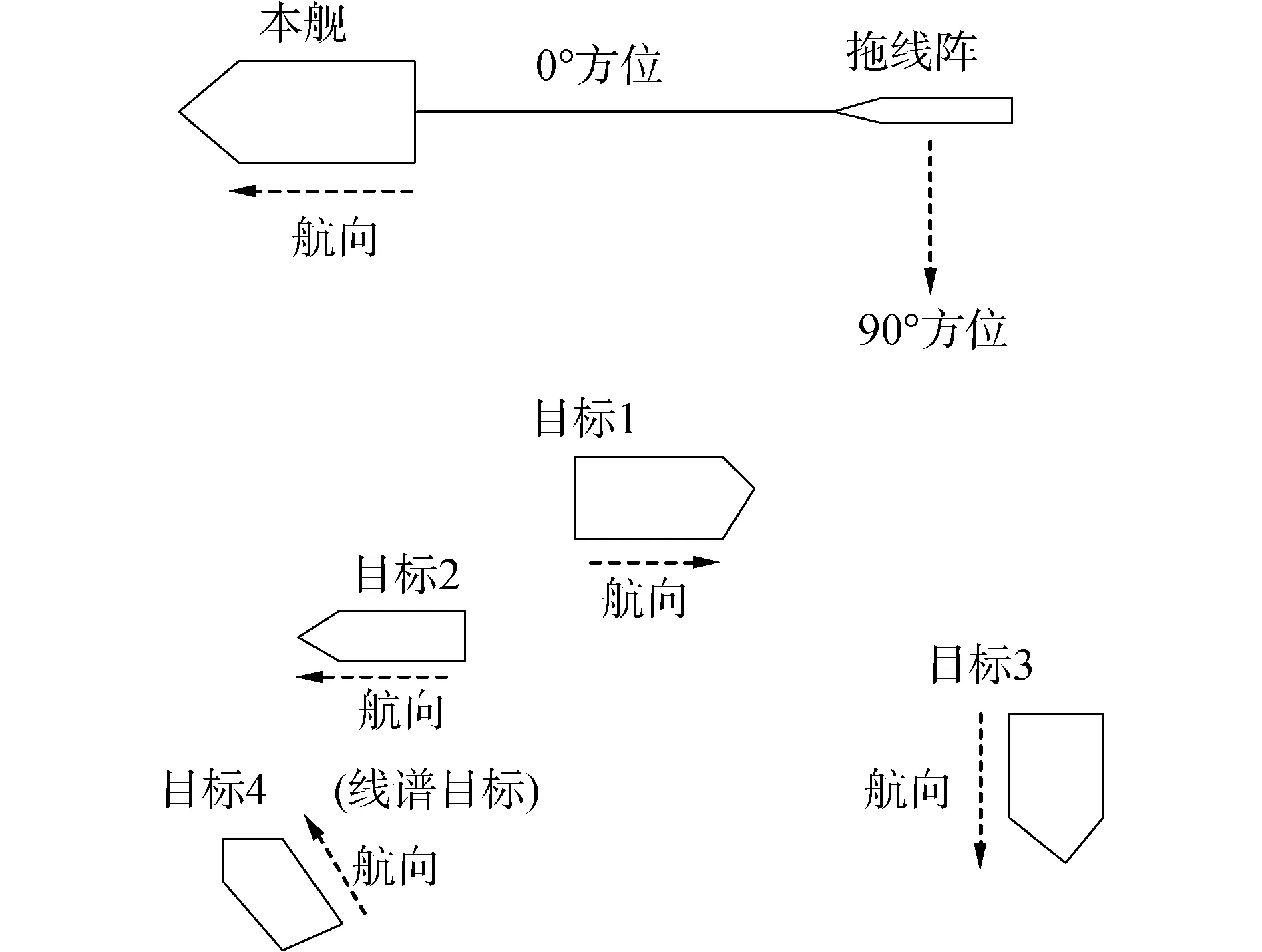
图4 试验态势

对接收信号进行预成波束形成，处理带宽为0.025～0.1fs，由STMV算法和BISTMV算法(K=6)估计的空间谱历程图也看不出明显差异，截取第88 s和141 s时刻的空间谱，如图5所示，当存在强目标时(目标1、3)，仍可实现对弱目标(目标2、4)的有效检测。

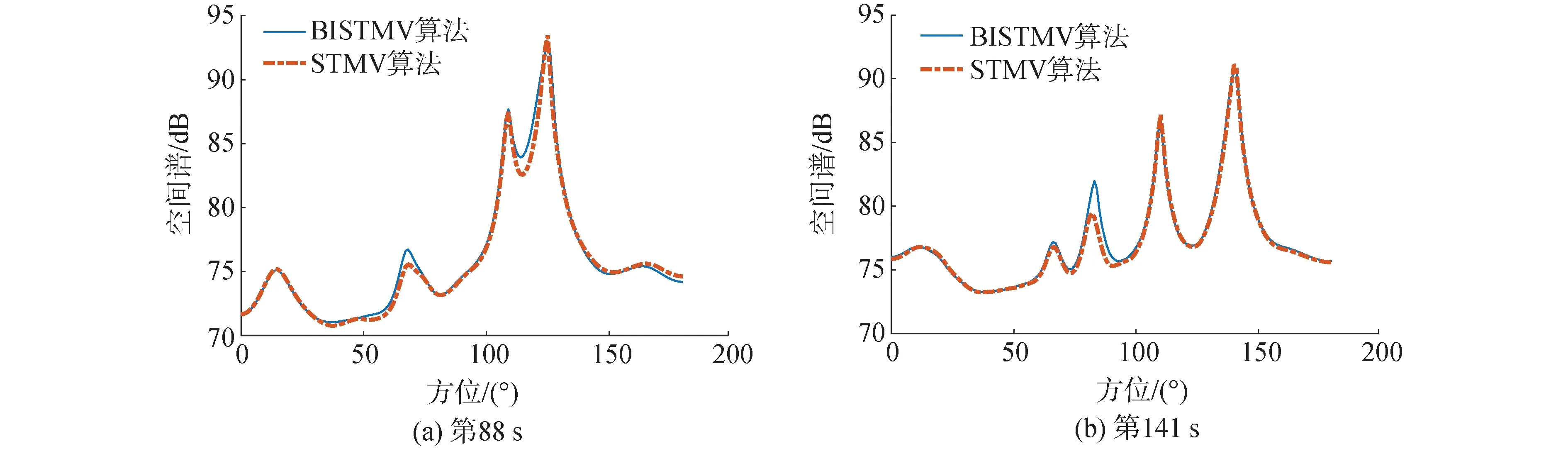
图5 88 s和141 s 2种算法的空间谱

由图5(a)和5(b)可以看出，BISTMV算法在同时存在多个强弱目标的情况下，对每个强弱目标的检测效果都与STMV算法比较贴合，对其中的线谱目标还有1～4 dB(平均2.2 dB)的检测增益,如图6(a)和6(b)所示。究其原因，是由于BISTMV算法在式(8)对协方差矩阵进行求逆的过程中引入了一阶递归滤波器。一阶递归滤波器将前后快拍之间的信息进行了关联，由于目标辐射噪声信号是平稳相关的，而背景噪声是弱相关的，因此，这种关联在大多数情况下对目标检测是有利的：当处理宽带信号时几乎没有差异，但当处理窄带信号时效果会有改善，尤其是当目标辐射噪声信号中包含有窄带线谱信息时(如图5(a)和5(b)中75°左右的目标4)；只有当目标方位快速变化时，这种关联才会略微展宽该目标所在波束的宽度(如图5(a)中127°左右的目标1)，造成轻微负面影响。但总体而言，BISTMV算法在继承STMV算法的优良特性的同时大幅减小了计算量，对窄带线谱信息丰富的目标检测还可以获得一定程度的增益提升。

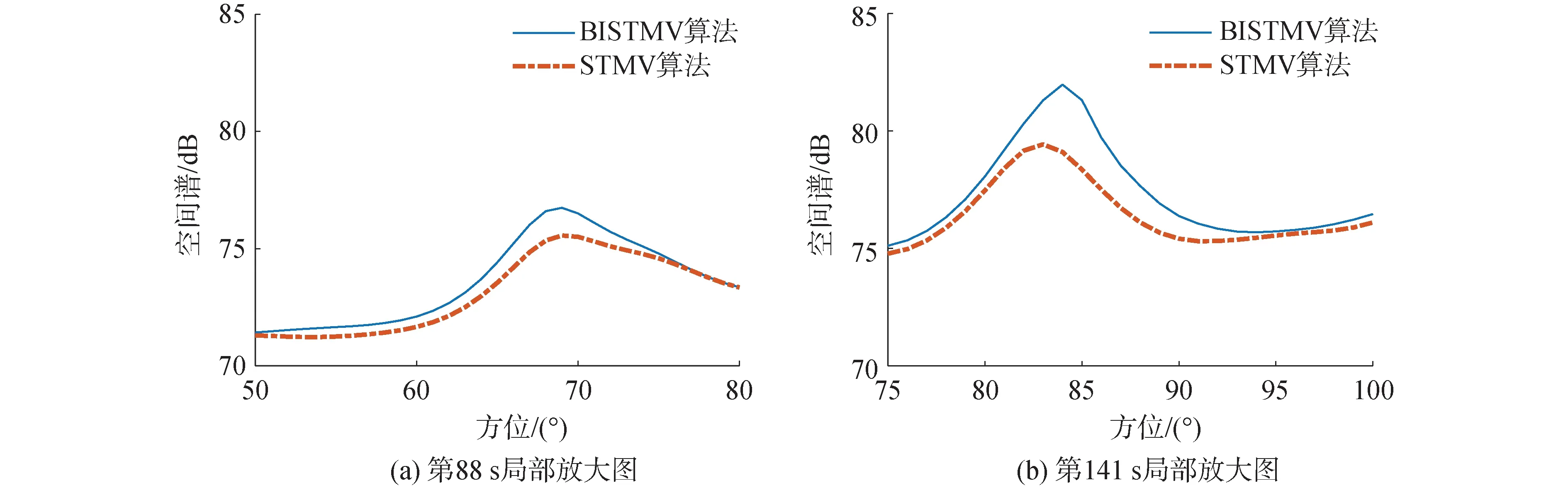
图6 线谱目标局部放大图

5 结论

1)本文提出了基于一阶递归滤波器、矩阵求逆引理和矩阵分块求逆的BISTMV算法，进行了计算量分析，大致是经典STMV算法计算量的1/4M，是迭代STMV算法计算量的1/8，显著减小了计算量，提高了其工程可实现性。

2)仿真和海试数据处理结果表明，该算法保持了STMV算法高方位分辨力和对微弱目标检测的优势。

3)该算法对窄带线谱信息丰富的目标检测可以获得平均2 dB左右的增益提升，对工程应用，特别是线谱目标的检测具有重要的意义。