基于自适应动态逆的着舰控制器设计

王双双, 李春涛,*, 王 震, 苏子康, 戴 飞

(1. 南京航空航天大学自动化学院, 江苏 南京 211106; 2. 中国人民解放军94804部队, 上海 200434)

0 引 言

随着无人机的应用发展,着舰控制技术逐渐成为无人机海上作战研究的重要方向之一,不同于无人机常规着陆,舰载无人机受到舰尾流、甲板运动等干扰影响,需要在复杂环境下沿着相对下滑轨迹飞行,并且着舰区域十分狭小,对落点精度要求高[1-4]。此外,无人机着舰时往往处于速度不稳定区域,飞行动压低,对风扰敏感。因此舰载机着舰控制问题实质上是低动压下的稳定飞行控制与下滑轨迹的高精度跟踪问题[5-8]。

早期着舰控制技术主要采用经典的控制方法,但是在复杂的着舰环境下，常规的控制方法难以使舰载机达到良好的着舰性能。因此国内外学者提出了许多基于现代控制理论的改善方法[9-15],文献[16]设计了一种鲁棒自适应着舰姿态控制律,并利用非线性扩张观测器估计舰尾流扰动,有效提高了控制器存在对象不确定以及外界干扰时的适应能力,但是该研究是基于小扰动线性化模型进行的,没有考虑对象的非线性特征。文献[17]建立了无人机非线性数学模型,采用非线性动态逆方法抵消对象中的非线性,但是动态逆方法对模型的精确度要求高,无法克服系统中存在不确定性。文献[18]提出一种指令滤波反步滑模着舰控制方法,处理了反步控制时的计算膨胀问题，并且利用高阶滑模思想降低了滑模控制引起的抖动,有效抑制了着舰过程中的风扰影响。文献[19]在着舰轨迹跟踪稳态性能的基础上研究了瞬态性能,提出了受限指令预设性能控制方法,理论推导与仿真结果表明，该方法在复杂环境下有较好的瞬态与稳态性能。文献[20]基于自适应反推方法设计了一种输出反馈控制律,实现了推力饱和情况下飞行轨迹角的精确跟踪。

本文在舰载无人机非线性模型的基础上,设计了自适应动态逆控制器,考虑了无人机动力受限的实际问题,在存在环境不确定和外部干扰的情况下,保证姿态与速度闭环系统的动态性能与稳态性能,实现无人机对复杂环境的鲁棒性和着舰轨迹的精确跟踪。

1 问题描述

舰载无人机飞行控制问题实质是在复杂环境下,对下滑轨迹进行精确跟踪的问题,其难点主要有以下3点[21-28]。

(1) 外界扰动复杂。无人机在着舰时受到舰尾流、常值风等干扰,并且大迎角、低动压的飞行状态使得无人机对风扰变得更为敏感,因此控制器需要具有较强的抑制风扰能力。

(2) 非线性耦合以及参数不确定性。无人机在飞行状态变化大时，会呈现强非线性耦合特性,控制器需要具有克服匹配不确定性和非线性耦合的能力。

(3) 速度自稳定能力弱。如图1所示。样例无人机着舰时速度为54 m/s,即临界速度的左边,处于速度不稳定区域,若不加控制会导致速度持续不稳定,进而导致无人机无法准确地跟踪着舰轨迹。因此需要研究动力补偿系统,通过调节推力大小补偿速度偏差。

针对无人机低动压着舰飞行问题,建立无人机非线性模型如下:

(1)

式中:V、α、θ、q、γ、H分别是空速、迎角、俯仰角、俯仰角速率、航迹倾斜角和高度;Iyy为绕俯仰轴的转动惯量;m、g分别为无人机的质量和重力加速度;ρ是空气密度;Sw是机翼参考面积;cA是机翼的平均气动弦长;δT是油门开合度,其范围是[0,1]；Tmax表示发动机的最大推力;δe是升降舵舵偏角;CL0、CLα、CLδe、CD0、CDα2、Cm0、Cmα、Cmq、Cmδe是空气动力系数。

2 基于自适应动态逆的着舰控制系统

将式(1)中q和V的动力学方程转化成如下仿射非线性系统的形式:

(2)

式中:x=[q,V]T表示系统的状态变量;u=[δe,δT]T表示控制变量;f(x)∈R2×1表示非线性动态函数;g(x)∈R2×2是非线性控制分布函数,其形式如下:

(3)

则对于可逆的g(x),通过对式(3)求逆系统就能够在控制输入u处抵消非线性以及多变量耦合,并使状态q,V以期望的动态运动。

2.1 着舰姿态控制器设计

结合式将俯仰角速率动力学方程改写为

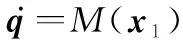
(4)

式中:x1=[q,α,Q,V]T,M(x1),N(x1), ϑ,ζ形式为

(5)

dw表示由风扰引起的系统未知建模误差,无风扰时dw=0;M(x1)和N(x1)包含常量Sw,cA以及可测信号量Q、q、α、V;ϑ和ζ包含气动系数和转动惯量。

dw=0时,对式(4)进行代数求逆可得控制输入为

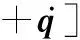
(6)

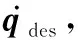
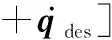
(7)

设俯仰角速率指令为qc,定义状态跟踪误差为

ed=q-qc

(8)

将式(8)对时间求导,则误差动态系统为

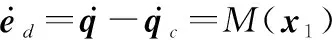
(9)

进一步得到控制输入为

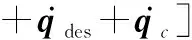
(10)

(11)

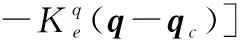
(12)

进一步地,结合式(9)和式(12)可得

(13)

当系统存在参数不确定性,为保证跟踪性能,对ϑ、ζ和dw进行估计,得到控制律为

(14)

(15)

(16)

(17)

由此可得参考模型跟踪误差为eq=q-qref,将式(16)减去式(17)得到

(18)

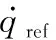
定理 1对于系统(4),采用控制器式(14)和自适应律式(15),可以使系统满足:

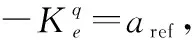
(19)

(20)

根据矩阵迹恒等式得

(21)

联立式(20)和式(21):

(22)

根据式(15),式(22)可以写为

(23)

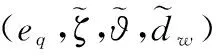
(24)

证毕

(25)

2.2 基于速度控制的动力补偿系统设计

发动机通道进场动力补偿系统可以自动调节油门大小以维持无人机在着舰过程中的速度稳定,削弱升力波动对速度的影响。由于俯仰角姿态回路是轨迹跟踪的内回路,动态响应快,其带宽高于速度回路,因此通过双通道分别控制姿态和速度能够实现时间上的解耦。

根据式(22)可知空速V的动力学方程为

(26)

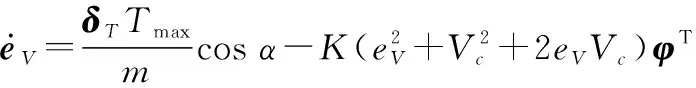
(27)

2.2.1 动力不受限的速度控制

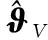
(28)

(29)

定理 2假设发动机推力不受限,对于系统(26),采用控制器式(28)以及自适应律式(29)使得系统满足:

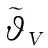
(2) 速度跟踪误差eV收敛至0。

证明定义Lyapunov函数为

(30)

式(30)沿误差动态的时间导数为

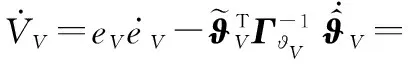
(31)

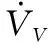
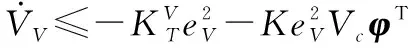
(32)

证毕

2.2.2 动力受限的速度控制

当推力达到上限或下限时,自适应律将会过度补偿阻力系数直至速度达到指令值,需进一步修正自适应律,保证推力饱和时自适应估计参数的有界性和动力补偿系统的稳定性。修正后的混合自适应律为

(33)

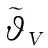
设最小推力为0,油门开合度范围为δT∈[0,1],因此,以下不等式成立:

(34)

(35)

证明 1推力达到上限时,δT=1

如果油门开合度不小于1,可以得到:

(36)

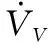
(37)

(38)

根据式(36),进一步可得

(39)

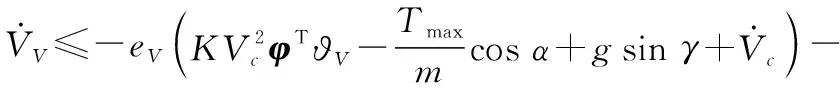
(40)

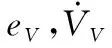
证毕

证明 2推力达到下限时,δT=0

由式(28)和式(34)可得

(41)

(42)

结合式(42)可知Lyapunov函数导数的极性取决于eV的符号,当eV≤0时,代入式(29)可得

(43)

根据不等式(41)得

(44)

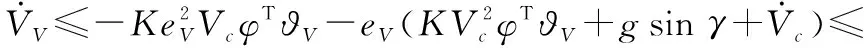
(45)

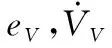
证毕

3 仿真验证

舰载无人机在着舰过程中除了受到常值风扰等常规大气扰动外,在将受到舰尾气流影响。而舰尾流是影响着舰安全的重要因素之一[29],根据MIL-F-8785C军用规范,其主要由尾流的周期分量、随机分量、稳态分量以及自由大气紊流分量组成。参考文献[30],舰船航行速度为10 m/s,甲板风速为12 m/s时的舰尾流曲线如图2所示

可以看出水平分量的最大幅值约为2.3 m/s,垂直分量的最大幅值约为1.7 m/s。

3.1 仿真条件

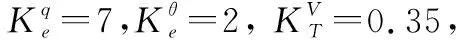
为验证控制器复杂环境下的跟踪性能,在距离舰船1 460 m处加入常值风扰(水平风、侧风和垂直风),在距离舰船800 m处加入舰尾流。

当无人机存在参数不确定性时,设置参数气动系数拉偏为:K_Cm0=1.3,K_Cmα=1.3,K_CDα2=1.3K_CD0=1.3,其为无人机真实参数与理想参数的比值,则真实参数表达式为

(46)

无人机及舰船初始条件为:舰船的前向距离设为0 m,高度为0 m,航行速度为10 m/s。无人机初始高度为116 m,前向距离为3 000 m,迎角为5°,飞行速度为54 m/s,俯仰角为5°,理想相对下滑轨迹角为-3°。

3.2 控制效果

3.2.1 常值风扰环境

图3～图7分别为水平风5 m/s和垂直风±1 m/s影响下的无人机俯仰角、下滑角、飞行速度、油门开合度以及升降舵舵偏角变化曲线。可以看出,5 m/s顺风扰动使图5中飞行速度骤减,升力减小,此时推油门以增大速度。-1 m/s的上扬风和1 m/s的下沉风对着舰俯仰角的影响较大,波动范围绝对值为0.5°左右,这是由于垂直方向的风产生突风迎角导致迎角变化,进而升力急剧变化,但是最终满足着舰条件[31]。结果表明,基于自适应动态逆的控制器能够在常值风干扰下,保持着舰下滑姿态以及飞行速度稳定。

3.2.2 舰尾流干扰环境

加入气动参数不确定性,并在无人机距舰船800 m时加入尾流干扰。由图8和图9可以看出无人机俯仰角能够渐近收敛于期望值。当遭遇舰尾流时,θ急剧变化,约5 s后θ在2°～3°范围内波动。触舰时无人机为抬头状态且俯仰角大于2°,满足着舰条件[31]。而未加入自适应控制时,θ跟踪性能急剧恶化,振荡幅度高达8°。结果表明当存在参数不确定性和外界风扰时,基于自适应动态逆的俯仰角控制器具有抗干扰和高精度跟踪能力。

图10为飞行速度变化曲线,初始时刻,动力补偿系统能够迅速补偿因参数不确定性以及无人机姿态调整产生的速度偏差,使V收敛于稳态值54 m/s,并以期望的下滑角沿轨迹线着舰(见图11)。当遭遇舰尾流时,即使在发动机通道带宽限制下,也能使V在期望值附近波动,跟踪误差范围为[-1.5,1] m/s。而在无自适应能力的速度控制下,产生20%左右的稳态误差。

由图12和图13可知,动力补偿系统通过调节δT大小来控制速度,遭遇舰尾流时,无人机受到的气动力和力矩急剧变化,进而导致升降舵和油门舵偏转量振荡。

4 结 论

针对存在参数不确定性的舰载无人机非线性模型,创新性地提出一种动力受限下的自适应动态逆着舰控制方法。利用动态逆的方法设计俯仰角和速度控制器,旨在解除系统多变量耦合,提高控制器动态响应速度。通过保持无人机俯仰角以及飞行速度稳定,实现对着舰下滑轨迹角的精确跟踪。并采用自适应控制策略对未知参数变化进行在线估计,保证控制器的跟踪性能,提高系统的鲁棒性。针对发动机通道动力受限时的自适应参数过度补偿问题,对自适应律进行修正,保证速度闭环系统的稳定性。仿真结果表明,着舰控制器具有较好的鲁棒性和跟踪性能。