低分辨率ADC下MIMO-OFDM系统中的广义Turbo信号检测

王华华, 李延山, 余永坤

(重庆邮电大学通信与信息工程学院, 重庆 400065)

0 引 言

毫米波通信与大规模多输入多输出(multiple input multiple output, MIMO)是两项关键的5G技术,由于毫米波的带宽分布于30～300 GHz,因此有望实现高速率通信。尽管这两项技术有高速率通信的潜力,但是传统方案往往需要非常高的采样频率才能够将接收到的模拟信号转化为数字信号。随着模数转换器(analog to digital converter, ADC)精度的提升,系统的开销和成本大大增加,功率的消耗也呈指数倍增长,尤其是在移动设备终端,功耗问题更是需要重点解决的问题。最近,带有低分辨率ADC的大规模MIMO在容量性能、信道估计、数据检测等方面引起了广泛关注。文献[14]中对加性高斯白噪声信道的容量推导表明,在低至2～3位的量化精度下,仅损失了10%～20%的容量。由于低分辨率ADC的硬件成本和实现复杂度相对较低,用较少的比特数表示数据存储和传输也更加容易,还能减轻整个链路其他组件的功耗问题。因此,一项可行的解决方案是在MIMO正交频分复用(orthogonal frequency division multiplexing, OFDM)量化系统的接收端使用低分辨率ADC。

MIMO技术与OFDM技术相结合为5G通信提供了标准的空中接口解决方案,称在MIMO-OFDM中引入低分辨率ADC的系统为MIMO-OFDM量化系统。低分辨率ADC量化会在接收信号中引入强烈的非线性失真,子载波之间的正交性会被破坏,造成严重的载波间干扰。这些问题给信号检测带来了不必要的麻烦,本文的主要目的就是解决低分辨率ADC给检测带来的问题。

学术界目前已经提出了多种从粗略量化结果中检测出发送信号的方法,包括线性接收机,基于投影梯度法的算法,基于快速自适应收缩/阈值算法的方法。消息传递方法,包括广义近似消息传递(generalized approximate message passing, GAMP)及其扩展双线性GAMP,矢量近似消息传递。这些算法都专用于一般的MIMO系统而非量化MIMO-OFDM系统中的信号检测问题。在文献[21-22]中,针对毫米波场景下的单输入单输出(single input single output, SISO)OFDM量化系统,提出了一种基于Turbo迭代原理的数据检测算法,该算法是一种计算易于实现且最优的SISO-OFDM检测算法。考虑到广义Turbo(generalized Turbo, GTurbo)算法在OFDM系统中良好的检测性能,因此将GTurbo算法运用到本文MIMO-OFDM系统中的信号检测问题。与SISO-OFDM系统相比,MIMO-OFDM系统中接收端每根天线上的信号是由所有发送信号经过信道之后叠加得到的,因此检测问题的困难在于如何从接收信号中将发送信号解耦合出来。本文考虑在每个子载波上对接收信号重排列,用滤波矩阵的方式将发送信号解耦合出来,进而实现GTurbo算法在MIMO-OFDM系统中的低复杂度实现方案。

符号说明:对于矩阵,,和分别表示求矩阵的伪逆、转置和共轭转置。对于列向量,用diag{}表示由的元素构成的对角矩阵。特别地,表示零向量,表示单位矩阵。对于一个复数标量,用和分别表示的实部和虚部。

1 系统模型

考虑一个具有个正交子载波的量化MIMO-OFDM系统,该系统配有根接收天线和根发送天线,在每根接收天线处均配备有一个低精度复值量化器(·),量化器的精度为1～3 bit。

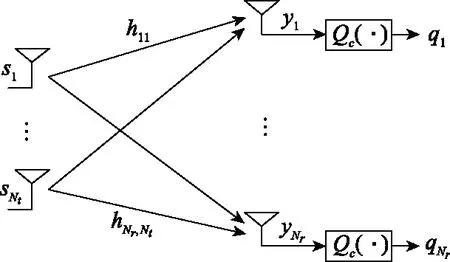
图1 量化MIMO-OFDM系统模型Fig.1 Quantization MIMO-OFDM system model

用=[,,…,]∈×1表示每根天线上发送的复值符号序列,表示所选用调制方式的星座点集。例如,当采用四进制正交幅度调制时,星座点集为

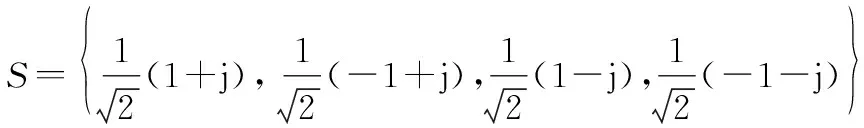
(1)

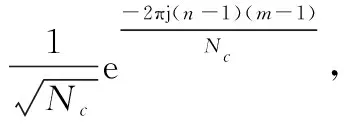
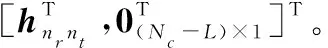
在第根接收天线处,去掉CP之后的未量化接收信号表示为

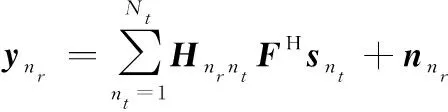
(2)

=

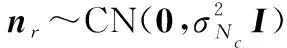
(3)

进而,未量化的接收信号可表示为

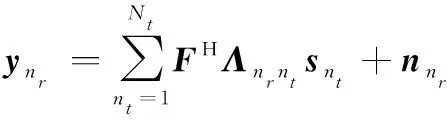
(4)

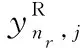
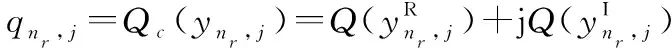
(5)

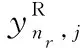
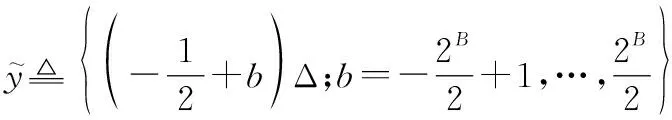
(6)

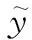
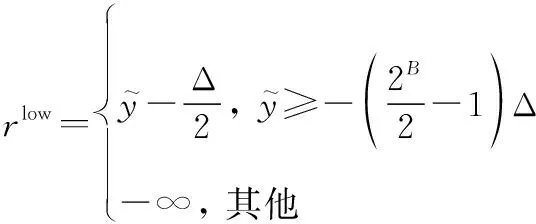
(7)

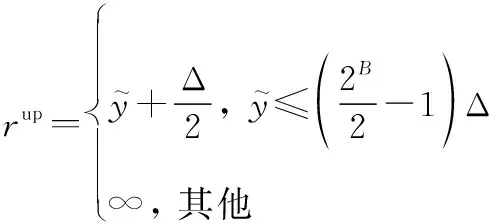
(8)

量化后的接收信号可表示为

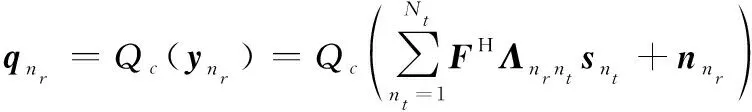
(9)

=(+)

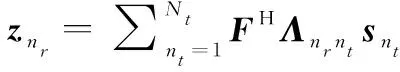
(10)

为了不失一般性,用=(+)表示量化模型,信号检测的目的就是从量化信号中恢复出发送的符号序列。

2 GTurbo-M算法

GTurbo-M算法如下。

GTurbo-M算法

,

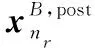
1初始化:

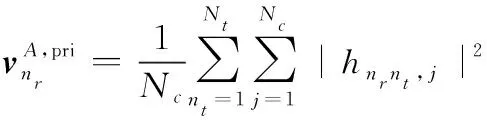
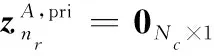
2从=1:循环以下计算:

模块A:

(1) 步骤1:计算的后验均值和方差

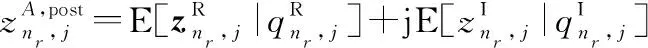
(11a)

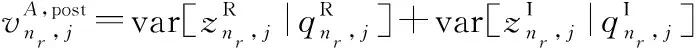
(11b)

(2) 步骤2:计算的外部均值和方差

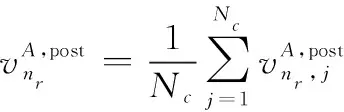
(12a)

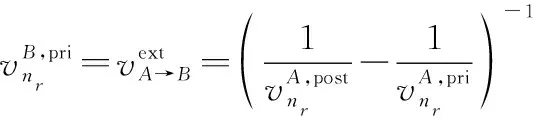
(12b)

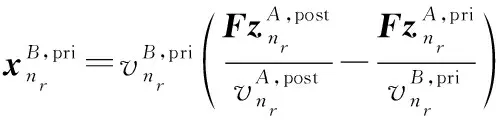
(12c)

模块B:

(3) 步骤1:计算的后验均值和方差

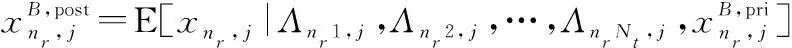
(13a)

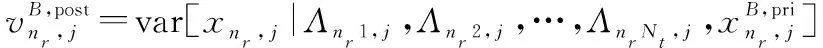
(13b)

(4) 步骤2:计算的外部均值和方差

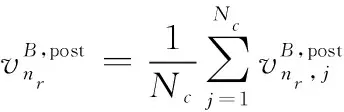
(14a)

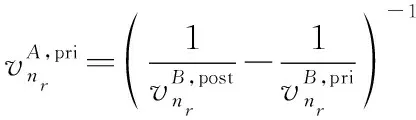
(14b)

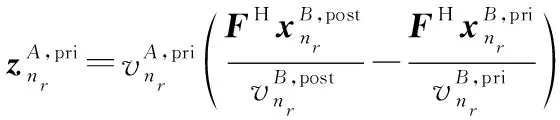
(14c)

文献[22]在SISO-OFDM量化系统中提出了一种基于GTurbo算法的检测器,在该系统中GTurbo检测器能实现贝叶斯最优数据检测,且计算复杂度不高。由于GTurbo检测器在量化OFDM系统中的优势,因此考虑将该算法应用于MIMO-OFDM量化系统,并提出了基于GTurbo-M算法的GTurbo-M检测器。

2.1 GTurbo-M检测器的设计原理

MIMO系统接收端在得到量化信号之后,每根接收天线均执行相同的操作,以第根接收天线上的量化信号为例阐述GTurbo-M检测器的设计原理。该检测器由3部分构成,分别是时域检测器模块A、频域检测器模块B和解耦合模块C。外部信息交换在模块A和B之间以Turbo方式迭代进行,直到算法收敛,解耦合模块C用于降低矩阵和向量的维度。

首先定义两个中间矢量信号方便后续推导:

=

(15)

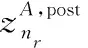
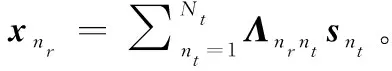
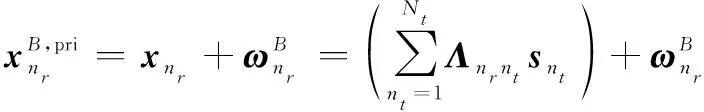
(16)

对模块B得到的频域估计值堆叠后有

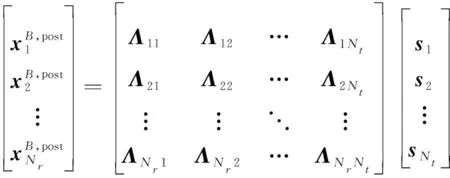
(17)

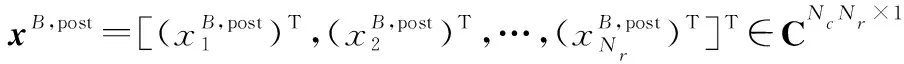
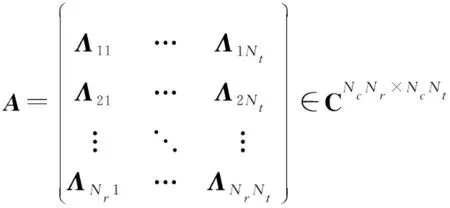
表示所有天线对之间的频域信道矩阵。

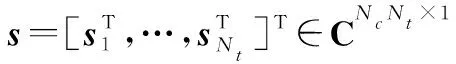
在估计出,post后,可以对发送信号按照式(17)进行估计,该估计问题本质上是一个线性估计问题,因而可采用基于MMSE和迫零(zero forcing, ZF)的估计方法,而基于MMSE和ZF估计的计算复杂度主要集中在矩阵求逆部分。若直接对式(17)采用MMSE估计,则整体计算复杂度为(())。显然，在大系统中这样的计算复杂度不符合实际应用的预期要求,因此设计了模块C用于降低矩阵和向量的维度。

由于频域信道矩阵实质上是对角矩阵,因此解耦合模块C考虑在子载波上对估计信号进行重排列,具体如下:

式(17)在第(∈{1,2,…,})个子载波上的对应关系式为

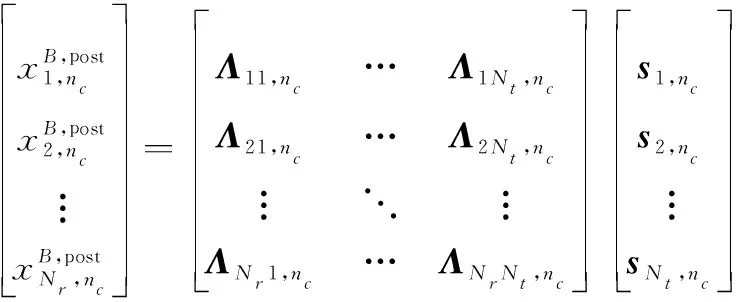
(18)

式中:

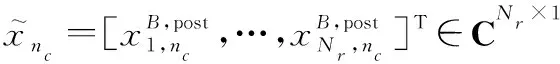
(19)

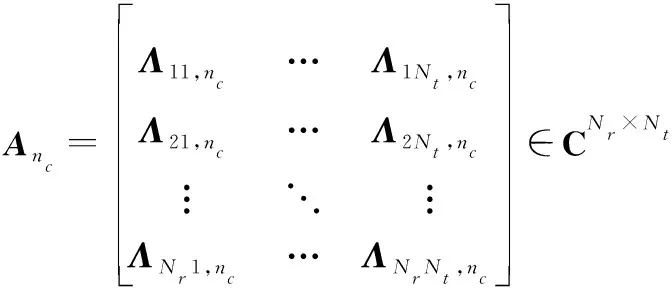
(20)

=[1,,…,,]∈×1

(21)

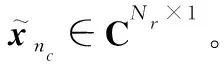
在大系统中,子载波的数量往往远大于接收天线的数量。通过GTurbo-M检测器,不仅能得到频域估计值,post,还通过增加矩阵个数的方式降低了矩阵的维度,减小了矩阵求逆的复杂度,达到整体复杂度下降的目的,原理框图如图2所示。

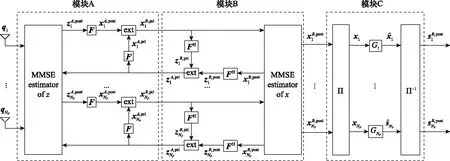
图2 GTurbo-M检测器框图Fig.2 Block diagram of GTurbo-M detector

2.2 GTurbo迭代算法

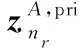
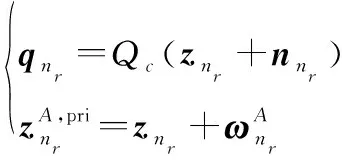
(22)

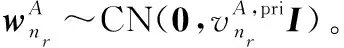
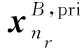
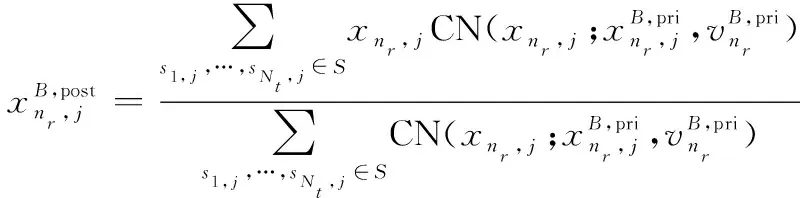
(23)

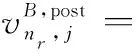
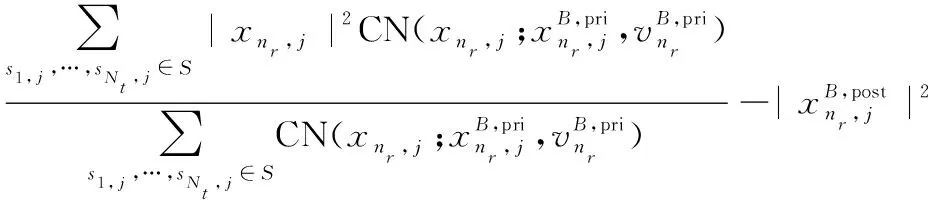
(24)

式中:, =1, 1, +…+, , 。

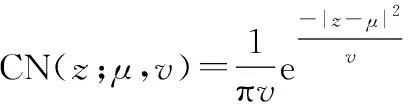
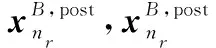
2.3 解耦合模块C

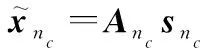
(25)

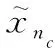
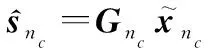
(26)

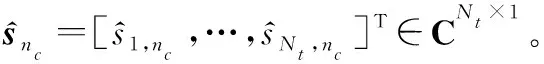
产生滤波矩阵的常用的方法有ZF串行干扰消除(ZF-successive interference cancellation, ZF-SIC)算法、和MMSE串行干扰消除(MMSE-successive interference cancellation, MMSE-SIC)算法。ZF-SIC算法能最大限度地滤除不同天线之间的信号干扰,且实现简单,MMSE-SIC算法能够平衡信道噪声项对检测的影响,在高信噪比条件下MMSE-SIC性能更优。

本文分别采用ZF-SIC和MMSE-SIC算法产生不同的滤波矩阵,并在仿真结果中对基于不同滤波矩阵的GTurbo-M检测器性能进行了比较。

3 计算复杂度分析

此外,代表信号重建算法的GAMP算法的复杂度为3,表示算法的迭代次数,GAMP算法一般在10次迭代左右收敛。

因此,特别是在多载波和低阶调制的场景下,GTurbo-M算法实现的计算复杂度比GAMP算法小得多,在下一节中将比较GAMP算法和GTurbo-M算法的误比特率(bit error ratio, BER)性能。

4 BER性能分析

假设在发送端,发送序列中的每个传输符号(∈{1,2,…,})均满足E[]=0,且符号能量为=E[||]=1。

为了分析量化系统中的BER性能,本文参考了文献[25]中提到的加性量化噪声模型(additive quantization noise model, AQNM),借助AQNM模型,第根接收天线上的量化信号可以改写成

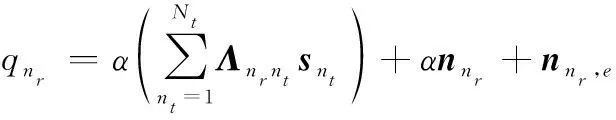
(27)

式中:,∈×1表示与不相关的加性量化噪声;表示与量化比特数相关的失真因子,具体取值可见表1,联合式(15)和式(27),得到

表1 失真因子与量化精度的对应关系

=α+α+,

(28)

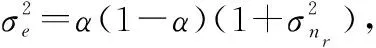
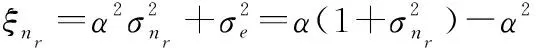
(29)

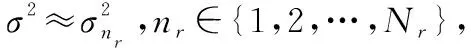
≈=(1+)-

(30)

结合文献[25]和已有的知识,采用正交相移键控调制时,理论BER为

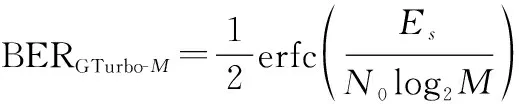
(31)

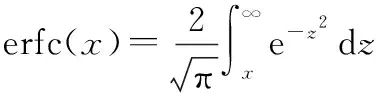
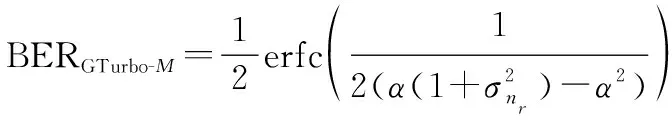
(32)

实际系统中的BER性能由接收端解调出来的错误比特数与传输的总比特数的比值决定,即

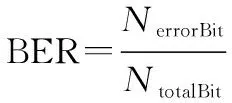
(33)

5 仿真结果分析

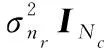
图3是在2发4收MIMO场景下3种检测器的BER性能图。从图3中可以看出,在相同量化精度下,基于GTurbo-M的检测器均比GAMP检测器的BER更小,且二者之间的差距随着量化精度的提升逐步扩大,在信噪比为21 dB时,GTurbo-MMSE-SIC检测器就能达到10的BER,而GTurbo-ZF-SIC检测器在23 dB才能达到同样的误比特率。同时也可以看出,在1 bit量化精度条件下,3种检测器的BER曲线变化缓慢,这是因为在1 bit时,量化器非线性失真严重,仅能保留接收信号的符号,幅度信息损失严重。因此,在这种条件下,3种检测器的检测性能都比较差。

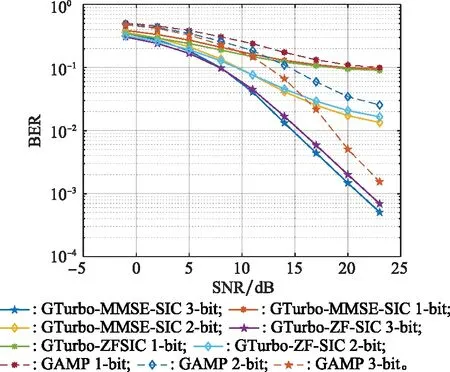
图3 2×4 MIMO-OFDM系统中BER性能Fig.3 BER performance in 2×4 MIMO-OFDM systems

图4是在4发32收MIMO场景下3种检测器的BER性能图,图3与图2反映出的结果基本一致,BER性能随量化精度增加而提升,但是随着接收端天线阵列规模的增加,可以明显看出3种检测器的BER变化曲线更陡峭。

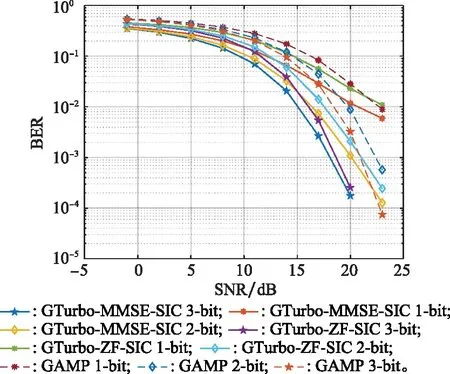
图4 4×32 MIMO-OFDM系统中BER性能Fig.4 BER performance in 4×32 MIMO-OFDM systems

同在GTurbo-M算法下,GTurbo-MMSE-SIC检测器比GTurbo-ZF-SIC检测器的性能更好,当BER为10和量化精度为3 bit时,前者性能提升约1 dB。在不同算法下,基于GTurbo-M的两种检测器在18 dB附近达到10的BER,而基于GAMP的检测器要在21 dB左右才能达到同样的性能。

6 结 论

基于GTurbo-M算法的检测器在配备有低分辨率ADC的MIMO-OFDM量化系统中具有良好的检测性能,随着天线阵列规模增大和量化精度增加,检测性能逐步提升。同时仿真结果表明,无论是量化器在1 bit,2 bit还是3 bit的量化精度下,基于GTurbo-M的检测器的BER性能均比GAMP检测器好,且量化精度越高,二者之间的差距越大。

但是,GTurbo-M算法在天线规模增大之后,计算复杂度随检测性能同步增加,特别是发送端天线规模,每增加一根发送天线,计算复杂度要增加倍。因此,检测器在实际的MIMO-OFDM量化系统中应用时,要考虑天线规模与检测性能的折衷,要根据BER、信噪比和量化器的量化精度要求来动态调整天线阵列的规模。