SR-CH∞KF用于弹丸飞行姿态测量研究

张平安, 汪 伟,*, 高 敏, 王 毅

(1. 陆军工程大学石家庄校区火炮工程系, 河北 石家庄 050084; 2. 陆军工程大学石家庄校区导弹工程系, 河北 石家庄 050084)

0 引 言

弹丸飞行姿态估计的目标是确定物体固定坐标的方向相对于导航坐标系的方向。由于姿态估计问题本质上是一个非线性滤波问题,于是许多非线性滤波方法被提出。非线性滤波中比较具有代表性的有扩展卡尔曼滤波(extended Kalman filter,EKF)、无迹卡尔曼滤波(unscented Kalman filter,UKF)以及容积卡尔曼滤波(cubatu Kalman filter, CKF)。EKF围绕滤波值将非线性状态过程和量测模型展开成泰勒级数并省去二阶以上的项,得到一阶近似线性化模型,然后根据线性卡尔曼滤波原理对系统进行滤波处理。这种方法的前提是非线性函数具有现实的表达式且存在偏导数。一阶近似得到的Jacobian矩阵与实际模型之间存在误差,在系统模型传递过程中误差会出现累积现象,导致最后计算值的发散。Julierder等人摒弃了对非线性函数进行线性化的传统做法,采用无迹变换(unscented transform,UT)对非线性函数的概率密度分布近似的方法来处理均值和协方差的非线性传递问题,提出了UKF的算法。与UKF相似,CKF利用球面径向规则来逼近非线性函数的概率密度分布。虽然UKF和CKF来自不同的数学观点,但可从几个方面进行比较。两者都使用确定性的Sigma点来获取均值和协方差,UKF需要2+1个Sigma点,而CKF需要2个容积点。UKF需要附加一个与状态维数有关的缩放参数,而CKF在采样的过程中不需要其他参数的加入,无论状态维数为多少,始终可以保持权值为正值,使得滤波能够顺利进行下去。因此,CKF比UKF在高维系统状态估计中有更好的应用。

标准的CKF算法经过多次递推,计算的舍入误差会逐渐累积,导致误差协方差矩阵失去对称性和正定性,这种累积误差最常出现在弹丸的姿态测量中。近年来,许多学者针对这一现象进行了大量的研究。其中,Qiu在标准的CKF中引入了基于多重强跟踪的自适应Huber算法,可以有效改善CKF的滤波性能;Geng通过建立基于预测残差构造的自适应因子来克服CKF模型误差和异常干扰的影响;Tang利用矩阵的奇异值分解(orthogonal decomposition, QR)和四元数数值积分构建新的CKF算法,有效提高了滤波的收敛速度;Huang为了提高CKF的调节能力,提出了一种稳定的高强跟踪CKF算法。对此,为了减少滤波运算过程的复杂度,应用了数值稳定性较强的QR方法,可以有效分解系统状态协方差矩阵并进行迭代,提高了算法运算过程中的数值稳定性。H∞滤波是假设在噪声干扰环境最坏的情况下建立的线性状态估计方法,适用于系统过程噪声和量测噪声统计特性未知的状态估计问题,同时对系统建模不准确有一定的适应能力。本文提出了一种全新的基于H∞滤波改进的SR-CKF算法,将H∞滤波的鲁棒性优势与SR-CKF在非线性系统上的高精度处理能力相结合,利用三轴地磁传感器和陀螺仪组合系统对弹丸的飞行姿态进行解算。

本文提出了一个新颖的基于H∞滤波的姿态估计算法,有效提高了算法的鲁棒性和滤波精度。与文献[22]相比较,本文提出了自适应的误差补偿参数计算并降低了滤波运算的复杂度。具体而言,本文的贡献在以下几个方面:① 在线性-非线性系统中,将H∞滤波融入到SR-CKF中,建立了平方根容积H∞滤波(SR-CH∞KF);② 在SR-CH∞KF中采用了欧拉角测量模型,利用线性状态方程减轻了计算量;③ 从Silbley等人的工作中提取了误差协方差矩阵和互协方差矩阵的近似方法,将线性状态的H∞滤波成功地转化到了非线性系统。此外,受这种方法启发,详细推导了误差协方差矩阵和量测噪声的更新表达式。

1 传感器配置和姿态测量模型

1.1 坐标系与传感器配置

由于弹丸是对称构建,弹丸的重心在弹轴上,因此传感器安装在弹轴位置处,陀螺仪和地磁传感器呈前后位置安装,安装示意图如图1所示。

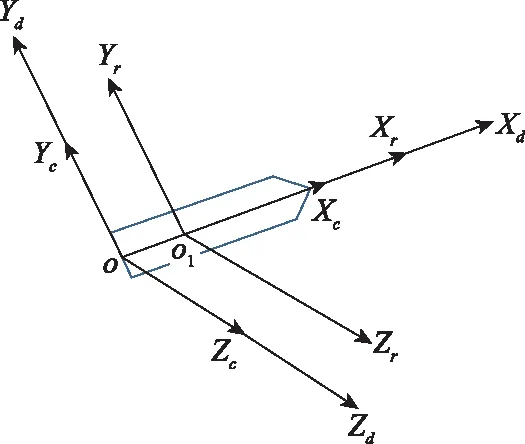
图1 传感器的安装方式Fig.1 Installation method of sensor

图1中,-为载体坐标系,-为地磁传感器坐标系,1-为陀螺仪坐标系。、和在安装时与弹轴方向保持一致,与在安装时保持平行,和在安装时保持平行。为了更好地去表示弹丸在飞行过程中的飞行姿态,选用北天东坐标系作为导航坐标系,用、和去表示坐标系的北轴、竖直轴和东轴。

1.2 陀螺仪模型

弹丸在飞行过程中的姿态变化用弹丸在北-天-东坐标系的俯仰角、偏航角以及滚转角进行表示,其中俯仰角是弹轴与水平面的高低夹角,用表示;偏航角是弹轴在水平面的投影与北轴的夹角,用表示;滚转角是弹丸绕着自身弹轴翻滚的角度,用表示(3个姿态角的正负都满足右手定则)。弹丸在飞行过程中的任一姿态都可以用图2的示意图进行表示。

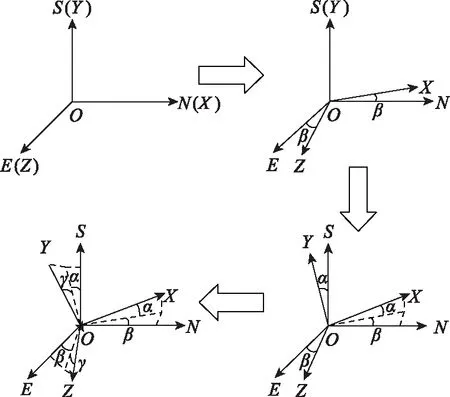
图2 坐标系转换方式Fig.2 Coordinate systems conversion mode

在图2中,弹丸任一姿态的起初都可以看作是载体坐标系与北天东坐标系完全重合,然后绕着轴旋转角,绕着轴旋转角,绕着轴滚转角。

陀螺仪在弹丸飞行过程中能够测量出弹丸在载体坐标系中的3个角速度,分别用、和表示(3个角速度的正负满足右手定则),其中是轴和轴绕着轴旋转的角速度,是轴和轴绕着轴旋转的角速度,是轴和轴绕着轴旋转的角速度。陀螺仪测得的3个角速度与飞行器的姿态角速度的关系可以通过欧拉角微分方程得到,如下所示:

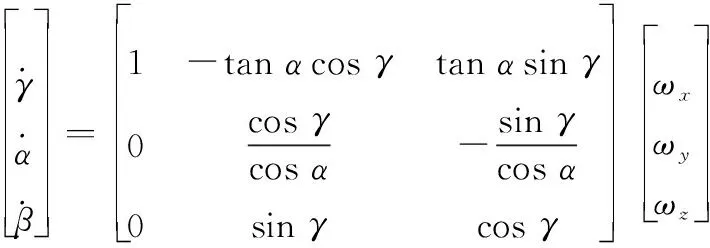
(1)

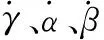
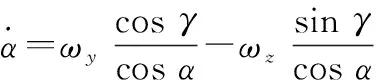
(2)

(3)

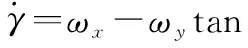
(4)

对俯仰角速度、偏航角速度和滚转角速度进行数值积分可以得到俯仰角、偏航角以及滚转角,用数学模型表示为

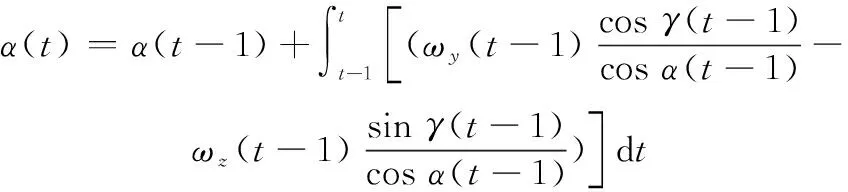
(5)

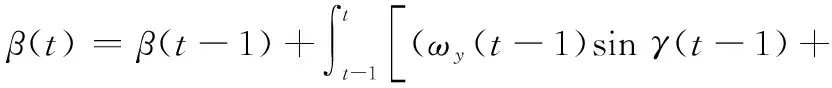
(6)

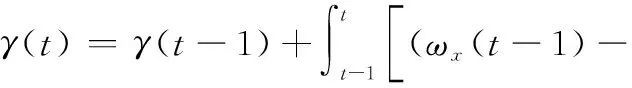
(7)

由于弹丸的滚转速度较大,会超出陀螺仪测量的量程,因此陀螺仪的轴在弹丸飞行过程中处于断路状态。陀螺仪测量计算俯仰角和偏航角中所需要的前一时刻滚转角由地磁传感器测量获得。

1.3 地磁传感器模型

地磁场作为地球的基本能量场,是地球的一种重要固有资源,近地面任意地点的地磁强度由地磁要素决定,地磁要素由经度、纬度和海拔高度组成,为地磁导航提供了良好的测量基准。根据发射位置的经度、维度和高度,通过世界地磁场模型可以解算得到地磁矢量在北-天-东坐标系中的磁倾角和磁偏角,进而得到地磁矢量在北-天-东坐标系3轴的分量、和,如下所示:

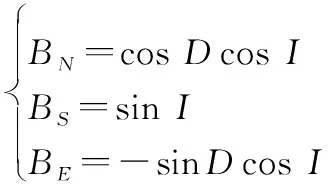
(8)

式中:为弹丸发射处的地磁强度;和分别为磁偏角和磁倾角,磁倾角以水平面上方为正,磁偏角以北偏西为正。由图2所示的坐标系转换方式可知,弹丸飞行过程中载体坐标系与导航坐标系的关系可以表示为

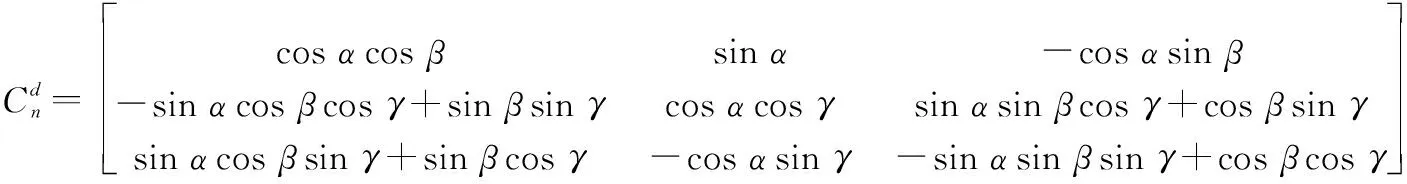
(9)

弹丸飞行过程中地磁矢量在载体坐标系3轴的投影可以表示为

=coscoscos(-)+sinsin

(10)

=-cossincoscos(-)-
cossinsin(-)+sincoscos

(11)

=cossinsincos(-)-coscos·
sin(-)-sincossin

(12)

由于地磁传感器坐标系与载体坐标系完全重合,即=,=,=。由和之间的比值关系,可以得到滚转角的解析式为

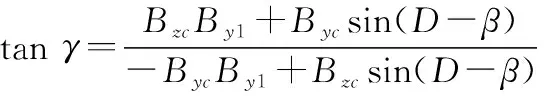
(13)

式中：1=tancos-sincos(-)。

在地磁传感器测量弹丸飞行滚转角时,同时要利用地磁传感器计算的弹丸滚转圈数,计算圈数在文献[24]中进行了详细说明。由于滚转角的范围在0°到360°之间,而反正切求值的范围在-180°到180°之间,因此需要引入其他变量对滚转角的求解范围进行重定义。滚转角是弹丸绕着自身弹轴滚转的角度,可以看成是载体坐标系的轴绕着弹轴转过的读数,滚转角可以用象限来进行判断大小,如图3所示。

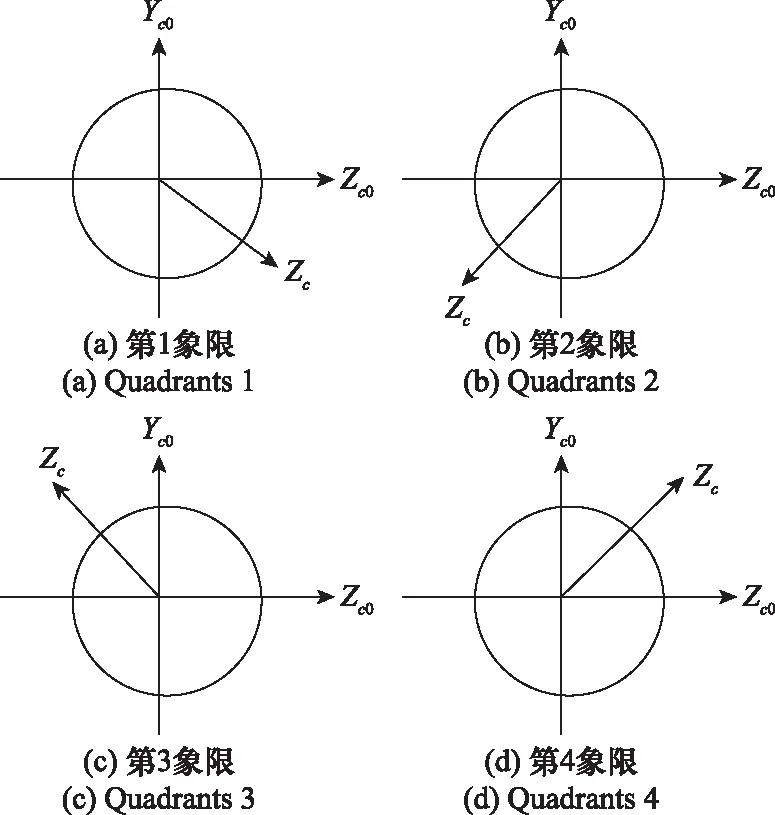
图3 滚转角象限示意图Fig.3 Diagram of rolling angle quadrants

在图3中,0和0是滚转角为0时地磁传感器轴和轴的位置。图3(a)～图3(d)分别表示了滚转角的范围为0°～90°、90°～180°、180°～270°和270°～360°,用数学表达式可以表示为

(1)<0,>0,=+360°;

(2)<0,<0,=+90°+360°;

(3)>0,<0,=+180°+360°;

(4)>0,>0,=+270°+360°;

式中：为实际滚转角的大小;为测出弹丸滚转的圈数;是由式(13)直接解出,用数学模型可以表示为

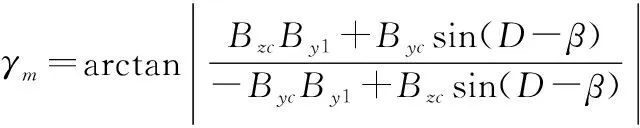
(14)

2 基于线性-非线性系统的SR-CKF运用

在实际工程应用容积卡尔曼滤波算法时,由于计算机字长有限,可能导致以下结果:误差协方差矩阵将失去对称性和正定性,以及过滤器的数值稳定性会受到较大影响。平方根容积卡尔曼滤波可以避免直接操作误差协方差矩阵,采用矩阵的QR分解法,可较大提高过滤器的稳定性,在较大程度上改善滤波在线性-非线性测量系统中的性能。

针对陀螺仪/地磁传感器姿态测量系统中获得的俯仰角和偏航角,利用式(5)、式(6)和式(10)建立状态方程和量测方程:

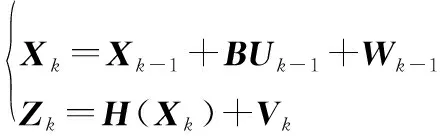
(15)

式中:∈为×2维的系统状态向量;∈为×1维的量测向量;-为输入控制矩阵;为控制输入矩阵;(·)为非线性函数,-1和分别为状态系统和观测系统的均值为0,协方差分别为-1和的高斯白噪声,且相互独立。

线性-非线性系统的SR-CKF算法如下。

(1) 系统初始化

初始俯仰角和偏航角由飞行器发射姿态决定,初始误差协方差由实际发射条件决定;

(2) 计算点集和均值

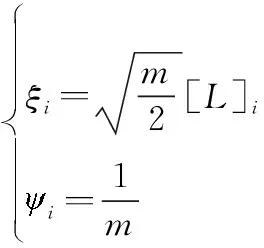
(16)

式中：=0,1,2,…,,表示基本容积点个数,根据三阶球面径向容积准则,容积点数是状态变量维数的2倍,即=2,为状态变量维数;[]表示完整全对称点集,由于状态变量为俯仰角和偏航角,则=2,可以得到点集中的第个元素为

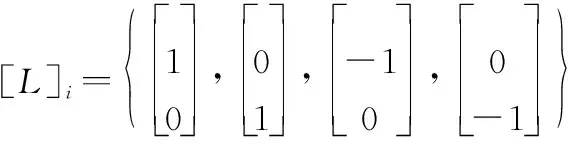
(3) 时间更新

① 计算容积点:

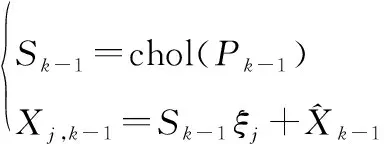
(17)

式中:Chol表示矩阵的Cholesky分解。

② 传播容积点,计算状态方程后的估计值:

,|-1=,-1+-1-1

(18)

③ 预测状态变量,计算加权后容积点估计值的和:

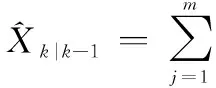
(19)

④ 估计误差协方差阵平方根系数,三角分解:

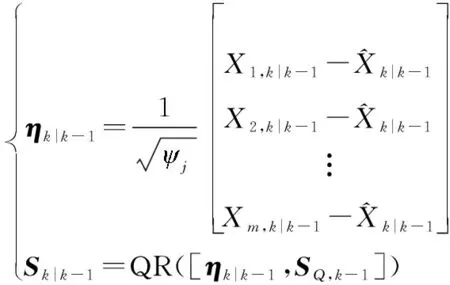
(20)

式中:QR(·)表示通过矩阵的QR分解得到的下三角矩阵;,-1是状态系统噪声的协方差矩阵-1经过Cholesky分解得到的矩阵。

(4) 测量更新

① 传播量测容积点,计算量测方程的估计值:

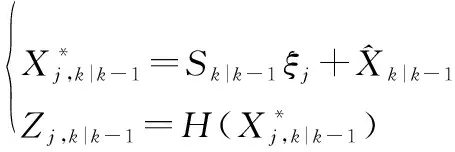
(21)

② 量测预测,容积点预测值的加权和:

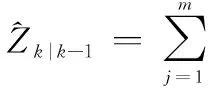
(22)

③ 计算新息协方差矩阵,三角分解:

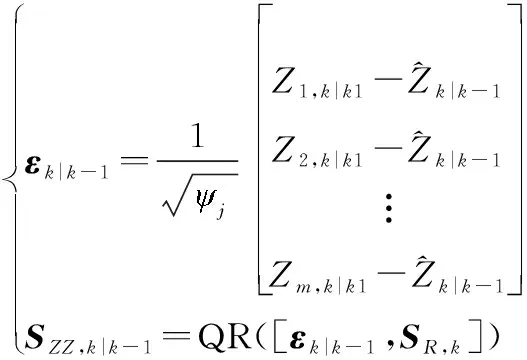
(23)

式中:,是状态系统噪声的协方差矩阵经过Cholesky分解得到的矩阵。

④ 计算互协方差矩阵:

(24)

⑤ 计算SR-CKF滤波增益值:

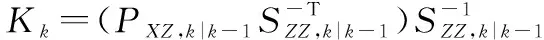
(25)

⑥ 计算状态变量估计值,根据量测值更新状态值:

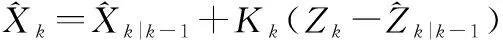
(26)

⑦ 更新误差协方差矩阵平方根系数,矩阵的正交三角分解:

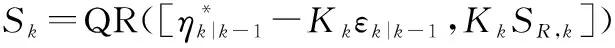
(27)

3 H∞滤波与SR-CKF结合估计飞行姿态

3.1 H∞滤波基本原理

通过引入H∞范数思想的方法,可以有效解决H∞滤波中的系统模型及噪声统计特性的不确定性,同时可以保证干扰输入到滤波输出的过程中H∞范数的最小化,达到即使在最坏情况下系统的估计误差也能保证最小化的目的。

定义下式所示的代价函数为

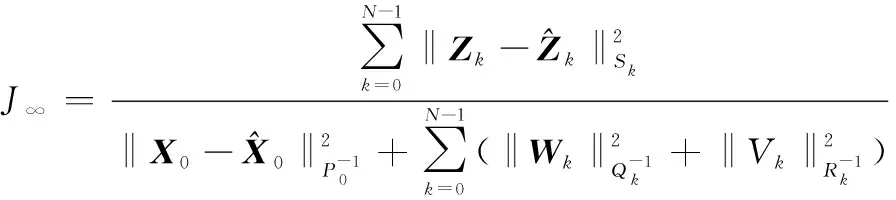
(28)

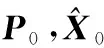
a。

H∞滤波器是为了使状态估计误差最小,通常情况下,最优H∞滤波问题存在一个较大的缺陷是最佳解析形式的解很难获得,因此寻求一种新的高效迭代算法,∞的边界由、和在最坏情况下设计规定一个门限值:

sup∞<

(29)

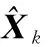
在H∞滤波器中,为了使滤波器的问题有解,在每一时刻必须满足下式所示的不等式,即Riccati不等式:

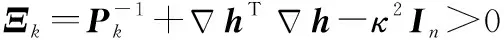
(30)

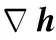
在H∞滤波器中,误差限定参数可以实现控制估计误差,即使状态估计在最坏情况下,的取值与系统的鲁棒性成反比。同时当的取值达到一定范围时,H∞滤波器与标准的卡尔曼滤波的滤波特性相似。常规的误差限定参数是根据实际工程经验设置为具体值,从而使滤波效果存在着很大的保守性,无法适应随时发生变化的弹丸飞行环境,不能同时实现降低系统估计误差及提高系统鲁棒性。因此,需要对误差限定参数的取值进行自适应选取。

由于新息序列的平方和在提高滤波器的性能方面与误差限定参数成反比,为了能够实现连续解算误差限定参数,引入了新息序列。新息序列的解算方法为

(31)

根据矩阵不等式相关理论可以引入一个定理:设和为2个阶的Hermite矩阵,>0,≥0,则>⟺(<1)。这里()表示的最大特征值。根据定理由Riccati不等式可以得到:

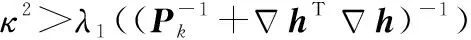
(32)

进而可以得到误差限定参数的值为

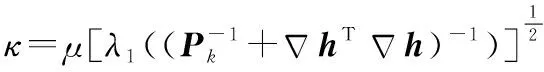
(33)

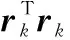
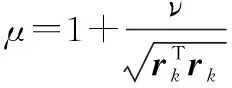
(34)

3.2 容积H∞滤波

将H∞滤波融入容积卡尔曼滤波,形成容积卡尔曼H∞滤波器(CH∞F)。在CH∞F过程中,时间预测阶段与CKF类似,包括误差辅助矩阵的因子分解、估计容积和容积点传播以及状态预测和误差协方差矩阵的预测。由于量测方程为非线性方程,则需要借鉴EKF的方法,利用雅可比矩阵将非线性方程近似转化为线性方程进行求解,H∞滤波的量测更新阶段的更新状态和量测更新协方差矩阵可表示为

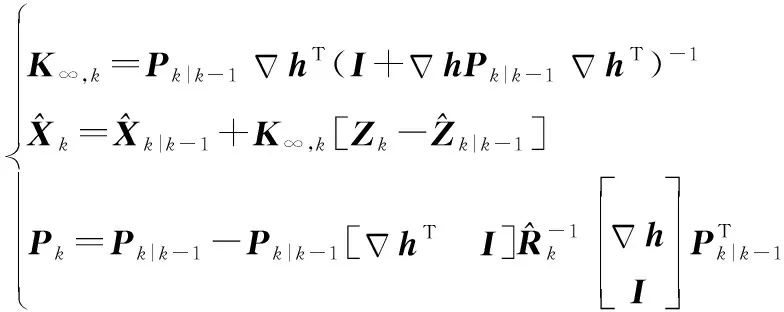
(35)

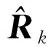
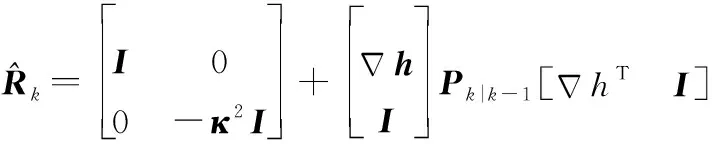
(36)

Sibley等人利用雅可比矩阵将非线性转化为线性的方法,提出了基于线性误差传播特性的误差协方差和互协方差近似方法:

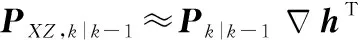
(37)

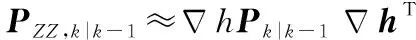
(38)

利用式(36)和式(37),对式(35)中部分进行变化:

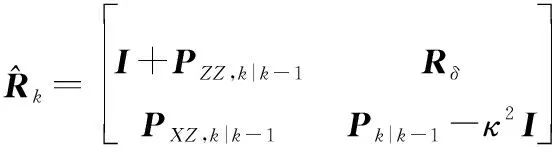
(39)

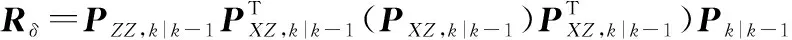
更新协方差矩阵可以转化为

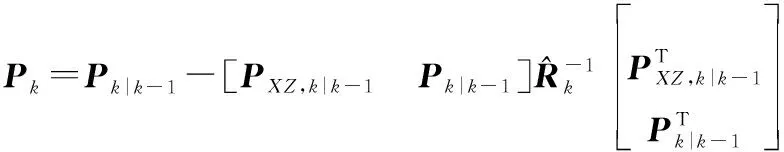
(40)

将式(37)和式(38)代入式(25),可以得到增益值的更新方程为

∞,=,|-1[,|-1+]

(41)

3.3 SR-CH∞KF滤波

将上述的增益值更新、状态值估计和误差协方差估计带入到平方根容积卡尔曼滤波的滤波步骤中可以得到平方根容积H∞滤波。

在进行判断之前,首先按照式(37)将噪声误差估计值进行解算,然后根据式(38)和式(40)对式(30)中的Riccati不等式进行转化,得到:

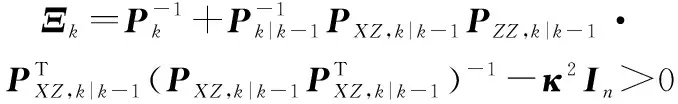
(42)

根据实际情况选取合适的误差限定参数后,进行测量更新计算。计算SR-CH∞F滤波增益值的解析式如式(41)所示,状态更新值计算可以参照式(35)进行计算,误差协方差矩阵更新可以参照式(39)和式(40)进行解算。

SR-CKF算法中的和,可以用H∞滤波系统中的滤波增益值和误差协方差矩阵递推式进行替代,并进行量测噪声的不断更新,构成了基于H∞滤波的SR-CKF算法,流程图如图4所示。

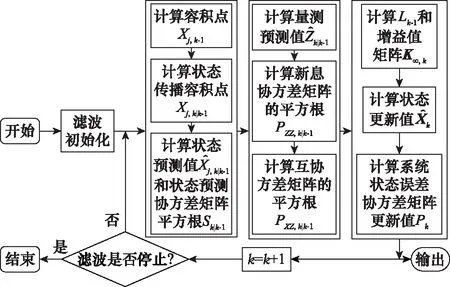
图4 SR-CH∞KF流程图Fig.4 SR-CH∞KF flow chart

4 仿真校验

为了验证SR-CH∞KF在线性-非线性系统估计问题的性能,我们采取了仿真实验的方式,利用弹丸实际飞行轨迹数据作为理论真值,用理论真值加上量测噪声作为地磁传感器X轴的量测输出值。在仿真实验之前,必须要知道仿真发射地点的经度、纬度以及海拔高度,以成都某地为例,经度为30.67°,纬度为104.07°以及海拔高度为523.87 m,利用基于国际地磁学和高空物理协会(International Association of Geomagnetism and Aeronomy,IAGA)给出的最新国际地磁参考场(International Geomagnetic Reference Field,IGRF),得到如表1所示的地磁参数。

表1 地磁参数

弹丸需要对发射速度和发射姿态进行确定,同时在姿态测量中,陀螺仪也需要输入初始姿态才能进行后续姿态解算。因此在仿真实验中,也需要对初始条件进行首要确定,仿真实验的初始条件如表2所示。

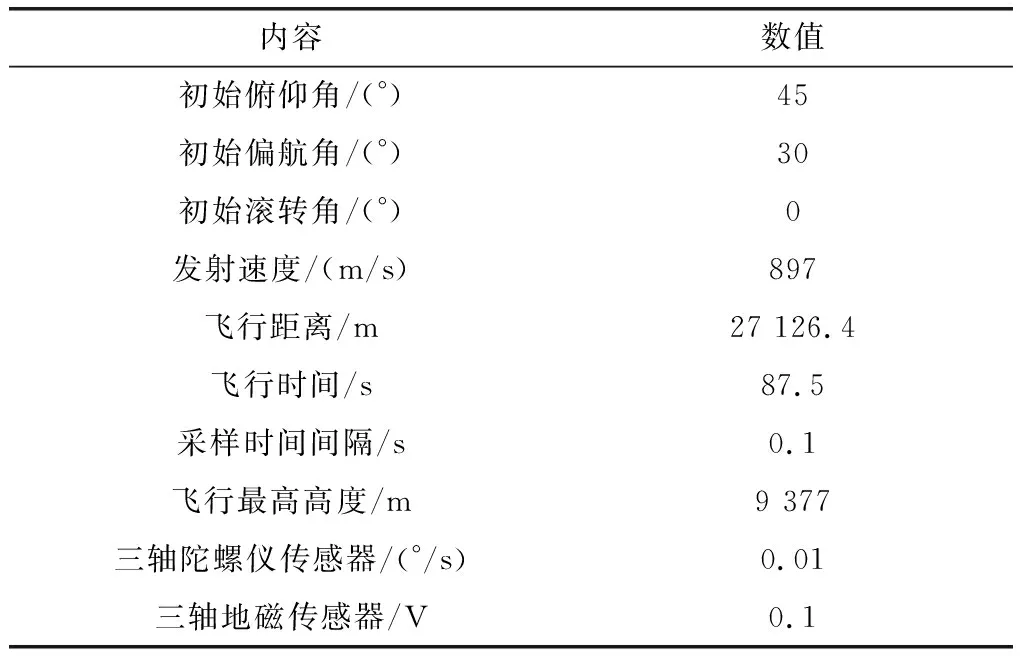
表2 仿真条件

为了更加直观了解SR-CH∞KF的精确性,我们分别计算了容积卡尔曼滤波和平方根容积卡尔曼滤波算法的性能作为对比。图5中蓝色代表经过CKF后的俯仰角误差变化曲线,黑色代表经过SR-CKF后的俯仰角误差变化曲线,红色代表经过SR-CH∞KF后的俯仰角误差变化曲线。经过观察3种滤波后的俯仰角误差范围,可以知道CKF的滤波效果在3种滤波中是最差的; SR-CKF误差变化曲线波动较大,但是比CKF的精度高;3者之中,SR-CH∞KF关于俯仰角的滤波精度最高。

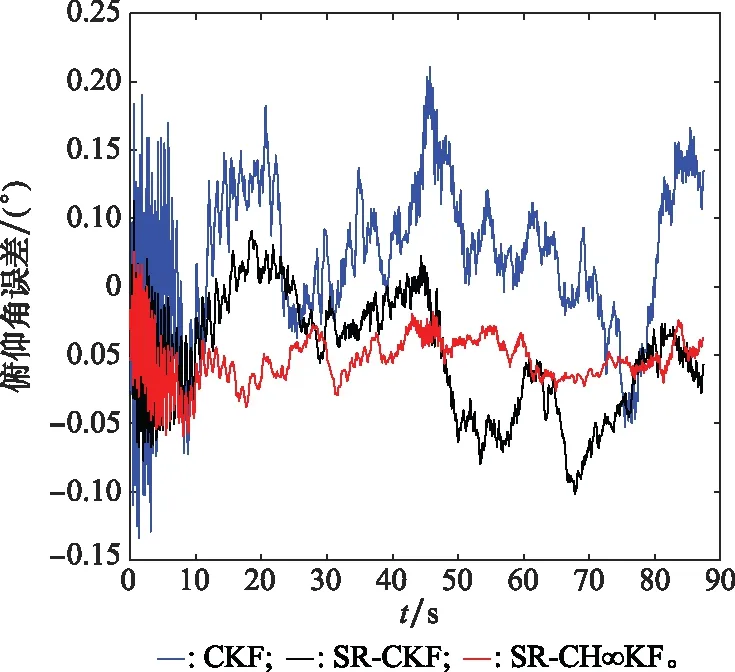
图5 俯仰角误差对比示意图Fig.5 Schematic diagram of pitch angle error comparison

图6中的曲线颜色代表的滤波种类和图5相同,通过观察偏航角误差对比示意图,可以发现CKF的滤波效果最差,SR-CKF的误差变化曲线在前期波动较大,后期的误差曲线较为平稳;SR-CH∞KF的滤波曲线较为平稳,并且相比较于其他两种滤波,滤波精度较高。

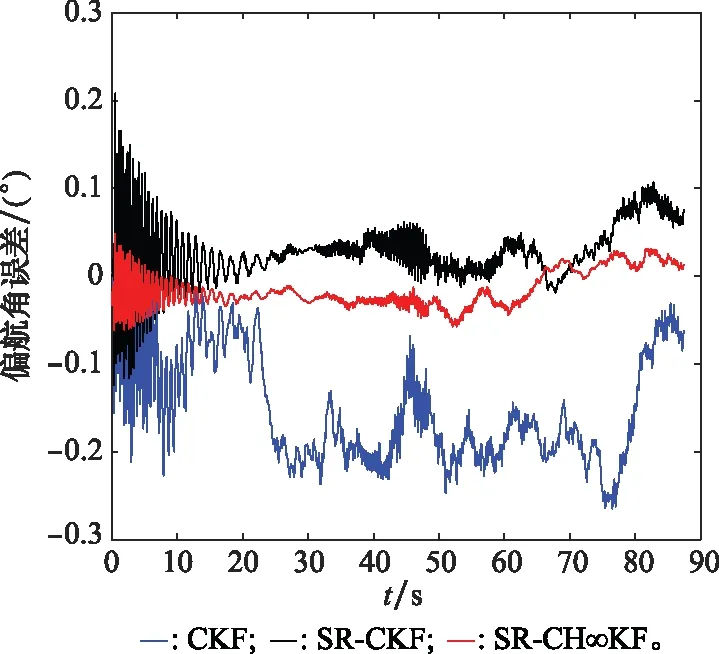
图6 偏航角误差对比示意图Fig.6 Comparison diagram of yaw angle error

图7中的曲线颜色代表的滤波种类和图5中相同,在60～80 s内由于收到地磁盲区的影响,使滚转角的误差较大,但是从图6可以看出,SR-CH∞KF可以有效地降低磁测量盲区的滚转角测量误差。在非盲区范围内, SR-CH∞KF的滤波精度相对较高。从整体的滚转角测量误差变化来看,可以知道SR-CH∞KF对于滚转角的滤波精度较高。

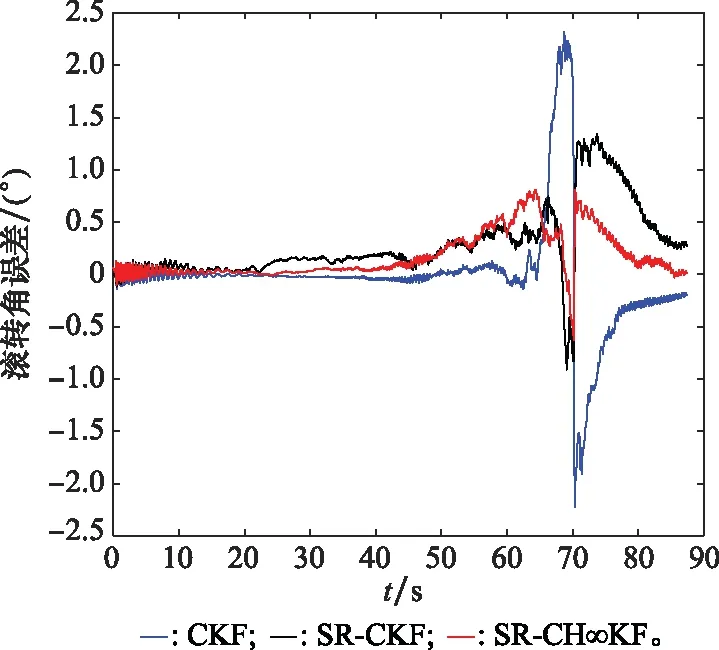
图7 滚转角误差对比示意图Fig.7 Comparison diagram of roll angle error

5 结 论

本文提出了一种基于SR-CH∞KF算法的高旋飞行器姿态测量方法。该方法将H∞滤波与SR-CKF算法相结合,提出了适用于线性-非线性系统的详细滤波算法。与众不同的是,该算法能够适用于量侧噪声不确定的情况下,利用更新新息序列来不断计算误差限定参数并不断修正量测噪声,可以有效降低量测噪声对实验结果的影响和提高测量系统的鲁棒性和滤波效率。通过仿真实验表明,SR-CH∞KF算法相比较于CKF和SR-CKF,可以有效地提高高旋飞行器的姿态解算精度,为后续飞行导航和控制奠定了良好的技术基础。