基于LASSA算法的多无人机协同航迹规划方法
2022-02-16汤安迪徐登武
韩 统, 汤安迪, 周 欢, 徐登武, 谢 磊
(1. 空军工程大学航空工程学院, 陕西 西安 710038;2. 空军工程大学研究生院, 陕西 西安 710043; 3. 中国人民解放军94855部队, 浙江 衢州 324000)
0 引 言
随着无人机(unmanned aerial vehicle, UAV)技术的不断发展,其在执行情报侦察、作战打击等行动中的作用得到不断显现。UAV航迹规划是UAV执行作战任务不可缺少的一个环节,是指在综合考虑UAV自身性能、环境因素和任务要求的情况下,找到一条或多条满足一系列约束的从起始位置到达目标位置的可行的、最优或近似最优的飞行航迹。UAV航迹规划问题是一个典型的非确定性多项式问题,随着规划空间增大、约束增多,计算量迅速增长,对于算法的性能要求也越来越高。
目前,常用的UAV航迹规划算法分为两类:一类是传统的优化算法,包括A算法、Dijkstra算法、人工势场法和快速搜索随机树(rapidly exploring random trees,RRT)。另一类则是智能优化算法,如:遗传算法(genetic algorithm, GA)、差分进化(differential evolution, DE)算法、人工蜂群(artificial bee colony, ABC)算法、蚁狮优化(ant lion optimizier, ALO)算法、灰狼优化(grey wolf optimizer, GWO)算法等。由于维度不断增加,求解难度呈指数式增长,传统的优化算法难以保证优化的效果。而智能优化算法具有结构简单、寻优精度高、收敛速度快、鲁棒性较强等特点,已被广泛应用于航迹规划问题求解。
随着军事作战任务复杂性的不断提高,单UAV作战已经不能满足需求,多UAV协同作战逐渐成为发展趋势,而多UAV协同航迹规划相比单机航迹规划,约束增多,计算量进一步增加。文献[22]将Hooke-Jeeves搜索算法引入到粒子群算法中,改善粒子的局部搜索能力并将改进后的粒子群算法应用到多UAV协同航迹规划问题求解。文献[23]提出基于使用不同的变异策略的改进DE算法的多UAV航迹规划。文献[24]将人工蜂群算法和模拟退火算法相结合,并求解二维协同航迹规划问题。以上研究虽然实现了多UAV协同航迹规划,但它们在规划航迹质量、寻优求解效率等方面仍有进一步改进空间。
麻雀搜索算法(sparrow search algorithm,SSA)是薛建凯于2020年提出的一种基于种群的元启发式优化算法。SSA通过模拟自然界中麻雀种群的捕食和躲避机制来建立优化模型,具有问题求解适应性强、模型参数简单易懂、寻优性能较强等特点,已被用于求解单无人机航迹规划问题。但和其他群智能算法一样,在求解复杂工程优化问题时,存在迭代后期种群多样性降低,易于陷入局部最优的缺陷。针对SSA存在的不足,本文使用对数螺旋策略和自适应步长策略来改进,并将其应用于多UAV协同航迹规划问题求解。首先对数螺旋搜索策略和SSA发现者的原始搜索策略相结合,增大算法的搜索空间,增强种群个体多样性,同时使用自适应步长策略,更好的控制算法的开发和探索行为,最后利用贪婪策略保留优势个体,保证算法收敛效率。将SSA、文献[26]中的混沌SSA(chavs SSA, CSSA)和本文提出的使用对数螺旋策略和自适应步长策略的SSA(logarithmic spiral strategy and adaptive step size strategy of the SSA,LASSA)在无威胁环境和有威胁环境下分别进行仿真实验,实验结果验证了协同航迹规划模型的有效性和LASSA的优越性。
1 UAV航迹规划建模
1.1 战场环境构建
战场环境构建问题,主要是解决三维地形环境的建立以及各类威胁的建立。
本文使用数字高程地图(digital elevation map, DEM),建立的三维山地地形描述如下:
={(,,)|0≤≤,0≤≤,0≤≤}
式中:,,分别表示在战场环境中的任意一点的横坐标、纵坐标以及高度;,,为战场环境的边界值。
由于本文主要考虑静态航迹规划,在执行任务前会通过各种探测手段获得敌方防空系统的部署方位和相应武器性能。此外,UAV主要依靠低空突防实施打击任务,在遭遇敌方雷达或防空火力时,通常采用贴近地面转弯进行规避,而非爬升高度摆脱。
基于上述考虑,为了保证UAV在执行作战任务过程中的生存几率及航迹规划模型的简洁性,本文将威胁源的威胁范围等效为最大横截面积覆盖威胁区域的圆柱体障碍模型。综上,战场环境构建如图1所示。
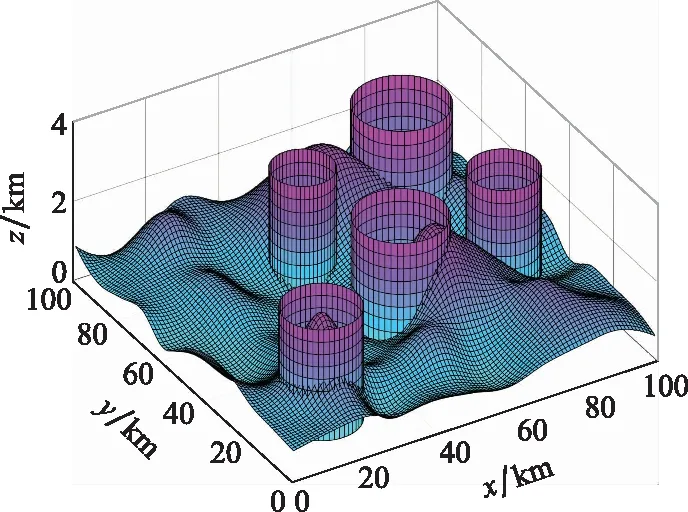
图1 地形威胁示意图Fig.1 Topographic threat map
1.2 单UAV航迹规划约束条件及目标函数
求解航迹规划问题需要建立合适的适应度函数以及考虑影响航迹质量的各类约束。静态全局三维航迹规划模型主要包含两个方面,一是代价函数,也就是智能优化算法的目标函数,我们需要考虑UAV的飞行油耗代价、飞行高度代价以及综合威胁代价;二是UAV本身性能约束,如最大飞行航迹约束、最低飞行高度约束、最大转弯角约束和最大爬升角约束。
1.2.1 飞行油耗代价
在实际作战任务中,UAV携带的燃料是有限制的,UAV不可能无限制地飞行,需要保证UAV在执行完任务之后安全返回。在本文中,假定UAV执行匀速率飞行,因此航迹长度的大小反映了燃油消耗大小,即UAV飞行油耗代价可用航迹长度表示:
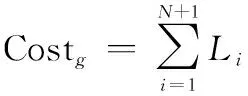
(1)
式中:是第段航迹长度。
1.2.2 飞行高度代价
低空飞行有利于发挥地形屏蔽的作用,减少被雷达探测的风险。所以要求UAV在执行任务过程中尽可能以低的高度飞行,则飞行高度代价可表示为
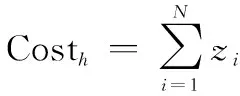
(2)
式中:为第个航迹点对应高度。
1.2.3 威胁代价
UAV在执行对地攻击任务时会遭遇敌方的防空系统,其中包括探测雷达、防空高炮、地空导弹等威胁,将上述威胁在三维平面上近似看作一个个圆柱体区域,探测范围或打击范围作为其半径,规定UAV不能通过圆柱体区域,当航迹点或航迹段在圆柱体区域内,即认为该航迹不可行。
1.2.4 最大飞行航迹约束
为确保UAV在执行完作战任务后,能够有足够燃油返回基地,假定UAV所携带燃油能飞行的最大航程为,则最大飞行航迹约束为
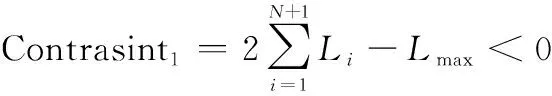
(3)
1.2.5 飞行高度约束
在UAV执行低空突防打击任务时,虽然贴地飞行能够降低被雷达探测的概率,但在实际作战空间中,由于地形复杂,容易发生飞机坠地的风险,因此为了保证UAV飞行安全,需要设定一个最低飞行高度,那么UAV飞过的每段飞行航迹高度应满足如下约束:
Constraint=-<0
(4)
1.2.6 最大转弯角约束
UAV在实际飞行过程中,由于其本身机动性能的限制,需要将转弯角设定在一个安全数值范围内;同时在转弯过程中,为了保证UAV能够有效按照规划出的航迹进行飞行,所以要求生成的相邻航迹段间的夹角, 不能超过最大转弯角,需满足如下约束:
Constraint=max|, |-≤0
(5)
1.2.7 最大爬升角约束
最大爬升角是指UAV在飞行时可以爬升或下降的最大角度,是除最大转弯角外另一个实现UAV机动的重要指标。同最大转弯角类似,UAV各航迹段之间的爬升角, 不能超过最大爬升角,需满足如下约束:
Constraint=max|, |-≤0
(6)
综上所述,本文所用的航迹规划目标函数为
min=·Cost+·Cost+·Penalty
(7)
式中:和分别为飞行油耗代价和飞行高度代价的权重系数,且满足+=1;为罚函数因子,通过引入罚函数的方式,将多约束优化问题转化为非约束优化问题进行求解;Penatly可表示为
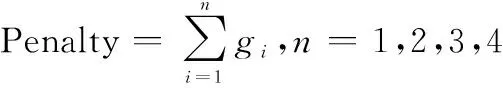
(8)

1.3 多UAV协同规划约束条件及目标函数
第1.2节对单机航迹规划模型进行了介绍,在本节中,将建立多机协同规划模型。在进行协同航迹规划时,需要提前在单机规划层为每架UAV规划出多条满足单机飞行约束的候选航迹,然后建立协同约束关系,对多个UAV进行协同航迹规划。协同约束主要包括多UAV之间的空间协同约束和时间协同约束。空间协同约束是指在满足单UAV航迹规划的同时避免多架UAV之间发生碰撞。时间协同约束是指多架UAV能够在同一时刻或在一定的时间差内到达指定目标点。由于本文研究静态三维航迹规划,未对实际飞行速度进行规划,因此在实际飞行过程可以通过调节每一时刻的飞行速度来避免空间上的碰撞。所以本文主要考虑时间协同约束。多机协同航迹规划层的具体操作为:首先生成每架UAV的多条候选航迹,然后根据每架UAV的速度和航迹长度,计算其到达目标点的时间范围并求不同UAV之间到达目标区域的时间交集,接着确定协同时间范围,最后选择满足约束的最小协同代价对应的飞行方案。
1.3.1 时间协同约束
当多UAV协同执行任务时,若无法同时到达任务目标区域,不仅会降低UAV的协同工作效率,还会增加单架UAV被击毁的概率,导致任务完成率降低,因此需要对UAV到达目标区域的时间进行约束,也就是设定协同时间,即满足所有UAV到达目标区域的时间区间的交集,当交集不为空时,表明存在一段时间区间使UAV能够通过调节飞行速度同时到达目标点。
如图2所示,以3架UAV为例,其中两条红线之间的部分,即是各架UAV能够同时到达目标点的时间交集。设第架UAV的第条飞行航迹为, ,每架UAV的速度∈[,],则第架UAV按照第条飞行航迹到达目标点的飞行时间范围, =[, ,, ],那么第架UAV总的时间范围则为=,1∪,2∪…∪,,那么时间协同约束为
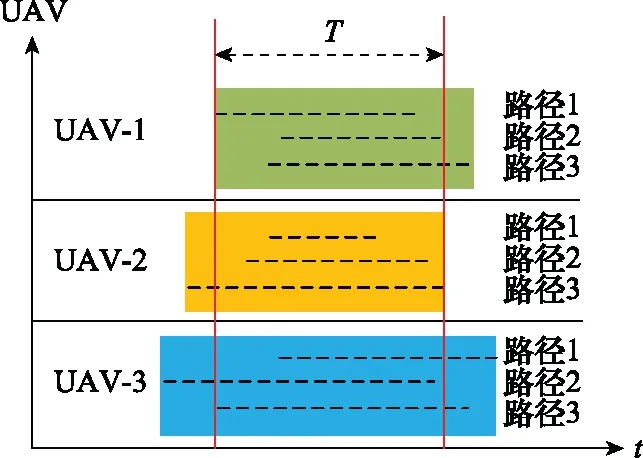
图2 协调预计到达时间机制Fig.2 Mechanism of coordinated estimated time of arrival
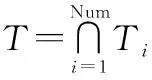
(9)
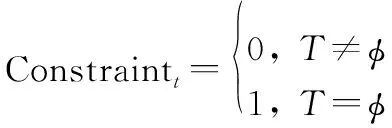
(10)
式中:Num为UAV架数。
1.3.2 协同目标函数
协同目标函数包括两部分,一部分是各架UAV从备选航迹组中选出的一条飞行航迹的航迹代价, ,另一部分则是规划出的协同时间代价,为了最小化UAV的协同代价,取协同时间交集中的最小值min()为。因此,协同目标函数为
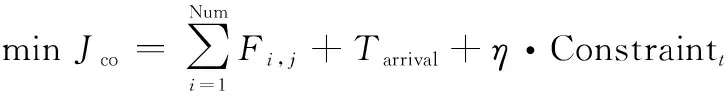
(11)
式中:, 为第架UAV选择的第条飞行航迹的航迹代价。
2 螺旋自适应SSA
2.1 基本SSA
SSA是一种基于种群的元启发式优化算法。SSA主要通过模拟麻雀种群觅食行为来建立优化模型进行寻优。在SSA中,以最小值问题为例,适应度值较小的麻雀个体被视作发现者,其他个体则作为跟随者,同时在整个麻雀种群中随机选取一定比例的个体作为警戒者,当侦察到危险时则改变它们的位置。
SSA将整个种群划分为发现者、跟随者以及警戒者。它们分别按照各自规则进行位置更新,具体数学模型如下所示:
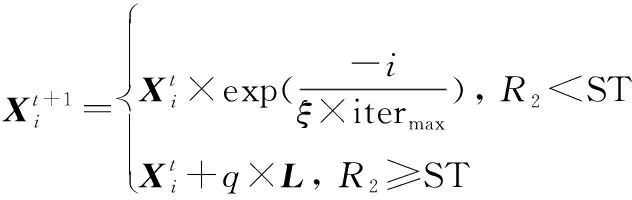
(12)
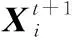
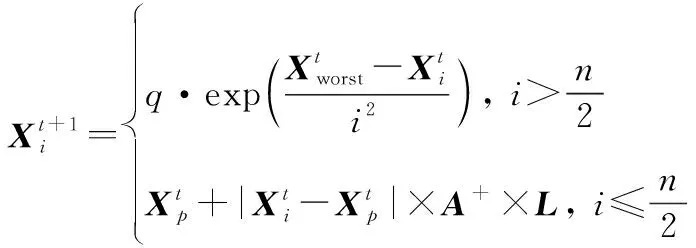
(13)
式中:表示被发现者占据的最佳位置;表示当前最差位置;是一个由1和-1组成的向量。
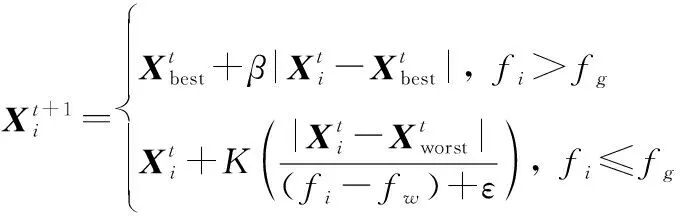
(14)
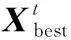
2.2 螺旋自适应SSA
为了改善SSA算法性能,进一步提高SSA的收敛速度和局部最优规避能力,本文针对SSA在迭代寻优过程中,种群发现者的更新主要朝着个体最优解直线靠近,导致算法迭代后期种群个体多样性迅速降低,易于陷入局部最优的不足,首先将对数螺旋策略与原始搜索策略相结合,扩大对个体周围的搜索,平衡发现者的开发与探索能力,其次使用两种自适应步长策略更新警戒者位置,更好地控制算法的开发和探索行为,最后使用贪婪策略保留子代和父代中优秀个体,保证收敛效率。
2.2.1 对数螺旋策略
测序后的片段在NCBI中进行Blastx比对,选取与其同源的代表性氨基酸序列用ClustalX(version 1.83)进行多序列比对,用 MEGA 5.05 软件中的最大似然法构建系统进化树,选用Jone-Taylor-Thomton(JTT)模型,进化树用自展分析法进行检验,循环1 000次。
通过实验发现,原始SSA算法易于陷入局部最优,从而导致过早收敛,对于原始SSA算法,如图3(a)所示。
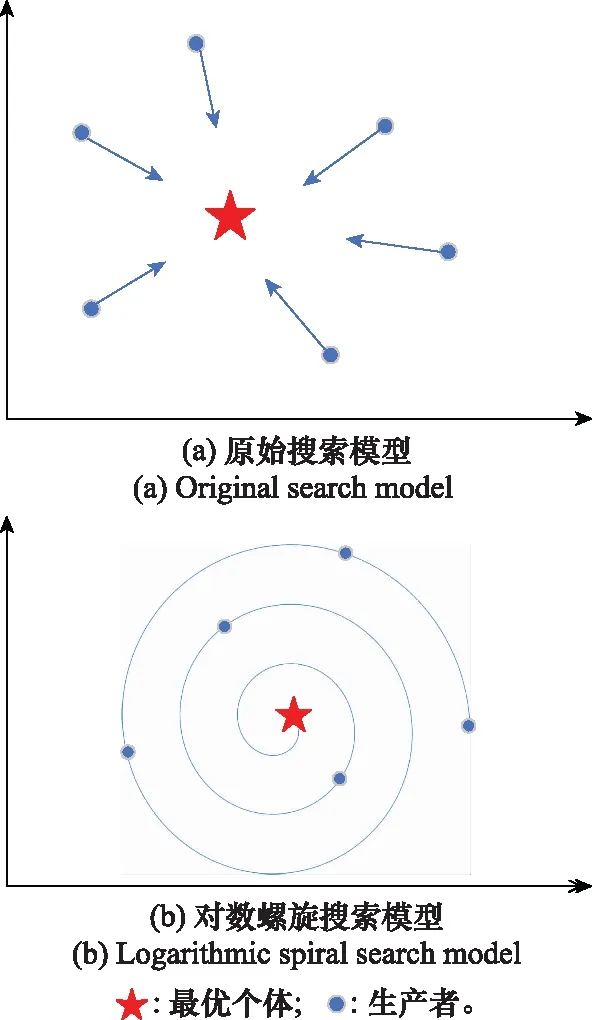
图3 两种搜索模型的说明Fig.3 Illustration of two search models
其发现者的每次迭代更新朝着个体最优解直线靠近,这样有很强的开发能力,但是丧失了在靠近最优个体过程中对附近搜索空间的探索,种群多样性降低,容易陷入局部最优,因此我们引入一种对数螺旋搜索模型来解决这个问题,数学模型描述如下:
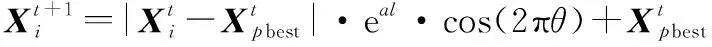
(15)
=2(1-iter)-1
(16)
式中:是一个决定螺旋形状的常数,取值为1;是一个从1线性递减至-1的参数;best为当前迭代个体的最优位置。从图3(b)可以得知,每代个体在更新位置时,以螺旋状逐步靠近,增加了对周围空间的搜索,使种群多样性得到维持,增强了算法的探索能力,基于此分析,我们将发现者位置更新公式调整如下:
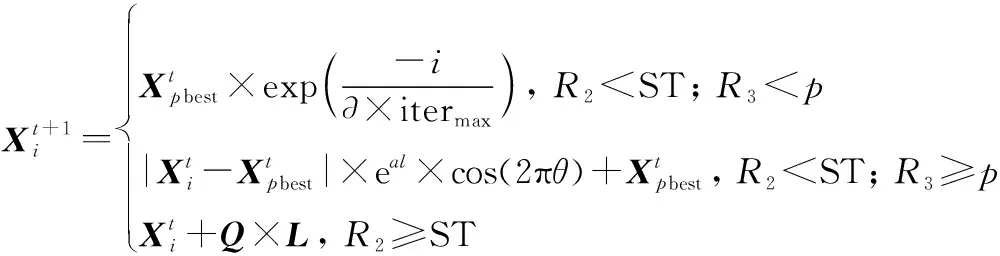
(17)
式中:为一个0到1均匀分布的随机数;为一个常数,取值为05。
2.2.2 自适应步长策略
在原始SSA中,对于警戒者位置更新采用两种策略,对适应值较差个体使用高斯分布产生步长,由图4可以得知,高斯分布产生较小步长的概率较高,这不利于算法的全局搜索。对于适应值较好的个体采用随机步长策略,在迭代后期仍有较大概率产生大步长,不利于算法收敛。基于上述分析,为了平衡算法的开发和探索能力,增强算法收敛速度,分别针对两种策略提出自适应步长更新公式:
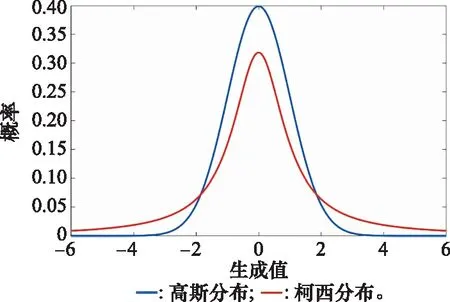
图4 高斯-柯西分布密度函数Fig.4 Gauss-Cauchy distribution density function

(18)
=(2rand-1)·(1-/iter)
(19)
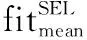
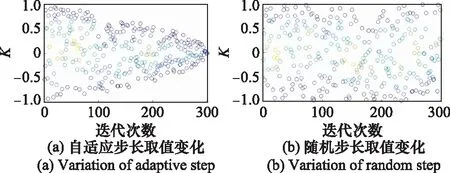
图5 新旧步长比较Fig.5 Comparison of new and old step strategies
2.2.3 算法复杂度分析
时间复杂度是衡量算法寻优速度的一个重要指标,在这一部分对本文提出的改进SSA进行时间复杂度分析。
设种群规模为NP,每只麻雀个体维度为,初始化麻雀种群参数的时间为,在每一维度上随机生成均匀分布的随机数的时间为,求解测试函数的时间为()。初始阶段的时间复杂度为
=(+NP(+()))
(20)
对于改进算法,对数螺旋策略和原始策略随机选择,假设发现者数量为·NP,为发现者占种群的比例,对数螺旋策略的时间为,原始策略的时间为,因此发现者时间复杂度为
=(·NP·(+))
(21)
跟随者数量为(1-)NP,假设每一维更新时间为,那么跟随者阶段时间复杂度为
=((1-)NP·)
(22)
警戒者数量为·NP,为警戒者比例,假设每一维更新时间为,那么警戒者阶段的时间复杂度为
=(·NP·)
(23)
综上,改进SSA的时间复杂度为
=+(++)=(+())
(24)
2.3 航迹规划方法框架
综上所述,基于螺旋自适应SSA的多UAV协同航迹规划方法框架如图6所示。
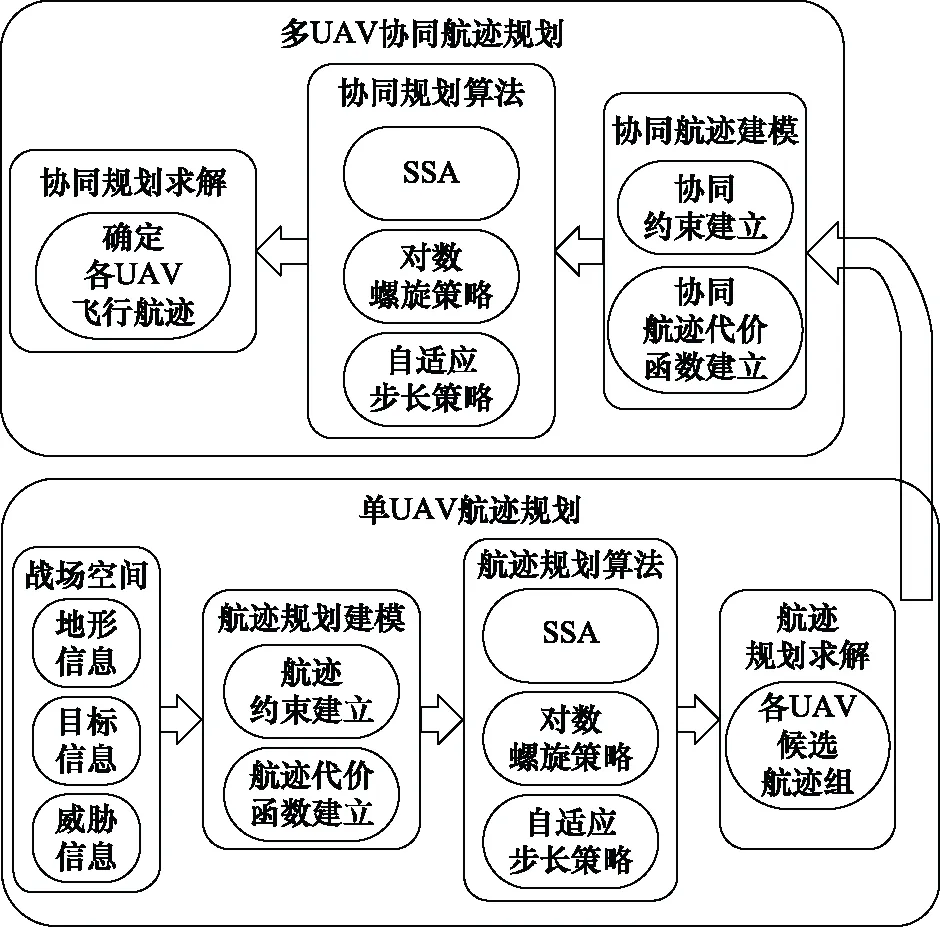
图6 多UAV协同航迹规划方法框架Fig.6 Framework of multi-UAV cooperative path planning method
3 仿真实验与分析
为了验证本文提出的基于LASSA的多UAV协同航迹规划方法的有效性,在AMD R7 4 700U,1.8 GHz,16 GB RAM的仿真平台上进行实验,编程环境为Matlab R2016b。仿真实验参数设置如下所示:战场空间为=100 km,=100 km,航迹节点数Dim=20,最大转弯角为60°,最大爬升角为60°,最大航程为550 km。飞行油耗代价=065,飞行高度代价=035,罚函数因子=10。种群数为50,最大迭代次数为300。实验分为两组共3种情况。第1组为单UAV航迹规划仿真实验,使用SSA、CSSA和LASSA分别进行规划,验证本文提出改进算法的性能。第2组分两种情况,分别为无危胁下的协同航迹规划和有威胁下的协同航迹规划,用于验证本文提出的协同航迹规划模型的有效性。
3.1 单UAV航迹规划仿真实验
UAV起点为(3 km,6 km),目标点为(96 km,94 km),威胁源参数如表1所示。3种算法分别独立求解单UAV航迹规划模型20次,统计结果记录在表2。
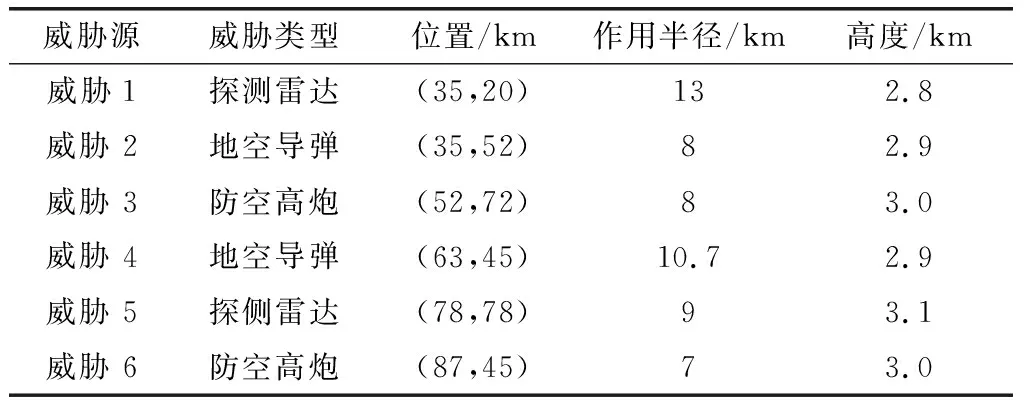
表1 威胁源参数
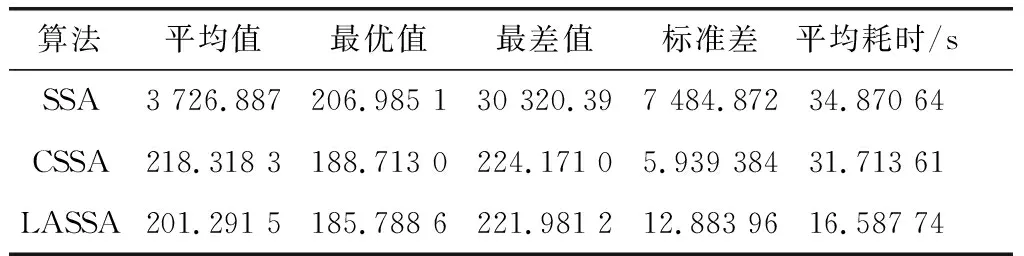
表2 单机航迹规划结果比较
从表2的统计结果来看,LASSA无论是在平均值、最优值还是最差值上,都是优于SSA和CSSA的,并且LASSA的平均耗时远远小于对比算法,这说明了本文提出的LASSA获得的航迹结果整体较优,且实时性更好,表明了本文提出的LASSA在寻优精度、算法鲁棒性和计算速度上有较大提升。图7(a)为各算法最优三维航迹图,图7(b)为在二维等高线地形图中的最优航迹。分析图7可以得知,SSA规划航迹虽能规避威胁,但其没有有效贴地飞行,在飞至(60 km,80 km)处,向上爬升,增加了UAV被敌方雷达探测的风险。而CSSA和LASSA在避免威胁的同时,能够尽可能沿地势较低地形飞行,有利于利用地形遮蔽,降低被敌方雷达探测到的几率。从图7可以得知,CSSA和LASSA在最优航迹上相差不大,但LASSA规划航迹更显平滑,没有过多的大幅调整航向。综上所述,本文提出的LASSA能够更快速地、更稳定地获得满足约束的飞行航迹。
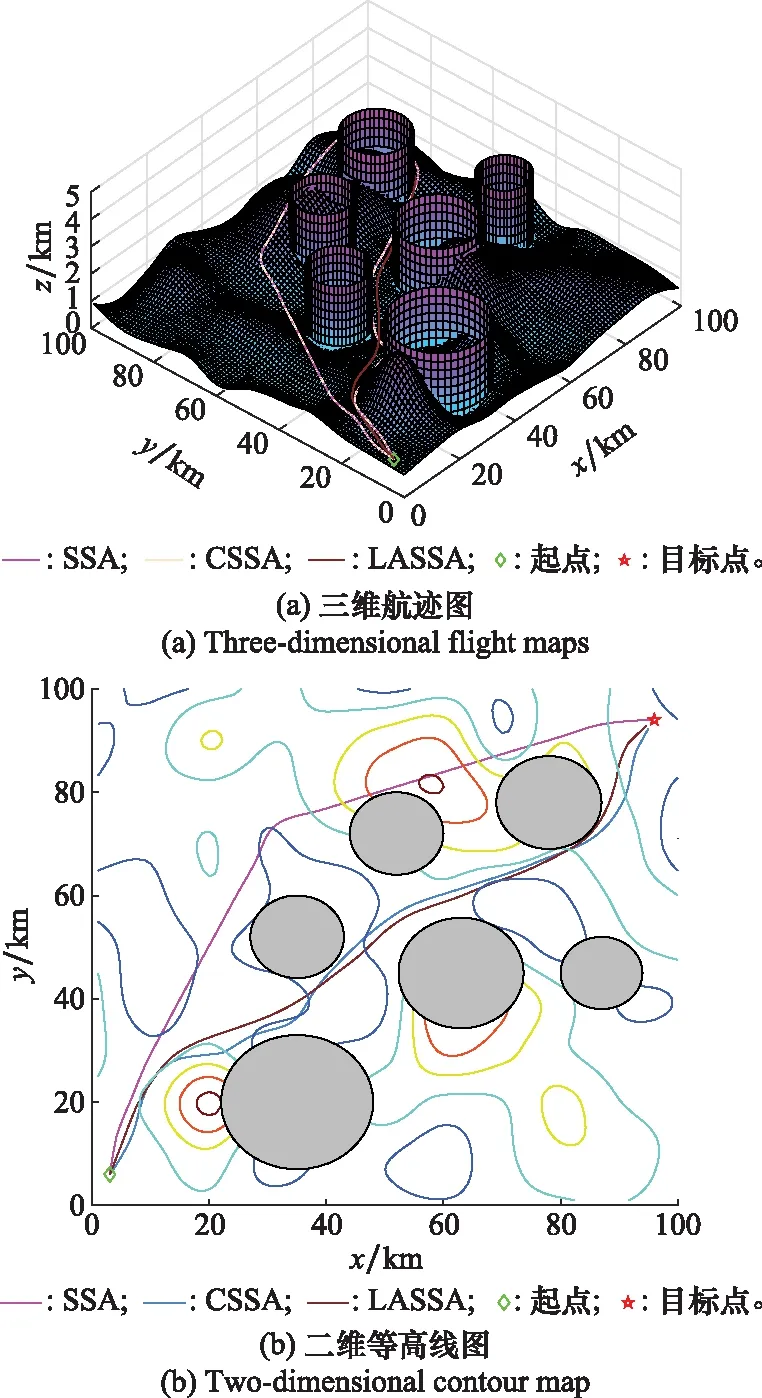
图7 单UAV航迹规划结果Fig.7 Single UAV path planning results
3.2 多UAV协同航迹规划仿真实验(无威胁)
为验证多UAV协同航迹规划方法的有效性,首先进行无威胁下的仿真实验,3架UAV起点分别为UAV-1(10 km,15 km),UAV-2(3 km,10 km)和UAV-3(7 km,4 km),终点分别为(95 km,75 km),(90 km,80 km)和(95 km,70 km),备选航迹数为20,=0.7 Ma,=0.4 Ma。各UAV分别规划的备选航迹组结果如表3所示,协同航迹规划结果如表4所示。
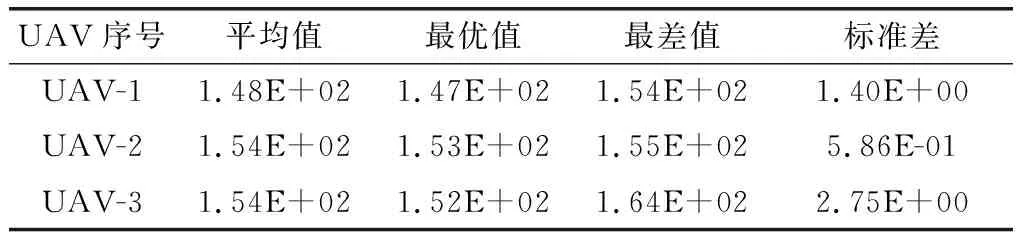
表3 航迹规划层结果(无威胁)
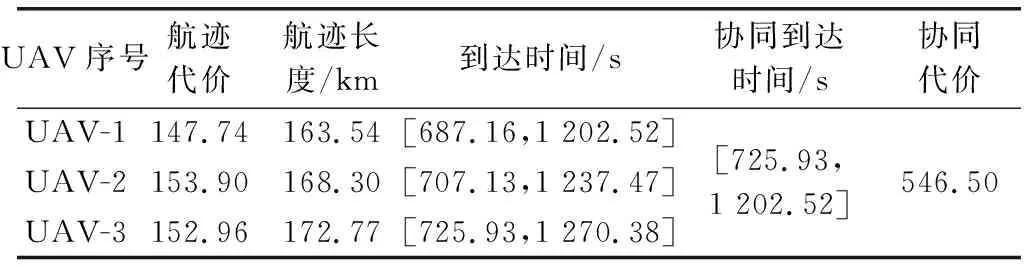
表4 协同规划层结果(无威胁)
由表3可以得知,在无威胁条件下,LASSA能够较为稳定地为各UAV规划出满足约束的备选航迹组,进一步验证了本文提出LASSA的稳定性。表4表明各UAV可以在[725.93,1 202.52]区间内协同到达目标点,而在同时起飞725.93 s后到达目标点的情况下,协同代价为546.50。另一方面,3架UAV所选航迹并非都是最优的,这也说明协同航迹规划的结果并不一定使各UAV都能按照最优航迹执行任务,而是在满足协同要求的情况下,选择相对更好的航迹执行任务。从图8可以得知,各UAV飞行航迹能够避开较高地势,遇到山峰时,能够转弯绕行,从而实现紧贴地形飞行的目的。
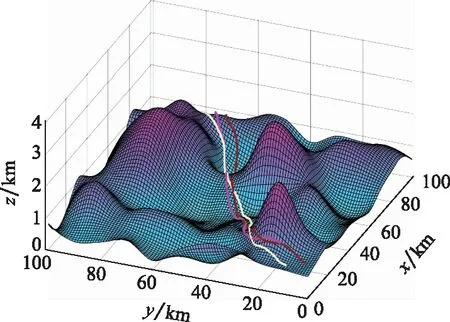
图8 协同航迹规划结果(无威胁)Fig.8 Cooperative path planning results (no threats)
接下来进行威胁条件下多UAV协同航迹规划仿真,采用表1威胁源参数,其余实验条件与第4.2节无威胁条件协同航迹规划仿真相同,独立运行20次,统计航迹规划层结果和协同规划层结果于表5和表6。
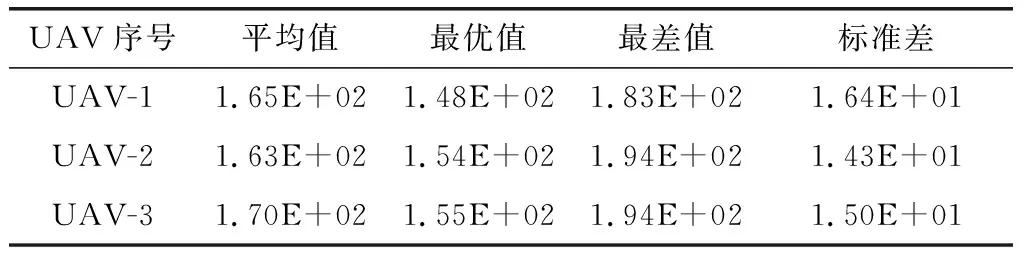
表5 航迹规划层结果(威胁)
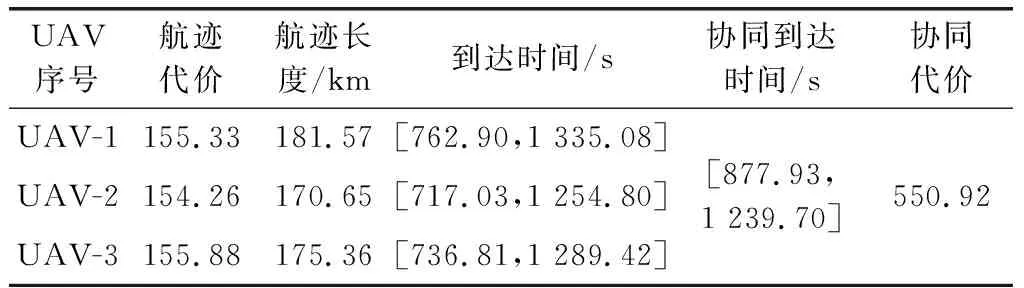
表6 协同规划层结果(威胁)
由表5可知,LASSA为各UAV规划的航迹组皆满足单机航迹规划约束,进一步说明了该算法在求解复杂约束优化问题时的良好性能。表6则是在威胁条件下的协同航迹规划结果。相较于无威胁条件,威胁条件下选择的航迹长度皆有增加,这也导致了最小协同到达时间和协同代价的增大。图9(a)和图9(b)展示了协同代价为550.92下的航迹规划结果。
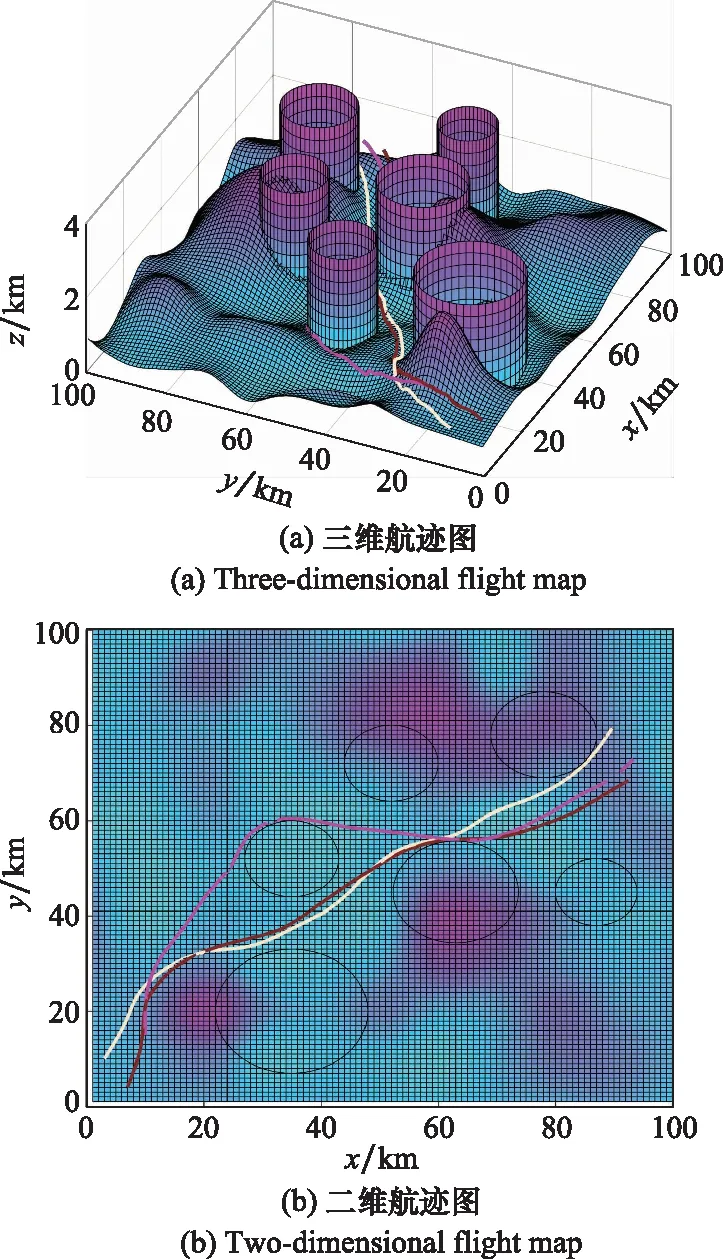
图9 协同航迹规划结果(威胁)Fig.9 Cooperative path planning results (threats)
图10和图11分别为各UAV飞行过程中转弯角和爬升角的变化情况,分析可知,3架UAV在执行任务时,无论是爬升角还是转弯角,其变化量都稳定在一个较小的区间范围内,远远小于60°的最大值限制,说明LASSA规划的航迹质量较高。图12为协同代价收敛曲线,由图可知,算法能够很快收敛至全局最优解,验证了本文提出协同航迹规划模型的可行性和改进算法的优越性。
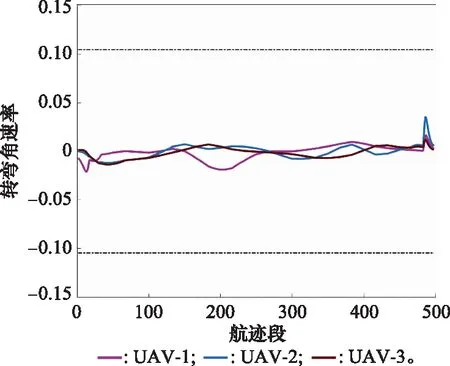
图10 转弯角变化情况Fig.10 Turning angle variation
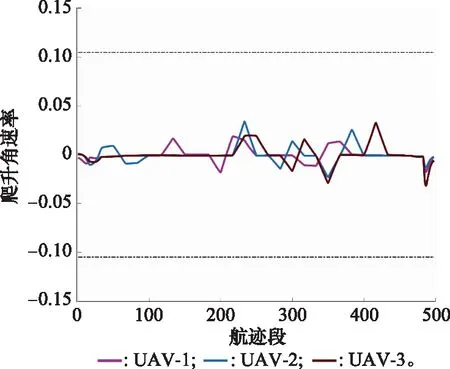
图11 爬升角变化情况Fig.11 Pitch angle variation
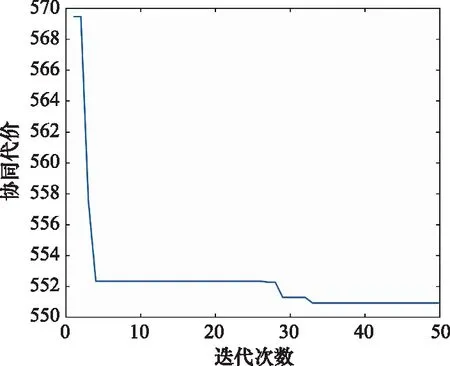
图12 协同代价的收敛曲线Fig.12 Convergence curve for cooperative cost
4 结 论
本文针对无人机航迹规划问题,利用分层规划思想建立单UAV航迹规划模型和多UAV协同航迹规划模型。
为克服基本SSA在迭代后期种群多样性降低,易于陷入局部最优的缺陷,本文将对数螺旋策略和发现者搜索策略结合,扩大搜索范围,增强算法的种群多样性;引入两种自适应步长策略,更好地调节算法的开发和探索能力;并使用贪婪策略保证算法的收敛速度。
单UAV航迹规划结果表明LASSA性能优于SSA和CSSA;两种多UAV协同航迹规划仿真实验则进一步验证了本文提出的算法具有更好的收敛精度,更快的计算速度,同时证明了本文所提出的多UAV协同航迹规划模型的可行性。
