基于Stacking集成元模型的作战体系能力图谱生成方法

马 骏, 杨镜宇, 邹立岩1,

(1. 国防大学研究生院, 北京 100091; 2. 国防大学联合作战学院, 北京100091)

0 引 言

作战体系能力图谱是在作战仿真实验的基础上,利用可视化技术对作战体系某种能力的直观表达,是从整体分析作战体系能力的有效方法。然而,作战体系能力图谱的生成,通常需要对海量实验方案空间进行仿真,以生成不同约束条件下的仿真实验结果。同时,作战仿真系统已发展为模型逐渐完善、结构日益复杂、行为不断演化的复杂系统。在此基础上,对大样本空间进行探索,需要耗费巨大的计算资源,对某一问题的仿真实验往往需要历时数天甚至数周。特别是在需要“即时”得到实验结果的紧迫形势下,利用复杂的作战仿真系统进行作战实验更是难以达到需求。

元模型也称代理模型,即“模型的模型”,是复杂物理模型的简化模型。通过建立元模型的方法,可以在保证实验精度的前提下,大量减少实验开销。本文所述的元模型是仿真元模型,通过获取作战仿真系统的输入输出,建立逼近仿真系统输入输出关系的映射函数,并以此代替复杂的作战仿真系统进行实验分析和探索。

元模型广泛应用于产品设计、工业控制、风险分析等诸多领域。在军事方面,文献[3]为评估战斗系统性能,建立了战术仿真模型的元模型;文献[4]通过建立神经网络元模型,替代了部分仿真模型,并分析了元模型在军用仿真中的作用;文献[5]使用神经网络元模型，提高了复杂系统仿真效率;文献[6]使用元模型对海军水雷探测模型进行了验证;文献[7]建立了装备费用评估元模型;文献[8]在美空军建模技术研究中,提出了综合运用元建模和因果推理技术的主动元建模,用现象学知识改进元模型质量,开启了主动元模型研究的新领域。在国内,文献[9]提出了元模型多拟合方法和两类组合元模型,并应用于雷达探测与跟踪;文献[10]建立了支持向量机主动元模型,并应用于导弹攻防对抗;文献[11]面向作战实验分析,提出了智能集成的元建模方法。仿真元模型技术的发展为提高复杂仿真系统效率、快速准确生成作战体系能力图谱提供了有效途径。

1 问题分析

1.1 相关概念

1.1.1 作战体系能力图谱

作战体系能力图谱,是通过可视化表现体系能力的方法。美军认为,能力是在特定的标准和条件下,通过各种方法和手段完成一组任务后，达到期望效果的本领;效能是在一定条件下,实现预定功能、达成预定目标的程度。相比较而言,能力是对完成任务内在条件的度量,效能是对完成任务效果的度量。对于作战体系而言,其能力是体系固有的属性,以体系能力作为研究对象和目标,更能反应作战体系的整体性特点。在作战体系的层面,能力和效能往往是不可分割的,能力评价的基础是效能,能力通常难以用某些系统的量化的指标来表达,需要用体系效能对体系能力进行描述。

由于作战体系具有整体、动态、对抗等特性,作战体系的能力也随作战任务、环境、对手的变化而表现出不确定性,这使得在原理上无法用定量的方式准确的描述其能力。体系能力图谱的方法是基于探索性仿真的思想和数据耕耘的框架,针对体系的某种能力,通过多维度、大样本采样和仿真实验,获取不同环境下体系效能的多种度量,并综合可视化分析技术,以获得体系该能力的全貌。

1.1.2 元模型

文献[15]讨论了元模型、仿真模型与真实系统三者之间的关系,如图1所示。

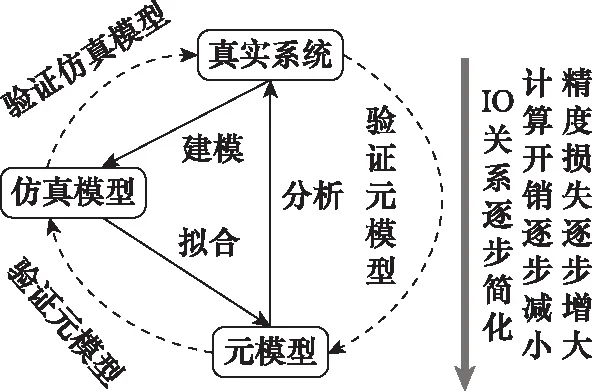
图1 元模型、仿真模型及真实系统之间关系Fig.1 Relationship among meta-model, simulation model and real system

真实系统经过建模生成仿真模型,使用仿真模型的输入输出信息拟合产生元模型,然后应用元模型对真实系统进行分析。模型验证时,通过真实系统对仿真模型进行检验,通过仿真模型或真实系统对元模型进行检验。

从真实系统到仿真模型再到元模型的过程中,真实系统的输入输出关系得以逐步简化、计算开销逐步减小,但是也造成了对真实系统求解的精度损失逐步增大。因此,在应用元模型时,应充分考虑计算开销与精度之间的均衡关系。

元模型的构建过程可以表示为以下四元组:

Metamodel=(,,,)

(1)

式中：为实验设计的方法集合;为仿真实验的数据集合;为元模型类型和结构的集合;为元模型评估方法及标准的结合。

基于上述描述,元建模(meta-modeling)的基本过程可概括为:

选定∈,运用该实验设计方法,选择实验点并运行仿真模型,得到仿真实验结果数据;

将数据集划分为训练数据集和测试数据集;

选定∈,运用该元模型类型和结构,对进行拟合,得到元模型meta-model;

利用中的评估方法和标准,以及测试数据集,对meta-model进行检验。

1.1.3 集成学习

集成学习是机器学习的重要分支,通过构建并结合多个学习器来完成学习任务。通常,一个集成学习器由多个基学习器组成,每个基学习器可以对数据集从不同角度进行描述,形成互补。因此,集成多个学习器的建模方法可以有效提升模型的有效性、泛化性和可信度。

一般情况下,集成学习的构建需要两个步骤:一是训练基学习器。为取得较好的集成效果,通常需要基学习器尽可能达到准确性和多样性两个标准；二是将基学习器按照一定方法结合起来。

常用的集成策略包括:均值法、投票法和学习法。但是,当集成规模较大时,加权、平均等方法易造成过拟合。学习法的基本思想是,以若干基学习器为一级学习器,将其输出作为二级学习器的输入特征,以原始样本的标记为新的标记,以此新数据集训练二级学习器。通常,按照集成学习的结构,可以将集成学习算法分为Boosting方法、Bagging方法、Stacking方法。

Stacking是学习集成法的典型代表,该方法通过训练二级学习器来结合若干一级基学习器。Stacking可以看作是一种通用的集成框架,其结构与Bagging相似,是一种并行集成的方法,与Bagging不同的是,其一级基学习器通常使用异质学习器,集成策略使用学习法,即构建二级学习器,如图2所示。

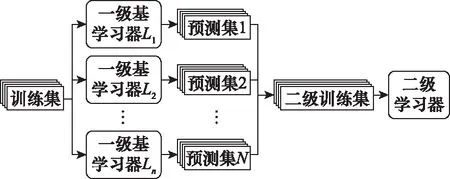
图2 Stacking集成算法流程图Fig.2 Stacking integrated algorithm flow chart

1.2 作战体系能力图谱生成方法

传统的仿真实验方法,通常难以处理作战体系不断演化的问题,不能有效聚焦到影响体系能力的关键因素。作战体系能力图谱的生成方法,在大规模探索性仿真实验的基础上,构建了一个多重迭代、逐步聚焦的实验框架,主要包括线索提炼、数据栽培、数据收获、综合分析等步骤。

其中,线索提炼步骤包括对实验问题的提炼、能力指标的选取、实验范围的剪裁、采样方法的选择等;数据栽培步骤主要包括模型开发、想定部署、仿真样本生成、仿真实验运行等,通过该步骤得到生成图谱所需的数据集;数据收获步骤针对研究问题对实验数据进行处理,通过选择合理的可视化方式,构建特定的能力图谱;综合分析步骤是根据生成的作战体系能力图谱,对作战体系进行整体分析,得出分析结论的过程。

基于元模型的作战体系能力图谱生成方法,是在数据栽培环节,采用构建元模型的方法,用元模型代替仿真模型,得到仿真实验数据,如图3所示。因此,构建合理的元模型是基于元模型生成作战体系能力图谱的研究重点。

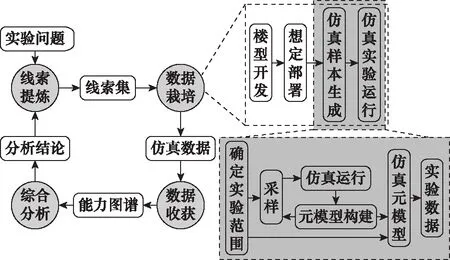
图3 作战体系能力图谱生成步骤Fig.3 Generation steps of operational system of systems capability graph

1.3 研究重点

使用元模型解决作战体系能力图谱的生成问题时,需要解决以下问题:一是需要元模型有较高的精度,能有效反应仿真模型的特征;二是需要元模型有较强的适应性,能够在不同应用条件下有较强的鲁棒性;三是需要元建模的过程有较高的效率,能快速对大量样本空间做出探索。本文从以下角度出发,解决上述问题:

一方面,通过Stacking集成学习的方法解决元模型的问题依赖性。Stacking集成元模型的构建思路是将集成学习的基学习器由若干“基元模型”代替,而后按照集成学习的方法和策略对基元模型进行结合,生成集成元模型。相比于其他方式,Stacking集成有以下优点:一是能有效集成多种异质元模型,提高模型整体的准确性和泛化性;二是该方式通过交叉验证的方法构造次级学习器的训练数据集,避免了直接使用原始数据训练可能造成的过拟合风险。

另一方面,通过序贯采样,平衡采样次数和模型精度,可以提高能力图谱生成效率。训练元模型样本的规模和质量,将直接影响建模的效率和精度。通常情况下,构建元模型只用一次采样,即一步法,然而,如果一次采样点较多,则需要多次运行仿真模型,降低构建集成元模型的效率;如果采样点较少,则会影响集成元模型的精度。通过序贯法逐步增加样本点,不断更新集成元模型,当集成元模型满足收敛条件时停止抽样,合理权衡模型精度与建模效率。

2 基于序贯采样策略的Stacking集成元模型

2.1 基本思路

本文提出的基于序贯采样策略的Stacking集成元模型构建方法如图4所示。

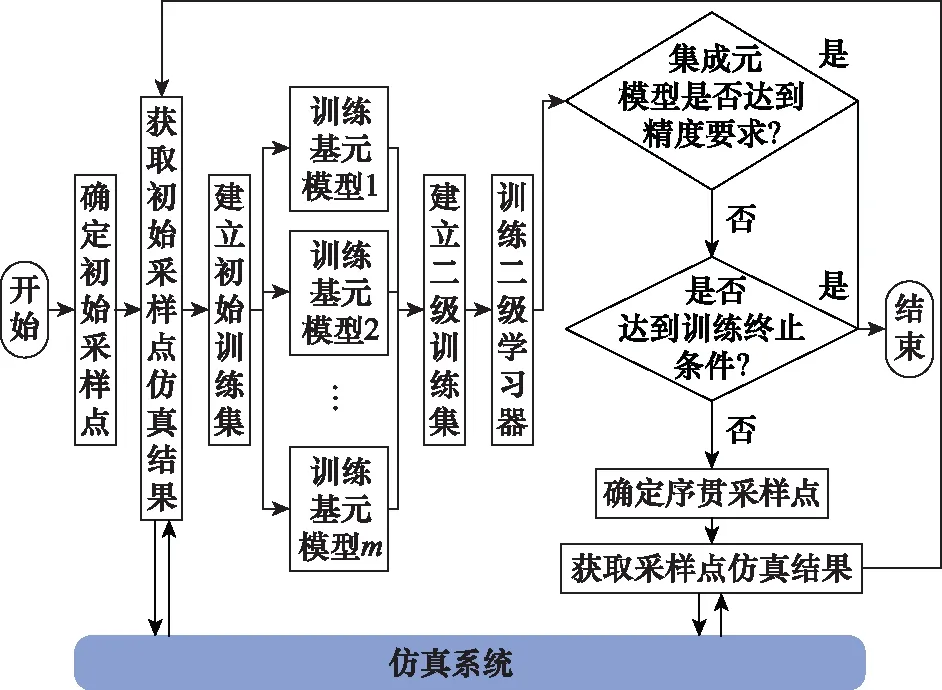
图4 基于序贯采样策略的Stacking集成元模型Fig.4 Stacking integrated meta-model based on sequential sampling strategy

根据体系能力图谱生成所需的实验范围,选择适当的实验设计方法,确定若干初始采样点={,,…,};

使用仿真系统,获取初始采样点对应的仿真运行结果={,,…,};

建立训练基元模型的初始数据集=∪={(,),(,)…(,)};

使用折交叉检验训练个基元模型;

将组预测结果与其对应的仿真结果合并生成二级模型数据集;

训练二级学习器;

用测试集对集成元模型的精确度进行测试,达到要求则结束训练,否则进入下一步;

判断是否达到训练次数或训练时间的上限,若达到上限则结束训练,否则进入下一步;

在初始采样点的基础上,运用序贯采样策略,确定新的采样点′;

2.2 两级模型的选择与构建

2.2.1 基元模型的选择与构建

选择与构建基元模型需要同时考虑各模型的准确性和多样性,本文通过集成多个异质元模型提升模型的多样性,主要使用多项式响应面(polynomial response surface,PRS)模型、Kriging模型、支持向量回归(support vector regression, SVR)模型、径向量(radial basis function, RBF)神经网络模型等元模型,在建立基元模型时,通过比较或优化算法等方式保证其准确性。

(1) PRS通过多项式的线性组合,拟合一个响应面,以模拟真实状态曲面。该模型有较好的透明性,在拟合中低维度、低非线性问题时具有一定优势。当数据维度较高,采用高阶多项式模型时,需要大量样本才能计算出所有未知系数。基于上述特征,本文采用探索式方法,分别建立不超过5阶的PRS模型,各阶模型中包含交叉项并通过折交叉验证建立,而后比较各阶PRS模型的指标,选取其中最高的作为组成集成元模型的PRS基元模型。

(2) Kriging是一种基于距离加权的差值近似法,适用于中低维度的高非线性问题,Kriging模型精度较高,可用少数样本数据逼近真实模型,对低维问题和高阶函数有较好的性能,但Kriging模型构造复杂,计算量较大。Jones等人对Kriging模型进行了深入的研究,提出了Kriging模型的全局最优化方法,通过给出的期望改善(expected improvement,EI)均衡全局和局部搜索能力,该方法目前在Kriging建模中应用较为广泛。本文使用基于上述算法的pyKiging工具包,以高斯函数为相关函数,通过粒子群优化(partical swarm optimization,PSO)算法对参数进行优化,建立Kriging基元模型。

(3) SVR是支持向量机(support vector machine,SVM)的一种实现方式,与传统回归模型相似,其基本思想是求解一个最优的超平面,使所有样本点到该超平面的误差最小。SVR模型在解决小样本高维问题时有一定优势。在构建SVR模型时,选择不同核函数会影响模型的精度,通常,选用核函数有两种方式:一是对数据集的特征有一定先验知识的情况下,基于先验知识选择核函数;二是通过试用不同的核函数,选择使用误差最小的核函数。在解决不同问题时,各数据集特征有较大差异,因此本文采用第二种方法,以线性核函数、多项式核函数、RBF核函数、Sigmoid核函数分别建立SVR模型,选择指标最好的核函数,建立SVR基元模型。

(4) RBF神经网络模型相比于使用核方法的SVR更适合大样本及高特征维度的数据情况。此外,文献[22]证明了相比于BP神经网络,RBF神经网络是连续函数的最佳逼近方式。在RBF神经网络中,常选择高斯径向基函数,建立RBF神经网络需要求解基函数中心点、方差、隐含层到输出层的权重等参数,常用的求解方法有3种:一是自组织选取中心的学习方法,该方法首先通过无监督学习求解中心点及方差,而后通过有监督学习求解隐含层到输出层的权重;二是直接计算法,通过随机在样本中选取中心点,计算相关参数,该方法通常用于数据分布有明显代表性的场景;三是有监督学习的方法,通过训练样本获取满足要求的网络参数,与BP神经网络学习原理相同,常采样梯度下降等方法修正误差。本文采取第3种方法建立RBF神经网络基元模型。

2.2.2 二级模型的选择与构建

二级学习器在很大程度上影响了Stacking集成学习的泛化能力,二级学习器的输入特征,即一级基元模型的输出特征,非常接近数据的真实标记,使用简单的模型作为二级学习器可以降低过拟合风险。

文献[23]建议使用线性回归作为二级学习器的算法。线性回归模型是最基础的回归模型,模型复杂度低,它通过连续的直线、平面或超平面拟合数据集,使得训练数据集的残差最小,能高效解决数据间有线性相关特征的问题。因此,本文选择线性回归模型建立二级学习器模型,对上述4个基元模型进行组合。

2.3 基于Stacking的基元模型集成

Stacking集成方法以两层结构在增强学习效果的同时确保模型不过于复杂冗余。本文基于Stacking的基元模型集成过程如图5所示,其整体过程可分为两步。

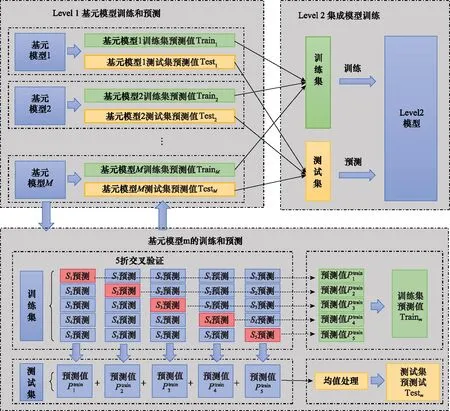
图5 基于Stacking的元模型集成Fig.5 Meta-model integration based on Stacking

训练第1层共个基元模型,利用各基元模型生成组训练集预测值和测试集预测值。该步骤中,对每个基元模型的训练和预测都基于折交叉验证的思想,Stacking方法常用=5,该步骤具体过程如下:

取基元模型∈,执行以下步骤;

将训练集划分为份,记为,,…,,

使用至训练基元模型;

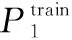
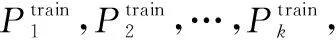
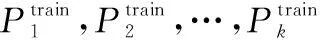
重复步骤1.1～步骤1.6,遍历所有个基元模型。

训练第2层集成模型。

根据步骤1中个基元模型形成的训练集预测值{Train,Train,…,Train}和测试集预测值{Test,Test,…,Test},分别组合形成第2层模型的训练集和测试集;

使用上述数据集训练二级模型。

2.4 集成元模型序贯采样策略

本节首先明确的集成元模型拟合不确定性检验标准,确定序贯采样点的选择方法;而后在初始采样规模、方法、及序贯采样步骤等方面明确集成元模型的序贯采样策略。

2.4.1 集成元模型拟合不确定性检验方法

通常,使用元模型的情况有两种:一是预测,通过建立元模型预测未知输入情况下系统的响应;二是优化,通过元模型快速分析使系统获得最佳响应的输入条件。对应上述情况,元模型的序贯采样通常包括两种思路:一是寻找元模型拟合精度较差的范围,在该范围内增加采样点,以提高元模型整体拟合精度;二是在现有元模型取得的极值点的附近增加采样点,提高元模型在极值附近的拟合精度。

本文建立集成元模型的目的是生成作战体系能力图谱,需要对大量方案做出预测,因此,需要提高模型在取值范围内的整体拟合精度。对于集成元模型而言,各基元模型的预测能力存在一定的差异,将这种差异定义为集成元模型的拟合不确定性(meta model uncertainty)。文献[24]提出了用多个元模型在设计空间内各点预测值的标准偏差来检验拟合不确定性:

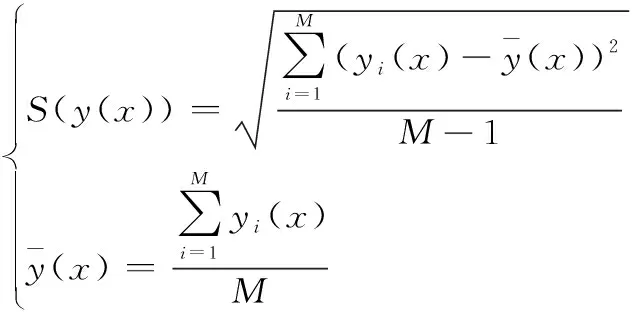
(2)

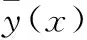
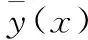
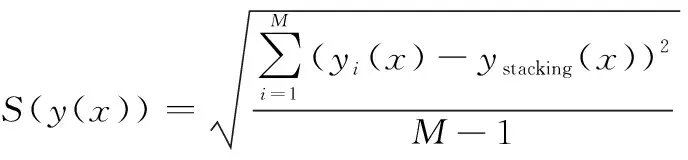
(3)

式(3)计算结果较大的区域表明各基元模型预测差异大,则在该区域增加采样点,以提高预测精度。

2.4.2 初始采样规模

初始采样规模影响直接影响初始模型构建的效率和精度,关于采样规模的研究越来越多。文献[25]比较了不同采样规模对元模型预测精度的影响。文献[26]建议初始采样规模应是问题维度的10倍,文献[27]证明了该建议的可行性。文献[28]建议采样规模为2(+1),其中为问题维度。文献[29]通过对变量空间的角点进行采样,建议初始采样规模为2。文献[30]建议初始采样规模应设置为max{2(+1),01},其中为总评价次数。文献[31]建议采样规模不应超过问题维度的20倍。文献[32]建议如果问题维度小于20维,则采样规模不应超过500;如果问题维度大于20维,则采样规模可大于500。

综合上述分析,由于在作战实验想定方案探索时,通常会聚焦于特定范围,问题维度不会过高,本文初始采样规模选定为问题维度的20倍。

2.4.3 初始采样方法

常用的采样方法有蒙特卡罗采样、正交采样、拉丁超立方采样、均匀采样等。其中,拉丁超立方采样(Latin hypercube sampling,LHS)作为一种全空间的采样方法,是一种以分层采样为理论基础并在此基础上随机均匀布置采样点的采样方法,能够通过较少的样本获得较高的精度,是目前应用最为广泛的一种采样方法。本文采用LHS建立初始训练样本。

LHS的基本步骤如下。

确定采样规模;

将维空间中每个变量(=1,2,…,)的取值范围划分为等大小、等概率的个分层;

在每个变量的各分层中随机抽取一个数值;

将步骤3中各变量随机选取的数值组合,即产生一个样本点;

重复步骤3和步骤4,产生个样本点。

LHS在每个分层进行采样,在采样规模较小的情况下,保证了样本点能够较全面的反应空间的整体信息,此外,其随机抽样的方式无需对样本点规模做出限制,有较强的通用性。

2.4.4 序贯采样步骤

以拟合不确定性为检验指标,指导集成元模型的序贯采样和更新,其基本流程如下。

根据问题维度确定初始采样规模;

按照LHS方法,确定个初始样本点;

调用仿真系统,获取初始样本集;

训练各基元模型和集成元模型;

利用LHS方法,产生个检验点;

利用式(3)计算个检验点上集成元模型的拟合不确定性,寻找集成元模型不确定值最大的个检验点;

调用仿真系统,获取个点的仿真结果,并将该点集及仿真结果作为序贯采样点加入原样本集中,形成新的训练样本集;

重复执行步骤4～步骤7,直至满足收敛条件。

收敛条件根据具体问题,对集成元模型的精度、训练时间或训练次数做出限定,其判断步骤如图3所示。

3 案例分析

3.1 实验设计

3.1.1 实验想定

以红方在某重点关注海域内对蓝方某型时敏目标的指示能力、打击能力的分析任务为背景,生成红方作战体系对该重点关注海域内的作战能力图谱。实验依托“体系仿真试验床”系统进行,红方部署任务区域相关的作战力量,主要包括相关天基预警装备和通信装备、对目标实施打击的远程打击装备,并建立完善的指挥控制体系;蓝方主要包括活动于红方重点关注海域的舰艇目标及相关探测和拦截装备。

3.1.2 实验方案

红方作战体系对重点关注区域的目标指示能力和打击能力随对抗环境的差异在三维物理空间内有不同的分布,并随作战进程的推进不断变化。对该区域按照热图与基于地理信息的可视化方法生成能力图谱,将红方重点关注区域分为×个区块,通过对每个区块进行仿真,计算区块内能力指标(如目标指示能力)数值,根据数值大小对区块进行着色,形成该区域的能力图谱,通过生成不同条件下的能力图谱,分析体系的整体能力。图6为生成体系能力图谱的示意图。

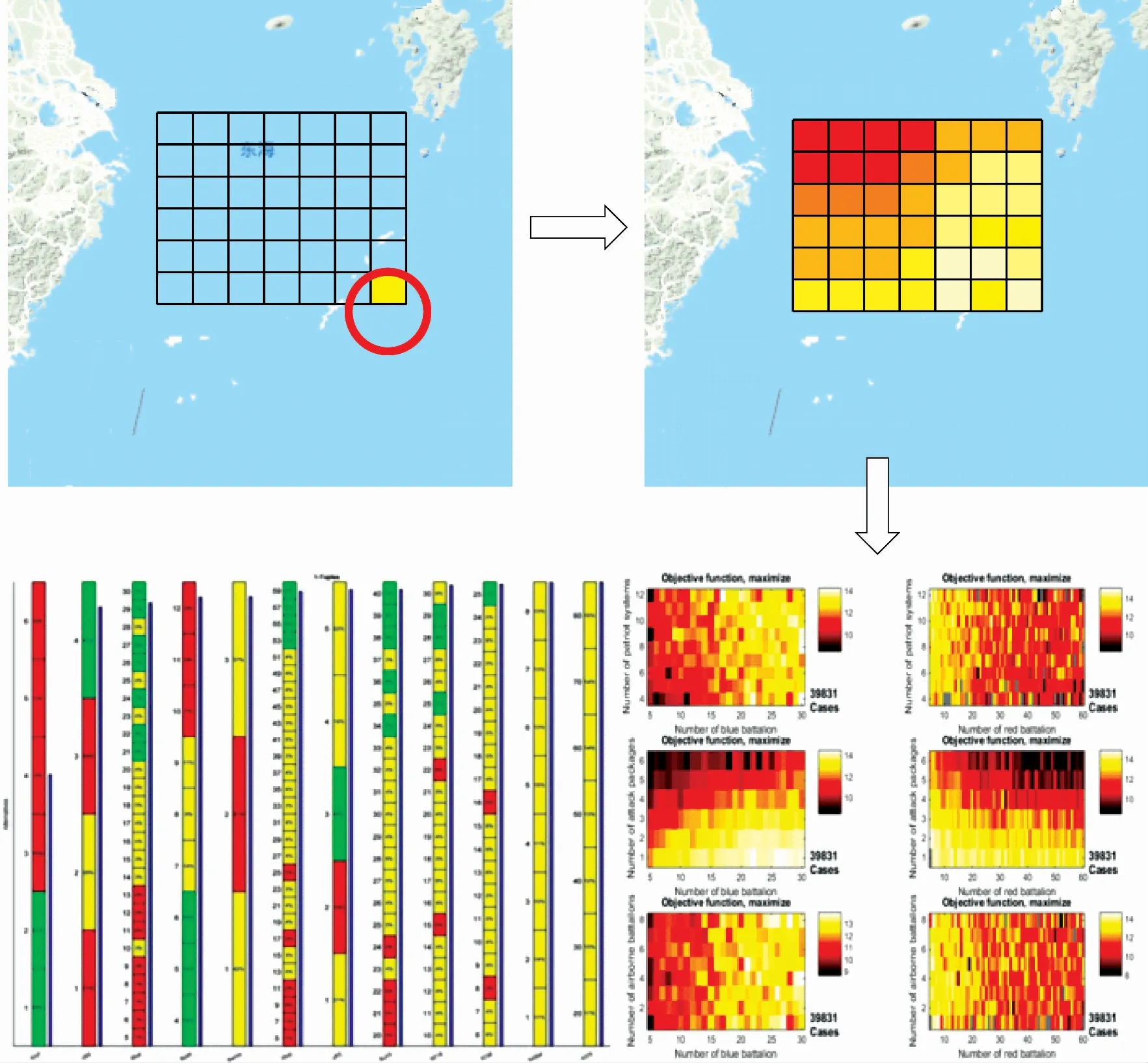
图6 生成作战体系能力图谱示意图Fig.6 Schematic diagram of generating operational system of systems capability graph

使用该分析方法,将本想定的关注区域,按照地理坐标经纬度每一定度数划分为一个区块,共划分52×42个区块,形成2 184组方案,每组方案进行一次仿真实验,实验时分别对目标指示(target indicate,TI)能力、目标打击(target strike,TS)能力指标进行统计。

其中,目标指示能力TI反映了红方体系从发现目标、正确判断目标直至将目标信息发送到武器平台的能力,本文采用一定时间段内武器装备接受到的有效目标指示时长计算该指标,具体方法为

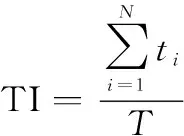
(4)

式中:为有效的目标指示时间段的时长;为有效的目标指示总次数;为作战总时长。

目标打击能力TS反应了红方体系对蓝方目标形成有效毁伤的能力,本文采用对蓝方目标的命中率计算该指标,具体方法为

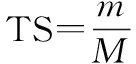
(5)

式中:为红方命中目标的导弹数量;为红方发射的导弹总数。

使用上述数据作为实验数据,建立集成元模型,对元模型的各项性能进行评价。

313 评价指标

在生成作战能力体系图谱的基础上,分别从准确性、鲁棒性两个方面,评价该方法在生成作战体系能力图谱时的有效性。

(1) 准确性指标采用拟合优度为评价指标,计算方法如下：

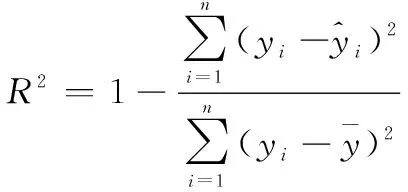
(6)

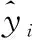
分析本文提出方法在生成作战体系能力图谱的应用中相比于其他模型的预测精度。

(2) 鲁棒性指标计算

(7)

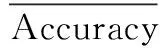
计算该模型对于目标指示能力TI和目标打击能力TS两种不同应用时的鲁棒性指标,分析模型对不同应用环境的适应性。

式(7)以方差衡量数据离散程度,在计算元模型对不同应用场景的预测精度的基础上,计算各精度值的方差,方差越小,说明元模型对各场景预测精度的离散程度越小,则鲁邦性越强。

3.2 作战体系能力图谱生成

针对TI和TS两种能力,分别各取4种作战态势条件进行分析,共形成8组测试数据。生成作战体系能力图谱如图7所示。

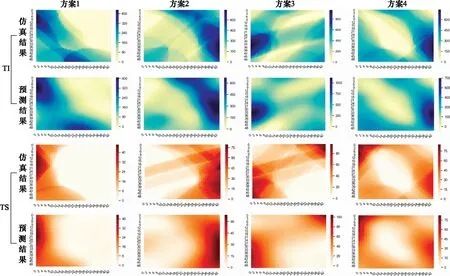
图7 作战体系TI能力和TS能力图谱Fig.7 Capability graph of TI and TS of operational system of systems

图7中,第1行和第3行为不同案例下体系TI能力和TS能力的仿真实验结果,第2行和第4行分别为使用Stacking集成元模型对相应案例的预测结果,实验时设定集成模型预测精度达到90%,或序贯抽样次数达到10次停止训练。从图7中可以看出,在不超过10次序贯抽样的条件下,预测模型能有效反映出体系能力的整体趋势。

3.3 准确性分析

为消除随机误差,对每组样本各训练20次,统计在各组测试数据条件下,的均值、标准差,具体数据如表1所示。

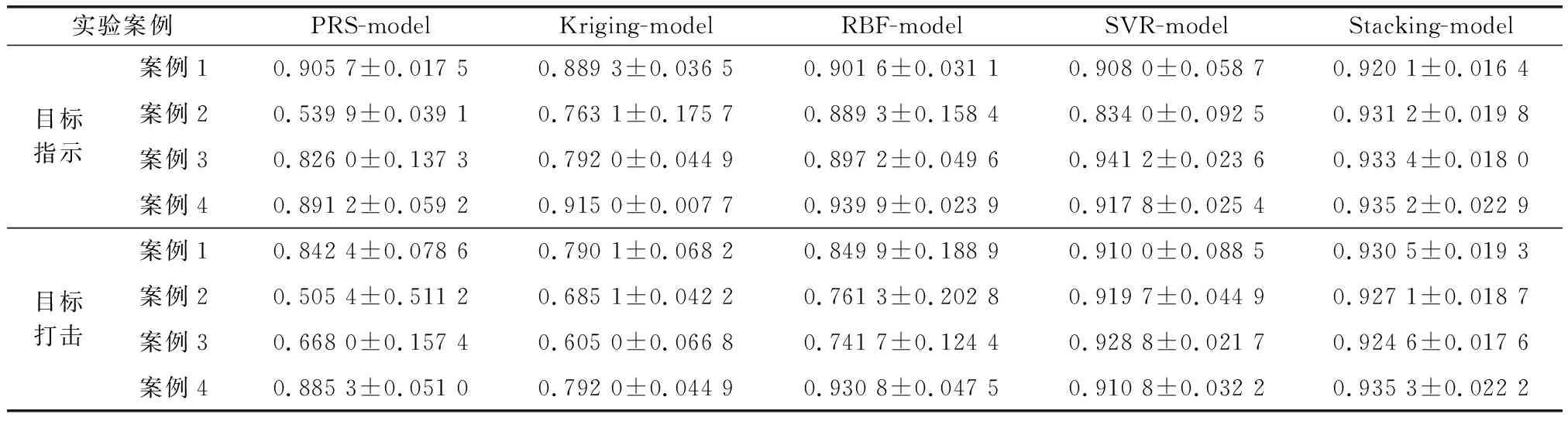
表1 各元模型对不同应用案例的预测准确性

从表1中可知,本文提出的Stacking集成元模型在大多数情况下都能表现出最好的预测准确性,在TI和TS种能力的案例3中,SVR元模型预测准确度略高与Stacking集成元模型,但仅分别高出0.007 8和0.004 2,相差不大,且Stacking元模型在多次运行中的方差较小。各元模型在不同应用案例下的预测准确性分布如图8所示,可见,在不同应用案例下,Stacking集成元模型均有较好的表现。

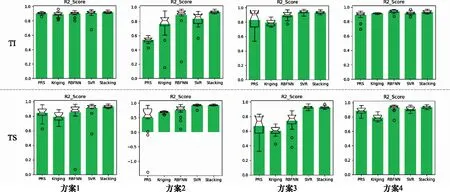
图8 各元模型对不同应用案例的预测准确性分布图Fig.8 Prediction accuracy distribution of each metamodel for different application cases

3.4 鲁棒性分析

根据式(7),分别计算各元模型在TI和TS两种应用下对4个不同方案预测准确度的鲁棒性,并综合计算各元模型对8个方案的鲁棒性,其值如表2所示。可知,本文提出的Stacking集成元模型对各数据集的预测准确度的鲁棒性最强,说明与其他模型相比,该模型在各场景的应用中,预测精度较为稳定。

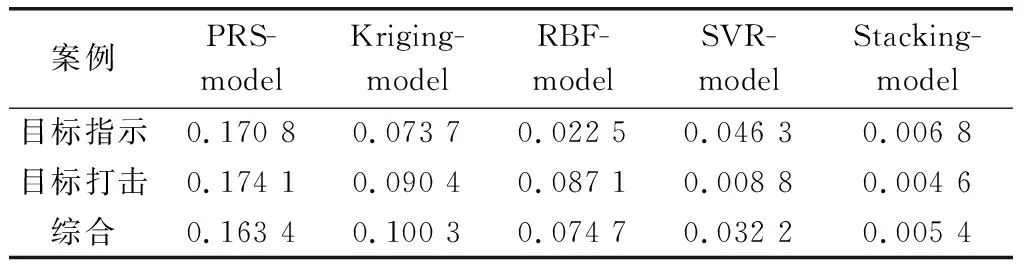
表2 各元模型在不同案例中的鲁棒性

4 结 论

作战体系能力图谱是通过可视化的方法对体系能力进行整体分析的有效手段。生成作战体系能力图谱需要对海量实验方案进行仿真,难以满足时效性要求。本文提出了基于Stacking集成元模型的作战体系能力图谱生成方法,一方面通过Stacking集成学习解决元模型在不同应用条件下鲁棒性较差的问题,另一方面通过使用序贯采样策略解决精度与效率的矛盾问题。通过实验分析,证明了方法的有效性,为快速准确生成作战体系能力图谱,分析作战体系能力提供了方法。