子空间约束秩1干扰下的雷达信号检测

邹 鲲, 来 磊, 骆艳卜, 李 伟

(空军工程大学信息与导航学院, 陕西 西安 710077)

0 引 言

雷达信号检测是雷达信号处理领域中的重点和热点,也是雷达目标搜索、跟踪、识别的基础。为了有效抑制待检测单元背景噪声,提高淹没在噪声中有用信号的检测概率,背景噪声的统计信息是必不可少的。但是在雷达检测器设计阶段,背景噪声统计特征通常不能完全被确定。为此人们提出了自适应检测方法,即利用一定数量的参考数据,采用在线的方式估计待检测单元噪声协方差矩阵,从而能够同时实现背景噪声的抑制和有用信号的检测。

雷达信号检测问题属于二元复合假设检验,一致最大势检验并不存在,因此在设计自适应检测算法时,可以采用多种检验准则。如采用标准的广义似然比检验(generalized likelihood ratio test, GLRT)准则,可以得到Kelly广义似然比检验(Kelly’s generalized likelihood ratio test, KGLRT)检测器。还可以采用双步GLRT准则,先假定待检测单元噪声协方差矩阵已知,得到检测器结构,然后利用参考数据获得噪声协方差矩阵的估计值,代入到检测器结构中,可以得到自适应匹配滤波器(adaptive matched filter, AMF)检测器。考虑到GLRT和Rao检测、Wald检测具有渐进一致性,研究者还提出了对应的Rao检测器和Wald检测器,其中Wald检测与自适应匹配滤波器(adaptive matched filter, AMF)具有相同的结构。

经典的自适应检测问题主要针对均匀场景,要求待检测单元和参考数据具有相同的噪声协方差矩阵,即=,其中是参考数据的协方差矩阵,是待检测单元数据的协方差矩阵。在复杂电磁环境中,参考数据受到污染,有可能使得≠,这种非均匀场景会导致检测性能明显下降。部分均匀场景是非均匀场景中的一个特殊情况,即=c,其中是一个未知的常数因子,那么利用GLRT准则可以得到自适应相干估计器(adaptive coherence estimator, ACE)检测器。而对于非均匀场景,人们提出了很多模型,如广义特征关系模型、贝叶斯统计模型等。而对于雷达信号检测而言,通常还会面临各种干扰,某些干扰也会导致场景的非均匀性,其主要表现为待检测单元噪声协方差矩阵上叠加有一个秩为1的干扰矩阵,或干扰矢量与其共轭转置的乘积形式。可以将这种秩1干扰分为两种类型,一种是假定干扰矢量完全未知,如果待检测单元受到秩1干扰,得到的检测器正好就是ACE。如果待检测单元和部分参考数据受到秩1干扰,可以采用循环优化的方法得到随机噪声覆盖脉冲检测器(random noise cover pulse detector, R-NCP-D)。如果待检测目标是子空间信号,可以采用降维的方法。另一种是假定干扰矢量方向已知,但幅度未知,得到的检测器与KGLRT相差一个数据相关的因子,这种模型还可以用于增强检测器稳健性。

在电子对抗环境,干扰信号的部分先验信息可以利用辅助通道或其他方式获取,为此本文假设干扰矢量约束在某个已知的子空间内,而子空间的维度表示了干扰矢量先验信息的多少。如果该子空间维度为1,相当于干扰矢量方向已知而幅度未知的情况。如果该子空间维度等于信号子空间,则相当于干扰矢量完全未知的情况。本文的主要工作是采用双步广义似然比检验(2-step generalized likelihood ratio test, 2SGLRT)检验准则,推导了子空间约束的秩1干扰检测器(subspace constrained rank one interference detector, SC-ROID)。在满足某种近似条件下,推导了一种降维ACE(rank-reduced ACE, rr-ACE)检测器,从而有效降低计算量。计算机仿真分析表明,在无干扰或无干扰先验信息时,SC-ROID的检测性能与ACE相同,而在其他情况下,SC-ROID相比于其他经典的自适应检测器具有更好的检测性能。而rr-ACE在小样本条件下具有较好的检测性能。

1 检测问题

考虑雷达系统具有的接收通道,利用个脉冲回波进行目标的探测,那么对于第个距离单元,其射频回波经过下变频、正交双通道解调和匹配滤波,可以用一个=×的复矢量表示。设定待检测单元(cell under test, CUT)是第0个距离单元,参考数据来自第1,2,…,个距离单元。本文假定参考数据矢量服从零均值,杂波协方差矩阵为的复高斯分布,其中为维Hermitian正定矩阵且未知。待检测单元数据也服从复高斯分布,但受到二阶秩1干扰,即协方差矩阵表示为+,其中是一个维、约束在某个已知子空间内的干扰矢量,即=,其中干扰子空间由×列满秩矩阵的个列向量张成,表示干扰矢量在该子空间内的坐标。考虑待测的信号为幅度的导向矢量,其为维已知复矢量。综上所述,自适应检测问题为

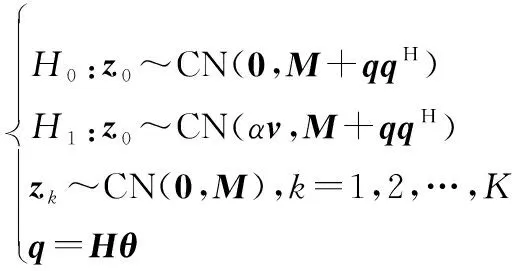
(1)

式中：CN(,)表示均值为,协方差矩阵为的复高斯分布。在该检测问题中,未知参数包括了信号复幅度,噪声协方差矩阵,干扰矢量在子空间内的坐标。

采用2SGLRT准则设计检测器,首先假设噪声协方差矩阵已知,推导似然比结构。在假设下的似然函数可以表示为

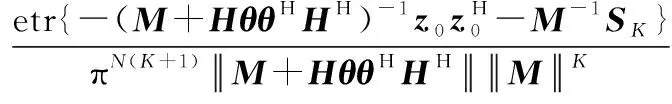
(2)

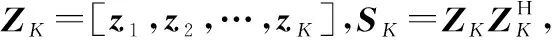
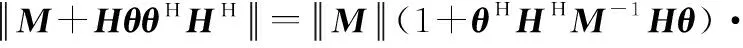
(3)

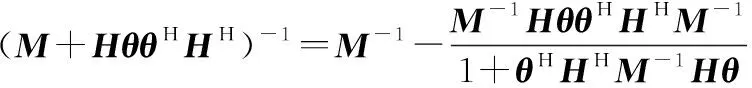
(4)

似然函数可以进一步表示为

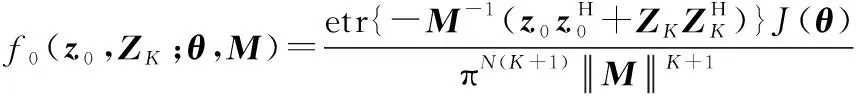
(5)

其中,

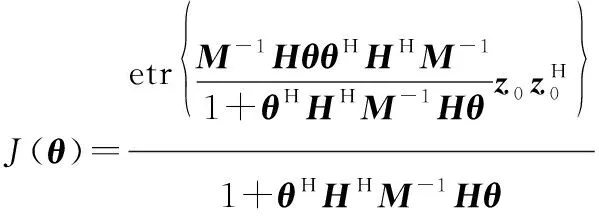
(6)

因此有

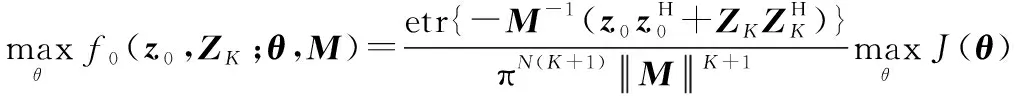
(7)

令==,那么由式(6)可得

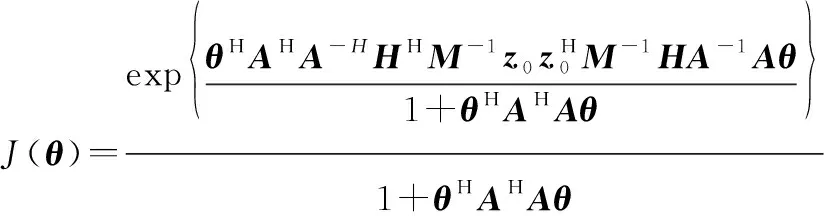
(8)

令=,且=-,可以得到

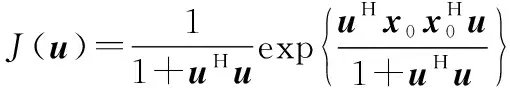
(9)

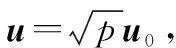
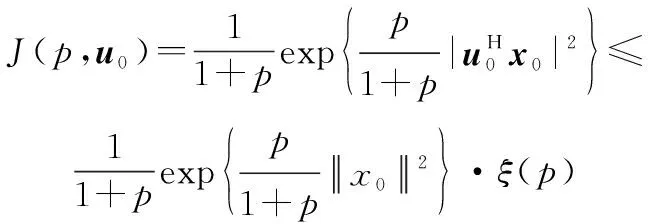
(10)

其中取等号的条件是

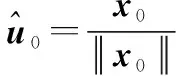
(11)

对式(10)取导数,并令导数为0,容易得到参数的估计值

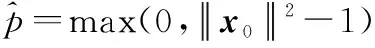
(12)

由此得到

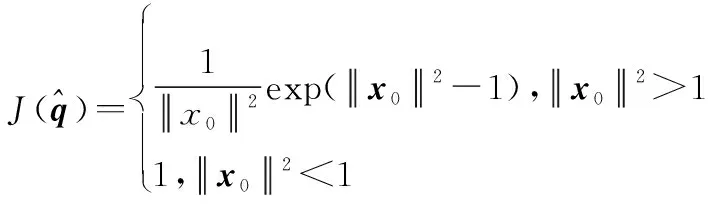
(13)

将式(13)代入到式(14)中,并展开得到

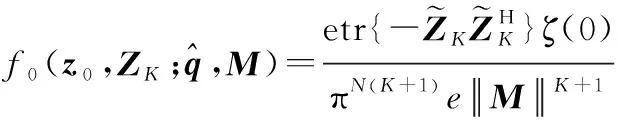
(14)

其中,

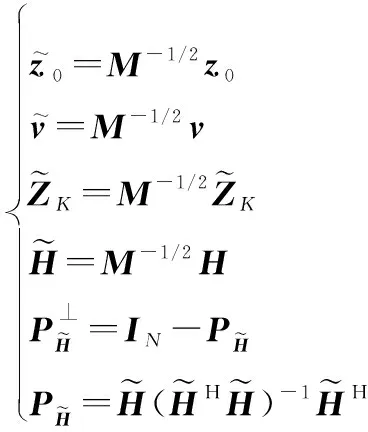
(15)

以及

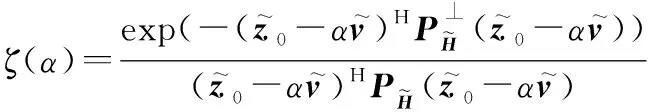
(16)

再考虑H下的似然函数,利用前面的结论,条件似然函数可以表示为

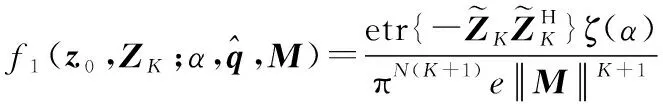
(17)

由此可见:

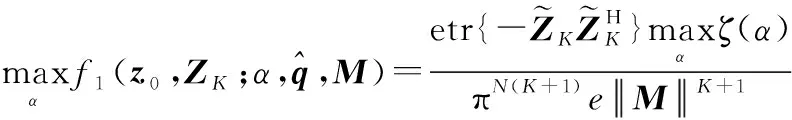
(18)

对单变量函数()求自然对数,并求导,令导数为0,可以得到

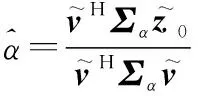
(19)

其中，

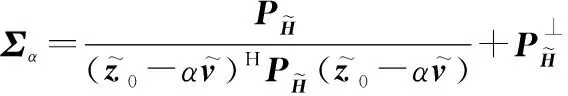
(20)

参数可以通过不动点估计方法获得。再利用参考数据可以获得的估计为

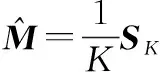
(21)

由此可以构成检测器结构:

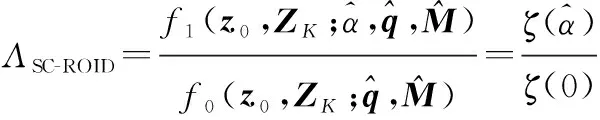
(22)

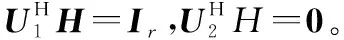
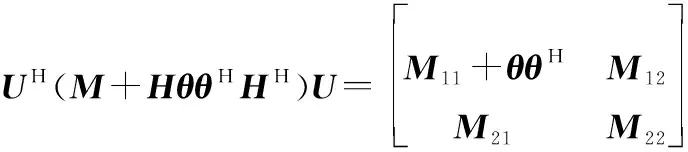
(23)

如果经过酉变换后,噪声仍旧具有较强相关性,即可以假设和近似为零矩阵,假设检验问题可以表示为

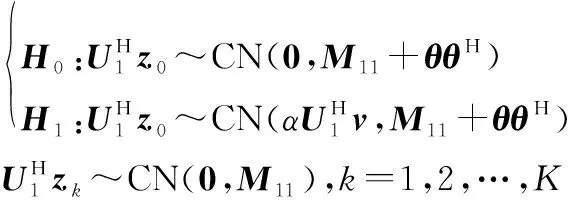
(24)

此时假设检验问题就退化为无子空间约束的秩1干扰检测问题,相对于原问题而言,信号维度从降低为,由此利用文献[14]的结论,可以得到rr-ACE

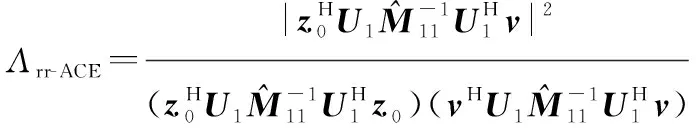
(25)

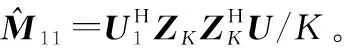
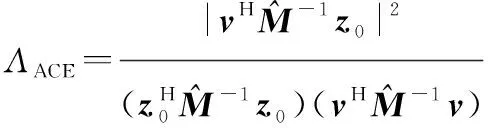
(26)

2 检测性能分析

本文采用蒙特卡罗仿真分析检测性能,基于Neyman-Pearson准则,计算指定虚警概率的检测门限,再计算给定信噪比(signal to noise ratio, SNR)条件下的检测概率。门限的计算采用了100次独立仿真获得,检测概率的计算则是采用了1 000次独立仿真获得。在仿真噪声数据过程中,噪声包含了白噪声分量和相关噪声分量构成,对应的噪声协方差矩阵包含白噪声协方差矩阵和相关噪声协方差矩阵两个部分叠加:

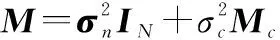
(27)

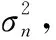
SNR=||

(28)

干扰与噪声的功率比(interference to noise ratio, INR)则定义为

INR=E[||]

(29)

秩1干扰约束在已知子空间内,子空间由矩阵的列矢量张成。

在进行检测性能对比分析时,还考虑了匹配滤波器(matched filter, MF)、KGLRT和AMF。匹配滤波器是假定待检测单元噪声协方差矩阵和干扰矢量完全已知的情况,其检测器性能可以作为所有自适应检测器的上限。检测性能仿真分析参数中,=8,检测门限依据虚警概率=10进行选取。子空间的维度=4,=[,×-],导向矢量=[1,ej2π,…ej2π(-1)],其中=04。

首先要分析无干扰情况下,各种检测器的检测性能。图1给出了取不同值情况下的检测性能对比。图1(a)中=32,此时参考数据数量较多,GLRT和AMF具有类似的检测性能,而SC-ROID的检测性能与ACE相当。图1(b)中=10,此时属于小样本条件,基于参考数据估计噪声协方差矩阵的质量较差,导致了常规检测器性能存在较大的损耗。此时,SC-ROID的检测性能相对于MF而言也有较大的下降,但始终比常规的自适应检测性能好很多。而对于rr-ACE在较小的情况下,检测性能与常规的自适应检测器性能相当。

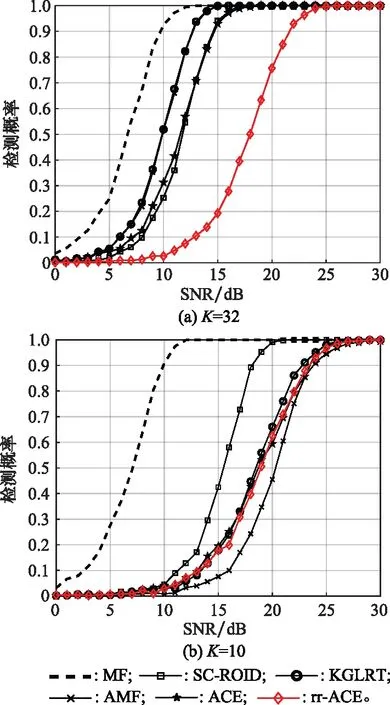
图1 无干扰条件下的检测性能对比分析Fig.1 Detection performance analysis without interference

接下来对干扰较弱的情况进行分析,设置INR=10 dB,图2给出了取值为32和10两种情况下的各种检测器检测性能对比。可以发现当足够大时,如图2(a)所示,SC-ROID检测性能略优于其他自适应检测器性能,而当较小时,如图2(b)所示,可以看出,SC-ROID的检测性能明显有较大的优势。这说明,SC-ROID对干扰强度还是非常敏感的,其优势在小样本条件下尤为明显。同样,在参考数据数量较少时,rr-ACE的性能优于常规的自适应检测器。

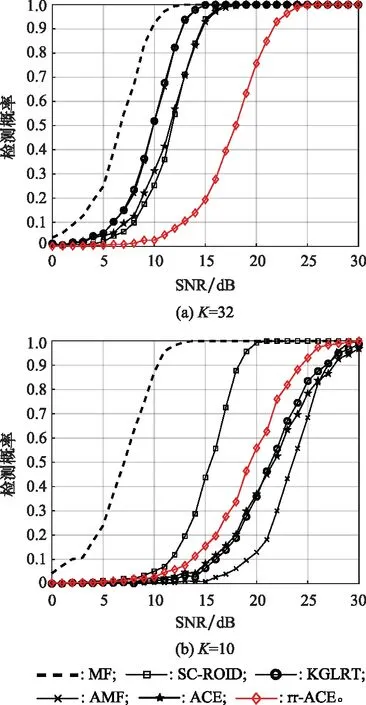
图2 低干扰功率条件下的检测性能对比分析Fig.2 Detection performance analysis with lower interference power

图3给出了INR=20 dB的情况下,各种检测器的检测性能对比分析。由于干扰功率较高,参考数据数量的增加并不能显著抵消待检测单元干扰的影响,导致了常规自适应检测器的性能下降。从图3(b)可以看出,当参考数据数量减少时,常规检测器的性能受到严重影响。但对于SC-ROID检测器,其检测性能始终优于常规检测器。同样,在参考数据数量较少时,rr-ACE的性能优于常规的自适应检测器。

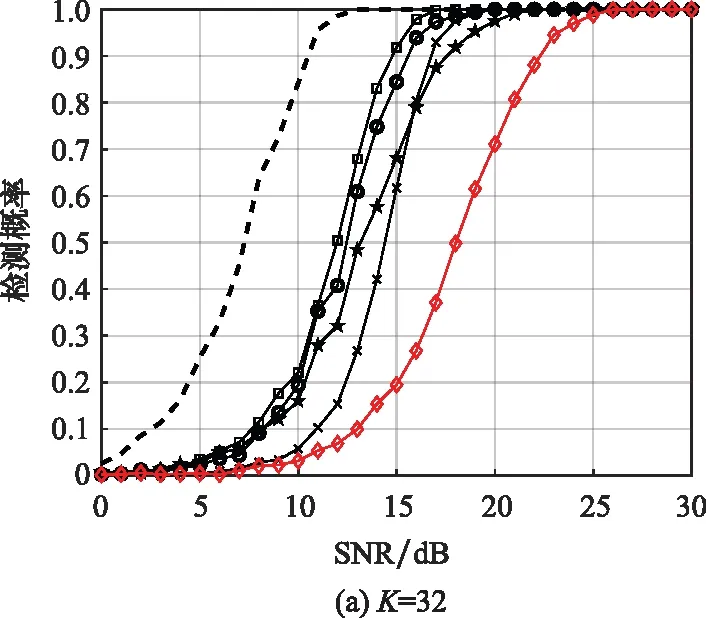
图3 高干扰功率条件下的检测性能对比分析Fig.3 Detection performance analysis with higher interference power

从前文的分析来看,SC-ROID检测性能的提升依赖于干扰先验信息,即已知的子空间。这里考虑=的情况,此时就是一个单位矩阵,表示没有利用干扰的任何先验信息。此时rr-ACE等价于ACE。检测性能分析中,设置INR=20 dB。在这种情况下,无论的取值如何,SC-ROID与ACE的检测性能完全重合,而文献[14]也证明了在无干扰信息情况下,检测问题的检测器就是ACE。进一步还可以发现,当参考数据足够多时,KGLRT的性能是最好的,而当减少时,SC-ROID与KGLRT、ACE的性能一致。

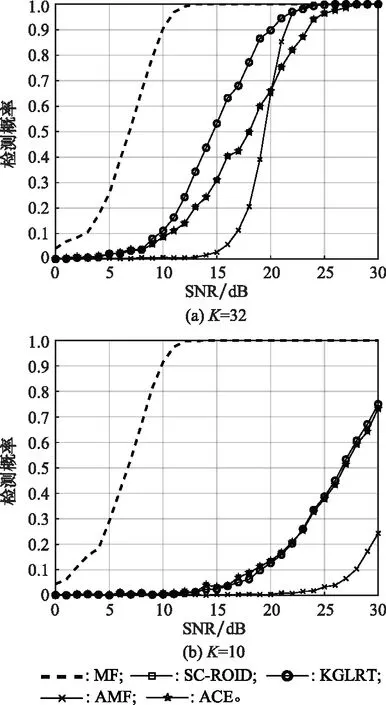
图4 无干扰先验信息时的检测性能对比分析Fig.4 Detection performance analysis without a prior information of interference

3 结 论

本文针对待检测单元受到子空间约束的二阶秩1干扰的自适应检测问题,提出了两种检测方法。采用2SGLRT检验准则,提出了一种新的SC-ROID检测器。利用干扰子空间信息,得到一种可以降低信号维度的rr-ACE检测器。分析结果表明,在无干扰情况或无干扰信息时,SC-ROID检测性能与ACE一致,而在其他情况下,SC-ROID可以利用干扰先验信息提升检测性能,特别是在小样本条件下,SC-ROID较常规自适应检测算法,检测性能有很大的提升。而对于rr-ACE,其主要优点在于计算量更小,且在小样本条件下,检测性能较常规自适应检测器具有优势。