统计与概率易错点分析

丁云

统计与概率的应用在历年中考中一直占有一席之地，所占分值不算很高，难度不大，因此，同学们要尽量拿满分。不过，这块知识内容细碎且繁杂，同学们在解答中容易乱中出错。本文将选取同学们的一些典型易错点进行分析，希望对同学们有所帮助。

一、概念理解不到位

例1 为了增强学生预防新冠肺炎的安全意识，某校开展疫情防控知识竞赛。来自不同年级的30名参赛同学的得分情况如下表所示，这些成绩的中位数和众数分别是 。

【错解】92，96。

【错因分析】本题考查了中位数和众数的概念。解题的关键是掌握求中位数和众数的方法，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）。如果在求中位数时不把数据按要求重新排列，就会出错。因为众数是一组数据中出现次数最多的数，所以只要出现次数最多，那就要把相应数据都写上，特别要注意避免漏写。

【正解】88，84和96。

例2 为了解某市七年级2800名学生的视力情况，从中抽查了100名学生的视力进行统计分析，下列四个判断正确的是（ ）。

A.2800名学生是总体

B.样本容量是100名学生

C.100名学生的视力是总体的一个样本

D.每名学生是总体的一個样本

【错解】A。

【错因分析】本题考查了总体、个体、样本、样本容量的定义。总体是所要考查对象的全体，个体是组成总体的每一个考查对象，从总体中取出的一部分个体叫作这个总体的一个样本，样本容量是一个样本包括的个体数量，样本容量没有单位。我们在区分总体、个体、样本、样本容量这四个概念时，首先找出考查的对象，从而找出总体、个体，再根据被收集数据的这一部分对象找出样本，最后根据样本确定出样本容量。大家容易对总体和个体的意义理解不清而错选，或是对样本容量添加单位导致错选。

【正解】C。

二、概率计算不明晰

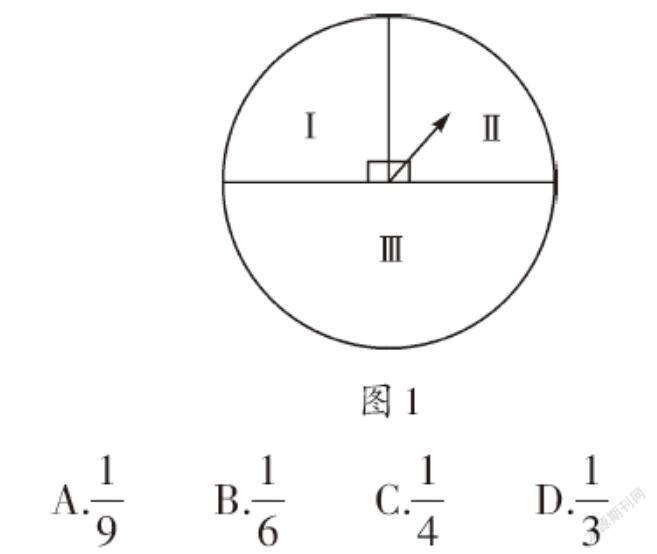
例3 如图1是一个游戏转盘，连续自由转动转盘两次（如果落在分隔线上，则重新转动，直至转到其中一块区域），则两次转动指针都落在数字“Ⅲ”所示区域内的概率是（ ）。

A.[19] B.[16] C.[14] D.[13]

【错解】A。

【错因分析】本题考查的是用列表法或画树状图法求概率。列表法或画树状图法可以不重复、不遗漏地列出所有等可能的结果，适合两步完成的事件。此处需注意：在计算概率时，要关注每一种均为等可能结果，图中“Ⅲ”区域需一分为二，不少同学易在此处出错。

【正解】如图2，把分隔线上方的两个扇形记为A、B，下方的半圆分成两个小扇形记为C、D，画树状图如下：

共有16种等可能的结果，两次转动指针都落在数字“Ⅲ”所示区域内的结果有4种，

∴两次转动指针都落在数字“Ⅲ”所示区域内的概率为[416]=[14]。故选C。

三、角度不明确，答题有缺失

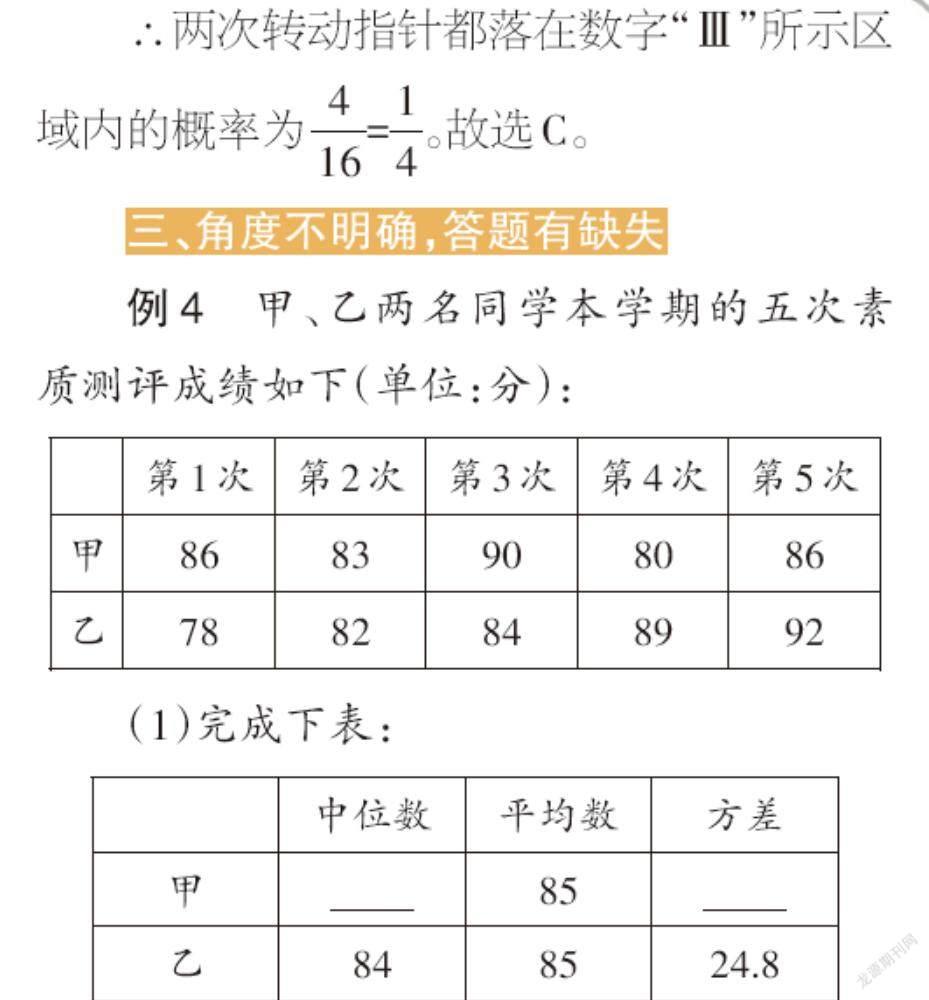
例4 甲、乙两名同学本学期的五次素质测评成绩如下（单位：分）：

（1）完成下表：

[ 中位数 平均数 方差 甲 85 乙 84 85 24.8 ]

（2）请运用所学的统计知识，从两个不同角度评价甲、乙两人的素质测评成绩。

【错解】（2）从平均数看，甲、乙两人水平相当;从中位数看，甲的素质测评成绩比乙好。

【错因分析】本题错误集中在第（2）问，错解一为题中要从“不同角度”，而不是不同数据，同学们需明确各个统计量与数据之间的关系，以此找出多角度;错解二为题中要“评价”，即不仅需要对数据大小进行评价，还需根据关系给出正确的结论，有的同学往往顾此失彼，只比较数据或者只下结论。

【正解】（2）①数据的集中程度：从中位数看，甲的中位数略大于乙的中位数，说明甲的素质测评成绩略好于乙。②数据的离散程度：从方差看，甲的方差小于乙的方差，且两人的平均成绩相同，说明甲的成绩比乙更稳定。③数据的变化趋势：从两人成绩的变化趋势看，乙的成绩在逐渐上升，说明乙进步较大。

（作者单位：江苏省南京市科利华中学棠城分校）