中考题中的“抽签模型”

王向

统计与概率的简单应用是苏科版初中数学的“收官之章”，是同学们经过了“数据的收集、整理、描述”“数据的集中趋势和离散程度”“认识概率”“等可能条件下的概率”等4章内容学习后的实际应用。本章安排了6个具体实例，其中“抽签模型”的考查形式新颖，大家要特别关注。下面选取一些中考题，做简要探讨。

例1 （2021·江苏无锡）将4张分别写有数字1、2、3、4的卡片（卡片的形状、大小、质地都相同）放在盒子中，搅匀后从中任意取出1张卡片，记录后放回、搅匀，再从中任意取出1张卡片。求下列事件发生的概率。（请用“画树状图”或“列表”等方法写出分析过程）

（1）取出的2张卡片数字相同;

（2）取出的2张卡片中，至少有1张卡片的数字为“3”。

【解析】（1）画树状图如图：

共有16种等可能的结果，取出的2张卡片数字相同的结果有4种，

∴取出的2张卡片数字相同的概率为[416]=[14]。

（2）由（1）可知，共有16种等可能的结果，取出的2张卡片中，至少有1张卡片的数字为“3”的结果有7种，

∴取出的2张卡片中，至少有1张卡片的数字为“3”的概率为[716]。

【点评】此题考查的是利用枚举法、列表法或树状图法求概率。其中，树状图法清晰简单，适合两步或两步以上完成的事件;列表法可以不重复、不遗漏地列出所有可能的结果，适合于两步完成的事件。从问题本身来看，本题是一道放回抽卡片的问题，每一次抽到其中任何一张卡片的概率都是相同的，最终的结果也都是等可能的。与一般的抽签问题有共性也有区别，一个人分两次去抽卡片，相当于两个人抽签，前一个人抽完不放回。

例2 （2021·江苏常州）在3张相同的小纸条上，分别写上条件：①四边形是菱形;②四边形有一个内角是直角;③四边形的对角线相等。将这3张小纸条做成3支签，放在一个不透明的盒子中。

（1）搅匀后从中任意抽出1支签，抽到条件①的概率是 。

（2）搅匀后先从中任意抽出1支签（不放回），再从余下的2支签中任意抽出1支签。四边形同时满足抽到的2张小纸条上的条件，求四边形一定是正方形的概率。

【解析】（1）搅匀后从中任意抽出1支签，抽到条件①的概率是[13]。

（2）画树状图如图：

共有6种等可能的结果，四边形一定是正方形的结果有4种，

∴四边形一定是正方形的概率为[46]=[23]。

【点评】这是一个典型的抽签问题，难度不大，通过画树状图能理清等可能的所有结果，再从结果中找到能使事件发生的结果。事件发生的概率=能使事件发生的结果的个数与总结果个数之比。另外，本题在考查概率简单应用的同时也考查了正方形的判定条件，题目形式比较新颖。

例3 （2021·江苏镇江）一只不透明的袋子中装有1个黄球，现放若干个红球，它们与黄球除颜色外都相同，搅匀后从中任意摸出两个球，使得P（摸出一红一黄）=P（摸出两红），则放入的红球个数为 。

【解析】（1）假设袋中红球個数为1，此时袋中有1个黄球、1个红球，搅匀后从中任意摸出两个球，P（摸出一红一黄）=1，P（摸出两红）=0，不符合题意。

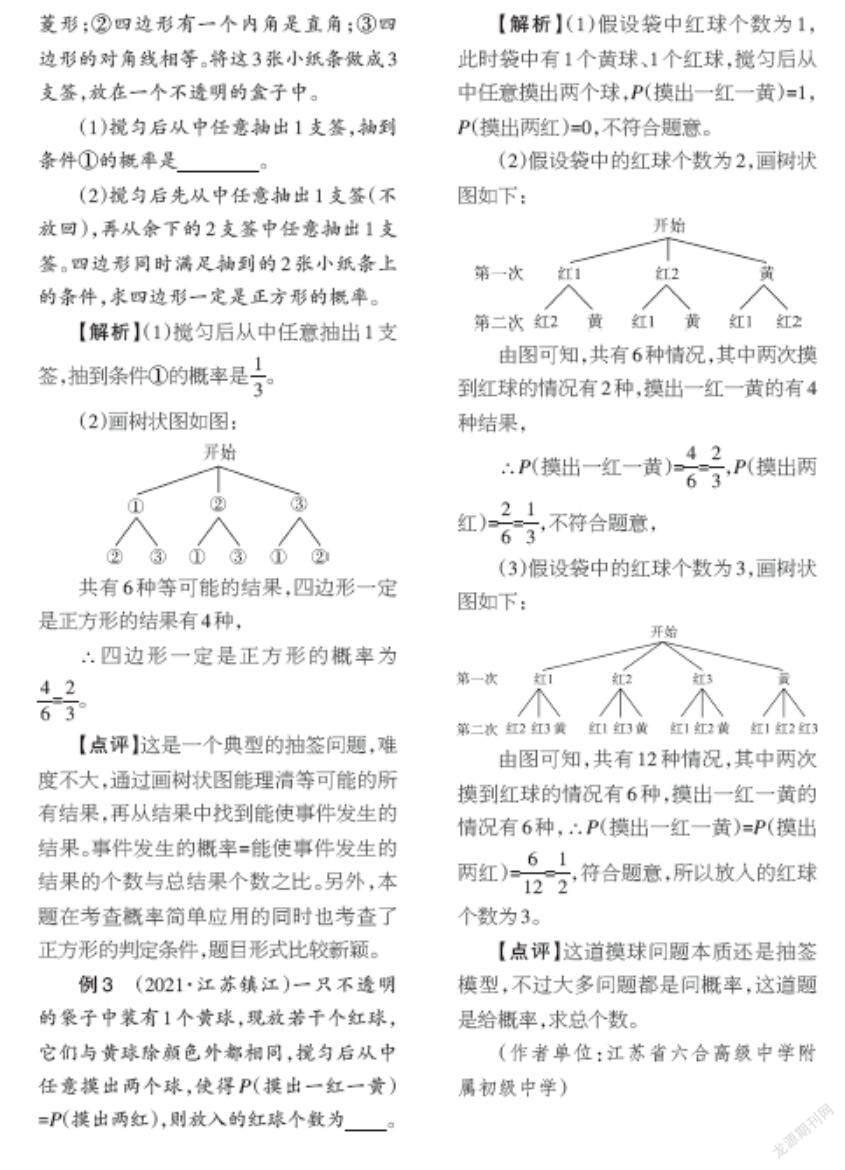
（2）假设袋中的红球个数为2，画树状图如下：

由图可知，共有6种情况，其中两次摸到红球的情况有2种，摸出一红一黄的有4种结果，

∴P（摸出一红一黄）=[46]=[23]，P（摸出两红）=[26]=[13]，不符合题意，

（3）假设袋中的红球个数为3，画树状图如下：

由图可知，共有12种情况，其中两次摸到红球的情况有6种，摸出一红一黄的情况有6种，∴P（摸出一红一黄）=P（摸出两红）=[612]=[12]，符合题意，所以放入的红球个数为3。

【点评】这道摸球问题本质还是抽签模型，不过大多问题都是问概率，这道题是给概率，求总个数。

（作者单位：江苏省六合高级中学附属初级中学）