团簇Mo2S4的极化率与电子自旋密度的计算分析

王 倩，方志刚，秦 渝，井润田，侯欠欠，郑新喜

(辽宁科技大学化学工程学院，辽宁 鞍山 114051)

催化反应常用贵金属附着于纳米材料上进行催化以达到更好的效果，纳米材料良好的吸附性能、更大的分子空隙等优异性能使贵金属得到了最大化使用，纳米团簇是介于原子、分子与宏观固体物质的一种物质结构，近年来一直是量子化学的研究热点之一，其物理、化学性质随团簇分子所含原子数的变化而变化，并且不同的结构性能之间仍存在差异，由于其独特的结构，在磁学、催化及析氢等领域都有相关报道[1-5].目前对于Mo-S体系的相关报道，主要集中于MoS2与Mo6S8以及相关离子[6-9]，而对纳米团簇Mo2S4的极化率与自旋密度这两个方面的研究报道甚少.极化率是衡量团簇分子变形的物理量，是研究团簇结构特征的主要观测指标之一，目前，团簇分子的极化率与其尺寸大小的关系已经进行过一系列实验验证，并得出了一些经验性结论，如：二者呈线性关系，随着团簇尺寸大小的增大，团簇分子的原始极化率也随之增大，在某些特定条件下，二者关系会发生不定的改变[10].本文通过分析团簇分子Mo2S4的极化率、原子的自旋密度以及自旋密度图等来分析其稳定性，得出相关结论，以期补充Mo-S体系在极化率与电子自旋密度理论计算方面的空白，同时为相关实验提供理论支撑.

1 计算方法与优化构型

基于拓扑学原理[11]将6个原子按不同排列组合方式设计出几何模型，如五棱锥、四棱双锥、平面六边形等，同时变换不同的原子位置得出团簇Mo2S4的40种初始构型，并以密度泛函理论[12]为基础，在B3LYP/Lanl2dz水平下[13]对团簇Mo2S4的初始构型进行全参数优化计算及虚频验证，计算过程中采用Hay等[14]的18-eECP双ξ基组(3s，3p，3d/2s，2p，2d)计算方法对Mo原子进行计算，采用Dunning/Huzinaga双ξ基组(9s，5p/3s，2p)计算方法并考虑极化函数ξS.d=0.55对S原子进行计算[15].排除含虚频的不稳定构型及同重态下相同几何构型中能量较高的构型之后，分别得到单、三重态的优化构型各5种.所有计算均在启天M4390计算机上利用Gaussian09程序完成.

以能量最低的构型1(3)为参考，设其能量为0 kJ·mol-1，并按照各稳定构型的相对能量高低排序，画出各稳定构型图，如图1所示，其中右上角标括号内的数值表示构型的自旋多重态，构型下方数值表示各构型相对能量.

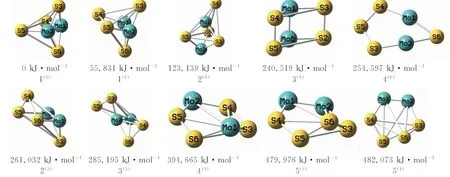
图1 团簇Mo2S4的优化构型Fig.1 Schematic illustration of optimized configurations of cluster Mo2S4

2 结果与讨论

2.1 极化率

在外电场作用下，团簇分子会表现出团簇极化率的各向异性，极化率的各向异性不变量(Δα)是反映这一表现的物理量，它是团簇分子在外电场中的响应，Δα越大，其结构越易受到外电场的影响，构型极化率的各向异性越大.随着外电场的变化，原子或分子的电子云形状会随之发生改变，极化率(〈α〉)是衡量团簇分子结构在外电场作用下变形程度的主要观测指标之一，在一定程度上反映出所处空间电子分布的情况及极化过程的难易程度.团簇极化率越小，则其结构越紧凑，原子间的相互作用越强，在外电场作用下越不易发生形变，保持其原本的电子云分布.通过公式(1)、(2)[16]计算得团簇Mo2S4各优化构型的极化率(〈α〉)及极化率的各向异性不变量(Δα).

(1)〈α〉=(αxx+αyy+αzz)/3 ;

详细计算结果列于表1.可知，构型4(1)与构型4(3)的Δα的值相近且相对较大(分别为115.724、114.156 a.u.)，故相较于其余稳定构型，二者受外电场的影响较大，在外电场的作用下极易发生形变，构型的各向异性较大.此外，构型2(1)的极化率值最小，故其结构最为紧凑，原子间的相互作用力最强，在外电场的作用下不容易变形.同为单重态不同空间结构的构型1(1)与2(1)极化率相差较大，同为三重态同种空间结构的构型4(3)与5(3)极化率相差不大，不同重态同种空间结构的1(1)与1(3)极化率相差也不大，这在一定程度上说明，团簇分子变形的程度与其空间结构有关.

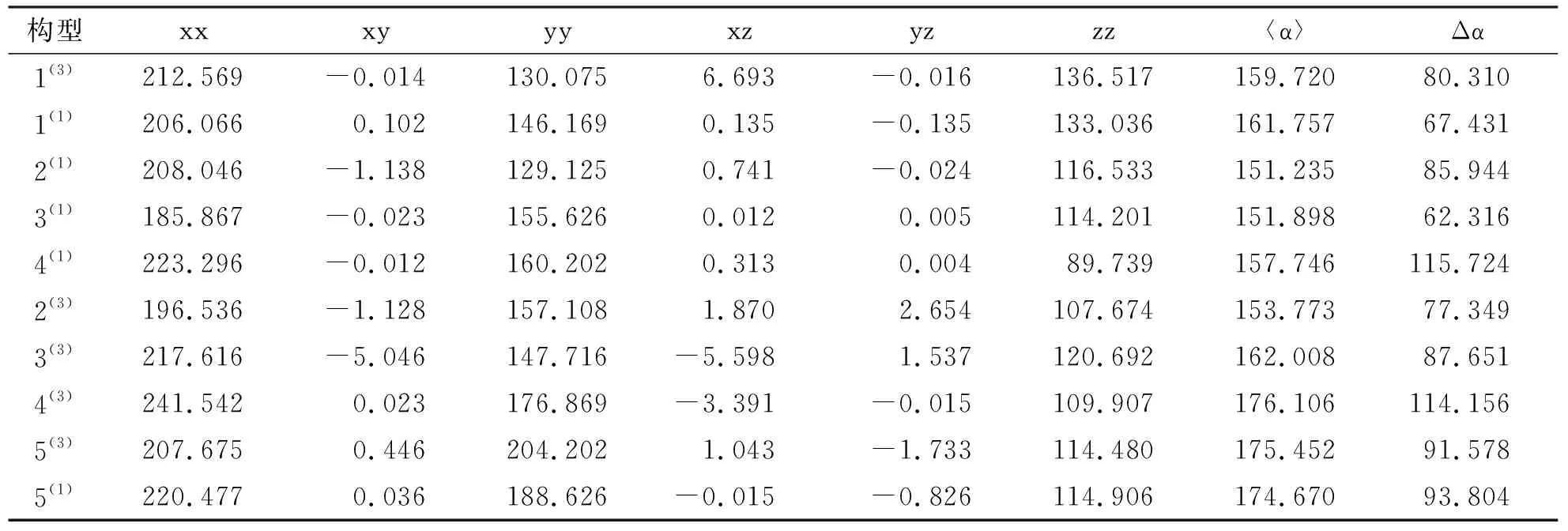
表1 团簇Mo2S4的极化率Tab.1 Polarizability of cluster Mo2S4

2.2 电子自旋密度

由于为闭壳层的单重态构型的自旋空间轨道同等，分子的电子自旋成对，而为开壳层的三重态构型含α、β 2个自旋不配对的电子，分子的净自旋不为0，故本文有关电子自旋相关研究仅对团簇Mo2S4的三重态构型展开.

2.2.1 三重态构型各原子与原子间的电子自旋密度

构型的稳定性会受分子内电子自旋的影响，通过对电子自旋密度数据的计算分析可以解释构型的稳定性.现列出团簇Mo2S4三重态构型各原子的电子自旋密度值，如表2所示，团簇Mo2S4三重态构型原子间的电子自旋密度值见表3，α电子出现的概率用正值表示，β电子出现的概率用负值表示.由α、β电子及二者重叠部分的情况，可以直接反映团簇分子各原子间的成键强度与均匀程度，其电子自旋密度分布越均匀，构型的成键强度与稳定性越好.

由表2可知，最为稳定的构型1(3)的S3与S5原子自旋密度值相等，二者均为负值(均为-0.143)，S4与S5原子自旋密度值相近，二者均为正值(S4:0.045；S5:0.042)，即构型1(3)S原子上的电子自旋密度分布α、β电子均过剩，同理，Mo1与Mo2原子的电子自旋密度均为正值(分别为1.556、0.643)，故其Mo原子上的电子自旋密度分布均为α电子过剩.此外，结合表3可知，构型1(3)的非金属键S—S均为正值，且除非金属键S3—S6外(S3—S6:0.003)，其余非金属键S—S原子间的电子自旋密度值相同(均为0.002)，金属键Mo1—Mo2为负值(-0.035)，金属与非金属键Mo—S有正值也有负值.这说明，对于构型1(3)，各个非金属原子S之间成键时α电子过剩，而金属原子Mo之间成键时β电子过剩，同时金属原子与非金属原子之间成键既有α电子过剩，也有β电子过剩，甚至有二者完全抵消的情况(Mo2—S4：0.000).综上所述，构型1(3)的各原子间成键强度相近，稳定性较好；同理，构型5(3)的各个S原子的自旋密度值并不相等(分别为0.031、0.212、0.048、-0.001)，Mo1与Mo2原子的自旋密度值分别为-1.456与3.166，各原子间的自旋密度值差别较大，故构型5(3)各原子间成键强度不同，稳定性较差.

表2 团簇Mo2S4三重态构型各原子的自旋密度Tab.2 The spin density of the atoms of the cluster Mo2S4 triple-state configuration

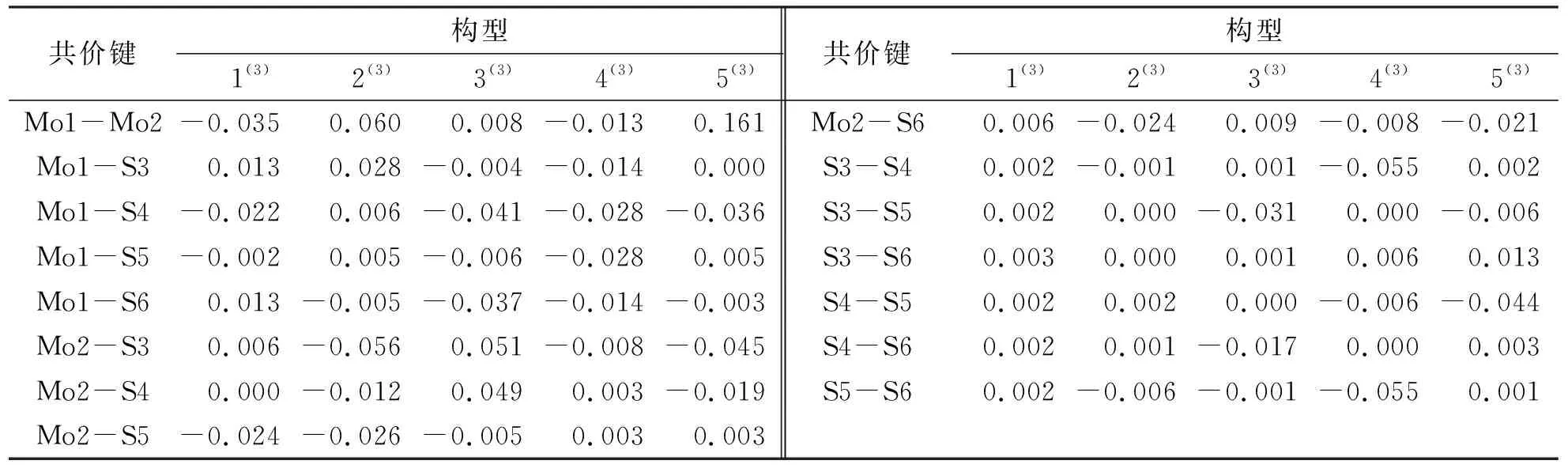
表3 团簇Mo2S4三重态各优化构型原子间电子自旋密度Tab.3 Cluster Mo2S4 triple state each optimizes the electron spin density between the configuration atoms

2.2.2 各构型的稳定性规律分析

绘制团簇Mo2S4三重态构型的电子自旋密度分布图如图2所示，其中浅色阴影部分表示自旋向上的α电子，深色阴影部分表示自旋向下的β电子.现将其大致分为3类讨论(以图1优化构型为参考).

第一类：优化构型对称性良好的构型1(3)、4(3).在图1中，可以明显看出，优化构型1(3)、4(3)都有较好的对称性，由图2可知，构型1(3)、4(3)的电子自旋密度图的对称性也较好，α、β电子分布均匀，同时，结合2.2.1可知，构型1(3)、4(3)外围电子自旋密度分布均匀，各原子间成键强度相近，稳定性较好.

第二类：未具有明显对称结构的构型2(3)、3(3)与构型5(3).构型2(3)、3(3)与构型5(3)均未具有明显对称结构，根据本文所收集电子自旋密度分布图并不能得出一个确定的二者稳定性强弱关系，但在热力学上，构型2(3)、3(3)与构型5(3)的能量是递增的，故其稳定性逐步递减.由此可知，电子自旋密度并不能完全判断构型的稳定性，团簇分子的稳定性并不单一地由电子自旋密度所决定.

第三类：同种几何构型的构型1(3)与构型2(3).如图1所示，构型1(3)、2(3)的几何构型同为四棱双锥，而构型1(3)的对称性优于构型2(3)，这与其不同的原子排序与极化程度都有密切的关系.在图1中，可以明显看出：构型1(3)是由Mo1-Mo2-S4-S5为基准面，S3为锥顶，S6为锥底；构型2(3)是以Mo1-Mo2-S5-S6为基准面，S4为锥顶，S3为锥底；二者的几何构型相同，由于各原子的排序不同，致使二者电子自旋密度分布不同.由图2可知，构型1(3)的电子自旋密度分布图的对称性优于2(3)，故构型1(3)稳定性强于2(3)，这与热力学稳定性的讨论结果相同.

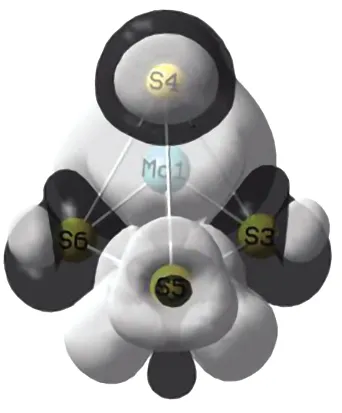
1(3)2(3)3(3)4(3) 5(3)

3 结论

本文通过对团簇Mo2S4分子的极化率及电子自旋密度数据进行计算分析得：团簇Mo2S4分子的变形程度与其空间结构有关；构型结构的稳定性与其外围电子自旋密度分布有关，电子自旋密度分布越均匀，构型的成键强度与稳定性越好；利用电子自旋密度分布图得出的稳定性结果与热力学稳定性的讨论结果有一定的对应关系，但利用电子自旋密度分布图分析也有弊端，当二者的电子自旋密度分布图均未具有明显对称结构时，不能直观地分析出二者的稳定性，即团簇分子的稳定性并不单一地由电子自旋密度所决定.