隐式曲面梯度多孔结构拓扑优化设计方法

孙鹏飞,张跃,尹鹏,刘宏磊,李宝童

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)

多孔结构是结构/功能一体化的优良载体,具有低密度、高比表面积[1]、高比力学性能[2-3]及优良的吸能特性等特点,在航空航天、汽车和医学等领域具有广泛的应用前景。然而,多孔结构的功能特性与其几何构型存在复杂的耦合关系,导致多孔结构设计的复杂度急剧上升。因此,需进一步研究多孔结构的优化设计方法,实现对其功能特性的调控,以满足复杂工程应用的需求。

多孔结构的功能特性取决于其多孔单胞构型与宏观材料分布形式。随着结构设计方法的快速发展,例如计算机辅助设计法[4]、图像法[5]、隐式函数法[6]和拓扑优化法[7-8]等,丰富了具有良好力学性能的多孔单胞构型。相比之下,由隐式函数法设计的多孔单胞具有参数化、设计便捷、可设计性强等优点。作为典型的隐式参数化模型,具有零平均曲率的极小曲面引起了相关领域的广泛关注[9-10]。根据极小曲面在空间周期延伸的维度,可将其分为单周期极小曲面、双周期极小曲面和三周期极小曲面(TPMS)。其中,三周期极小曲面广泛存在于自然界中,例如蝴蝶翅膀、甲虫外骨骼等[11],因其几何构型呈现出独特的对称性,具备高比强度、轴对称刚度、孔洞连通性和良好的吸能特性等优点[12-13]。然而,现有极小曲面的研究侧重于构型的拓扑以揭露其物理特性[14],难以充分发挥其性能优势。此外,梯度多孔结构作为一种材料梯度分布的多孔结构,其功能特性呈现出渐进性和局部性的变化。相比于均匀多孔结构,梯度多孔结构在提升结构刚度、抗屈曲能力[15]和吸能特性[16]等方面有明显的优势。因此,为确定梯度多孔结构的最优材料分布,需进一步研究多孔结构的优化设计方法。

近年来,采用拓扑优化方法对梯度多孔结构进行优化设计已成为一种趋势[17-18]。在本质上,拓扑优化和梯度多孔结构都考虑材料属性的连续性变化[19-20],且在已知载荷和边界条件下,拓扑优化能够确定梯度多孔结构在空间中最优材料分布形式。为实现多孔单胞的宏观梯度分布,Brackett等将多孔结构的体积分数映射到未惩罚的固体各向同性材料惩罚模型法的中间密度上,得到了梯度多孔结构[21]。在此基础上,还可以桁架单元、六边形蜂窝单元等为代表性体积单胞[22],设计非均匀壁厚的梯度多孔结构[23]。此外,张卫红等将均匀化理论和拓扑优化方法相结合提出一种以宏观结构性能为目标、材料表征体胞构型为变量的梯度多孔结构优化设计方法,实现了多孔单胞构型与宏观材料分布的并行设计[24]。然而,采用拓扑优化对梯度多孔结构进行优化设计时,多孔单胞构型的优化过程复杂、多孔单胞间的连续性难以保障。因此,有必要对多孔单胞的设计方法、多孔结构的连续性展开研究,丰富多孔结构的多样性,释放其工程应用潜力。

为实现多孔单胞构型对多孔结构功能特性的调控,本文提出了隐式曲面梯度多孔结构拓扑优化设计方法。结合数值均匀化法[25]建立隐式曲面梯度多孔结构柔度最小化拓扑优化模型,得到了几何和功能呈梯度分布的隐式曲面多孔结构,并通过数值案例和三点弯曲实验验证了本文所提方法的可行性与有效性。

1 极小曲面多孔结构几何建模

1.1 三周期极小曲面几何描述

三周期极小曲面是一种由隐式水平集函数定义的曲面式结构,具有较强的可设计性。因此,本文采用极小曲面作为梯度多孔结构的代表性体积单元。为控制极小曲面的体积分数,在其隐式水平集函数中引入水平参数t,如下式

ΦP=C(X)+C(Y)+C(Z)-t

(1)

ΦG=C(X)S(Y)+C(Y)S(Z)+C(Z)S(X)-t

(2)

ΦI-WP=-C(X)C(Y)-C(Y)C(Z)-C(Z)C(X)-t

(3)

式中:C(·)为余弦函数;S(·)为正弦函数;X=2πx/L,Y=2πy/L,Z=2πz/L,x、y、z为高维物理空间坐标;L为单胞尺寸。式(1)～(3)分别为Primitive(P)型曲面、Gyroid(G)型曲面和I-Wrapped Package(I-WP)型曲面的四维隐式水平集函数,根据水平集函数定义,可得到极小曲面的实体区域。

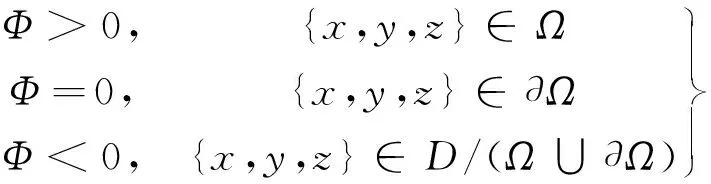
(4)

式中:Φ是极小曲面隐式水平集函数;Ω是曲面实体区域;∂Ω是曲面边界;D是包含实体区域和曲面边界的空间。极小曲面多孔结构隐式建模过程如图1所示。

图1 极小曲面多孔结构隐式建模过程Fig.1 The implicit modeling of TPMS

在极小曲面四维隐式水平集函数中,t代表水平集函数的一个水平面,通过改变水平参数t可以改变水平面到体心的距离,实现实体区域大小变化,从而控制多孔结构的体积分数。当t极大或极小时,极小曲面会出现断裂现象,导致结构在欧式空间中不连续,极小曲面多孔结构如图2所示。

(a)P型曲面(b)G型曲面 (c)I-WP型曲面图2 极小曲面多孔结构Fig.2 TPMS-based cellular structures

在极小曲面隐式水平集函数中引入罚函数,获得如图3所示的极小曲面骨架结构,保证极小曲面多孔结构在小体积分数下具有良好的连续性,表达式如下

(5)

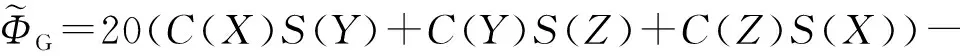
(6)

C(Z)C(X))-(C(2X)+C(2Y)+C(2Z))-t

(7)

(a)P型曲面(b)G型曲面 (c)I-WP型曲面图3 极小曲面骨架结构Fig.3 TPMS-based skeleton structures

1.2 多孔结构混合参数化建模

拓扑优化方法设计的结构几何构型复杂,构造几何参数驱动模型梯度渐变是梯度多孔结构优化设计的基础。图4给出了三周期极小曲面参数化模型。为实现极小曲面与拓扑优化的结合,对极小曲面隐式水平集函数线性加权,构造了混合水平集函数

(8)

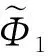
图4 三周期极小曲面参数化模型Fig.4 The parameterized TPMS models

根据参与建模的极小曲面类型和构造方法,将所设计的极小曲面多孔结构分为实心多孔结构、空心多孔结构和混合多孔结构。本文采用I-WP型和P型两种极小曲面进行混合建模。

为建立空心多孔结构参数化模型,对式(8)与同类型极小曲面隐式水平集函数进行差集布尔运算,得到空心多孔结构数学表达式ΦH。差集布尔运算数学表达式为

(9)

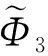
为获得混合多孔结构,对两种极小曲面的混合水平集函数进行并集布尔运算,得到混合多孔结构的数学表达式Φhyb。并集布尔运算数学表达式为

(10)

2 三维数值均匀化法

三维数值均匀化法广泛应用于计算周期性多孔微结构的宏观等效属性。基于数值均匀化法的变密度拓扑优化方法能够生成大量中间密度,满足多孔结构的材料分布需求。因此,本文采用三维数值均匀化法计算极小曲面多孔结构的宏观等效弹性张量。

2.1 极小曲面多孔结构等效弹性属性分析

基于均匀化理论,极小曲面多孔结构的等效弹性张量可表示为

(11)

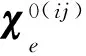
为得到扰动位移χij,构建均匀化平衡方程的矩阵形式如下

Kχij=fij

(12)

刚度矩阵为

(13)

虚拟载荷为

(14)

式中:Be为单元应变-位移矩阵;εij为6个单位应变,ε11=(1,0,0,0,0,0)T,ε22=(0,1,0,0,0,0)T,ε33=(0,0,1,0,0,0)T,ε12=(0,0,0,1,0,0)T,ε23=(0,0,0,0,1,0)T,ε13=(0,0,0,0,0,1)T。

将扰动位移代入式(11),得到多孔结构的宏观等效弹性张量。由于极小曲面多孔结构为体心立方结构,具有高度对称性,其宏观等效弹性张量为6×6的对称矩阵,仅有3个独立变量,简化形式如下式

(15)

2.2 基于径向基函数的参数化等效弹性属性

径向基函数由于其插值效率高、收敛性好、插值系统解的唯一性等优点,被广泛应用于离散数据的插值拟合[26-27]。宏观等效弹性张量关于混合权重因子的函数曲线如图5所示。采用径向基函数建立多孔结构宏观等效弹性张量关于权重因子α的函数,表达式如下

(a)P型多孔结构

(b)I-WP型实心多孔结构

(c)I-WP型空心多孔结构

(d)I-WP&P型混合多孔结构图5 宏观等效弹性张量关于混合权重因子的函数曲线Fig.5 Function curves of the macroscopic equivalent elasticity tensor with respect to the hybrid weight factor

(16)

(17)

其中γ是形状参数,即水平集网格体积的倒数。

同理,基于高斯径向基函数建立多孔结构体积分数关于权重因子α的函数V(α)表达式如下

(18)

式中:vi为扩展系数,本文为体积分数。体积分数关于权重因子的函数曲线如图6所示。

图6 体积分数关于权重因子的函数曲线Fig.6 Curves of the volume fraction with respect to the weight factor

3 梯度多孔结构高阶连续建模

梯度多孔结构的设计过程中,多孔单胞间的连续性至关重要,良好的连续性有助于降低梯度多孔结构在低连通区域的应力集中[28-30]。

极小曲面的隐式水平集函数通过欧拉网格定义,结构边界为局部水平集函数的零水平面。局部水平集函数可由混合水平集函数进行定义,如下式

(19)

式中:M为混合建模的极小曲面数;X=(x,y,z)为高维物理空间坐标;βj为第j个极小曲面的权重函数,如下式

(20)

其中Ωj为极小曲面j的区域。

(a)权重函数曲线

(b)原始梯度多孔结构图7 局部水平集权重函数Fig.7 The weight function of local level set

局部水平集权重函数如图7所示。由图7b可知,由局部水平集函数直接描述的结构存在几何突变的特征。为保证不同多孔单胞间的光滑过渡,采用Heaviside函数构造局部插值模型,实现了梯度多孔结构的高阶几何连续。局部插值模型数学表达式如下

H(Φj)=

(21)

式中:ζ为一个正极小值,用于避免数值奇异,Δ是Heaviside近似的半带宽。高阶连续局部插值模型如图8所示。

(a)局部插值模型曲线

(b)基于局部插值模型的梯度多孔结构图8 高阶连续局部插值模型Fig.8 The high-order continuity local interpolation model

4 梯度多孔结构优化设计

4.1 拓扑优化模型

为实现极小曲面梯度多孔结构刚度拓扑优化,建立了体积约束下混合权重因子α为设计变量、结构柔度最小化的优化模型,如下式

(22)

式中:N为设计域内的单元数;目标函数J为梯度多孔结构的柔度;K、U和F分别为结构的全局刚度矩阵、全局位移向量和全局载荷向量;V(α)为设计域的体积约束;V0为设计域的体积;f为体积分数。

4.2 灵敏度分析

通过获取目标函数的梯度信息来驱动优化算法有效搜索给定设计域内最优材料分布是拓扑优化中的关键一步[19,31]。在拓扑优化中,梯度信息通常被称为敏度信息。因此,采用基于梯度信息的优化准则算法求解优化模型式(22),需要计算目标函数的梯度信息,目标函数和约束条件对设计变量的一阶导数推导如下。

对于结构柔度,在目标函数中代入结构场平衡方程KU=F,有J(α)=FTU,在确定的载荷条件下F为常量,结构柔度关于设计变量的导数为

(23)

由上式可得

(24)

对结构场平衡方程两边求导可得

(25)

将式(25)代入式(24)中,结构柔度关于设计变量的导数为

(26)

其中

(27)

将式(27)代入式(26)中,结构柔度关于设计变量的导数为

(28)

根据式(16),有

(29)

根据式(17),高斯径向基函数关于设计变量的导数如下式

(30)

5 数值案例及实验分析

本文通过以下数值案例验证多孔结构刚度拓扑优化方法的有效性,每个算例讨论实心多孔结构(方案1)、空心多孔结构(方案2)、混合多孔结构(方案3)3种不同代表性体积单胞的结构柔度最小化问题。假定构成实体材料的弹性模量为1、泊松比为0.3,优化迭代中前后目标函数差值小于0.001或迭代次数达到200次时,优化结束。

5.1 三维悬臂梁结构

5.1.1 数值案例 悬臂梁结构边界条件如图9所示,固定336×42×168的悬臂梁结构左端面,结构右端面下边界处施加F=-1的均布载荷。将宏观结构离散为16×2×8个八节点六面体单元,初始结构体积分数为0.28,开展拓扑优化设计。

图9 悬臂梁结构边界条件Fig.9 Boundary condition of a cantilever beam structure

极小曲面梯度多孔结构如图10所示,优化的结构呈现明显的梯度分布,实现了功能的梯度变化,且满足高阶连续。对于方案1,通过优化权重因子α,初始结构柔度为4 635,优化后结构柔度为1 220,结构刚度提升约为74%;对于方案2,通过优化权重因子α,改变了空心多孔结构壁厚,初始结构柔度为2 857,优化后结构柔度为1 085,结构刚度提升约为62%;对于方案3,通过优化权重因子α,较大体积模量的P型多孔结构向较大剪切模量的I-WP型多孔结构转变,初始结构柔度为1 897,优化后结构柔度为1 268,结构刚度约提升33%。数值计算结果表明,在未优化的初始均匀结构中,多孔结构的刚度性能优劣依次为混合多孔结构、空心多孔结构、实心多孔结构;相比于未优化的均布的极小曲面多孔结构,优化的梯度多孔结构的刚度得到了显著提升。

(a)方案1

(b)方案2

(c)方案3图10 极小曲面梯度多孔结构Fig.10 TPMS-based graded cellular structures

5.1.2 鲁棒性分析 在结构实际工作期间,载荷往往不是恒定的,在非预期边界条件下的结构性能是衡量结构鲁棒性的重要标准。为验证多孔结构的鲁棒性,在非预期载荷的情况下对比了本文的3种方案、均匀结构和传统拓扑优化的实体结构的结构柔度变化。非预期载荷的大小与预期载荷相等,方向沿y轴偏转1.37°,受非预期载荷悬臂梁结构的边界条件如图11所示。在边界条件不变的情况下计算预期与非预期载荷的结构柔度,结果如图12所示。

图11 受非预期载荷悬臂梁结构的边界条件Fig.11 Boundary conditions of the cantilever beam structure with unexpected load

由图12可知,传统实体结构的结构柔度由预期载荷下的1 664升高至1 923,结构柔度上升了259。实心多孔结构的结构柔度由1 219升高至1 416,结构柔度上升了180。空心多孔结构的结构柔度由1 085升高至1 265,结构柔度上升了197。混合多孔结构的结构柔度由1 268升高至1 469,结构柔度上升了201。均匀结构的结构柔度由4 634升高至5 057,结构柔度上升了423。数值计算结果表明,相比传统实体结构和均匀多孔结构,本文所设计的梯度多孔结构在非预期载荷下的结构柔度变化较小,可以保证较高的结构刚度,具有良好的鲁棒性。

图12 预期与非预期载荷的结构柔度Fig.12 Structural compliance under unexpected and expected loads

5.2 三维Michell梁结构

5.2.1 数值案例 Michell梁结构边界条件如图13所示,固定尺寸为294×42×82的Michel梁结构底部两端,结构的上端面中部处施加F=-1的均布载荷。将宏观结构离散为14×2×4个八节点六面体单元,初始结构体积分数为0.28,为简化计算过程,仅对总设计域的右半部分结构开展拓扑优化设计。

图13 Michell梁结构边界条件Fig.13 Boundary condition of the Michell beam

图14给出了Michell梁梯度多孔结构。方案1中初始结构柔度为1 218,优化后结构柔度为310,结构刚度提升约为74%;方案2中初始结构柔度为797,优化后结构柔度为293,结构刚度提升约为63%;方案3中初始结构柔度为625,优化后结构柔度为426,结构刚度提升约为32%。数值计算结果表明,优化的梯度多孔结构的刚度得到了显著提升,且不同代表性体积单胞的Michell梁结构刚度优化程度与对应的悬臂梁结构刚度优化程度基本一致。

(a)方案1

(b)方案2

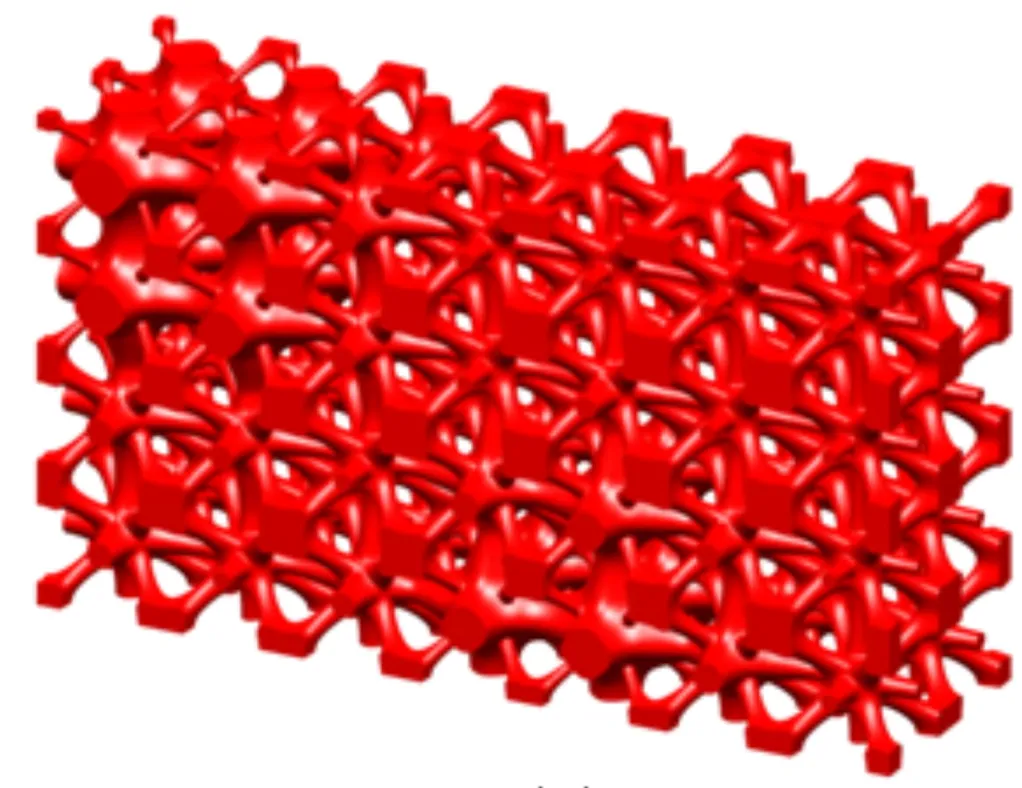
(c)方案3图14 Michell梁梯度多孔结构Fig.14 Michell beam with graded cellular structures

5.2.2 Michell梁结构的三点弯曲实验分析 为进一步揭示梯度多孔MBB梁的力学性能,对3种优化的MBB梁结构、均匀I-WP实体多孔结构进行三点弯曲实验。由于数值案例简化了结构设计域,在进行实验前,通过对称平面将优化结构镜像为完整MBB梁。为保证实验结果的准确性,实验的结构尺寸和体积分数与5.2.1节中数值案例一致。选EOS-P760型3D打印机,采用选择性激光烧结技术,制造了4种MBB梁结构试样,不同方案的3D打印试样如图15所示。结构材料为PA2200,弹性模量为741 MPa,泊松比为0.3,屈服强度为54 MPa。

(a)均匀多孔结构

(b)方案1

(c)方案2

(d)方案3图15 不同方案的3D打印试样Fig.15 3D-printed specimens

在温室条件下,采用万能试验机进行三点弯曲实验,在保证结构边界条件一致的情况下,以50 mm/min的动态载荷加载,加载时间为8 s,不同方案的实验平台如图16所示。

(a)均布多孔结构

(b)方案1

(c)方案2

(d)方案3图16 不同方案的实验平台Fig.16 The experimental platform in different schemes

弯曲载荷-位移曲线如图17所示。由图17可知,4种结构所受到的载荷与位移呈线性变化。相对于均布的I-WP型均布结构,本文所设计的梯度结构的斜率更大,具有更优的承载特性,从而验证了本文方法的有效性。由于实验样件的制造误差以及I-WP实心梯度结构与空心梯度结构的理论柔度相差较小,从而造成两种梯度结构的实验曲线斜率相近,但实验结果的变化趋势符合理论分析的预期。

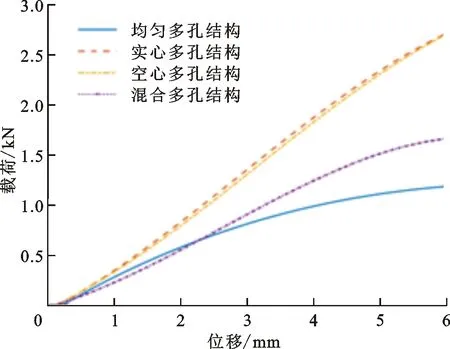
图17 弯曲载荷-位移曲线Fig.17 The load-displacement curves

6 结 论

本文提出了一种隐式曲面梯度多孔结构拓扑优化设计方法。通过混合水平集函数实现了极小曲面多孔结构混合参数化建模。结合数值均匀化法建立柔度最小化的拓扑优化模型,基于局部插值模型,实现了高阶连续的梯度多孔结构优化设计。数值案例和实验结果表明,所设计的梯度多孔结构较均布极小曲面多孔结构具有更优的鲁棒性和承载特性,且单胞构型的不同会造成梯度多孔结构功能特性差异。所提方法能有效实现多孔单胞构型对结构功能特性的调控,丰富了多孔结构的力学内涵。