天然气发动机燃烧不稳定性的多尺度特性分析

2022-02-14丁顺良贺帅峰刘津津宋恩哲杨福源

西安交通大学学报 2022年1期

丁顺良,贺帅峰,刘津津,宋恩哲,杨福源

(1.郑州大学机械与动力工程学院,450001,郑州; 2.哈尔滨工程大学动力与能源工程学院,150001,哈尔滨; 3.清华大学汽车安全与节能国家重点实验室,100084,北京; 4.清华大学车辆与运载学院,100084,北京)

随着发动机排放法规日趋严格,发展高效清洁的替代燃料发动机成为发动机领域的重要发展方向[1]。天然气资源丰富、燃烧清洁,与汽油和柴油相比,燃烧效率高,安全性能好,且燃烧后产生的污染物和CO2大幅减少[2-3]。天然气发动机在稀燃工况下,可以有效降低燃烧温度,进一步减少NOx排放,提高经济性。然而,随着空气量的增加,部分燃烧和失火的可能性增加,循环变动加剧,燃烧不稳定性增强,严重影响了天然气发动机工作性能[4]。因此,揭示燃烧不稳定性产生的机理,研究燃烧过程的动力学规律,对于天然气发动机燃烧优化控制具有重要意义。

天然气发动机是多参数耦合的复杂非线性系统,参数波动及参数间交互作用使燃烧不稳定性的动力学特性呈现出明显的混沌特征。国内外学者采用非线性动力学方法[5]研究了燃烧不稳定性的动力学特性,为燃烧预测控制提供了理论支撑。Sen等采用小波分析和统计分析等方法,对天然气发动机不同工况下的平均指示压力pimep和放热量时间序列进行了分析,揭示了燃烧系统的主要振荡模式,结果表明当燃烧边界参数偏离最佳值时,燃烧系统呈现低频、非随机、振荡的动力学特性,燃烧系统越复杂,呈现的间歇性越强[6-9]。Litak等将多重分形、相空间重构、返回映射、递归图和递归量化分析等方法应用到发动机燃烧不稳定性分析中,发现压力波动主要来源于燃烧的动力学过程,随着混合气浓度变稀,燃烧动力学特性发生显著变化,当前循环的燃烧更容易受到前一循环的影响[11-12]。Daw等采用符号动力学方法分析了不同EGR水平下的pimep时间序列,研究了多缸火花点火发动机稀薄燃烧的不稳定性,结果表明随着EGR水平的增加,缸内混合气浓度变稀,燃烧不稳定性的非随机特征更加明显,当EGR达到一定水平后,多个气缸的波动情况几乎完全一致,说明燃烧不稳定性是确定性过程的结果[13-14]。Finney等采用返回映射、相空间重构和小波分析等方法,对火花点火发动机在4种EGR水平下的放热量时间序列进行分析,结果表明发动机燃烧不稳定性具有较高程度的低维确定性结构,这些确定性效应通常发生在临界燃烧极限附近[15]。李国岫等采用相空间重构和庞加莱截面方法对发动机缸内压力时间序列进行分析,发现缸内燃烧不稳定性存在混沌行为,当量比从化学计量比到稀燃极限变化时,发生了从随机性行为到非线性确定性行为的转变[16]。杨立平等采用相空间重构、返回映射、关联维和LLE等方法,对发动机燃烧不稳定性的非线性特征进行了定性、定量分析,结果表明低负荷工况下发动机燃烧过程更复杂且对初始条件的变化更加敏感[17-18]。

国内外学者对天然气发动机燃烧不稳定性的动力学过程进行了研究,但仍存在一些有待解决的问题:目前研究人员大都是采用非线性动力学方法直接分析天然气发动机的缸压、pimep或放热量时间序列,通过在单一时间尺度上的演化规律来揭示燃烧不稳定性的产生机理,忽视了燃烧不稳定性的多尺度特征,不能全面揭示发动机燃烧过程的动力学规律;或者针对燃烧不稳定性的分析大都转化为对某一全局参数(如pimep)进行循环变动分析,不能全面反应时间序列的频谱特征,无法识别产生燃烧不稳定性的主要频带范围。基于此,本文将天然气发动机的pimep时间序列进行了加性分解,研究信号在不同频带内的波动特征,以揭示天然气发动机燃烧过程在多个时间尺度上的演化途径,结合pimep时间序列的小波分析,揭示了燃烧不稳定性的多尺度周期性振荡规律。这些确定性成分的发现,可提高系统的可预测性,从而降低燃烧不稳定性,扩展发动机稳定运行范围。由于低负荷工况下天然气发动机燃烧不稳定性更明显[18-19],本文针对低负荷工况,以过量空气系数λ为关键影响参数,对天然气发动机燃烧不稳定性进行研究。

1 试验设备及方案

本文研究对象是一台电控多点顺序喷射天然气发动机,表1给出了发动机主要参数。

试验过程中保持燃料量不变,通过调节节气门开度大小来改变λ,采用宽域氧传感器对λ进行实时监测,该传感器的测量精度为0.01。燃烧过程中缸内压力由安装在气缸内部的压电式压力传感器进行测量,测量精度为0.000 1 MPa,通过曲轴转角编码器、燃烧分析仪和计算机等组成的系统进行缸内压力数据采集,其中燃烧分析仪和编码器的测量精度分别为0.025°和0.03°。图1为试验台示意图。

表1 天然气发动机的主要参数Table 1 Main parameters of the natural gas engine

图1 试验台示意图Fig.1 Schematic diagram of the experimental bench

天然气发动机在低负荷工况下燃烧不稳定性更加明显,为了扩展天然气发动机稳定运行范围,研究稀燃极限边界的确定性变化,选取了可在较大λ范围内进行台架试验的转速。因此,测量了转速为1 000 r/min,25%负荷,λ分别为1.0、1.2、1.4、1.6、1.8和1.9时的缸内压力时间序列,每个工况下测量的时间序列长度为连续1 800个工作循环,采样间隔为1°。

pimep表示在一个发动机工作循环内气缸中的平均压力,计算公式如下

(1)

式中:Wc为每个循环对外做的功;Vd为发动机气缸工作容积;p为试验测得的缸内压力。

图2展示了不同λ下的pimep时间序列,从图中可以定性地看出,随λ的增加,燃烧不稳定性加剧,尤其当λ达到1.8后,一部分循环出现了失火状况。

(a)λ=1.0

(b)λ=1.2

(c)λ=1.4

(d)λ=1.6

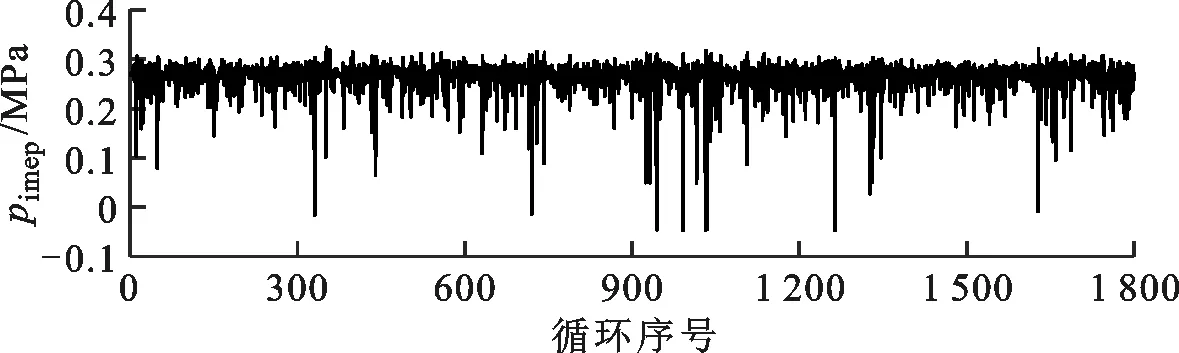
(e)λ=1.8

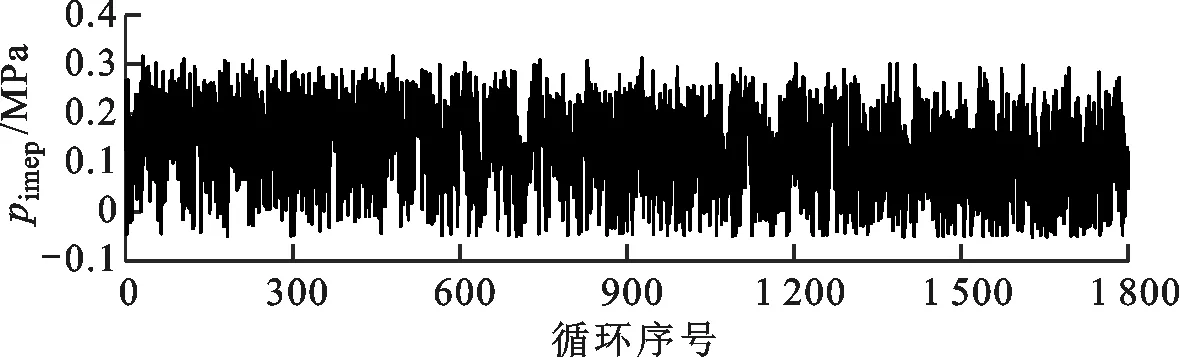
(f)λ=1.9图2 不同λ下的pimep时间序列Fig.2 pimep time series under different λ conditions

2 小波分析

小波分析可将标量时间序列分解到时域和频域的二维空间中,从而确定可变性的主要振荡模式,以及振荡模式随时间的变化规律[20]。小波变换克服了传统傅里叶变换和窗口傅里叶变换的缺点,在时域上取样窗口是根据频率变化而自适应调节的,即在分析低频信号时,窗口自适应变大,分辨率较低,而对于高频信号,窗口自适应变小,分辨率较高。作为一种自适应信号变化规律的时频局部化方法[8],小波分析技术以其独特的自适应调节功能被广泛应用到了各个领域[6-9,20]。小波变换可用于分析在不同频率上包含非平稳功率的时间序列,本文将小波变换应用到天然气发动机pimep时间序列分析中,检测压力波动的周期性和间歇性,确定其随时间变化的趋势,揭示发动机燃烧不稳定性的多尺度振荡特性。

Torrence等提出采用连续小波变换对离散时间序列进行小波分析[21],定义为时间序列xn与小波基函数的卷积,如下式所示

(2)

分析时间序列的周期分量时,通常选用由高斯调制的平面波复Morlet小波作为母小波函数[8],如下式所示

ψ(t)=π-1/4eiω0te-t2/2

(3)

式中:t为无量纲的时间参数;ω0为小波函数的无量纲频率,取6时Morlet小波满足母小波函数条件,同时傅里叶周期T约等于小波尺度因子,T=1.03 s时可以保证时间和频率分辨率之间得到良好的平衡;π-1/4保证了小波函数具有单位能量,不同尺度上的小波变换可直接与其他时间序列的小波变换进行比较。

在使用连续小波变换过程中,须选择一组尺度{sj}来构建完整的图像,对于非正交小波变换,可用2的分数幂来构造一组尺度[21],如下式所示

(4)

式中:N为时间序列的长度;s0为最小可分辨尺度,约为2δt,在分析过程中,将燃烧循环作为时间单位,因此δt取值为1;δ的选择取决于小波函数在谱空间的宽度,δ可取的最大值为0.5,同时δ越小,频率分辨率越高,但会增加计算次数[21],为了更好地均衡计算量和分析结果,将δ设定为0.25。小波功率谱PWPS定义为小波系数模的平方|Wn(s)|2,将小波功率映射到时间和尺度的二维平面中,可用来分析时间序列波动的主要模式。为了方便比较不同λ工况下pimep时间序列的PWPS,本文对PWPS进行归一化处理,归一化后PWPS为|Wn(s)|2/σ2(其中σ2为时间序列的方差),而1/σ2给出了相对于白噪声的功率度量,因此周期性越强,PWPS越高。

图3依次给出了不同λ工况下pimep时间序列的归一化PWPS,影响锥由U型曲线(图3中黑色曲线)隔开,由于边缘效应影响,该U型曲线下方区域的结果不可靠,而U型曲线上方所包围区域表示PWPS中的峰值相对于红色噪声背景光谱达到了95%的置信水平。随着λ的改变,不同频带上的功率谱值出现了规律性的变化,揭示了发动机燃烧循环之间周期性和间歇性的变化规律。当λ=1.0时,40到80个循环周期(图3纵坐标)频带内出现了强功率区域,持续存在于880到1 050燃烧循环(图3横坐标)之间;同时,120个循环周期尺度附近,在1 200到1 450燃烧循环之间出现了较强的功率区域;280个循环周期尺度附近,强功率区域持续存在于800到1 620燃烧循环之间。高功率区域表明天然气发动机燃烧循环之间出现了多时间尺度的周期性波动,波动的频带均位于较低频范围内,而在2到16个循环周期的高频尺度范围内,没有出现周期波动。在该工况下,缸内混合气较浓,点火后产生的初始火核较稳定,火焰传播速度较快,能够快速引燃整个燃烧室内的混合气,发动机输出功率稳定,初始条件变动对燃烧过程的影响较弱,因此在高频尺度范围内没有出现较明显的周期波动。同时,由于空气量较少,部分燃料不能完全燃烧,导致混合气成分会随着发动机运行时间而逐渐产生差异,从而导致持久性的大尺度周期波动出现。

(a)λ=1.0

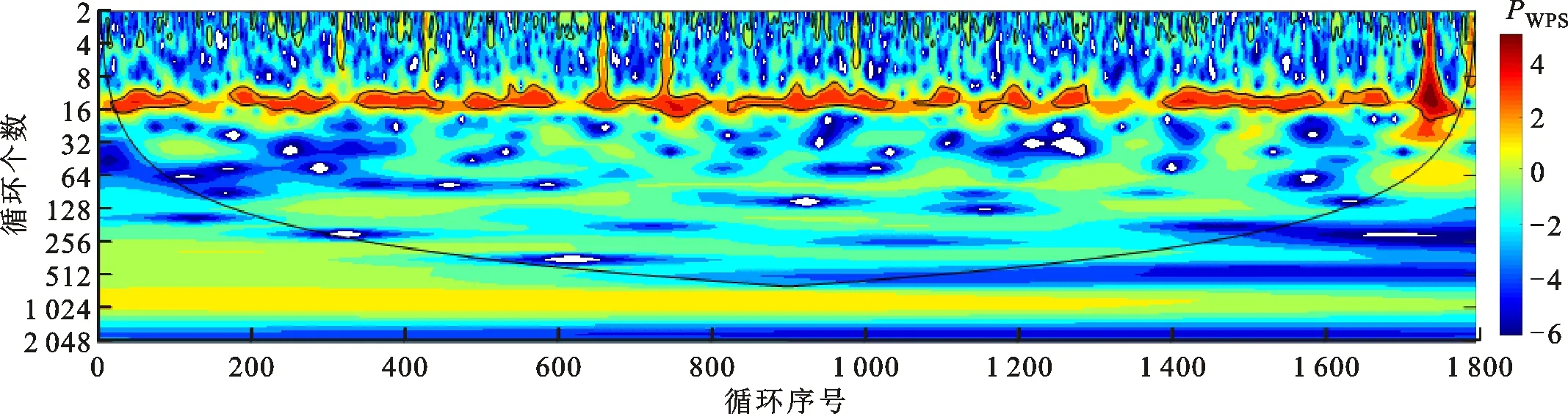
(b)λ=1.2

(c)λ=1.4

(d)λ=1.6

(e)λ=1.8

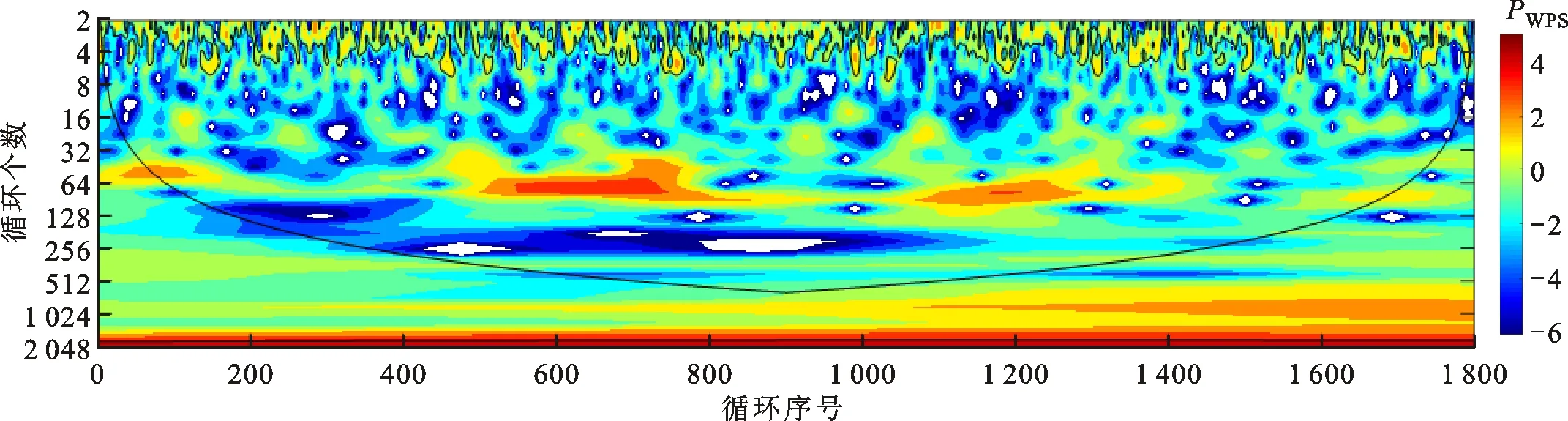
(f)λ=1.9图3 不同λ工况下的标准PWPSFig.3 Standard wavelet power spectrums under different λ conditions

当λ=1.2时,大尺度的周期波动消失,而在整个测得的1 800个燃烧循环内持续出现了尺度约为12个循环周期的周期性波动,同时在2到8个循环周期的更高频频带之间出现了少量间歇性的短暂周期性。当λ=1.4,1.6时,持久性的周期波动消失,高频频带范围内间歇性的短时周期性随着空气量的增多得到加强,间歇性所涉及的频带范围变得更宽。λ=1.6时,在2到24个循环周期的频带内,均有间歇性的短时周期波动出现。这些现象说明随着进入气缸内空气量的增多,燃烧不稳定性增强,高频频带范围内的波动增强,当前循环的燃烧过程受到了之前多个循环内燃烧状况的影响,使得邻近多个循环之间的关联性逐渐增强。这主要是由于空气量增多导致缸内温度降低,直接影响了初始火核的生成并延长了滞燃期,致使火焰传播速度变慢,循环变动加剧,当前循环的燃烧会直接影响后续多个循环,从而导致了燃烧不稳定性加剧。此时,需要提高点火能量,加速缸内混合气燃烧速率,才能降低天然气发动机燃烧不稳定性。

当λ=1.8时,在更高频范围内出现间歇性小尺度波动的概率增加,但波动的强度明显降低。这说明当前循环的燃烧过程更容易受到前一循环的影响,在8到16个循环周期的频带中,关联性变得相对较弱。当λ=1.9时,燃烧状况变得非常复杂,整个PWPS分散范围更广,在较大的尺度上再次出现了持久性的周期波动,但波动峰值未达到背景光谱95%的置信水平,高频尺度范围内的间歇性也变得非常嘈杂。在该工况下,已经接近了发动机运行的稀燃极限,燃烧可靠性大大降低,不完全燃烧和失火现象出现的概率急剧增加,从而导致发动机运行期间的燃烧状态极不稳定。

图4和图5分别给出了不同λ工况下1 800个燃烧循环的平均缸内压力和平均放热率变化曲线,结合发动机工作和燃烧过程特点,进一步验证小波分析结果。从图4中可以看出,随着λ增大,最高爆发压力pmax先增大后减小,λ=1.6时pmax达到最大值,而最高爆发压力对应的曲轴转角Φpmax在λ=1.9时提前较多。这主要是因为在试验过程中通过调节节气门开度来改变λ,当λ从化学计量比工况向稀燃工况变化时,一方面由于空气量增多可以改善燃烧质量,另一方面由于混合气总质量增多,两方面作用导致pmax增大,λ继续增加时,燃烧状况急剧恶化导致出现不完全燃烧和失火概率增加,pmax开始逐渐降低,此时燃烧速度降低,滞然期增长,燃烧过程错过了最佳燃烧相位,做功行程阶段混合气很难快速进入到大面积燃烧状态,而活塞下行导致缸内压力急剧下降,最终造成缸内压力很快达到峰值,即Φpmax提前。在图5中,随着λ增加混合气浓度降低,进而影响燃料的燃烧速度,导致放热率峰值逐渐降低,峰值所对应的曲轴转角呈延迟趋势。这与小波分析结果是一致的。

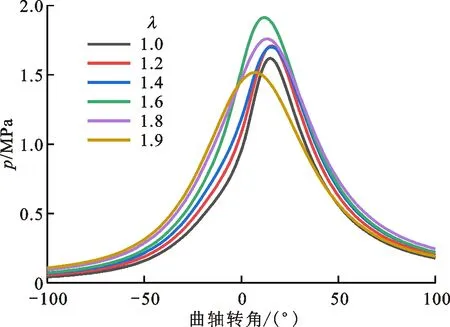
图4 不同λ工况下的缸内压力Fig.4 In-cylinder pressures under different λ conditions

图5 不同λ工况下的放热率Fig.5 Heat release rates under different λ conditions

3 多分辨率分析

离散小波变换将离散的时间序列信号分解到不同频带上,通过对特定频带范围内信号的分析,可以更加全面地揭示非线性系统的动力学特性,这一过程称为基于离散小波变换的多分辨率分析[22]。离散小波变换在实际应用过程中,将样本尺寸限制在了2j的整数倍上(j代表小波分解的最高水平),同时使用离散小波变换进行分解时需要经过二抽取过程,抽取结果可能导致原始时间序列信息丢失,经过分解得到的信号不能包含系统的完整信息。

极大重叠离散小波变换[23]克服了离散小波变换的缺点,可用来分析任意长度的时间序列,经过每一层小波分解得到的低频和细节信号与原始序列长度保持一致,同时极大重叠离散小波变换的细节和低频信号与零相位滤波器相关,可以更加容易地观察到原始时间序列的多尺度特征。将极大重叠离散小变换应用于天然气发动机燃烧不稳定性分析中,可得出不同尺度上时间序列的变异性,识别不同尺度上的燃烧特征,更加充分地揭示燃烧不稳定性产生的内在机理,这对于在发动机运行过程中的工况识别、燃烧边界参数的优化控制,进而降低燃烧不稳定性具有重要意义。

(5)

式中L表示滤波器的长度。尺度滤波器和小波滤波器之间存在如下式所示的正交镜像关系

(6)

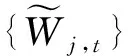
(7)

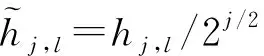
Lj=(2j-1)(L-1)+1

(8)

小波分解过程可用矩阵形式表示为

(9)

式中X={xn}为离散时间序列。在确定分解次数j0后,可根据极大重叠离散小波变换的各层小波系数和尺度系数重构出原始时间序列X

(10)

式中:Dj表示第j层的细节信号;Sj0表示第j0层的近似信号。将时间序列分解为1到j0层的细节信号和第j0层的近似信号(分解层数j代表不同的分辨率水平),高频细节信号表示原始时间序列在其相应频带范围内的波动信号,通过分析不同分辨率水平上的高频信号,可以进一步研究时间序列的多尺度特征。

为了揭示天然气发动机燃烧不稳定性的多尺度特征,将不同λ工况下pimep时间序列进行多分辨率分析。研究表明,采用不同小波函数对时间序列波动分析结果的影响不大[10],本文在分析过程中选取db8小波函数进行多分辨率分析,分解的级数可根据小波分析结果确定。从本文第2节PWPS分析中可以明显观察到,低频频带范围内的边缘效应更加严重,高频频带范围内影响锥区域更小,且随着进入气缸中空气量的增加,高频频带内出现了短时周期性的规律变化,说明空气量的变化导致邻近燃烧循环之间的关联性出现了不同程度的改变,而研究邻近燃烧循环之间的关联性对于分析燃烧不稳定性的动力学特性,实现边界参数的控制更具现实意义。

本文将不同λ工况下的pimep时间序列分解为3层,得到3个层次上的高频细节信号和低频平滑信号的近似,利用重构公式(10),将原始时间序列加性分解成3个高频细节信号{D1,D2,D3}和一个低频信号S3,定义如下式所示

(11)

式中:pimep时间序列的高频细节信号{D1,D2,D3}分别对应于2到4个循环周期频带、4到8个循环周期频带、8到16个循环周期频带内的局部波动信号;低频信号S3表示更大尺度范围内时间序列的整体波动特征。高频细节信号是原始时间序列在不同的循环周期频带范围内的局部波动信号,分析其相应的波动特征,可揭示信号的多尺度变化规律。

图6给出了λ=1.6工况下pimep时间序列的1到3层高频细节信号和第3层的低频分量。

表2给

(a)高频细节信号D1

(b)高频细节信号D2

(c)高频细节信号D3

(d)低频近似信号S3图6 λ=1.6工况下的高频细节信号{D1,D2,D3}和低频近似信号S3Fig.6 High-frequency detail signals {D1,D2,D3} and low-frequency signal S3 under λ=1.6 condition

表2 不同λ工况下细节分量的标准差Table 2 Standard deviations of detail signal component under different λ conditions

出了不同λ工况下pimep时间序列3个级别上细节分量的标准差。细节信号的标准差可以揭示pimep时间序列信号在不同尺度上波动特性,随着λ增加,3个频带中信号的标准差基本都出现了不同程度的上升,尤其当λ上升到1.8后,不同频带范围内信号的标准差急剧增加,表明随着进入气缸中空气量的增加,各个尺度上的波动明显增强,而空气量过多时,不完全燃烧和失火现象出现的频率急剧上升,造成天然气发动机燃烧稳定性恶化。当λ=1.2时高频细节信号D3相对于λ=1.4工况下高频细节信号D3的波动更加剧烈,这与该频带范围内出现的持久性周期振荡有关。

表3给出了不同λ工况下的pimep时间序列的循环变动系数PCCV,定量反映了天然气发动机燃烧不稳定性随λ的变化规律。随着λ增加PCCV增大,尤其是当λ达到1.8时,PCCV开始急剧上升,表明随着进入气缸内部空气量的增多,燃烧不稳定性开始增强,当空气量过多时,天然气发动机燃烧稳定性急剧恶化,各个工况下的PCCV与3个频带内细节信号的波动趋势一致。表4给出了细节分量的标准差{Std(Di),i=1,2,3}与PCCV的相关系数,相关系数均在0.95以上,具有足够高的相关性,表明随着λ增加天然气发动机燃烧不稳定性和3个频带范围内细节信号的波动特征具有较强相关性。

表3 不同λ工况下pimep的PCCVTable 3 PCCV of the pimep under different λ conditions

表4 细节分量的标准差和PCCV之间的相关系数Table 4 Correlation coefficients between PCCV and standard deviations of detail signal component

图7给出了所有λ工况下高频细节信号{D1,D2,D3}和低频信号S3对pimep时间序列的波动贡献率,从图中可以清晰地看出不同尺度上的分解分量对原始序列波动的贡献。在λ=1.0工况下,高频信号D1、D2和D3对pimep时间序列的波动贡献率分别为25.03%、13.06%和10.05%,而低频信号S3对燃烧不稳定性的贡献率达到了51.86%,因此当混合气浓度达到化学计量比时,低频信号S3对pimep时间序列的波动贡献较大。从本文第2节小波分析的结果显示,该工况下pimep时间序列在低频频带范围内出现了大尺度的持久性周期振荡,这些确定性成分的发现可以帮助开发有效的燃烧策略来降低低频信号的波动。在λ=1.2,1.4工况下,高频信号对燃烧不稳定性的贡献率均处于较高水平,特别是高频信号D1和D3的波动贡献率更大。在混合气更加稀薄时,高频信号D1对燃烧不稳定性的贡献率更大,尤其是λ=1.8,1.9工况下,高频信号D1对pimep时间序列的波动贡献率分别达到了48.29%和45.49%。这主要是因为稀燃工况下,火花塞附近天然气含量降低导致失火、不完全燃烧和爆震等非正常燃烧现象加剧,发动机燃烧稳定性恶化,然而稀燃条件下天然气发动机燃烧过程对初始条件的变化非常敏感[18],当前循环燃烧状况的微小变化都可能导致邻近燃烧循环之间的残余废气量、混合气成分和缸内空气动力学等状态出现较大变动,进而造成邻近循环之间的燃烧状况出现较大差异,因此导致了pimep时间序列在高频尺度空间内的波动更加明显,高频细节信号D1对pimep时间序列的波动贡献率更大。

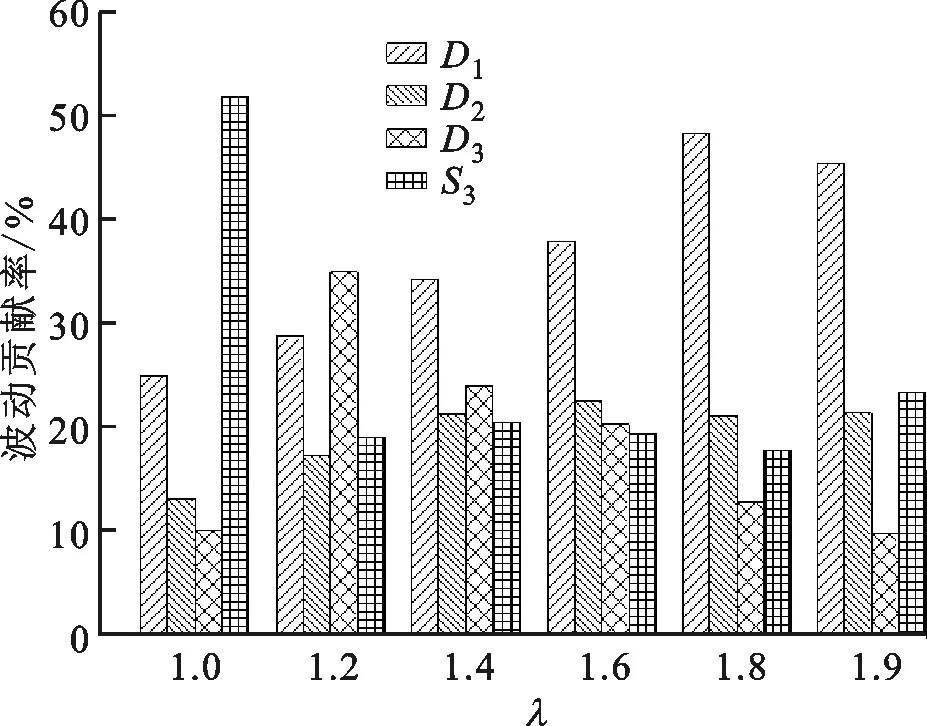
图7 高频细节信号{D1,D2,D3}和低频信号S3对pimep时间序列的波动贡献率Fig.7 Contributions of high-frequency detail signals {D1,D2,D3} and low-frequency signal S3 to pimep time series