实际气体效应对碳氢燃料点火延迟时间的影响

梁兴雨,廖寄语,朱仕皓,沈位,王昆

(天津大学内燃机燃烧学国家重点实验室,300072,天津)

由于储量大、能量密度高、稳定性好等方面的优点,碳氢燃料是现代动力机械的主要能源。常见热力设备如汽油机、柴油机、燃气轮机、蒸汽锅炉等,运行工况通常为高温(>1 000 K)高压(>3～5 MPa条件,此时碳氢燃料转化过程通常处于非理想的超临界状态。在该状态下,实际气体效应可能显著影响碳氢燃料的物化性质和基础燃烧特性。近年来,国内外学者对碳氢燃料开展了高压条件下的基础燃烧实验,包括测量组分浓度[1-2]、点火延迟时间[3-4]和层流燃烧速率[5-6]等。实验结果显示,碳氢燃料的负温度系数(NTC)区域随压力升高而变窄,并向高温方向偏移,其规律特点与常压条件差异较大。

高压对碳氢燃料基础燃烧特征的影响主要包括以下两方面。一方面,高压影响了燃料分子的基础化学反应动力学。压力变化使压力依赖型反应的反应速率出现剧烈变化,使关键中间产物的浓度出现较大改变,最终导致高压下的组分浓度、点火延迟时间和层流火焰燃烧速率呈现新特征[1,7]。另一方面,高压下实际气体效应显著,燃料分子的物性参数,包括密度、比热容、焓、导热率、黏度、二元扩散系数等,逐渐偏离理想气体假设,进而导致燃烧反应体系中的基元反应速率、中间产物分布等发生改变,最终改变燃料的宏观燃烧特性,包括燃烧终产物类型、点火延迟时间、层流火焰速率等。压力依赖型化学基元反应的构建可由第一性原理计算和实验测量获得,通常在化学反应动力学机理的构建过程考虑。因此,本文主要探究实际气体效应的影响(以点火延迟时间的计算为对象)。

目前,已有少量研究考虑了实际气体效应对碳氢燃料基础燃烧特征的影响。Kogekar等测量了正十二烷在4～8 MPa条件下的点火延迟时间,并考察了Redlich-Kwong状态方程[8]对点火延迟时间的影响[9]。Gao等探究了实际气体效应对甲醇/氧气/水火焰的影响,发现25 MPa下的产物分布、层流火焰速率、火焰位置等与理想气体假设下的差异较大[10]。为了反映实际气体效应对燃料物性参数的影响,许多研究者提出了修正模型。在输运参数方面,Chung等提出了对黏度和导热率的压力修正模型[11],而Takahashi提出了二元扩散系数的高压模型[12]。在物性参数方面,不同学者基于不同假设提出了各种实际气体状态方程,包括van der Waals状态方程、Redlich-Kwong方程[8]、Peng-Robinson方程[13]等。这些研究表明,实际气体效应对碳氢燃料的基础燃烧反应特性存在较为显著的影响。当前对该效应的研究主要集中在小分子燃料(如甲烷、氢气、甲醇、二甲醚等),对大分子碳氢燃料的研究相对稀少。

此外,当前主流的化学动力学模型软件如ChemKin-Pro[14],出于编程的简易性和计算成本考虑,大多采用理想气体状态方程的假设,因而在高压尤其是超临界压力条件下可能导致较大误差,不能准确反映碳氢燃料的实际燃烧特征。因此,本文基于开源化学反应动力学计算软件Cantera,构建考虑实际气体效应的基础燃烧特性计算平台,以研究实际气体效应对不同碳氢燃料点火延迟时间的影响。具体地:首先,在Cantera软件中植入实际气体状态方程,包括van der Waals方程和Peng-Robinson方程,进而考察由以上实际气体状态方程推导而来的热力学参数(包括比热容、焓、熵和吉布斯自由能等)和描述实际气体效应的特征量(包括逸度系数、压缩因子和活度系数等)的变化;其次,将实际气体效应下获取的物性参数的实验值和计算值进行对比,验证模型的准确性;然后,利用官能团贡献法[15-16]估算反应体系中化学物质的临界性质,确定其在实际气体状态方程中的参数;最后,以丙烷、正庚烷和正十二烷代表3类不同分子链长度碳氢燃料,考察实际气体效应对点火延时时间的影响。

1 理论方法

1.1 气体状态方程

气体状态方程描述了物质状态参量之间的关系。对于温度、压力和组分已知的混合物,密度可直接由气体状态方程确定,其他物性(如焓、熵、吉布斯自由能等)也间接受状态方程的影响。在各类不同形式的状态方程中,得到广泛应用的状态方程(EOS)主要包括理想气体状态方程、van der Waals状态方程(vdW方程)、Redlich-Kwong状态方程[8](R-K方程)、Peng-Robinson状态方程[13](P-R方程),即本文考虑的4类状态方程。它们可统称为立方型状态方程,并具有统一的表达形式

(1)

式中:p代表压力;R代表通用气体常数;T代表温度;v代表摩尔体积,a、b代表状态方程参数,与物质的临界温度Tc、临界压力pc有关;u、w代表系数;α(Tr)代表与对比温度Tr=T/Tc有关的函数。4类状态方程中参数的取值如表1所示。其中,P-R方程中κ=0.374 6+1.542 26ω-0.269 92ω2,代表与偏心因子ω有关的修正系数。

对于混合物,其方程参数amix和bmix为

(2)

(3)

(4)

式中:下标i和j分别代表组分i和组分j;X代表摩尔分数。焓、熵直接由分离函数[17]求得

(5)

(6)

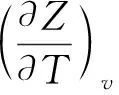
表1 统一表达形式下的4种气体状态方程参数取值Table 1 Parameter values of four equations of state

求得剩余焓、剩余熵后,可按照相应的定义导出其他剩余性质,如比定压热容(Cp)、摩尔比吉布斯自由能(g′)、摩尔比亥姆霍兹自由能(f)等。本文对Cantera软件进行了二次开发,编写了代码,基于vdW方程、R-K方程、P-R方程推算剩余性质,其表达式如表2所示。

表2 不同实际气体状态方程下剩余性质的表达式Table 2 Residual properties evaluated by different EOS

1.2 反映气体非理想性的特征量

实际气体效应受压力、温度、组分等多种因素影响。为均一化地体现气体的非理想性,存在不同的评判标准和相关标准。本小节主要介绍其中常见的压缩因子、逸度系数、活度系数,并描述它们在状态方程中的表达形式。

压缩因子Z反映实际气体与理想气体在摩尔体积上的差异,计算公式为

(7)

同样地,逸度f表征实际气体的有效压力,其与压力的比值为逸度系数φ。逸度系数反映实际气体与理想气体在压力上的差异,计算公式为

(8)

在化学反应动力学中,实际气体的物质的量浓度[X]用活跃浓度 [C]代替,二者比值为活度系数γ

(9)

理想气体的压缩因子、逸度系数、活度系数均恒为1。实际气体与理想气体的差值越大,则实际气体效应越明显。

对于任意基元反应i,其过程变化率qi修正为

(10)

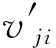
(11)

(12)

式中fj,partial代表组分j用逸度代替压力的分压。由此可见,实际气体效应从基元反应层面直接影响化学反应的边界条件,可能导致高压燃烧反应特征量偏离理想气体假设。依据定义,组分j的逸度系数φj、混合物整体(或纯单质)的逸度系数φ、组分j的活度系数γj,由

(13)

(14)

g′=h-Ts

(15)

(16)

(17)

联立气体状态方程求得。式中:ntot和nj分别代表总物质的量和组分j的物质的量;μj和μj,0分别代表将组分j视为实际气体和理想气体时的化学势。式(16)表示在压力、温度、其他物质的物质的量不变的前提下,对总吉布斯能的偏导数。

以P-R方程为例,推导实际气体的逸度系数φ。根据Segura和Wisnaik的研究结果[18],逸度系数φ的表达式等价于

(18)

将P-R方程的表达式代入式(18),消去压力,再进行积分,得到

(19)

这些状态参量的表达式、由实际气体状态方程推导而来的逸度系数和活度系数均已在Cantera中实现。

1.3 物质与自由基临界性质的估算

由式(1)可见,状态方程中的参数a、b须在模拟计算前确定,而该参数由临界性质(对P-R方程还有偏心因子)决定,因此须获取反应体系中化学物质(包括稳定化合物和自由基)的临界性质。对稳定物质(即分子结构无孤对电子,如甲烷CH4、乙烷C2H6分子等),其临界性质和偏心因子可由实验测得,但对化学反应过程存留时间较短的自由基(即分子结构包括孤对电子,如甲基CH3·、乙基C2H5·等),只能通过估算方式获取。在化学结构已知的情况下,官能团贡献法一般被认为是常用且可靠的估算方法。此类方法的核心假设物性参数(沸点、熔点、临界温度、临界压力、临界体积、偏心因子等)与化学官能团的种类和数量相关。根据官能团贡献法,首先须将物质拆分成若干官能团,然后统计各官能团的出现频次,最后对所有官能团的出现频次与对应的贡献值之积进行累加以获得估算值。不同物性参数的估算值与官能团的函数关系不同。本文采用Joback法[15]和Constantinou法[16]分别计算稳定化合物和自由基的临界性质和偏心因子,估算公式为

(20)

(21)

(22)

(23)

式中:Tb、Tc、pc、ω分别代表物质的沸点、临界温度、临界压力和偏心因子;下标i和j代表官能团的编号;Ni和Nj代表物质中官能团i和官能团j的总数;Cprop,i代表官能团i对性质prop(包括沸点、临界压力、临界温度和偏心因子)的贡献值;NA表示物质的原子总数;k1、k2、k3、K是无量纲通用常数,分别取0.408 5、0.505 0、1.150 7、1。

1.4 反应器模型与化学动力学模型

本文研究所有的动力学模拟计算,均在开源化学动力学计算平台Cantera完成,该平台基于C++编程语言构建,具有面向对象、易于拓展、计算成本低和自带跨语言接口等优点。在Cantera自带的理想气体模型和Kogekar等实现的R-K状态方程[9]的基础上,本文研究进一步将VdW方程和P-R方程以及相应的状态参量表达式植入到该平台,并成功应用于化学动力学计算。本文研究采用零维均质定容绝热反应器模型计算燃料的点火延迟时间(IDT),其控制方程为

(24)

(25)

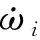
表3 用于计算点火延迟时间的反应动力学模型Table 3 Reaction kinetic mechanisms for IDT calculations

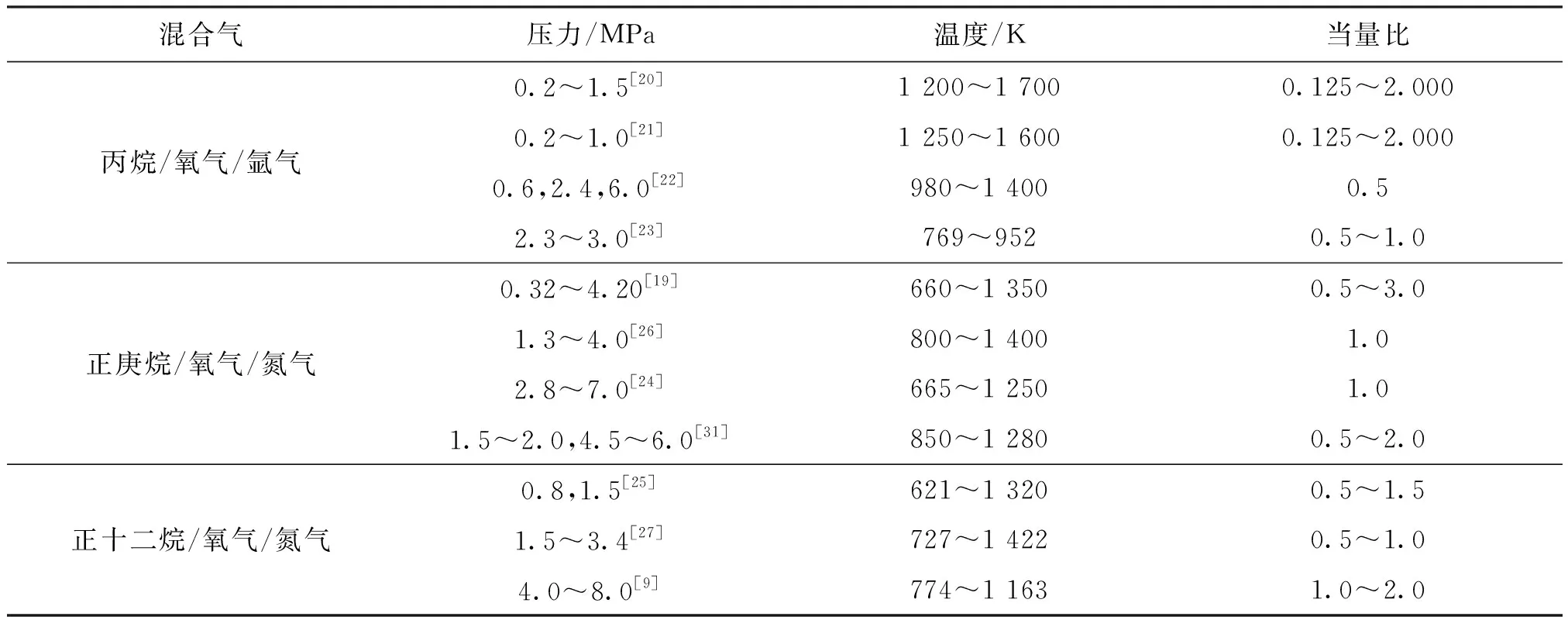
表4 用于验证实际气体效应的点火延迟时间实验数据Table 4 Experimental dataset for IDT validations

2 结果与讨论

2.1 Cantera动力学计算结果的验证

首先,为验证Cantera的可靠性,将其计算结果与商用化学动力学计算软件Ansys ChemKin-Pro[14]的计算结果进行对比,如图1所示。实验条件为正庚烷/空气,当量比φ=1,压力p=0.65 MPa。可以看出,二者计算结果一致性较好。

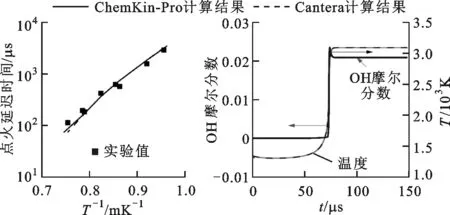
(a)点火延迟时间[19] (b)混合气初始温度为1 340 K时的时间历程图1 Cantera和ChemKin-Pro计算结果的对比Fig.1 Comparison between Cantera and ChemKin-Pro for IDT calculations

2.2 官能团贡献法的可靠性验证

为验证官能团贡献法的可靠性,选取若干种具有不同官能团的物质,将临界性质及偏心因子的实验值与估算值进行对比,结果如表5所示。实验值来自NIST数据库[32]和文献[33]。可以看出,由Joback法和Constantinou法获得的临界性质和偏心因子的相对误差均控制在15%内,可靠性较好。因此,后续点火延迟时间的计算流程中首先采用该方法预估化学物质和自由基的状态方程参数。

表5 利用官能团贡献法获得的部分化学物质的物性参数估算值与实验值对比Table 5 Validation of group additivity method against experimental data for some physical properties

2.3 物性参数验证

2.3.1 单组分物性参数 为验证van der Waals和Peng-Robinson方程植入Cantera后计算的可靠性,选择正十二烷、氧气、氮气分别代表反应体系中的燃料、氧化剂、稀释剂,选择0.1、1、10、30 MPa共4个压力点,在100～1 500 K的温度区间,计算密度ρ、比定压热容Cp和压缩因子Z。图2～4为这些参数的计算值与NIST数据库实验值[32]的对比。

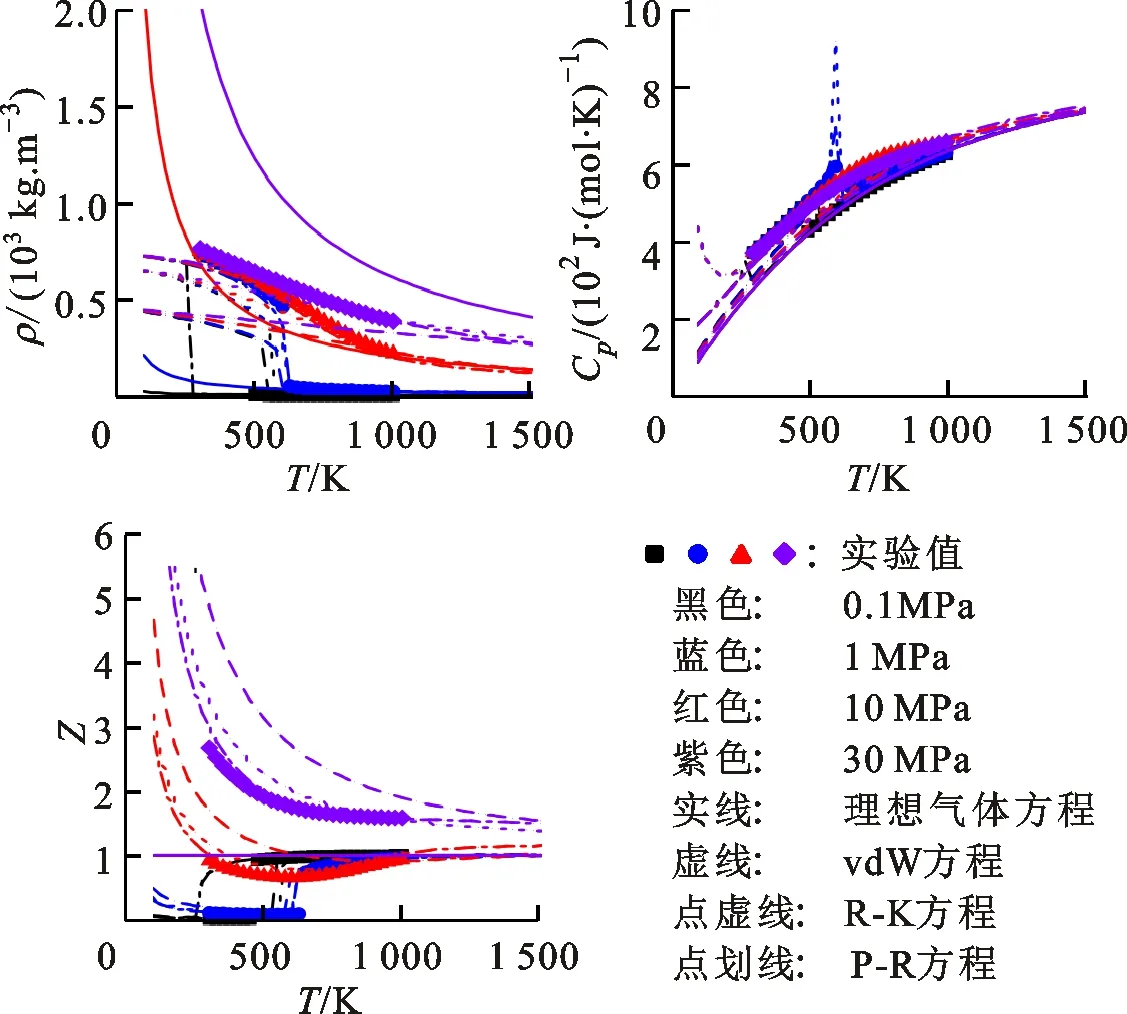
图2 正十二烷的物性对照Fig.2 Validation of physical properties for n-dodecane

图3 氧气的物性对照Fig.3 Validation of physical properties for oxygen

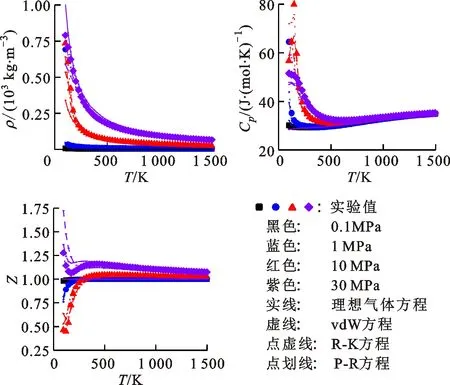
图4 氮气的物性对照Fig.4 Validation of physical properties for nitrogen

图2表明,高压下正十二烷的密度、比定压热容和压缩因子均与大气压下有较大差异。同时,利用理想气体状态方程计算得到的密度、比定压热容、压缩因子也与实验值偏离较大,已不能合理描述气体特征。在实际气体状态方程中,3种方程均能正确捕捉到物性的变化趋势,且R-K方程和P-R方程能更好地描述高压情况下的气体特征。在较低压力(300～500 K)时,实际气体状态方程对正十二烷的密度预测有一定差异,这是由于正十二烷处于液态及向气态转变的相变点附近(正十二烷的常压沸点为489 K),用气体状态方程较难得到准确结果。

此外,在图2c中,压力为0.1 MPa时气体的非理想性较弱,可视为理想气体处理,而在高压条件下,气体的非理想性较强,受温度的影响较大。具体而言:在100～600 K时,气体的非理想性非常强,且随着温度的升高而降低;在600～1 000 K,即大部分碳氢燃料的NTC区域时,气体的非理想性仍较强,将对点火延迟时间造成较大影响;在高温区(>1 000 K)时,气体的非理想性减弱,进而导致实际气体修正对滞燃期的影响减弱。氧气和氮气的非理想性即使在非常高的压力下也不强,理想气体状态方程也能在研究的温度范围内(600～1 500 K)很好地描述它们的物性,因此它们可按理想气体处理。总体而言:高压条件下,大分子碳氢燃料在NTC区域的非理想性较强,温度继续升高或降低都会导致非理想性减弱;氧气和氮气受压力的影响较弱,理想气体状态方程也能很好地描述其性质。

2.3.2 混合组分物性参数 本小节进一步探究了温度和当量比对碳氢燃料混合物非理想性的影响,工况见表6。计算的混合气压缩因子Z、逸度系数φ和活度系数γ见图5和图6。

表6 混合气的对比条件Table 6 Gas mixture for validation

图5 正十二烷/空气混合物在不同当量比和温度下的物性变化Fig.5 Physical properties of n-dodecane/air mixture under varying equivalence ratio and temperature

在图5中,燃料的活度系数在高压条件下明显偏离理想气体表现,3种实际气体方程对应的结果有一定差异,但都能反映出其非理想性。随着当量比的增加,活度系数略有降低,压缩因子和逸度系数略有增加;随着温度的增加,燃料的活度系数有明显增加,在NTC区域(800～1 000 K)达到较高水平,将对这一温度区间下的点火延迟时间产生较大影响。非理想情况下,氧气和氮气的活度系数、压缩因子和逸度系数与理想气体接近(均在1.02～1.04之间),且对当量比、温度、状态方程均不敏感,其实际气体效应可忽略不计。图6表明,将稀释气替换为氩气时,规律差异不大,只有燃料的实际气体效应对温度、当量比、状态方程敏感,氧气和氩气仍可视为理想气体。燃料的活度系数随着温度的升高而增加,在900～1 100 K时达到较高水平,反映出较强的非理想性。该规律与2.2小节结论较为一致。

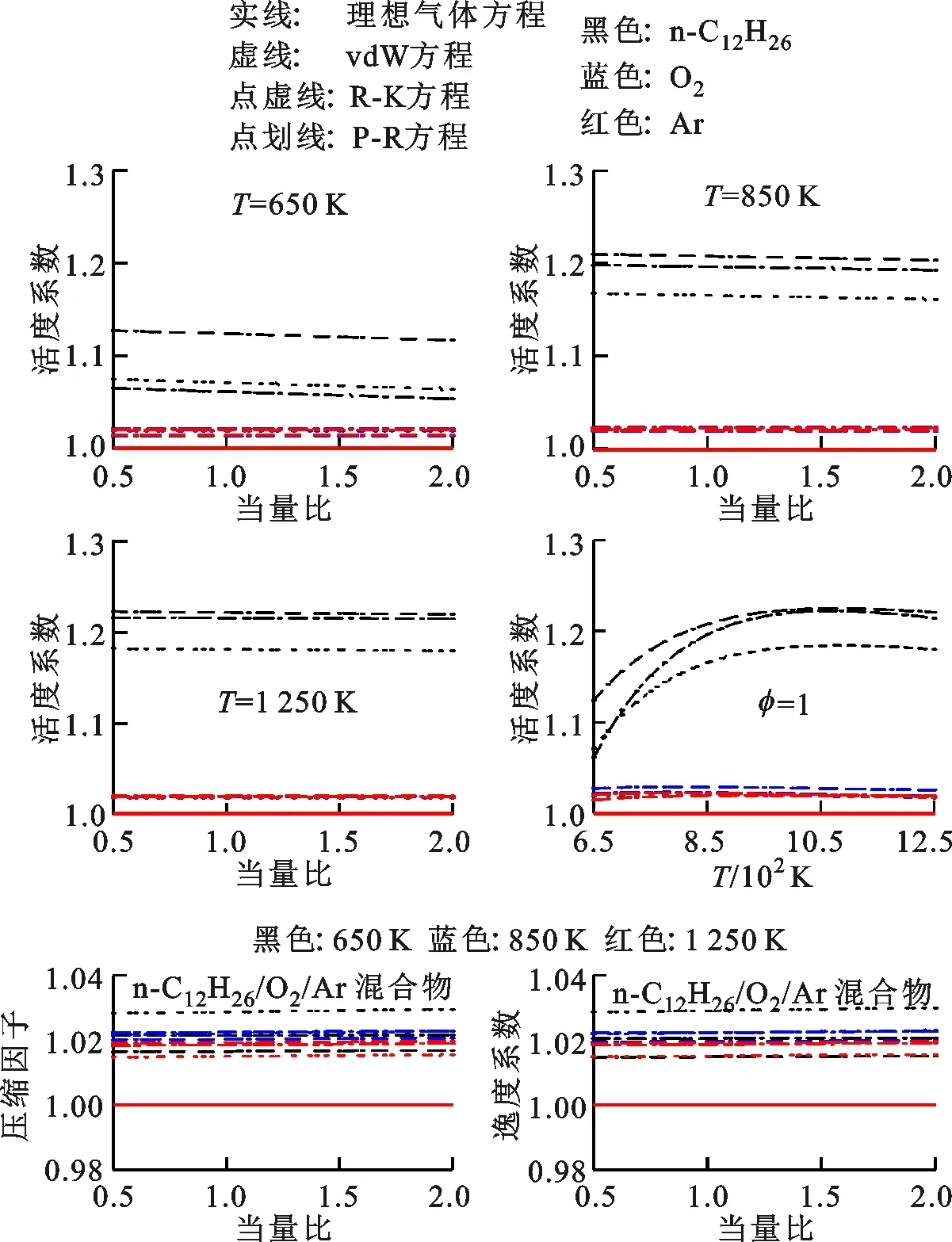
图6 正十二烷/氧气/氩气混合物在不同当量比和温度下的物性变化Fig.6 Physical properties of n-dodecane/oxygen/argon mixture under varying equivalence ratio and temperature

2.4 点火延迟时间数据的验证与分析

为分析实际气体效应对点火延迟时间的影响程度,定义由实际气体效应引起的非理想偏差ε为实际气体和理想气体假设下点火延迟时间的差值占理想气体假设下点火延迟时间的百分比,即

(26)

式中τideal和τreal分别表示按理想气体假设和采用实际气体状态方程获得的点火延迟时间。

正庚烷、正十二烷和丙烷在高压下点火延迟时间的实验值与模拟值如图7～10所示。

(a)不同状态方程算得的点火延迟时间与实验值[19,24,26,31]的对比 (b)P-R方程不同压力下实际气体效应引起的点火延迟时间非理想性偏差图7 正庚烷的点火延迟时间验证Fig.7 Validation of IDT for n-heptane/air mixture

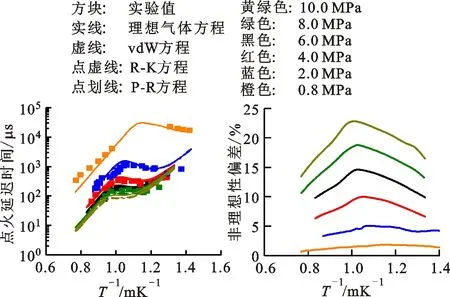
(a)不同状态方程算得的点火延迟时间与实验值[8,25,27]的对比 (b)P-R方程不同压力下实际气体效应引起的点火延迟时间非理想性偏差图8 正十二烷的点火延迟时间验证Fig.8 Validation of IDT for n-dodecane/air mixture

图9 不同气体状态方程下正十二烷的高压点火延迟时间Fig.9 High-pressure ignition delay time of n-dodecane/air mixture from different EOS

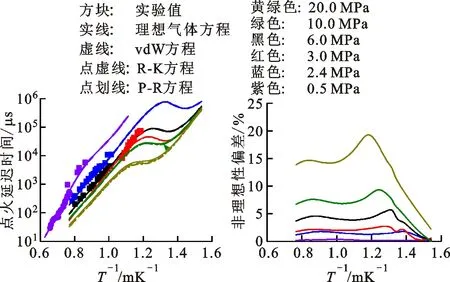
(a)不同状态方程算得的点火延迟时间与实验值[20-23]的对比 (b)P-R方程不同压力下实际气体效应引起的点火延迟时间非理想性偏差图10 丙烷的点火延迟时间验证Fig.10 Validation of IDT for propane/oxygen/argon mixture

从图7a可以看出:模拟值与实验值的一致性总体良好;在高压、800～1 000 K(NTC区域)条件下,点火延迟时间模拟值略大于实验值,引入实际气体修正后,点火延迟时间降低,接近实验值;3种实际气体状态方程均能提升实验值和模拟值的一致性,且相互间差异不大。从图7b可以看出,由实际气体效应引起的非理想性偏差与温度、压力之间存在较强关联。具体地:同一温度下,随着压力的升高,实际气体效应显著增强,偏差也随之增加。当压力高于燃料临界压力(即燃料进入超临界态)时,非理想性偏差可达到8%～15%;同一压力下,非理想性偏差在燃料的NTC区域达到峰值。这是由于燃料在NTC区域时的非理想性最强,而温度升高时,气体的非理想性减弱。随着压力的增加,燃料的NTC区域变窄且向高温方向移动,偏差的峰值点也向高温方向移动。从图8a可以看出,正十二烷的结果与正庚烷相似,动力学模型的点火延迟时间模拟值与实验值的一致性良好,3种实际气体状态方程对应的计算结果差别不大。非理想性偏差方面,其随温度、压力的变化情况与正庚烷也相似,但同一压力下,偏差的峰值点出现在更高的温度,这是由于碳链的延长使NTC区域向高温方向移动。

此外,同一压力下,正十二烷的非理想性偏差比正庚烷大,这可能是因为正十二烷的临界压力更低(1.80 MPa),对比压力pr更高。对于碳链更长、临界压力更低的碳氢燃料(如正十六烷和异十六烷,临界压力分别为1.40 MPa和1.57 MPa[32]),它们在高压下的实际气体效应更显著,点火延迟时间受压力的影响可能更明显。因此,计算大分子碳氢燃料高压下的点火延迟时间时,须考虑实际气体效应,否则可能会造成较大误差。

图9对比了不同气体状态方程假设下正十二烷在4.0和6.0 MPa的点火延迟时间。可以看出,考虑实际气体效应后的点火延迟时间预测值比理想气体假设下的预测值更接近实验值,尤其是在NTC区域,二者的差异较为明显。事实上,要准确描述高压或超临界压力条件下碳氢燃料的非理想燃烧反应特征,除考虑实际气体效应外,还须要考虑以下两方面的因素:①准确、合理的化学反应动力学模型,尤其是压力依赖型基元反应,其反应速率不仅与温度相关,同时也是压力的函数,须要恰当处理;②高质量、可靠的实验测量数据。通常在高压、超临界压力条件下,基础燃烧反应动力学实验的挑战更大,导致数据误差也较大。最重要的是,当前高压或超临界压力条件下的基础实验数据非常匮乏。将这些方面综合考虑,方能对高压或超临界压力条件下碳氢燃料的燃烧化学反应特征进行准确描述。

图10对比了碳链较短的碳氢燃料——丙烷的点火延迟时间受实际气体效应的影响。可以看出,虽然常压下丙烷对应的NTC区域的温度比正庚烷和正十二烷的低(700～750 K),但非理想性偏差的变化规律与两种碳链较长的碳氢燃料类似。此外,同一压力下,丙烷的非理想性偏差比正庚烷和正十二烷的低,这可能是因为丙烷的临界压力比较高(4.25 MPa)。

本小节分析表明:实际气体效应对碳氢燃料的点火延迟时间的影响存在共性:非理想性偏差随压力的升高而增加,而且可能与燃料的临界压力有关;非理想性总在NTC区域达到峰值,向高温或低温方向移动都会使其降低。

3 结 论

本文考察了高压条件下实际气体效应对碳氢燃料点火延迟时间的影响。首先,对开源化学反应动力学模拟平台Cantera进行二次开发,植入van der Waals、Peng-Robinson状态方程,构建具有实际气体修正的反应器模型;然后,选取代表性燃烧化学反应体系,研究不同的压力、温度、当量比条件下实际气体效应对物理化学性质的影响;最后,开展了实际气体和理想气体假设下燃料的点火延迟时间的燃烧反应动力学仿真。本文结论如下。

(1)高压条件下实际气体效应对点火延时时间影响显著,须考虑实际气体效应以获得准确的仿真结果。

(2)实际气体效应引起的点火延迟时间非理想性偏差与温度和压力具有较强关联:压力越高,非理想性偏差越高;随着温度的升高,非理想性偏差先增大后减小,并在NTC区域温度达到峰值。

(3)非理想性偏差也与对比压力、碳氢分子的碳链长度、临界压力等相关,长碳链、低临界压力燃料的非理想性偏差一般更显著。