变负载柔性机械臂复合学习控制

2022-02-14曹怀磊邓文翔姚建勇

西安交通大学学报 2022年1期

曹怀磊,邓文翔,姚建勇

(南京理工大学机械工程学院,210094,南京)

机械臂广泛应用于工业[1]、航空航天[2]和医疗[3]等领域。传统的机械臂刚性较强,易实现精确控制,但也存在负载自重比小、能耗高等缺点,难以满足轻量、高速、低能耗等应用需求。

柔性连杆机械臂的臂杆采用轻质材料制成,响应快、能耗低、操作灵活、工作效率高,逐渐在医疗、高精密制造业、太空探索等领域凸显出其优越性[4]。但是,由于刚度的降低,柔性连杆机械臂在运动时会发生弹性形变,系统非线性变得更复杂,同时负载随着任务变化而变化,存在不确定性,给运动控制策略设计带来了非常大的挑战。因此,柔性机械臂的高精度运动控制成为了近些年来的研究热点[5]。

为了提高柔性连杆机器臂的运动轨迹跟踪控制性能,目前已经有多种控制方法被提出,如自适应控制[6-7]、奇异摄动控制[8-9]、迭代学习控制[10-11]、自抗扰控制[12]。这些控制方法有效的处理了柔性机械臂系统参数不确定性,实现了良好的轨迹跟踪,但并未对连杆柔性产生的非线性不确定性作出针对性处理,也未考虑末端负载变化。文献[13]针对负载不确定的柔性机械臂位置控制问题提出了一种自适应自抗扰控制方法,将系统分为快慢子系统,在快时标系统中利用线性二次型控制器处理连杆柔性的影响,在慢时标系统中采用迭代最小二乘法估计负载的质量,作为补偿项加入到自抗扰控制器中,但该方法模型结构复杂,设计过程烦琐,控制参数过多难以调节。

由于具有强大的逼近非线性函数能力,神经网络在柔性机械臂控制被广泛使用[14]。文献[15]将模糊神经和PD控制相结合,用于变负载条件下的柔性机械臂运动控制。Rahmani等采用基于线性内参数的神经网络来逼近和消除由连杆柔性引起的不确定性[16]。但是,神经网络在实际应用时仍存在一些典型问题,如最佳学习参数难以确定[17]、运行初始阶段逼近误差较大[18]等。在变负载柔性机械臂系统中,除了连杆柔性引起的不确定性,还包括负载变化、非线性摩擦等效应的集中干扰,仅靠神经网络很难同时处理这些问题。

基于这些考虑,针对变负载柔性连杆机械臂的运动控制问题,本文提出了一种复合学习控制(NNDORC)方法。针对由连杆柔性引起的非线性不确定性,利用径向基神经网络(RBFNN)进行逼近和消除;针对负载变化、非线性摩擦、RBFNN逼近误差等效应的集中干扰,构造干扰观测器(DOB)进行实时估计;将两者用于控制器的前馈补偿设计以提升系统跟踪性能。此外,设计鲁棒反馈控制律保证系统的稳定性。通过Lyapunov稳定性理论证明了所提控制方法可保证跟踪误差的有界性和闭环系统的稳定性。基于柔性机械臂平台的对比实验验证了本文所提方法的有效性和优越性。

1 动力学模型

考虑末端带有质量可变负载的单杆柔性机械臂的运动控制,将其视为Euler-Bernoulli梁[19],物理模型如图1所示。图中:XOY为惯性坐标系,xOy为固连在机械臂上的浮动坐标系;g为重力加速度;长为L的机械臂一端固连在驱动关节上,另一端为自由端且带有可视为质点的负载;负载质量m不确定,其变化范围为0～1倍的臂重;ρ为柔性臂的线密度(即单位长度的质量);E为弹性模量,I为截面惯性矩,EI为机械臂的抗弯刚度;Jh为旋转关节的转动惯量。

旋转关节由伺服电机产生的力矩τ驱动,柔性臂夹持在关节上随之运动,θ(t)为柔性机械臂的旋转角度,δ(x,t)为在运动过程中由于臂杆柔性在x处产生的弹性变形。

根据假设模态法,在运动过程中t时刻,连杆在x处的变形可以描述为[20]

(1)

式中:φi(x)表示第i阶振型函数;qi(t)表示对应的模态坐标。前几阶模态足够描述机械臂的变形,剩余模态对系统的影响可以忽略不计。本文考虑系统前2阶模态,即

(2)

振型函数φi(s)表达式为

φi(x)=ai[cosh(βix)-cos(βix)-

(3)

式中βi为频率方程的特征根,频率方程为

1+cosh(βL)cos(βL)

(4)

αi为归一化函数求出的非0常数,归一化函数为[21]

(5)

结合假设模态法和Lagrange法[22-23],柔性连杆机械臂动力学方程可以写为

(6)

式中:M为质量正定矩阵;B为阻尼矩阵;K为刚度矩阵;f为科氏力和向心力矩阵;G为重力矩阵;θ和q=[q1q2]T分别代表机械臂的刚性转角和弹性变形的模态坐标;Δ为系统非线性摩擦、建模误差等综合项;由文献[24]可知,τ=kuu,其中ku为力矩放大系数,u为控制输入。

为了便于分析系统的非线性项和控制器设计,将动力学方程式(6)重新写为

(7)

(8)

式(7)代表系统的刚性部分,主要表征运动中连杆的角度变化,式(8)代表系统的柔性部分,主要表征运动中连杆的弹性变形。两式互相耦合,式(8)可以重新写为

(9)

将式(9)代入式(7),可以得到新的动力学方程

(10)

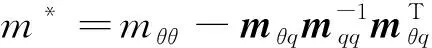
式(10)从形式上看类似于刚性机械臂的运动学方程,但其中m*是综合了刚性和柔性项的等效质量,而h则代表了由于系统柔性部分带来的系统非线性不确定函数。

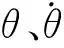
(11)

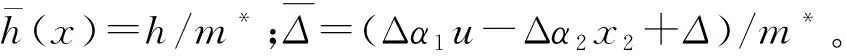
为便于控制器设计,做出如下合理假设。

假设1系统期望角度信号x1d(t)二阶连续可微且其各阶导数均有界。

2 控制器设计

本文的控制目标是在柔性机械臂末端负载质量变化的情况下,能够克服系统非线性不确定性和集中干扰,使系统状态x1能够跟踪到期望角度信号x1d,控制器结构如图2所示。

图2 NNDORC控制器结构Fig.2 Structure of NNDORC controller

定义误差变量

(12)

式中:z1为角度跟踪误差;x2d为状态x2的虚拟控制律;z2为两者之间的偏差。

设计虚拟控制律x2d为

(13)

式中k1为反馈增益系数,k1>0。

根据式(11)～(13),可以得到误差动态方程

(14)

2.1 RBF神经网络设计

RBF神经网络是一种3层前项网络,可以任意逼近未知非线性函数,其输入层到隐含层的映射是非线性的,而隐含层到输出层的映射是线性的,因此可以加快学习速率并避免局部极小值问题[25]。RBFNN结构如图3所示。

图3 RBFNN结构Fig.3 Structure of RBFNN

(15)

成立。式中:ω=[ω1ω2ω3ω4ω5]T代表神经网络最优权值;ε为逼近误差;R(X)=[R1R2R3R4R5]T为神经网络基函数,Rj表达式为

(16)

其中,Cj=[cj1cj2cj3]T表示隐含层第j个节点的中心矢量,bj为第j个节点的基宽度参数,bj>0。

将式(15)代入式(11),x2的动态方程变化为

(17)

同时,z2的动态方程可以写为

(18)

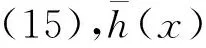
(19)

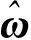
设计神经网络权值更新律为

(20)

式中γ和α是设计参数,γ>0,σ>0。

(21)

2.2 非线性干扰观测器设计

为了处理总干扰d,设计一种非线性干扰观测器

(22)

(23)

进而可以得到

(24)

2.3 复合控制律设计

根据2.1、2.2小节设计的神经网络和干扰观测器,结合式(19)(20)(22),最终的复合控制律设计为

(25)

式中k2为反馈增益系数,k2>0。

根据式(18)(25),误差动态方程可以重新写为

(26)

3 稳定性分析

理论1对于式(11)描述的柔性机械臂系统,基于RBFNN(式(19)(20))和DOB(式(22))所设计的控制器NNDORC(式(25))可以保证闭环系统中所有信号有界,实现系统有界稳定。

证明定义Lyapunov函数

V(t)=V1+V2+V3+V4

(27)

由式(21)(24)(26)可以得到

(28)

(29)

(30)

(31)

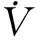
(32)

利用简单的数学关系,可以得到

(33)

式中:‖R‖2≤Θ;ν1和ν2为任意正数。

(34)

定义

(35)

选取合适的σ、v1、v2、kd,使得k3>0,k4>0,则

(36)

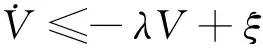
(37)

式中λ=min[2k1,2k2,2γk3,2k4]。

根据V(t)的定义以及有界性定理,可以得到

(38)

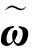
4 实验验证与分析

4.1 柔性机械臂实验平台介绍

实验平台由机械系统和测控系统两部分组成。机械系统如图4a所示,主要包括支座、直流伺服电机、旋转关节和柔性机械臂,伺服电机和旋转关节通过联轴器连接,柔性机械臂直接固连在旋转关节上,同时配有角度编码器。测控系统如图4b所示,主要包括工控机、PCI-1716A/D转换板卡、PCI-1723D/A转换板卡、光电编码器数据采集卡、显示器等,控制器程序在下位机中由C++代码编写,并在上位机中构建可视化监控软件。

(a)机械系统

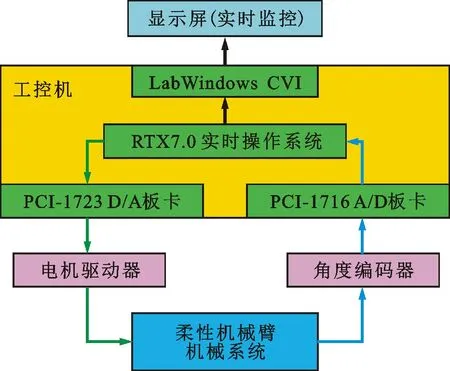
(b)测控系统图4 柔性机械臂实验平台Fig.4 Flexible manipulator experiment platform

实验台各参数如下:Jh=0.3 kg·m2,柔性机械臂长L=0.5 m,宽度b=0.049 8 m,厚度h=0.004 m,E=2×1011N/m2,线密度ρ=1.52 kg/m,重力加速度g取9.8 m/s2,负载质量m变化范围为0～0.5 kg。系统中其他参数均可由这些参数计算得出。

实验采样间隔为0.5 ms,角度信号由编码器采集得到,速度信号由高精度角度信号向后差分得到,同时采用截止频率为50 Hz的二阶Butterworth滤波器来减少速度信号中的测量噪声。

4.2 实验结果及分析

为验证所设计控制器的有效性和优越性,选取3种控制器进行对比实验

(1)本文提出的复合学习控制器(NNDORC)。系统参数的名义值选择为α1n=3.22,α2n=1.10,α3n=2.51;反馈增益k1=k2=50;RBFNN权值参数γ=50,σ=0.01,b1～b5均为5.0,C1=[0.20.62.5]T,C2=[0.10.31.25]T,C3=[000]T,C4=-C2,C5=-C1;DOB参数kd=30。

选取跟踪误差最大值me、平均值μ和标准差σ共3项性能指标[26],比较不同控制器之间的跟踪效果。期望角度信号为x1d(t)=10[1-cos(3.14t)][1-exp(-t)] °,在负载质量m=0,0.25,0.5 kg共3种工况下进行实验。

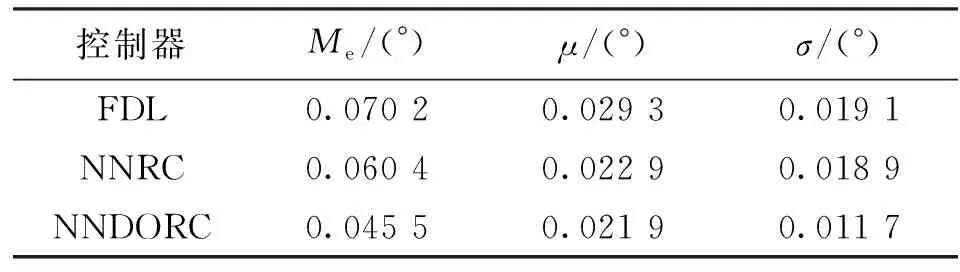
表1 m=0时的性能指标Table 1 Performance indicators (m=0)

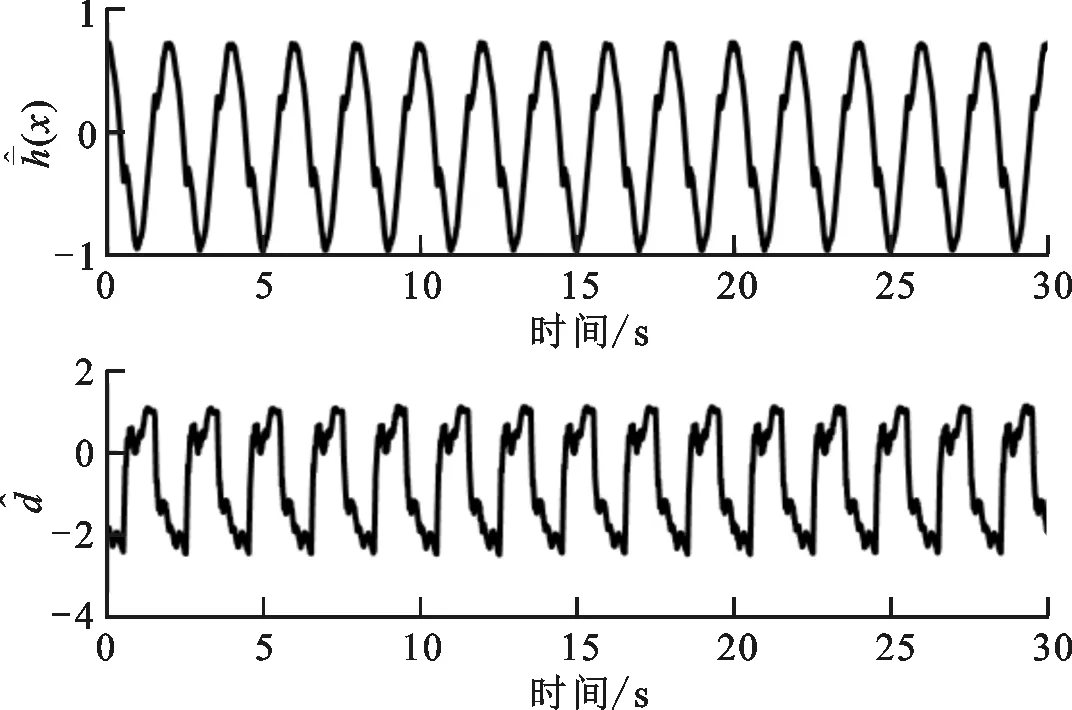
图6 m=0时NNDORC对和d的估计 and d estimation of NNDORC (m=0)

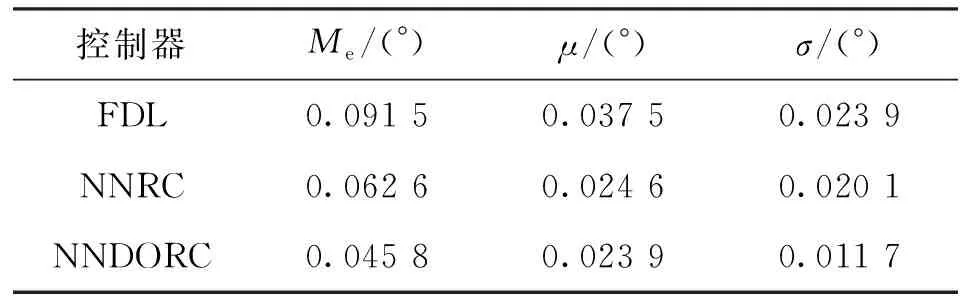
表2 m=0.25 kg时的性能指标Table 2 Performance indicators (m=0.25 kg)

图7 m=0.25 kg时3种控制器跟踪误差Fig.7 Tracking error of three controllers (m=0.25 kg)

图8 m=0.25 kg时NNDORC对和d的估计 and d estimation of NNDORC (m=0.25 kg)

表3 m=0.5 kg时的性能指标Table 3 Performance indicators (m=0.5 kg)

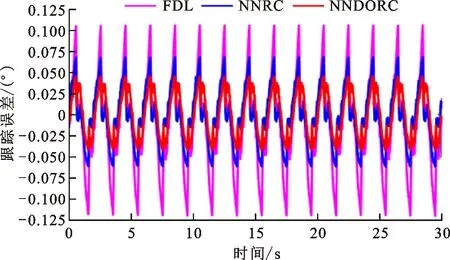
图9 m=0.5 kg时3种控制器的跟踪误差Fig.9 Tracking error of three controllers (m=0.5 kg)

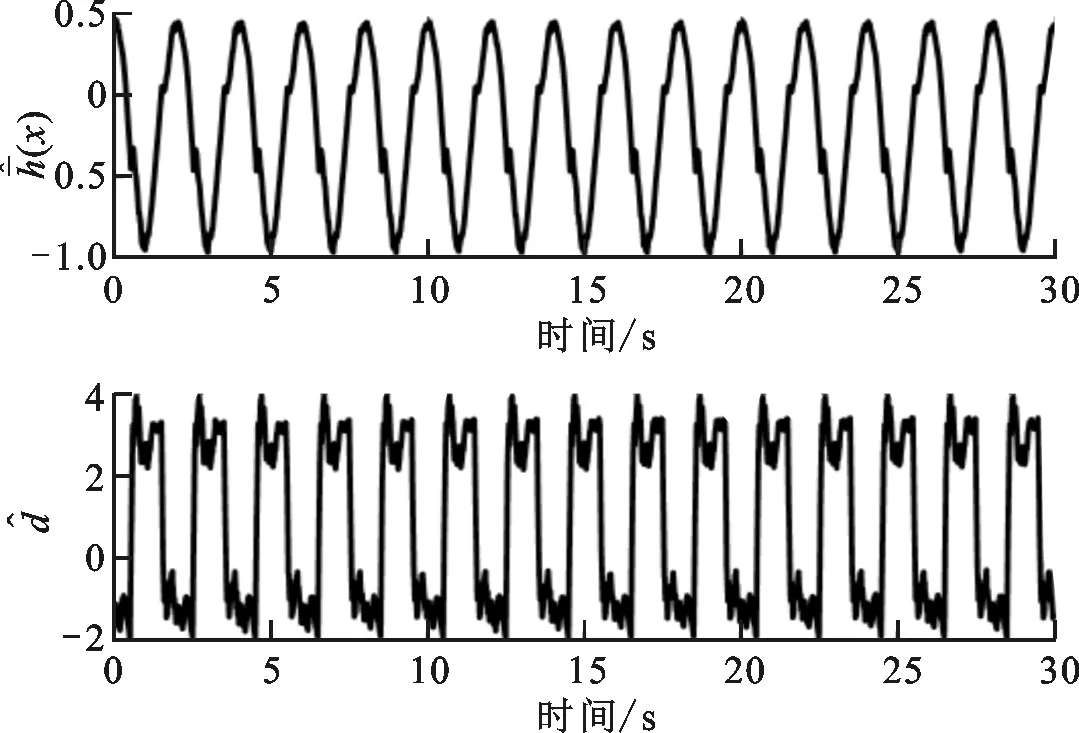
图10 m=0.5 kg时NNDORC对和d的估计 and d estimation of NNDORC (m=0.5 kg)

为了更直观地看到负载变化对3种控制器跟踪性能带来的影响,将不同控制器最后两个周期的实时跟踪曲线及Me变化进行对比,如图11所示。可以明显看出,在跟踪误差和Me方面,NNDORC能有效克服负载变化带来的影响,保持自身跟踪精度,而NNRC在无负载和小负载时也可保持一定精度,但大负载时跟踪误差明显变大,跟踪性能变差。