一类非线性波方程的潘勒韦分析、对称和精确解
2022-02-14刘汉泽李雪霞
刘汉泽李雪霞
(聊城大学数学科学学院,山东 聊城 252059)
0 引言
非线性科学主要研究自然科学和现实应用中的各种非线性现象,包括混沌、分形、孤立子与可积性等,非线性理论不仅具有重要的理论意义,而且有重要的应用价值,例如在工程、社会和经济等领域,包括财政问题、人力资源等方面,都具有重要的意义。而描述各种非线性现象的数学模型一般为非线性微分方程。因此,为了深入研究相关领域的各种实际问题,研究非线性微分方程的各种精确解就显得非常必要,因为它有助于人们定量地理解各种非线性现象的物理与实际意义,并用于指导实践。同时,精确求解各类非线性方程也是非线性科学研究的重要任务之一。到目前为止,已产生大量的求解非线性偏微分方程精确解的有效方法,如对称分析、不变子空间法,可积系统方法,包括达布(Darboux)变换与贝克隆(Bäcklund)变换,动力系统方法与各种待定函数法等。其中,潘勒韦(Painlevé)分析[1-4]与对称分析[5-10]是研究非线性方程的系统有效方法,在非线性系统的求解与可积性研究中起着重要的作用。
M.Kowlczyk等研究了一类重要的Φ4模型[11],该模型在物理、非线性理论以及工程应用等领域有着重要的意义[11-13]。但是,相关文献迄今未见利用Painlevé分析或对称分析的研究结果。本文首先对原方程加以推广,使之更一般化。然后,利用Painlevé分析与对称分析相结合的方法,研究如下的非线性偏微分方程u xt=au+bu p,(1)其中u=u(x,t)为未知函数,x、t是自变量,a、b、p为任意实数且b≠0,p≠0,1(否则,方程为线性)。方程(1)也是一类重要的非线性波方程,主要描述一些非线性波的运动规律。在应用物理、非线性光学、非线性波理论等领域有着重要的应用背景,这类方程也是动力系统与可积系统研究的重要对象之一。在本文,作者首先利用潘勒韦分析,得到方程的潘勒韦性质并给出了在一定条件下的贝克隆变换与截断展开解。然后,利用李群分析给出方程的所有点对称,最后,研究方程的对称约化与群不变解。
1 方程(1)的潘勒韦分析
在本节中,我们对方程(1)进行潘勒韦分析。为此,首先假定指数p为大于1的正整数。设

其中u j=u j(x,t)为系数函数,φ=φ(x,t)≠0为任意解析函数且u0≠0,k为正整数,(2)也称潘勒韦展式或罗朗展式(罗朗级数)。将(2)代入方程(1),由首项分析,得到

由(3)可知,若k、p均为正整数,有且仅有以下两种情形:当p=2时,k=2;当p=3时,k=1。综上,可得如下结论。
定理1 若方程(1)具有潘勒韦性质,则p=2或p=3。
此定理给出了方程(1)潘勒韦可积的必要条件,否则,方程不可积(不具有潘勒韦性质)。
下面,对以上两种情形分别讨论。
(1)当p=2时,k=2。此时,把潘勒韦展式(2)代入方程(1),可得


亦即u1=u1(x,t)满足方程(1),由此即得。
定理3 当(22)满足时,(21)为方程方程(1)的贝克隆变换。
特别地,在方程(1)中令a=0,由上述讨论可得非线性方程u xt=bu p的潘勒韦性质,此处从略。
2 方程(1)的对称分析
本节,我们研究方程(1)的对称性,并给出它的所有点对称。为使结论更具一般性,只需假定方程的所有参数a、b、p为任意实数。首先,设方程有如下形式的向量场

需要说明的是,第一,方程的的对称与系数a、b及指数p无关,只需假定系数b≠0及指数p≠0,1即可;第二,(26)包含了方程(1)的所有点对称。
下面,讨论方程的对称约化。为此,只需考虑以下两种情况
(1)对于V=c∂x+∂t,可得对称变换u=f(η),其中η=x-ct(c表示波速)为不变量,它对应行波变换。代入方程(1),得

其中导数表示对不变量η求导。
(2)对于V=x∂x-t∂t,可得对称变换u=f(η),其中η=xt为不变量。代入方程(1),得

其中导数表示对不变量η求导。这样,通过上述两种不变量,分别将方程(1)约化为常微分方程(27)及(28),从而将偏微分方程的求解转化为常微分方程的求解。
3 非线性波方程的精确解
在本节中,利用对称约化,研究非线性方程(1)的精确解,以p=3为例,其它情况可类似考虑。此时,方程(27)为
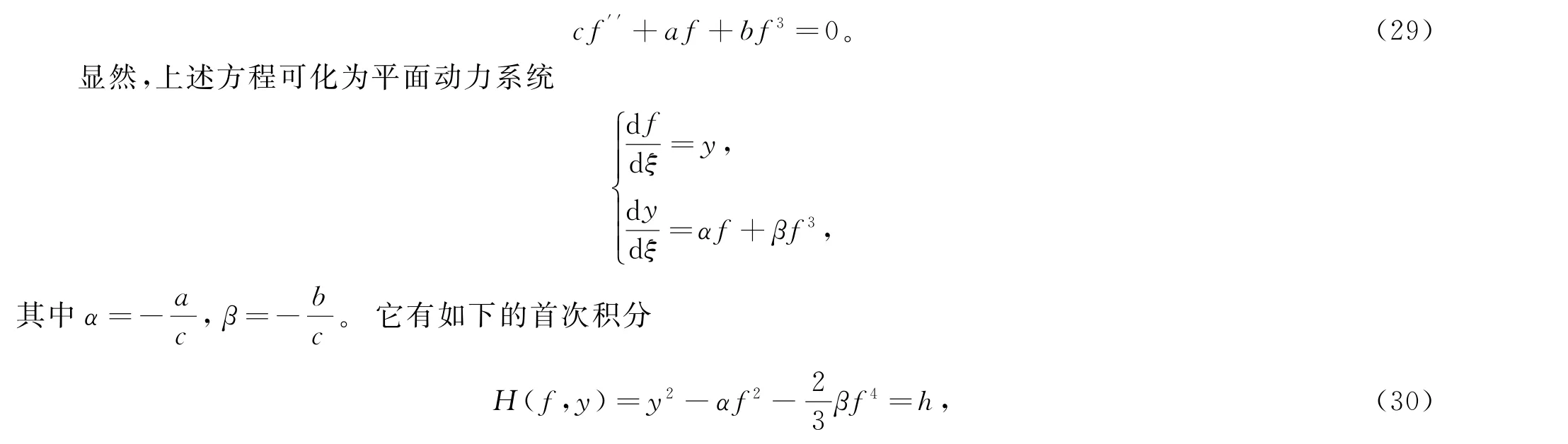
其中h为任意常数。从理论上说,求出了首次积分,也就相当于得到了系统的通解[14],从而得到原非线性波方程(1)的解。下一步,可通过两条途径得到显式解,一是对首次积分直接积分,得出通解,二是基于首次积分,利用动力系统方法分析系统的奇点与分支,进而得到系统的各种行波解[14-16],本文从略。
当p=3时,方程(28)为


所以,方程(31)的幂级数形式的通解可表示为f(η)=k1f1(η)+k2f2(η),其中k1,k2为任意常数。相应地,可得非线性波方程(1)的解为u=f(xt)=k1f1(xt)+k2f2(xt),其中f1、f2分别由(32)、(35)给出,其系数分别由(33)、(37)依次给出。
4 结论
本文应用潘勒韦分析得到了方程(1)的可积性(潘勒韦可积),并给出了当方程满足一定条件时的贝克隆变换及截断展开解。进一步,研究了方程(1)的对称性,得到了方程所有的点对称。基于对称约化,研究了方程的群不变解,包括行波解。最后需要指出的是,潘勒韦分析和对称分析是研究非线性方程精确解与可积性的系统有效方法,其中还有许多问题可以进一步讨论,例如方程的广义对称性、完全可积性以及更多形式的精确解等,都是今后可以研究的内容。
