d-维环面上分数阶薛定谔方程解的长时间稳定性

2022-02-14弭鲁芳邬小清

聊城大学学报（自然科学版） 2022年3期

弭鲁芳邬小清

(1.滨州学院理学院,山东滨州 256600;2.大连理工大学数学科学学院,辽宁大连 116024)

0 引言

考虑d-维分数阶薛定谔方程

定理1 给定任意的r≥4,则存在正测度集合F⊂Wμ,使得对任意的V∈F,存在依赖于r,μ的正数p∗(r,μ),对任意的p≥p∗(r,μ),存在∈∗(r,μ,p)使得下面的结论成立:如果初值u(x,0)满足∈:＝||u(x,0)||H p≤∈∗(r,μ,p),则有||u(x,t)||H p≤2∈, ∀|t|≤∈－r。

我们将利用无穷维哈密顿系统的Birkhoff标准型理论来证明定理1。该理论是研究哈密顿偏微分方程解的几乎全局性的有力工具。Birkhoff标准型技巧经由Bambusi,Berti,Delort,Grébert等学者的充分研究,发展已近趋完善[2,5-18]。

在文献[9]中,Bambusi-Grébert证明了一个抽象的Birkhoff标准型定理。该定理可以应用到一大类满足所谓的Tame性质的哈密顿偏微分方程上,进而在Sobolev空间H p中得到了小初值解的多项式长时间稳定性。具体来说,对任意的r＞0,及任意的充分大的p(p依赖于r及某种非共振条件),存在ε(p,r)及正常数c使得如果初始值满足ε＝‖u(0)‖p≤ε(p,r),则有

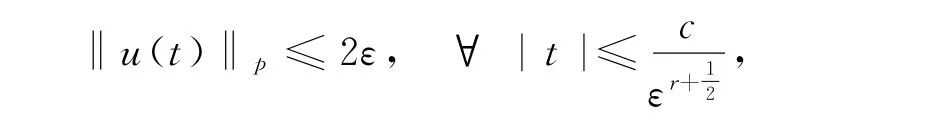
之后,Bambusi-Sire仿照文献[9]中发展的方法证明了s＞1/2的分数阶薛定谔方程(1)的几乎全局解的存在性[2]。很自然地会问,对于0＜s＜1/2的情况,这种长期稳定性结果是否仍然成立,这是作者在文献[2]中提出的一个问题。这两种情形主要的不同点在于当s＞1/2时,频率的所谓的分离性仍然按照下述方式成立:对任意的i≠j,随着i,j→∞有下述不等式成立

上面的估计保证仅有有限多个共振集(当然依赖于r和N)。详细证明过程可参见命题1中情形3的证明。鉴于上述发现及受Pöschel[29]研究波方程拟周期解的存在性时建立的非共振条件的启发,建立了(γ,r,N)-非共振条件(9)得到了高阶的部分标准型,用于研究原点附近解的长时间行为。

注1 此处,零动量性质和频率的次线性增长对于保证估计式成立是非常重要的,而估计式(4)的成立又保证了仅有有限多个共振集合,从而使得测度估计部分成立。

关于偏微分方程解的长时间稳定性一直是国内外学者关注的热点问题,最近的一些新结果为Birkhoff标准型开辟了新的方向:(1)Biasco-Masseti-Procesi[30]证明了在适当的丢番图条件下具有外部参数的圆上的一维NLS在Sobolev范数下的指数稳定性结果;(2)Bernier-Faou-Grébert[31]构建了一个无外部参数的有理标准型,显示了一维NLS小解的稳定性;(3)Bernier-Faou-Grébert等人[32]证明了仅含一个参数的d维非线性波动方程的长时间稳定性结果,里面介绍了一些新的非共振条件和一些新技术;(4)水波方程和完全非线性NLS的长时间存在性结果,里面考虑了拟线性情况和分数阶色散关系,这使问题更加困难[11,33-35]。除此之外,也有一些工作涉及平面波解、d-gap解或KAM 环面的长时间行为[16,36-39]。