基于非回溯矩阵的有向网络拆解方法

王士海卓新建王文璇李慧嘉

(北京邮电大学理学院,北京 100876)

0 引言

在复杂性科学中,一个网络(图论中表示为G＝(V,E))是由n个节点组成的节点集V和m条节点间的边组成的边集E组成[1]。对于Internet、WWW、大型电力网络、交通运输网络和人际关系网络等许多真实世界的网络都可以由用这种简洁的方式来建模研究[2],通过这种方法可以将这些网络看作是一个具有独立特征又与其他个体相互连接的节点的集合,每个个体视为网络中的节点,节点间的连接视为网络的边,这种抽象的方法可以直观地展示真实网络的拓扑结构,也为深入了解真实网络的状态和功能提供了一个有效研究手段。

但随着科技与社会的不断发展,流行病毒[3]、计算机病毒[4]、谣言传播[5]或是贪污腐败[6]在人类世界中产生更加严重的负面效果。然而,移除或者停用一部分网络中的点将网络分解为几个隔离的子部分就可以有效地保护网络的鲁棒性和控制网络中动力学行为,对上述所说的网络中的负面影响加以遏制,已经有实验证明这种方法可以有效地免疫人群中流行病的传播[7],阻止社交网络中谣言的传播[8]和防止计算机网络中病毒的扩散[9]等。在复杂网络科学中存在着一些研究,它们以某种最优的方选择网络中的一组节点子集S,并探究移除S后对网络特性的影响。例如探究移除S后会使网络最大联通(强)子集怎么变化,在流行病传播或网络病毒传播中,如果先将S隔离或者感染对病毒传播速度有什么影响等。在实际情况中,选择并移除网络中的节点子集S往往会产生一定的成本耗费C,在流行病传播模型中对于节点的疫苗接种需要一定的社会经济花费,在计算机病毒或者舆论传播网络中移除不同的节点集在实际情况中耗费的资源也不同。因此产生了一个组合优化问题:在约束移除节点子集S对网络的影响下,使移除成本C最小化。并且移除节点会破坏网络结构进而影响网络功能,因此我们需要尽可能少地移除节点,找到一组移除成本C最小的节点即最小拆解集(在本文中我们考虑拆解成本为单位成本这种最普遍的情况,即最小拆解集为节点个数最少的集合)并移除后将网络分解成不相通的多个子部分就是网络拆解[10]。找到最小拆解集是一个NP-hard问题[11],对于这种问题,目前只能寻求有效的近似算法或启发式算法,对于拆解问题已经有一些基于节点的度或中心性的递归算法,例如2015年提出了名为“集体”影响力(CI)[12]的启发式算法,其根据节点的度数和局部邻居节点的度决定无向随机网络节点的归属;2016年Alfredo Braunstein提出了拆解大型随机无向网络的三段最小和(min-sum)算法[10],对于大型无向随机网络,此方法是比较有效的拆解算法;2019年又有任晓龙提出了针对无向权重网络的网络通用拆解算法(gnd算法)[13],此方法考虑当节点的拆除花费等比于节点权重而为非单位费用的情况,先对网络进行算子为节点权重拉普拉斯矩阵的谱划分,划分成功后对于连接不同划分之间的边应用节点权重覆盖算法找到可以划分网络的权重最小点集,从而找到最小花费拆解集。gnd相比之前的算法更具有一般性和适用性,它考虑了无向网络中节点权重对网络拆解问题的影响。但是gnd方法中的算子为点邻接矩阵,应用点邻接矩阵的谱方法在分析有向网络的时候大多数会对称化邻接矩阵从而将网络无向化处理[14],这种处理方法不可避免地会丢失网络中的一些信息[15],导致在对于有向网络拆解的最小节点集的寻找过程中会加入一些不必要的节点进而会造成不必要的拆解。此外基于消息传递模型的拆解方法(2020年)[16]和邻居连边的敏感拆解算法(2020年)[17]等一些比较新的拆解方法和对拆解的分析[18,19]等工作。

现有的拆解算法多是在无向网络中开展,而针对有向网络的拆解工作很少,但是在如今许多的真实世界网络(如WWW 网络、熟人关系、网络电子邮件网络、文字关联网络和文章引用网络等)中的节点之间的连边是单向连接的,并不存在无向网络中的相互关系[20],现有的拆解方法有时会不适用于这些有向网络的拆解。相对于无向网络中的拆解,在有向网络中的拆解需要考虑到网络中节点连边的方向。例如在舆论传播网络中一个有向边e(图论中也称之为弧)连接的入点(Innode)为传播者时,这条边的出点(Outnode)没有被该节点传播的可能性,应用基于无向网络的拆解方法对网络拆解时有时会忽略节点间的这种单向关系,导致会对这条边e进行移除,造成不必要的拆解导致对拆解效果产生影响。传统的拆解方法忽视了这种网络的内在机理对拆解的影响,针对这个问题本篇文章应用表示边邻接关系的非回溯矩阵作为谱划分的算子,保留节点关系的有向性,并将有向网络的拆解和谱划分方法相结合,提出了改进后的有向网络的谱拆解方法(后文简称dir方法):直接应用有向网络中的边作为拆解单位,将有向网络的极大强连通子图作为拆解主体,在极大强连通子集中应用边邻接矩阵(非回溯矩阵)的谱特性来进行边模块的二划分,进而找到连接两个边模块的节点集的重叠点集作为最小拆解集来拆解网络,直到拆解到网络的指定拆解规模(最大强连通子图的节点个数)。这种拆解方法可以充分利用非回溯矩阵的优良特性,在拆解过程中可以极大程度地保护网络的拓扑结构,进而通过实验验证本文方法适用于有向网络的拆解。最后,本文中通过分析拆解过程中网络的聚类系数、同配性系数、模块度函数等网络指标的变化,来分析不同拆解方法对网络结构的影响,并通过在网络中实验验证了应用边模块划分来拆解网络可以极大程度地保留网络中的结构信息。

1 模型与方法

如图1所示本文将边模块划分与网络拆解相结合构造了有向网络中的网络拆解算法,先对网络进行边模块划分:采用非回溯矩阵储存边的邻接信息,并以非回溯矩阵作为算子构建了最小边数拆解函数,通过对函数矩阵近似第二特征向量的求解对边模块进行划分;划分后找到连接不同边模块的最小数量的边集,找到边集中模块重叠的节点集,通过移除这个节点集破坏不同模块之间的连接最终完成拆解。

图1 有向网络拆解流程图

应用本文方法对上述有向网络进行拆解:根据非回溯矩阵的谱特性对有向网络的边二划分为左右两个红蓝不同模块;找到连接这两个不同边模块的重叠节点5和6,对节点5和6进行移除并断开与之相连的边就可以将该有向网络分为两个互不相连的子部分。这种移除边模块重叠节点的拆解方法相对于之前的拆解方法所需拆解步骤更少,不需要找最小节点覆盖集,并且对应的拆解花费更少(应用传统分解方法找到的点为5、6、7、12),更适用于有向网络。

1.1 非回溯矩阵

在有向网络G中,i、j、k、l都为V中的节点,根据非回溯随机游走的定义,只有当j＝k,并且i≠l,有向边i→j与另一条有向边k→l相连。在有向网络中B是一个m∗m的非回溯矩阵,本文用这个非回溯矩阵来表示有向网络中的边的邻接关系,定义为

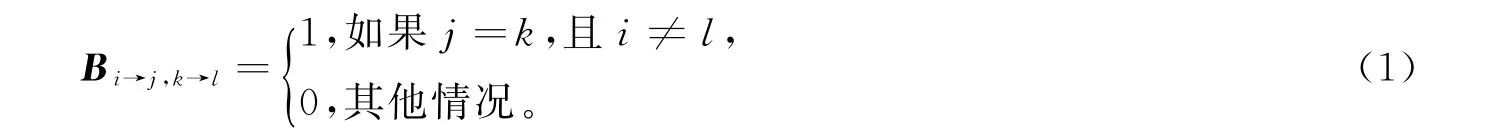
非回溯矩阵B不同于邻接矩阵A,B将每条有向边作为元素,在矩阵中表示边之间的相互邻接关系,所以又被叫做边邻接矩阵,在文章[21]中已经表明非回溯算子的优秀特性,它的谱特性与点邻接矩阵A或者其他矩阵相比在网络中都有更好的性能表现,特别是它的第二特征向量对于网络结构划分所表现出的强分离性;与此同时,真实世界中的有向网络往往具有比较稀疏的结构和较大的规模,本文中我们所应用的非回溯矩阵B相比于点邻接矩阵A在稀疏网络中也具有良好的表现。B作为边的邻接矩阵,矩阵中存放的是网络中边之间的联系,对网络中的节点的信息并不敏感,从而避免了拆解时倾向于移除度比较大的节点从而造成破坏网络的连通子集的情况[22],从而最大限度地保留了有向网络中的结构信息。并且通过实验证明了应用非回溯矩阵进行拆解保存有向网络中边的单向连接关系,降低节点的拓扑信息对所选拆解点集的扰动,有效避免直接使用有向网络邻接矩阵来做谱算法算子时的网络信息丢失问题。

1.2 拆解目标函数

在这部分我们考虑将网络按照边的性质划分为两个相等规模模块的一般情况下,最小化两个不同模块间的边的数量。我们已经应用非回溯矩阵储存有向网络中边邻接信息,因为在拆解问题中我们所最终要移除的是不同边模块上所有重叠的节点,边的权重对最小节点集的选取不造成影响,所以我们设定每条边的权重为单位权重。我们将边网络中的m条边根据对应的特性二划分为两个相等规模m/2模块。我们对于网络中任意一条有向边i→j,i,j∈N定义一个指标变量s i→j∈R m,并假设如果这条边i→j属于划分模块1,则s i→j＝1;如果边属于划分模块2,则s i→j＝－1。所以我们得到

1.3 划分向量

由于大规模网络连边很多,它对应的B的第二特征向量很难精确得到[24],本文中我们应用传统的幂律迭代模型来进行对第二小特征值的简单精炼的近似算法。对于矩阵B′,B′有m个实非负特征值0≤λm～＝2dmax－λm≤…≤λ2～ ,其对应的特征向量为v(1),v(2),…,v(m),是R m空间上的正交基,我们定义矩阵B中元素的最大度为dmax,x,y代表矩阵的行列,通过计算1-范式我们得到谱上界。

算法1 近似特征向量算法输入:非回溯矩阵B,网络边数m,v 1 ＝(1,1,…,1)T输出:近似第二特征向量v 1:随机在单位球面上选取向量v;2:v ←v－v T v v T v 1·v 1;3:For i＝1 toτ(m);4: v ←B～v||B～v||;5:End for;6:返回v。

算法2 有向网络拆解算法(dir方法)输入:网络G输出:最小拆解集L S,最小拆解费用c 1:选取网络中最大强连通子图GSC 并根据式(1)计算其非回溯矩阵B GSC;2:初始化L S、c 为0;3:利用公式(3)计算B GSC对应的B′;4:利用算法1获得划分向量v(2)并二划分最大强连通子图为两个边模块;5:找到连接两个边模块的边集,创建划分子图;6:找到划分子图中重叠点集S;7:将S 从网络G 中移除,并更新网络G;8:将S 并入L S,并更新L S、c 以及B GSC;9:如果最大强连通子图的规模GSCsize＜目标拆解规模C,返回L S和c;否则,回到步骤3。

1.4 有向网络拆解

算法2提供了一个可以将网络重复地拆解到指定规模的递归解法。我们将拆解规模规定为极大强连通子集GSC中点的个数,在这个算法中我们意图将有向网络拆解至拆解规模小于目标规模C,根据此思想我们定义上述算法。算法输入是有向网络的点边拓扑结构,最后的输出是将此有向网络拆解到指定规模时的最小节点拆解集和所需要的拆解花费;算法的第1步先将网络的极大强连通子集作为有向网络的拆解主体,这样可以过滤掉网络中与网络拆解无关紧要的节点及边,提高有向网络的拆解效率,并且选取强连通子集作为拆解主体可以直接与常用的无向网络的连通子集形成对比,可以避免将网络无向化来满足无向网络拆解条件从而造成多余拆解;通过判断网络的极大强连通子集的规模来控制流程的进行;第2步将最小拆解集和拆解花费初始化为0算法的第3步生成最大强连通子图的非回溯矩阵的拉普拉斯矩阵以便对边模块的下一步划分;第4步通过计算＝2dmax－B′,并应用特征向量近似算法求得第二特征值所对应的特征向量,用来对边模块进行划分;5、6找到边模块间重合的节点集并在整个网络G中进行移除,第7步将要移除的节点加入拆解集并更新网络最大强连连通子集和拆解集;第八步更新最小拆解集以及拆解花费;第9步判断网络的最大强连通子集规模是否达到目标拆解规模。此递归算法可以得到把有向网络拆解到指定规模的一组最少的不同边模块之间连接的节点集。

1.5 算法复杂度

本文应用的近似特征向量的时间复杂度等于迭代次数τ(m)乘以矩阵B～与向量v之积的复杂度,即O(τ(m)m2),其中m为网络边数。

2 实验结果

为了验证本文提出的dir方法在有向网络中的适用性,我们将其应用在人工有向ER 网络和BA 网络以及真实网络中,并将拆解结果与两种比较常用的方法(gnd算法和min-sum 方法)进行比较,实验选取了表1的数据集,在不同的人工有向网络和大规模的真实网络中进行实验对比(为了方便比较,文中的拆解规模和拆解花费均为所占比例)。

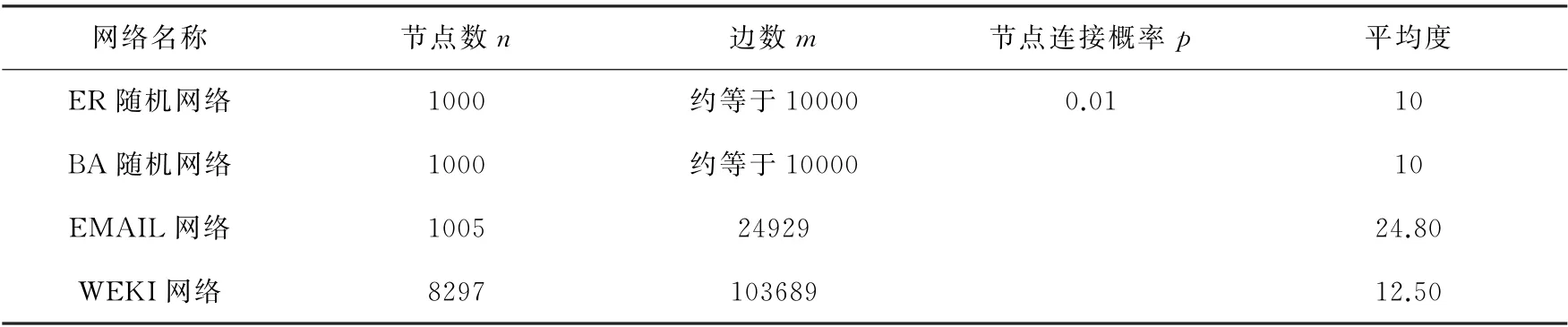
表1 网络数据集

任晓龙等学者[13]在之前的文章中已经证明了在无向网络中当网络拆解花费为单位花费(节点个数)和非单位花费(基于节点度)时gnd方法相比与min-sum 和信息传递等其他算法都有较高的拆解效率,当拆解规模相同时gnd方法比其他算法有更低的拆解花费,gnd可以以更小的拆解花费对网络结构进行更大的破坏,该方法在无向网络的拆解中相对其他算法有着比较好的表现,本文将dir方法与gnd方法和min-sum 方法进行实验比较。

图2和图3是不同方法在不同有向网络中的拆解结果,给出了拆解规模和拆解花费的对应曲线图,纵坐标拆解规模为最大(强)连通子图的节点数占比,横坐标拆解花费为拆解到纵坐标所示规模时最小拆解集的节点数量占比。如图2所示,在比较稠密的ER 随机网络中,当所需拆解规模小于0.25时,dir方法拆解花费比gnd与min-sum 方法所需的拆解花费都要小;在平均度为10的人工BA 有向网络中dir方法拆解花费则明显小于其他两个方法。并且在比较稀疏的真实有向网络中(图2)进行拆解实验时,将网络拆解到同一指定规模时本篇文章所提出的方法所需要的花费要少于其他方法,产生区别的原因是gnd与min-sum 等方法将网络中的最大连通子图作为拆解主体,本文所提出的方法将网络的最大强连通子集作为拆解主体,当网络足够稠密时应用有向网络中的最大强连通子图和连通子图的规模差别不大,但在比较稀疏的网络(比如WEKI网络)中时,应用有向网络的最大强连通子图进行拆解的花费要明显低于gnd与dir方法。实验表明了本方法在有向网络中进行拆解的花费少的优越性,说明本文提出的方法在有向网络的网络拆解的高效性。

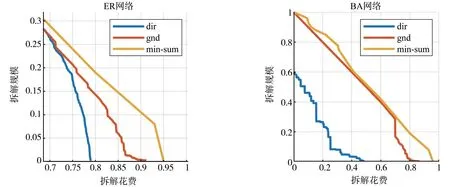
图2 有向ER 随机网络和有向BA 随机网络拆解花费与拆解规模对应曲线图

图3 有向真实网络拆解花费与拆解规模对应曲线图

接下来探究本文中所提出的不同拆解方法对网络结构的影响,通过将不同拆解方法应用到不同网络中,并通过比较拆解过程网络的聚类系数[25]和同配性系数[26]来证明本文方法对网络结构信息可以极大限度保留的优越性。

图论中聚类系数用于衡量节点聚集的程度。有证据表明,大多数现实世界的网络中,特别是在社交网络中,节点倾向于创建相对紧密联系的群体;这种可能性往往大于在两个节点之间随机建立关系的平均概率,对于一个网络G＝(V,E),形式上由一组节点和节点之间的连边组成,边连接节点。一个节点v i的邻域N i被定义为其紧邻的节点,N i＝{v j:e ij∈E∨e ji∈E}。有向网络中一个节点的局部聚类系数C i为

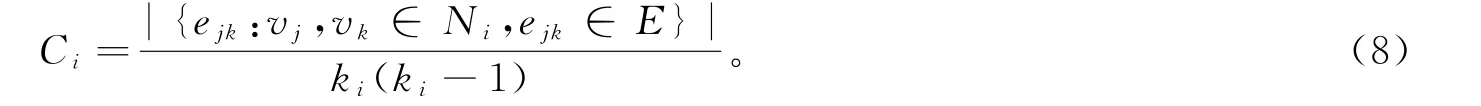
作为全局聚类系数的代替,Watt和Strogatz[20]将所有顶点局部聚类系数的平均值作为网络整体聚类水平

在这里我们通过观察拆解过程中网络全局聚类系数的变化来比较dir与其他两个拆解方法对网络中节点连接程度的影响进而探究对网络结构的影响。

实验首先对人工ER 随机网络和BA 网络进行拆解,拆解花费与聚类系数关系图由上图4所示,在人工ER随机网络中当拆解花费小于0.7时,本文所提dir方法所对应的平均聚类系数的曲线相对于gnd和minsum 的曲线更为平稳,并且在BA 网络中也是先到达一个平稳状态。本文提出的拆解方法对于整个网络的聚类系数的扰动相对于gnd和min-sum 更小,这体现了本文所通过边模块划分来移除模块间重叠节点的优越性,dir对网络结构的影响相对于直接删除网络中节点的方法更小;在ER 随机网络中三种方法都会在一定时间内随着拆解的进行网络聚类系数不断上升,这是因为此时拆解已经让网络中的节点开始出现越来越多成团现象。在真实网络中进行实验得到的结果图5,可以看到在真实世界的有向网络中随着拆解花费的提高两种拆解方法都会使得网络中的聚类系数下降,这与真实网络的稀疏性有关,对真实网络的节点的拆解会使得节点间的集聚现象变少,群体间的连接变得稀疏,但依然可以从图中看出本文方法所对应的曲线比gnd与min-sum 方法更为平缓,在拆解过程中对真实网络的这种聚集现象的影响比这两种方法方法更小;并且相对而言min-sum 方法会对的网络的这种聚集现象影响更为明显,因为min-sum 方法倾会向于移除网络中度比较大的节点,对网络的结构信息保护能力较小。

图4 有向ER 随机网络和有向BA 随机网络拆解花费与聚类系数对应曲线图

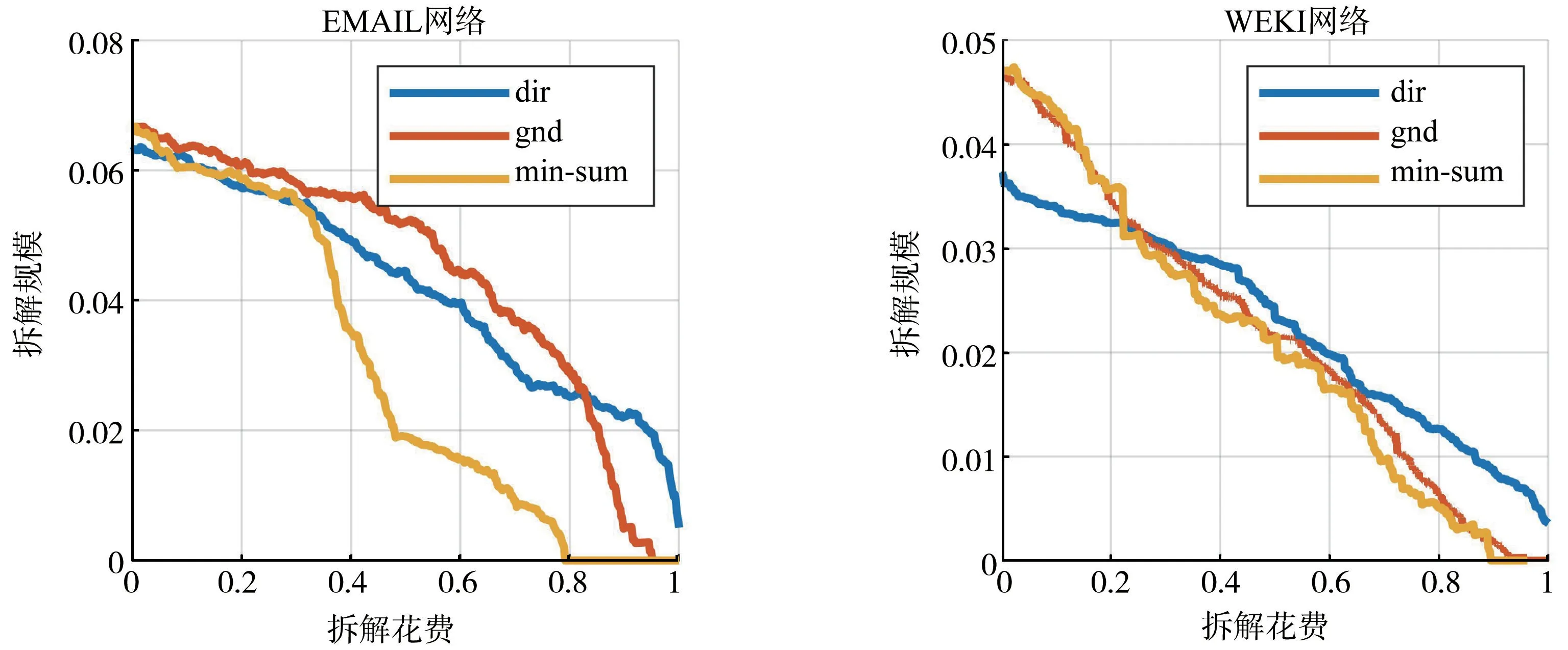
图5 真实网络拆解花费与聚类系数对应曲线图

同配性系数是用来衡量网络是同配还是异配的指标,用来考察网络中度值相近的节点是否倾向于和它近似的节点相连互相连接,可以用皮尔森系数r(度-度相关性)来刻画,r＞0表示整个网络呈现同配性结构,度大的节点倾向于和度大的节点相连,r＜0表示整个网络呈现异配性,r＝0表示网络结构不存在相关性。实验中通过观察拆解过程中对网络同配性指标的影响来分析本算法的拆解对网络结构的改变。

如图6图7所示本文所提dir方法在对网络的同配性的改变也比其他两种方法更小,无论是在ER 随机网络还是在真实网络中当拆解费用小于0.7时,蓝色曲线都更为平缓,对网络全局的同配性的改变更小,移除边模块间重叠节点对网络同配性的影响相对gnd和min-sum 方法也更小。

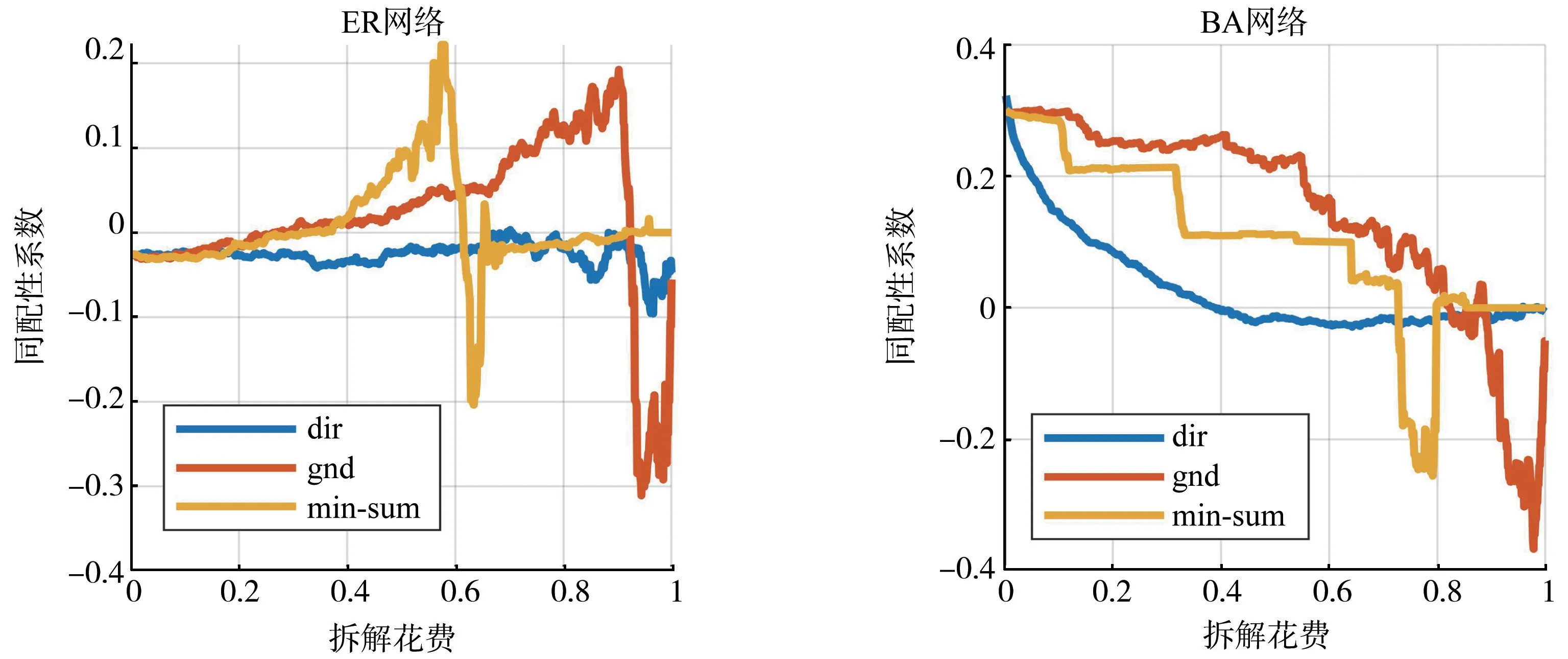
图6 有向ER 随机网络和有向BA 随机网络拆解花费与同配性系数对应曲线图

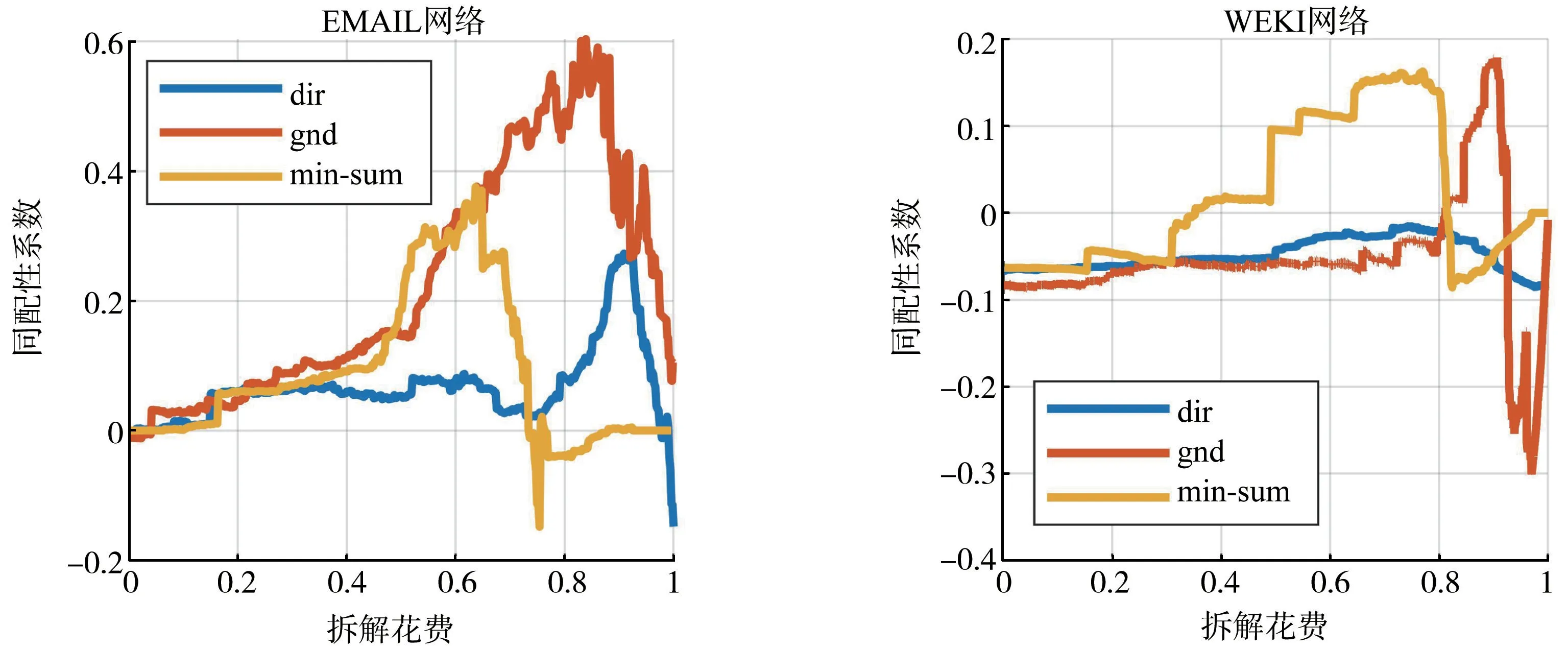
图7 真实网络拆解花费与同配性系数对应曲线图

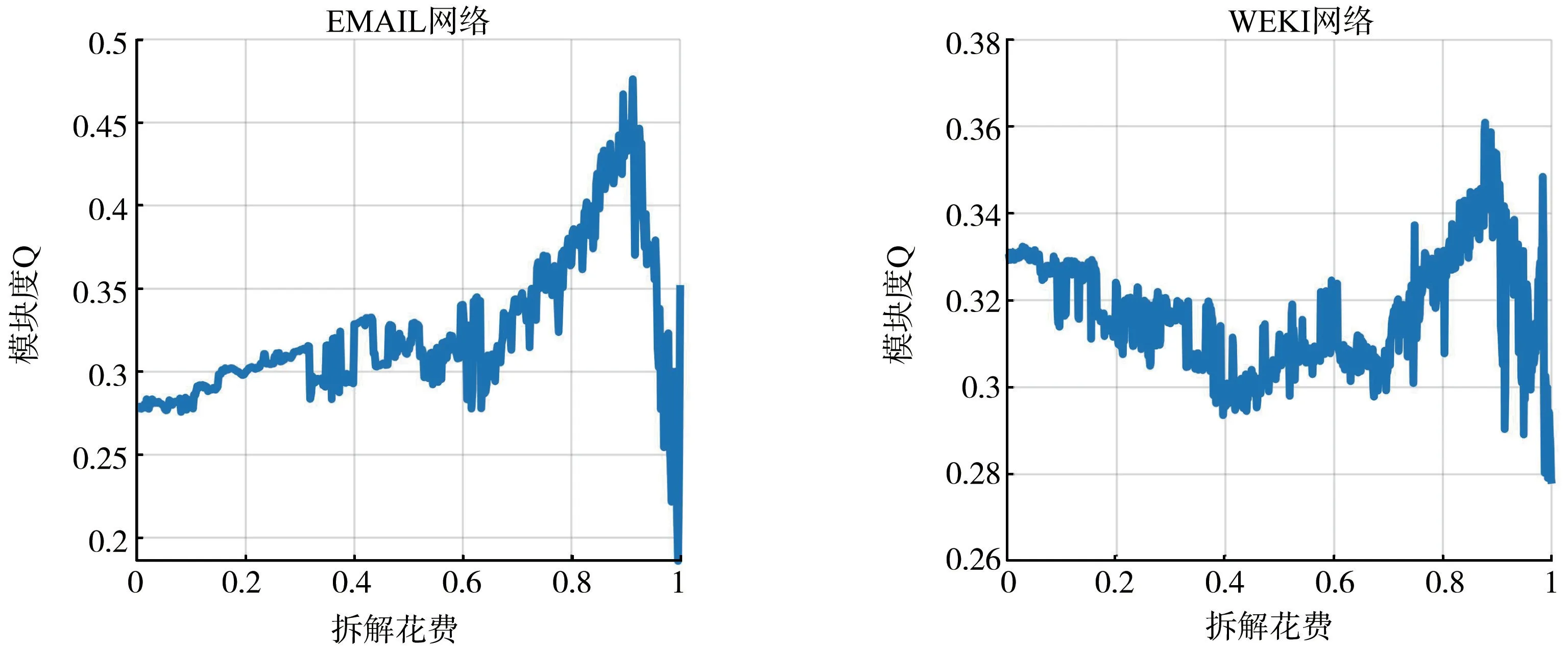
图8 真实网络拆解花费与模块度Q 对应曲线图

应用本方法拆解过程中的模块度Q的计算如图7所示,可以看到两张图片中当拆费用小于0.8的时候模块度Q随着拆解花费的变大而变大,说明拆解过程中移除点的同时也随之删掉了不同社团间的团间边,对于有效地社团划分有着一定的促进作用,当花费大于0.88时拆解会破坏掉社团内部的团间边导致模块度Q急剧下降。

综上所有实验我们提出的有向网络拆解(dir)方法无论在人工有向网络还是在真实有向网络中都有相对于gnd和min-sum 算法都有较高的拆解效率,把网络拆解到相同规模时dir法所需花费最少;同时通过比较拆解过程中的聚类系数和同配性系数也证明了本文方法可以在拆解过程中降低拆解对网络聚类系数和同配性系数的影响,有效地保留网络中的信息;也通过实验探究本文方法对网络模块度的影响,当拆解规模小于一个阈值时本文拆解方法对网络社团划分有一定促进作用。

3 结论

本篇文章针对有向网络的拆解问题提出了一个有效的拆解方法:将边模块划分与网络拆解相结合,利用非回溯矩阵构建边拆解最小拆解边数函数,通过对花费函数的特征向量近似求解找到边模块间重叠的节点进行拆解移除。本方法不同于传统的无向网络拆解方法,考虑了有向网络中的节点间的单向关系,充分利用非回溯矩阵优秀的谱特性对有向网络进行划分,在网络拆解过程中移除边模块间重叠的点也保证了拆解的效率和降低了拆解对网络总体结构的影响。并且通过将本文dir方法在不同的人工有向网络和真实有向网络中与其他方法进行实验比较,证明了dir方法在有向网络的网络拆解的高效性,同时也验证了将边模块划分应用到网络拆解中非回溯算子的应用对网络结构的低扰动。实验结果表明应用本方法对网络进行拆解可以达到较低小耗费的同时极大程度的保护有向网络中的结构信息。