含齿侧间隙及几何偏心的两级齿轮传动系统啮合特性分析∗

郭 旭，周建星，孙占飞

(新疆大学 机械工程学院，新疆 乌鲁木齐 830017)

0 引言

随着现代工业的飞速发展，多级齿轮传动系统被广泛应用于航空航天、船舶等领域，其啮合性能对于整个传动有着重要的影响.同时系统中的齿轮和轴系运行过程中传递的振动也是产生噪声的主要原因.齿侧间隙及齿轮的几何偏心会影响多级齿轮传动系统的啮合特性，因此分析齿侧间隙及几何偏心对多级齿轮传动系统啮合性能的影响具有重要的现实意义.

目前，学者们的研究主要集中在多级齿轮传动系统的建模及分析齿轮啮合过程产生振动与噪声的影响因素上[1−5]；朱丽莎等[6]为探究多级齿轮传动系统中多对齿轮的耦合状态对系统的影响，利用有限元法，建立了弯-扭-轴-摆斜的齿轮转子耦合通用模型，并对系统的固有特性及不平衡响应进行了分析；任朝晖等[7]利用集中参数法建立了22自由度的弯扭轴耦合通用模型，并研究转速、齿轮偏心距和轴向游隙等系统参数对系统振动响应的影响；马辉等[8]将齿轮有限单元法与转子有限单元法相结合，建立了多平行轴通用齿轮转子有限元模型，并分别研究了齿轮几何偏心及转子质量不平衡对系统动态特性影响；李创等[9]等利用Adams建立了含齿侧间隙齿轮传动系统的集中质量模型，研究分析了侧隙和齿轮偏心量对啮合力的影响作用；杜坤等[10]利用ANSYS/LS-DYNA有限元软件对考虑齿侧间隙的齿轮传动系统进行啮合分析，研究了不同侧隙对齿轮啮合冲击力的影响；常乐浩等[11]利用有限元方法建立了计入箱体柔性的齿轮-转子系统耦合模型，并通过单级的斜齿轮传动算例，与前人文献中的实验数据进行对比，验证了模型的有效性；周建星等[12]通过研究单级齿轮减速器，以轴承载荷作为激励源，构建了减速器齿轮传动系统有限元模型，并利用FEM/BEM法对减速器进行噪声辐射分析；Chen等[13]以行星齿轮为研究对象，考虑了齿轮时变啮合刚度等因素，构建了行星传动系统动力学模型，深入研究了轴向的偏载对齿面接触特性的影响以及对整个行星齿轮传动系统动态特性的影响；乔自珍等[14]考虑传动轴的柔性，并计入两级齿轮相位角等因素.利用有限元法建立了多源激励下的两级齿轮传动系统的动力学模型，并通过试验验证，证明了该模型的有效性；赵昕等[15]采用集中质量法建立了计入弯扭耦合的16自由度非线性动力学模型，模型中考虑了几何偏心及齿轮的时变啮合刚度等非线性因素，以龙格-库塔法进行求解，深入分析了齿轮的几何偏心对系统扭转振动响应的影响；马登秋等[16]利用Adams建立了包含几何偏心激励的圆弧齿线圆柱齿轮的动力学模型，并对偏心情况下不同的三种工况进行深入讨论，研究了偏心激励对系统啮合力的影响；林梅彬[17]利用集中质量法建立了计入齿面摩擦和齿侧间隙的单自由度齿轮系统，用龙格-库塔法进行求解，并分析了系统动力学响应的分岔特性和系统在参数平面的动态特性；Fabio等[18]提出了一种考虑叶片数和转子-定子间隙变化对碰摩力影响改进的航空发动机叶片-机匣碰摩模型，并将Newmark-β法与改进的Newmark-β法结合，得到了碰摩故障下的系统动力学特性，通过试验和仿真结果对比，结果吻合较好；王胜男等[19]利用集中质量法，建立了二级平行轴齿轮箱传动系统的平移-扭振模型，用FEM/BEM法对箱体的辐射噪声进行了分析和预测，并通过试验验证了该噪声预测方法的有效性.

在上述研究的基础上，本文以两级直齿圆柱齿轮传动系统为研究对象，基于系统质量不平衡建立转子有限元模型、与包含不同承载形式的滚动轴承模型及考虑几何偏心的齿轮有限元模型相结合，同时考虑齿侧间隙和两级装配位置关系，建立了含齿侧间隙及几何偏心的两级齿轮传动系统动力学模型，分析了系统的固有特性，并进一步探究了齿侧间隙和齿轮几何偏心对系统啮合特性的影响.

1 两级齿轮传动系统模型

两级齿轮传动系统动力学模型如图1所示，系统的有限元模型由轴承单元、啮合单元、轴段单元所组成.为计入装配和位置关系等影响因素，同时考虑轴的几何形状和尺寸.为避免出现局部振型，设定有限元节点的选取规则如下：对于轴节点一般选为轴的端点、传动轴截面突变处或是齿宽两侧的端点；齿轮节点一般选在齿宽中点处；轴承节点一般选为在滚动轴承宽度方向的中点处，最后根据实际物理关系连接起来.系统有限元模型如图2所示，齿轮箱中各轴、齿轮、滚动轴承的具体参数与文献[14]保持一致.

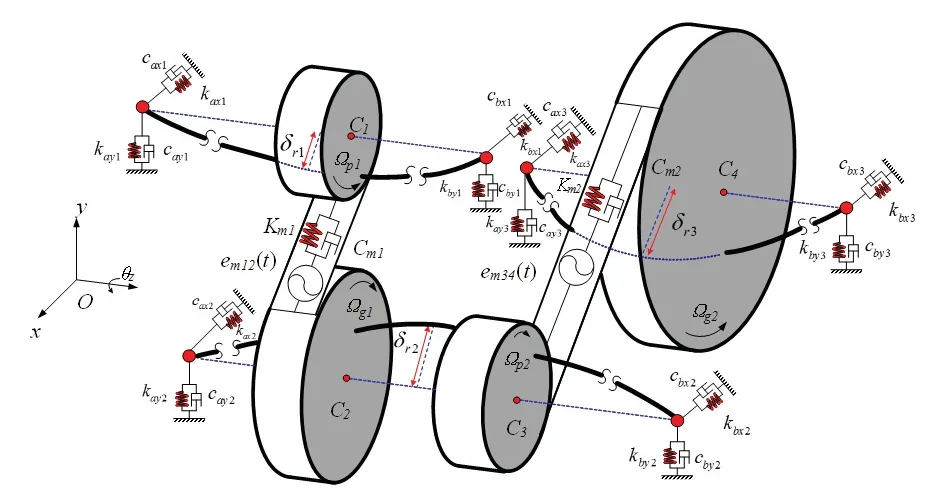
图1 传动系统动力学模型

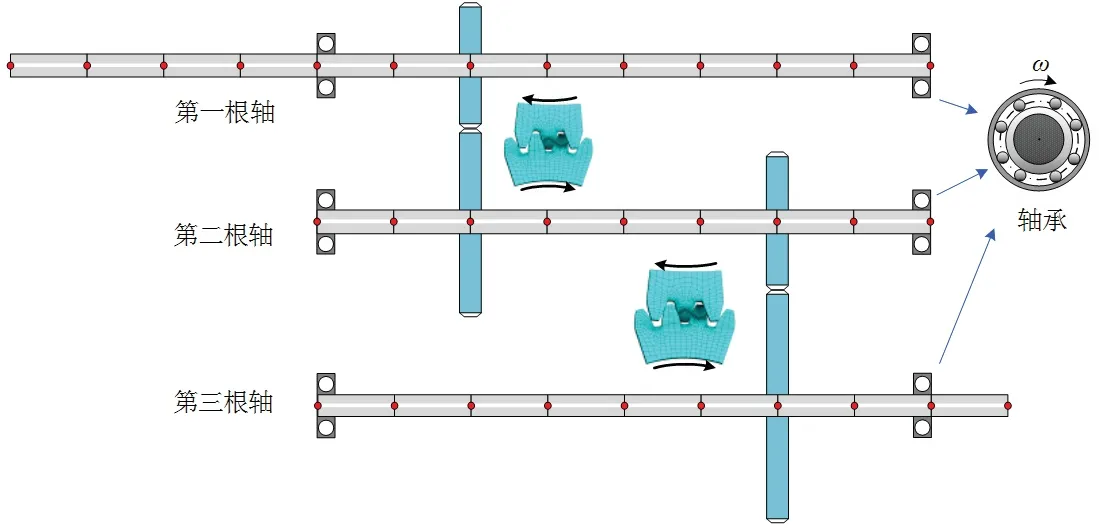
图2 两级齿轮传动系统的有限元模型

1.1 考虑质量不平衡的轴段单元

本文选用Timoshenko梁模型作为轴段单元的有限元模型，如图3所示，每个轴段单元有六个自由度：

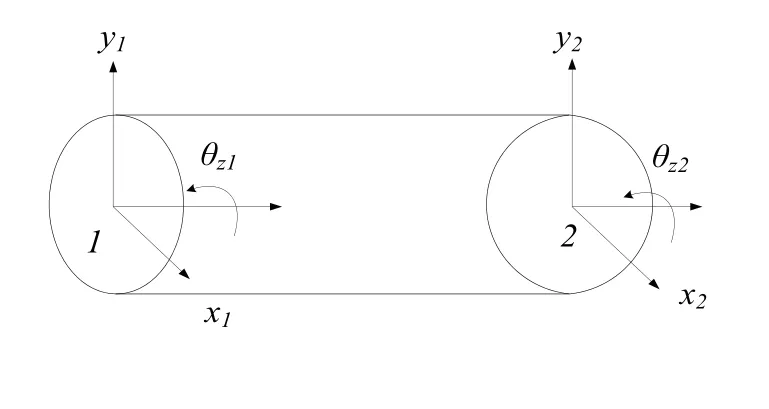
图3 Timoshenko梁模型

假设系统初始处于完全平衡状态，随着转速的提高，在系统质量不平衡力作用下，传动轴会偏离连接两端轴承中心的连线，根据转子动力学理论[18]可得：

其中：mu为轴段单元质量；ω为传动轴转速；r为传动轴中心至两端轴承中心连线的距离；Fu为轴段单元上的质量不平衡力.

1.2 齿侧间隙

一般以齿侧间隙[9,15]分段函数f()来表征齿侧间隙与齿轮副沿着啮合线方向上的相对位移之间的关系：

其中：b为齿侧间隙；¯xpg为齿轮副沿着啮合线方向上的相对位移.当>b时，齿轮副处于正常啮合状态；|¯xpg−b|≤0时，齿轮副处于脱齿状态；<−b时，齿轮副处于背齿啮合状态.

1.3 考虑两种承载形式的轴承单元

深沟球轴承的各个钢球在转动过程中，会依次通过承载区域，钢球从开始承载发生形变到产生最大径向变形，再到恢复原状的过程中，会呈现奇压、偶压两种不同的承载形式，轴承单元的时变刚度推导过程详见文献[14].

1.4 考虑齿轮副偏心的啮合单元

考虑齿轮副的几何偏心，建立齿轮系统的动力学模型，如图4所示，C1、C2分别表示主、从动轮的几何中心；θ1、θ2分别为主、从动轮的初始偏心相位角；O1、O2和e1、e2分别表示主、从动轮的质心和偏心距；xp,yp,θp,xg,yg,θp则分别表示主、从动轮的平动及转动自由度.

图4 齿轮啮合单元动力学模型及时变刚度曲线

时变啮合刚度具体计算流程见文献[13]和文献[19].由于齿轮存在几何偏心，故将齿轮副的广义位移向啮合线所在方向上投影：

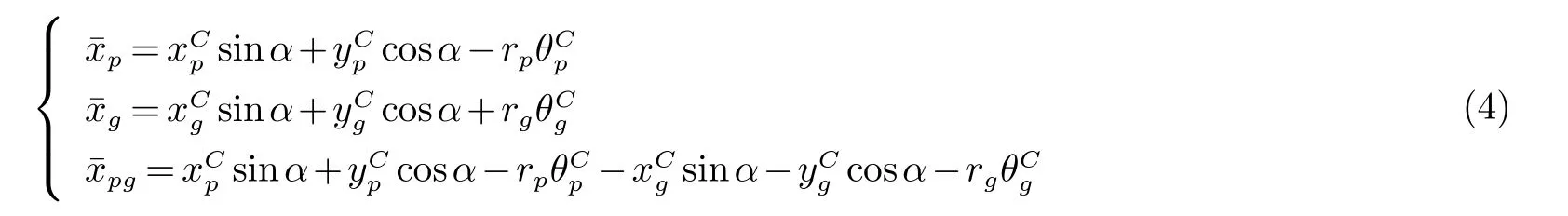
其中：rp为主动轮的基圆半径，rg为从动轮的基圆半径.偏心啮合单元在啮合线上的弹性啮合力为：

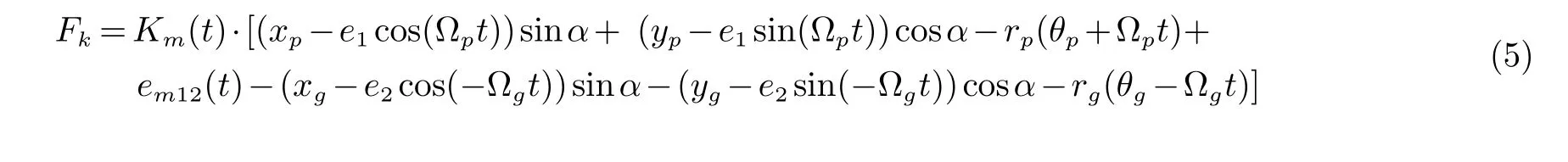
其中：Km(t) 为第一级啮合单元的时变刚度阵，其具体形式见式（6）.

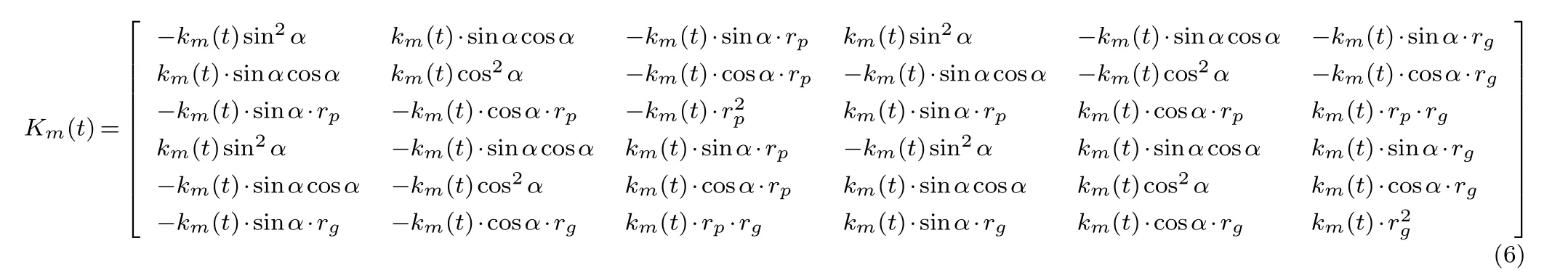
em12(t) 为啮合单元沿啮合线方向的综合误差，其具体形式如下：

其中：e0为齿轮综合误差的常值；empq为齿轮综合误差的幅值；fmpq为对应第n+1级啮合频率.

1.5 装配相位关系

为完善系统的整体系统动力学模型，需要确定两级传动系统的装配相位关系，建立坐标系如图5所示，传动系统第二级的弹性啮合力具体形式见文献[14].

图5 两级啮合相位关系示意图

1.6 单元组装

在建立各单元模型和载荷矢量后，即可进行矩阵的组装.按照每个单元的局部节点编号，将子矩阵组装到整体矩阵中的相应位置.在同一自由度上，具有相同编号的不同单元矩阵子块需进行耦合与叠加，装配时不必进行坐标转换，单元组装形式见文献[11].

系统整体的动力学微分方程为：

其中：M为系统的质量矩阵；C为系统的阻尼矩阵；

K(t)为系统的刚度矩阵；T为系统的外部扭转激励；Fu为系统的质量不平衡激励.

采用Rayleigh阻尼计算系统单元组装时的粘性阻尼，其具体形式如下：

其中：α0、β0分别为Rayleigh阻尼的比例系数.

2 固有特性分析

两级齿轮传动系统中的轴、齿轮、轴承的结构及详细参数的选取与上一节相同.由式（8）可得系统自由振动微分方程为：

由于阻尼项对固有频率的影响较小，当转速为0 r/min时，则由式(10)可得系统的无阻尼振动微分方程为：

式(11)满足：

其中：ξi为第i阶模态的特征向量；ni为第i阶固有频率；t为时间.

在转速为0 r/min时，求解系统的前十阶固有频率见表1，系统典型振型图如图6所示.

表1 系统前十阶固有频率

图6 典型振型图

由图(6)可知，系统耦合形式分为扭转与扭转耦合、弯曲与扭转耦合和两级弯扭的复杂耦合形式在每种振型下，耦合振动形式、振动方向和主振型各不相同.

对于两级齿轮传动系统而言，耦合的形式除了单级传动系统中的弯扭、扭扭等形式，还有不同级传动之间的互相耦合，因此对于多级齿轮传动系统的固有特性进行具体分析显得尤为重要.

3 啮合特性分析

3.1 齿侧间隙的影响

由于齿轮正常工作的需要，齿轮传动系统一般必须留有齿侧间隙，本节研究齿侧间隙对系统啮合特性的影响.仿真参数设置第一根轴转速500 r/min，系统的输出扭矩为100 N·m；为单独研究齿侧间隙的影响，各齿轮几何偏心量选取为0 μm，齿轮初始偏心相位角为0°，选择三种不同的齿侧间隙情况进行分析，第一级啮合力的时域图和频谱图如图7、图8所示.

图7 不同齿侧间隙下第一级啮合力时域图

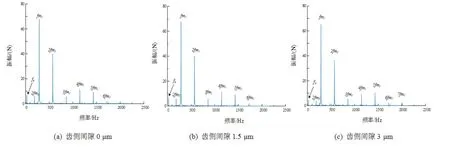
图8 不同齿侧间隙下第一级啮合力频谱图

随着齿侧间隙的增加，传动系统第一级啮合力在逐渐减小；频谱中引起峰值的各倍频成分对侧隙的增加敏感程度不同，其中第一级啮合频率的五倍频随着侧隙的增加，峰值也在随之缓慢增加，而第一级啮合频率的四倍频随着侧隙的增加，峰值却在逐渐降低.

含齿侧间隙的齿轮在工作时，会发生脱齿，整个啮合过程变成接触、分离再接触的一个反复过程.模型中计算的啮合力是由沿着啮合线投影的位移矢量推导而来，并未计入振荡产生的冲击.

齿轮传动系统的振动响应不仅和齿侧间隙有关，也与系统的转速密切相关，计算并比较不同齿侧间隙下第一级啮合力波动幅值随转速变化曲线如图9所示.可以看到，随着齿侧间隙的增加，系统第一级啮合力波动幅值在降低；转速越高，不同齿侧间隙的啮合力波动幅值差异越大.

图9 第一级啮合力波动幅值随转速的变化

侧隙的增加，导致系统脱齿的时间变长，进而在齿轮的啮合过程中产生了更多的振荡和冲击，由于在转速1 kr/min、2 kr/min、3 kr/min、4 kr/min附近产生较高的振动峰值，分别计算在不同齿侧间隙、在上述转速下的脱齿时间占整个啮合过程的时间百分比见表2.

表2 不同转速时不同侧隙下的脱齿时间百分比

可以发现，在转速相同时，齿侧间隙越大，啮合过程中脱齿时间的占比越高，这是由于侧隙的增加会导致啮合过程中的振荡冲击变大，从而脱齿的时间也会增加；在侧隙相同时，随着转速的增加，脱齿时间呈先升高后降低的趋势.这说明由于存在齿侧间隙，转速较低时系统运行并不平稳，随着转速的增加，系统运行逐渐平稳，脱齿时间也相应减少；而在到达较高转速之后，侧隙的增加使得系统啮合过程的稳定性超出了系统对外界波动的动态适应能力，对系统运行的平稳性产生巨大的影响.

3.2 偏心量的影响

设置第一根传动轴恒定转速500 r/min，系统输出扭矩为100 N·m；各齿轮选取相同的几何偏心量，齿轮初始偏心相位角为0°，齿侧间隙设置为0 μm，分别研究不同的齿轮偏心量时，系统在平稳工况下，不同的齿轮偏心量对系统两级啮合力的影响如图10所示.

图10 不同的齿轮偏心量对系统两级啮合力的影响

系统的两级主动轮、从动轮均偏心时，由于第二级啮合中传动轴的转速比第一级啮合中的转速要小得多，因而第一级啮合力对偏心量的改变更为敏感.系统各级传动的最大啮合力、平均啮合力及啮合力RMS值亦随齿轮偏心量增长而增加，说明齿轮偏心量的增加，使得系统各级传动啮合过程中的平稳程度降低，此规律同文献[16]基本一致.

为深入讨论不同偏心量对系统各级啮合力的影响，系统工况及参数不变的情况下，设置偏心量10 μm到50 μm，绘制系统两级啮合力的三维频谱如图11所示.

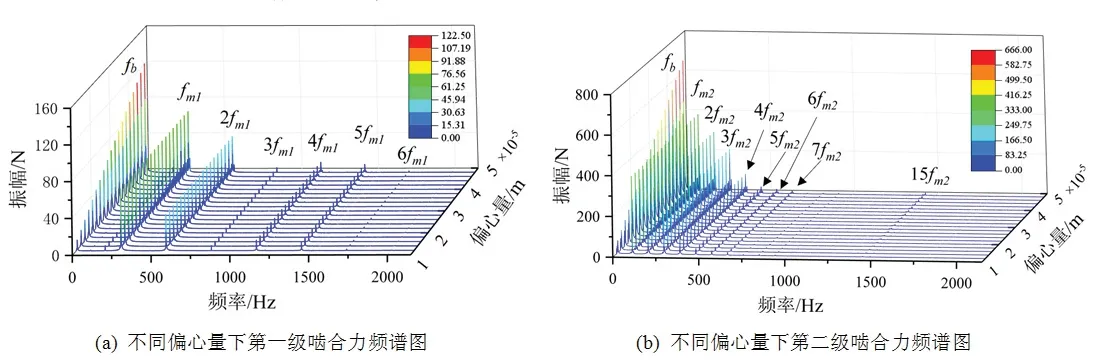
图11 不同偏心量下系统两级啮合力三维频谱图

可以看到，随着各齿轮偏心量的增加，在第一、二级动态啮合力的三维频谱图中，计入时变刚度轴承的通过频率fb引起的振动峰随齿轮偏心量的增加而增长，其他频率成分为啮合频率fm1、fm2及其倍频成分，则几乎不受齿轮偏心量增加的影响.此外，随着偏心量的增加，第一、二级啮合力频谱中以齿轮转频成分为主的附加脉冲幅值增大，产生较为显著的调幅振动.

以上结果表明，随着系统各级齿轮偏心量的增加，齿轮几何偏心量越大，系统的两级啮合力呈现出的波动越剧烈，转频成分振动幅值也随之增大并逐渐在振动成分中占主导地位，边频调制现象也越来越明显，在齿轮传动系统的设计及加工阶段，需对此加以注意.

4 结 论

本文以两级齿轮传动系统为研究对象，采用有限单元离散化的建模方法，建立了考虑齿侧间隙及齿轮几何偏心的两级齿轮传动系统动力学模型，并分析了系统的固有特性，讨论了齿侧间隙和齿轮的几何偏心对系统啮合特性的影响，得到如下结论：

（1）齿侧间隙对齿轮传动系统的啮合过程具有明显的影响，选择合适的齿侧间隙，可以减少啮合冲击，提高系统运行的平稳性.

（2）减小齿轮的几何偏心可以有效抑制啮合力的波动，在齿轮的设计加工阶段应尽可能的避免几何偏心的出现.