数形结合，让体验充盈课堂

喻菊

一、教学分析

（一）内容与学情的契合

“数与形”是人教版小学数学六年级上册数学广角的知识内容。儿童思维以具体形象思维为主，数形结合思想在小学阶段得到广泛应用，它使很多抽象的数学问题直观化、生动化，将抽象思维以形象思维的方式呈现与应用，提高了学生学习的兴趣，也有助于学生把握数学问题的本质。

六年级学生对数形结合其实并不陌生，数形结合思想一直伴隨着他们的数学学习，并已经积累了一定的活动经验。本节课的学习不在于掌握某个具体知识内容，而是要进一步渗透数形结合思想，理解数形结合的本质，掌握数形结合的方法，有意识地运用数形结合的方法解决问题，逐步发展学生抽象思维，提升学生数学素养。教师要从数学思想的角度把握教材内容的本质，更加深入地解读教材，从关注技能转向关注能力。

（二）教学目标

1.让学生经历观察、猜想、验证、归纳等活动，以形助数，以数辅形，发现规律，培养学生数形结合的意识。

2.通过动手摆小方块表示数，感悟以形助数、以数辅形的重要性，积累数形结合解决问题的活动经验。

3.体验数形结合数学思想方法的价值，感受数学的魅力。

（三）教学重点与难点

由“数”思“形”，由“形”表“数”，借助数形结合思想方法，多角度地解决数学问题，深化数学思维。

二、教学过程

（一）计算挑战——引出课题

师：听说咱们班同学的计算能力都不错，敢接受我的挑战吗？

（课件依次出示：1+3、1+3+5、1+3+5+7、1+3+5+7+9+11+13+15+17，学生计算的速度由快到慢，答案也由确定慢慢地不确定起来。在计算最后一道题时，学生给出的答案有的是49，有的是81。计算方法有的是不断连加，有的是凑整）

师：老师这里还有一个好方法，只要看一眼这个算式，就能立马知道答案，你们相信吗？

师：我们先来观察这类题有怎样的共同特点？

生：都是连续的奇数。

师：而且都是从几开始的？

生：1。

（教师板书：从1开始的连续奇数的和）

师：谁来给老师出题？有计算器的同学负责验证，看看老师是否算对了？

生：1+3+5+7+9+11+13+15+17+……+99=？

（教师快速报出结果2500，学生验证无误）

师：对于刚刚这样的计算，老师这样的速度，你们有什么想说的吗？

生：太快了！

师：其实，老师刚刚看到这些算式、这些数时，脑中想到的是一些图形。将数和形相结合，就能很快地帮助我们找到答案。你们肯定很好奇，老师脑中想的是一个什么样的图形呢？这就是我们今天要研究的内容。（板书：数与形）

【思考】在“计算挑战”中，问题从易到难，学生解答问题由快到慢。当已有的知识技能不能更好、更快地解决问题时，教师的“表演秀”就轻松地调动了学生的学习欲望，这时再介绍解决问题的新途径——数形结合，激发了学生学习的兴趣。

（二）活动操作——发现规律

师：我们就从简单的1开始。看到1，你们能想到什么图形？

生：1个长方形、1个正方形……

师：我们用1个正方形来表示1。

1.活动探究：1+3

活动要求：利用小正方形拼成一个大一点的图形来表示这个算式，并且有利于算出总数。先独立思考，再把自己的想法和同桌进行交流。

学生取出学具袋，可以把小正方形贴在黑色卡纸上，学生独立操作，教师巡视并找出具有代表性的作品进行交流评价（如图1）。

大多数学生认为第（4）个图形不仅可以直观地表示出算式，而且有利于计算出正方形的个数。

师：现在1+3可以怎么算？

生：2的平方。

师：很有意思。原来我们看这样的一个算式就只是一个算式，看这样的一个图形就只是一个图形，这节课我们用不同的眼光，发现算式借助图形的表达找到了新的计算方法，这就是数形结合思想。

2.活动探究：1+3+5

活动要求：利用手中的小正方形再拼搭成一个大一点的图形来表示这个算式，并列出算式计算出结果。

学生再次拼搭，教师选择两组具有代表性的作品进行交流（如图2）。

学生先汇报拼搭的过程，一致认为②号图形的拼搭很有规律。②号图形按“┐”形拼搭逐渐变成更大的正方形。

师：现在看着这个大一点的正方形，你们能列一个加法算式吗？

生：1+3+5。

师：它的结果可以怎么计算？

生：3的平方。

师：刚刚是2乘2，现在是3乘3，2和3是怎么确定的？

生：小一点的正方形边长是由2个小正方形边长组成的，所以边长是2;大一点的正方形边长是由3个小正方形边长组成的，所以边长是3。

生：原来是2个加数，所以它的边长是2;现在有3个加数，所以它的边长是3，就（比原来）增加了一层。

师：顺着思路继续想，我想在此基础上拼搭一个更大一点的正方形，需要增加几个这样的小正方形？

生：7个。

师：增加在哪里？比画一下。

（学生书写“┐”）

师：看到这样的一个图形，可以帮我们解决一个怎样的加法问题？

生：1+3+5+7。

师：它的结果怎么算呢？

生：看作4乘4等于16。

师：4是什么意思？

生：4是加数的个数。

生：4是正方形的边长。

师：我们从数的角度来看1+3+5+7=16，4×4=16，所以1+3+5+7=4×4。从形的角度来看，也可以发现1+3+5+7=4×4。

3.巩固提升：1+3+5+7+9

师：不拼搭，你脑中能想象出一幅图吗？是一幅怎样的图？

生：能想象出一个5乘5的正方形。

师：算式的结果可以怎样算？

生：5乘5，5的平方是25。

师：通过刚才的探究，你们找到解决这类算式的办法了吗？

生：从1开始连续奇数的和等于这些奇数个数的平方。

（師生进行举例验证）

师：“1”能写成这样的算式吗？（板书：1=12）

师：他们的总结，给我们找到了解决这一类问题的诀窍：从1开始的连续奇数的和等于这些奇数个数的平方。

【思考】人教版小学数学六年级上册“数学广角——数与形”中的例题编排是先呈现一组“形”，再辅以“数”来发现图形变化中蕴含的规律，从而达到数形结合的点睛之处。在教学这节课时我们反其道而行之，先有数，从“数”到“形”，借“形”表“数”，通过思考“怎么摆算得结果最快？”引导学生对“形”进行优化，发现“形”的规律，即几个连续奇数的和用小方块按“┐”形逐层摆放可以拼搭成一个大正方形，不仅能清楚地表达数，而且计算总数也很方便。发现“数”的规律，原来求几个连续奇数的和除了可以用加法计算，还可以用奇数个数的平方进行计算。在这个学习过程中，学生在不知不觉中就借助“形”来思考“数”的问题，而“数”的问题在“形”的辅助下又产生了新的解决方法。

（三）实践尝试——问题解决

1.1+3+5+7+9+11+13+15+17=？

师：回到口算挑战的最后一题，你们脑中有图吗？它是一个什么样的图？

生：是边长为9的正方形。

师：可以快速地算出总数吗？是多少？

生：9×9=81。

师：和之前“凑整法”比较，你们觉得有什么想说的？

生：更简单了。

2.1+3+5+7+5+3+1=？

学生思考发现，可以将算式分成1+3+5+7和5+3+1两部分，想象出图3，再运用结论进行计算。

师：规律总结出来，还可以这样灵活着用。

3.5+7+9+11+13+15+17=？

学生把算式看成1+3+5+7+9+11+13+15+17-（1+3），抽象出图4，即从边长为9的正方形中减去一个边长为2的正方形。

师：太了不起了，在短时间内脑海中有了这么多的图形帮助我们解决数的问题。

4.2+4+6+8+10+12+14=？

师：一开始我们研究的是连续奇数的和，现在应该怎么思考？

生：我们可以将算式中的每个数减掉1，他们又回到了1+3++5+7+9+11+13，然后先算出7的平方，再加7，结果等于56。

师：还有没有别的方法？

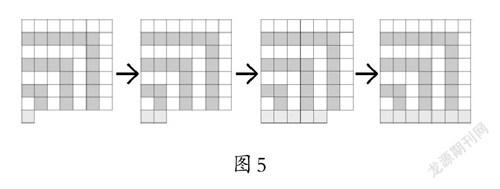
课件逐步演示正方形演变成长方形的过程（如图5）。

师：7个1就全部补在哪里？

生：正方形的下面。

师：现在你们看到的是一个什么图形？

生：拼成了一个长为7、宽为8的长方形。

师：可以快速地算出它们的和是多少吗？

生：长方形中有56个小正方形，所以和是56。

师：真好，我们从连续奇数的探究到连续偶数的探究都给解决了，了不起。

5.1+3+5+7+9+11+13+15+17+……+51=？

师：有人觉得难了，它难在哪儿啊？

生：个数没法确定。

师：咱们碰到难题时要知难而进。

师：知难而进，进的确是一种勇气。有的时候知难而退更是一种智慧，但是这个退不是不做，退一退，是从简单入手，找到它的突破口。

学生结合课件观察算式1+3+5+7+9+11中加数的个数6与奇数11之间的关系，最终发现：（最外圈数+1）÷2=正方形边长（如图6所示）。

师：现在咱们找到了解决问题的关键步骤了。算式的个数怎么确定？

生：51加1再除以2，得26。

师：1+3+5+7+9+11+13+15+17+……+51=262。

【思考】本节课的练习中既有基础训练，又有变式训练。教学中，教师有意识地追问学生“脑中有图吗？”“脑中有什么样的图？”，学生脑海中的图形也渐渐地随着数的变化而发生变化。由1个正方形，到出现2个组合的正方形，再到有空缺的正方形;又从正方形到长方形，从“形”中觅“个数”……学生在这样的练习中，将数与形紧密地结合在一起，有数就有形，形中能见数，同时练习的精巧设计打破了学生对数与形的认知局限，数变形亦变，数形结合思想在学生的脑海中生根发芽，学生对原有的概念认知赋予新的理解。

（四）拓展延伸——沟通联系

1.在以往的学习中，大家有没有数形结合的经验？（播放微视频）

2.图形判断（如图7）。学生发现图形的表达要借助数据才更加精准，从而感悟数学数形结合的魅力。

师：难怪数学家华罗庚爷爷这样说：数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休。

【思考】本课的最后，教师通过举例说明数形结合无处不在。在小学阶段的数学学习中，我们可以借助图形来认识自然数、小数和分数，在图形的帮助下学习加、减、乘、除四则运算，在一些图形面积公式的推导过程中，数与形也是紧密相连的。在位置与方向的学习中，数形结合能准确定位，枯燥的数据用统计图表直观地表示出来，方便进行数据分析和决策。离开课本，大自然里也有神奇的数与形。从含苞待放的花朵到玫瑰花瓣，再到植物的种子，数都无处不在。最后借助华罗庚的诗词让学生品味数形结合思想，让学生的数学学习变得更加有意思。

（作者单位：江西省南昌市湾里管理局教科体局教研室）

投稿邮箱：405956706@qq.com