情境问题解决中的学生认知发展

夏小刚 邓清

夏小刚

贵州师范大学数学科学学院教授、博士生导师、副院长，教育部高等学校数学类专业教学指导委员会委员;已在《比较教育研究》《数学教育学报》《人民教育》《民族教育研究》《课程·教材·教法》《数学通报》《Journal of Mathematics Education》等期刊发表“数学情境的创设与数学问题提出”等论文，出版《基于提出问题的数学教学研究》等著作;曾获国家级教学成果一等奖等奖励，以及贵州省高等学校教学名师、贵州省优秀教师等荣誉称号。

随着新课程改革的不断深化，我国数学教育已逐渐从注重知识的掌握发展到注重基于情境问题解决的数学素养培养。为此，我们需要对情境问题解决中的学生认知发展情况做必要的分析和反思，以探寻面向核心素养培养的数学教学的切入点，为教师有效实施问题解决教学提供参考。

一、调查设计

20世纪90年代末，蔡金法教授以贵阳市小学五年级学生为研究對象，对中美学生在数学情境问题中的认知表现做了一系列的实证研究。为了研究近20年来我国五年级学生在情境问题解决中的认知发展情况，笔者选用了与蔡金法教授所选的同样的6所公办学校的五年级学生为研究对象。其中3所学校教育质量高于贵阳市平均水平，另外3所处于贵阳市平均水平。笔者从每所学校选取中等水平的一个班的学生进行测试，得到有效问卷276份。

测试采用了蔡金法教授编制的3份问卷。卷一涉及18个较为简单的情境问题，卷二和卷三分别涉及6个较为复杂的情境问题，其中卷二的问题属于过程受限问题，卷三的问题属于过程开放问题。这3份测试卷的信度系数分别为0.78、0.66和0.72。

二、调查结果与分析

1.问题解决结果差异性与均衡性并存

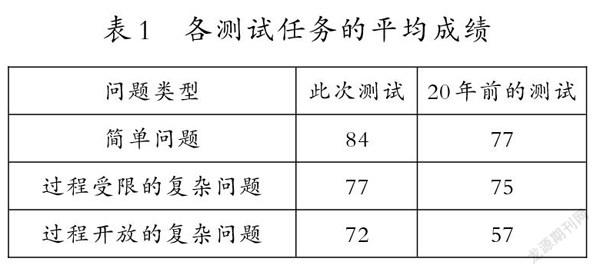
表1显示了学生在较为简单的情境问题（简称“简单问题”）、过程受限的复杂的情境问题（简称“过程受限的复杂问题”）和过程开放的复杂的情境问题（简称“过程开放的复杂问题”）上的数学表现。

由表1可见，学生在简单问题（t=6.60，p<0.001）、过程受限的复杂问题（t=2.12，p<0.05）和过程开放的复杂问题（t=14.22，p<0.001）的解决上，得分均高于20年前，且差异显著。学生在3个测试任务上的数学表现各有不同，但与20年前相比，这种差异已明显减小，且呈现相对均衡的发展状态。

2.问题解决策略体现多样性和创造性

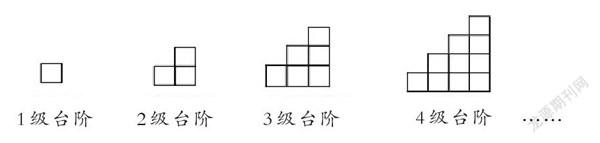
学生在解题策略上几乎与20年前的情况一致，即大部分学生都采用了常规策略。此外，有不少学生采用了非常规性解题策略，有的解题策略是在20年前的测试中没有出现的。如“台阶问题”，学生被要求根据下图求20级台阶的方块数。

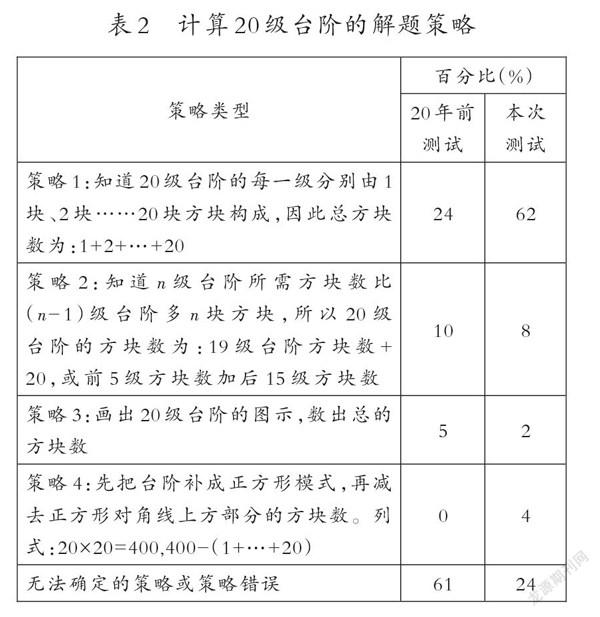
笔者用表2呈现了两次测试中学生计算20级台阶所使用的解题策略。

可以发现，本次测试中有76%的学生采用了恰当的解题策略，这一比例明显高于20年前（39%）。采用恰当解题策略的学生中，能正确求出方块数的占比为78%（20年前为38%）。在正确求解的学生中，62%的学生使用了“高斯方法”，这一比例也明显高于20年前（30%）;还有少数学生采用了“画图计数”策略（如表2中策略3）以及“添补”策略（如表2中策略4）。由于“添补”策略是先把阶梯形添补为正方形，再从所得到的方块总数中减去后添加的方块数，所以这种解题策略抽象度更高。

3.符号表征是主要表征模式

统计结果表明，近20年来采用符号表征的学生占比最多。这在一定程度上反映出学生已经从“直观思维”过渡到了算术思维，甚至是代数思维。以“帽子问题”为例，该问题以图示方式呈现了某商店在第一个星期、第二个星期和第三个星期所售出的9顶、3顶和6顶帽子，问这家商店在第四个星期应该卖多少顶帽子，才能使售出的帽子平均数为7。笔者统计了学生表征“帽子问题”的模式（见表3）。

从表3中可以发现，学生两次解决“帽子问题”时，都主要采用算术符号表征（如9+3+6=18，4×7=28，28-18=10）或代数符号表征（如设第四个星期卖出x顶，由“（9+3+6+x）÷4=7，可知x=10”）。但值得关注的是采用代数符号表征的学生比例明显减少，采用算术表征的学生比例明显增加。这一现象值得我们做进一步研究。

4.缺乏对概念性知识的理解

测试中有两个关于平均数的情境问题。一是“春游问题”（T1）：某小学师生共296人，准备乘车去春游，如果每辆车能坐24人，共需要多少辆车。二是前面提到的“帽子问题”（T2）。前者涉及平均数算法知识的运用，后者体现了对平均数概念的理解。

表4数据显示：两次测试中，能正确解答“春游问题”的学生占比均在85%以上，而能正确解答“帽子问题”的学生占比为61%，后者占比明显低于20年前（71%）。笔者对学生解决“帽子问题”的3种典型错误进行统计，发现近70%的解题错误涉及平均数概念的理解，如有的学生用前三周所卖的帽子数18除以3，得到6，但是题目中所指的平均数是7，便在前三周的和的基础上加3，然后除以3，得7，于是错误地给出答案“3”。这表明近20年来，学生虽然较好地掌握了平均数的算法，但对平均数的概念性理解水平相对较低，甚至有所下降。

三、调查结论与建议

总体来看，近20年来情境问题解决中的学生认知发展情况呈现以下特点：一是学生解决过程开放的情境问题的能力进步明显;二是学生解决情境问题的策略更具多样性和创造性;三是在多种表征共同发展的基础上，符号表征仍然是学生运用的主要表征模式;四是学生缺乏对概念性知识的深度理解。据此，笔者提出以下建议。

第一，注重情境问题的创设。经过20年的发展，学生解决简单问题和复杂问题的能力均得到提高，特别是在解决过程开放的复杂问题方面的进步更为明显。无疑，在基础教育课程改革背景下，基于情境问题的教学对学生问题解决能力的提升产生了积极作用。但是我们也看到，学生在非常规问题解决上的数学表现不如常规问题，在复杂情境问题解决上的数学表现不如简单问题。这说明复杂的、非常规的情境问题依然影响和制约着学生对数学问题的分析和解决。为此，教师要注重情境问题的创设。具体来说，在新知引入阶段，情境问题的创设应采用学生熟悉的、有利于知识生长和发展的数学情境;在知识应用教学中，情境问题的创设应具有现实性、层次性和开放性，问题的现实性有利于学生从数学的角度观察和思考问题，问题的层次性有利于不同水平的学生发展数学思维，问题的开放性有利于学生数学综合能力和创新意识的发展。

第二，鼓励学生用多种策略解决问题。本次测试，无论是结果还是过程，学生在过程开放的情境问题解决上的数学表现明显好于20年前。然而，我们也发现仍有较大比例的学生未能根据自己的理解建构恰当的解题策略，甚至放弃问题的解决。在一定层面上，这与下列原因有关：实践中，教师对学生的自我建构特别是偏离教学目标的数学理解，存在明显的认识偏差，比如在“列方程解决问题”中，教师对学生采用的算术策略或试误策略大多不给予积极评价，尽管学生采用这样的策略也能做出正确的解答。无疑，教师需要关注和鼓励学生采用多样化的解题策略，注重学生数学自我认识的建构，激发学生的探究意识，使他们在面对复杂问题时勇于探索，进而发展创新精神，提升实践能力。

第三，注重学生数学直观与数学抽象思维的平衡发展。研究表明，学生在解决情境问题时，大多采用较为抽象的解题策略和符号表征，较少使用言语推理策略或视觉表征方式。这符合对小学五年级学生数学认知发展的基本要求，也体现了学生数学思维能力的发展。然而，也有不少采用抽象表征的学生并未正确解决问题，且不少基础较差的学生不会采用较为简单、直观的表征方式。为此，教师要把握学生数学直观与数学抽象思维的平衡。以“帽子问题”为例，学生的解题错误主要在于对符号表征的盲目使用。事实上，换用图示表征（如下图），通过“割补”方式解决问题更简便。

直观与抽象是数学发展的两翼。波利亚说：“抽象的道理是重要的，但要用一切办法使它们看得见，摸得着。”因此，教师应鼓励学生通过图示表征等较为直观的方式，将复杂和抽象的数学对象简明化、具体化，促进学生数学素养的发展。

第四，注重学生对数学知识的概念性理解。有研究指出，数学概念是从具体情境或数学情境中舍去事物的非本质属性，保留本质属性而抽象出来的。调查结果反映出学生对平均数本质理解的缺失，因此，教师不仅要引导学生体会“是什么”，而且要注重概念的多元表征，如实物表征、图像表征、言语表征、符号表征等，训练学生转换不同的表征方式，促进学生对概念本质的认识和对知识的有效运用。

（邓清，贵阳市乌当中学）

[本文系全国教育科学“十三五”规划课题“面向核心素养的数学问题情境教学测评模型研究”的研究成果。课题编号：XHA180286]

责任编辑  刘佳