某大跨度钢管混凝土拱桥行波效应分析
2022-02-12周胜
周胜
(长沙理工大学 土木工程学院,湖南长沙 410114)
0 引言
随着材料和施工技术的进步,桥梁跨度越来越大,受传播路径、介质构成和局部场地等因素影响,地震动时空分布并非一致。对于尺寸较小的桥梁,地震动的空间变化很小,可采取一致激励模式进行分析,然而对于一些尺寸较大、跨度较大的桥梁,或其它无法忽略地震动空间变化影响的桥梁,除了考虑一致激励的方法外,还需要考虑结构空间变异的问题,需采用非一致激励或者多点激励的方式进行地震响应分析[1]。
地震时,从震源释放出来的能量以地震波的形式传至地表,导致地表各点接收到的地震波是经由不同路径、不同地形地质条件而到达的,因而地表的振动必然存在差异。这种差异主要包括以下几个方面:一是在地震动场不同位置,地震波的到达时间存在一定的差异,称之为行波效应;二是地震波在传播过程中,会产生复杂的反射和散射,因此地震动场不同位置地震波的叠加方式不同,导致相干函数的损失,称之为部分相干效应;三是波在传播的过程中,随着能量的耗散,振幅也会随之减小,称之为波的衰减效应;四是地震动场不同位置,土的性质存在差异,导致地震波的振幅和频率受到影响,称之为局部场地效应。目前,考虑到结构的空间变异,主要采用行波法,即不同支撑点给予不同的地震波,或给予地震波到达桥梁支撑点的时间延迟[2-4]。
1 计算模型介绍
某特大桥主梁中心桩号为K18+717,起点桩号为K18+511,终点桩号为K18+923,桥跨布置为(2×35+252+2×35)m上承式钢管混凝土拱桥,主桥桥面系为(13×20)m先简支后桥面连续T梁;两侧引桥均为2×35m预应力混凝土先简支后桥面连续T梁,桥梁全长412m。主拱由两条拱肋组成,拱肋为等截面四管桁式构件,拱肋拱轴线采用悬链线,主桥长260m,计算跨径L=252m,矢高f=45.82m,矢跨比为1/5.5,拱轴系数m=1.167。大桥桥型的立面布置图如图1所示。全桥共3386个节点,7033个单元,有限元模型如图2所示。
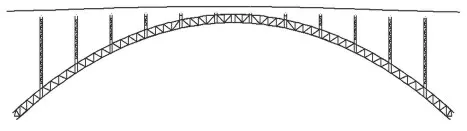
图1 大桥桥型立面布置图

图2 有限元模型图
1.1 主拱
拱肋结构设计为等截面四管桁式结构,拱肋高5.0m,宽2.7m,上、下弦管皆为直径1100mm的钢管,桥梁横向设置两个拱肋,拱肋中距9.3m。上弦管壁厚由拱脚向拱顶分别为26mm、22mm、26mm,下弦管壁厚由拱脚向拱顶分别为26mm、22mm、18mm,管内灌注C55自密实补偿收缩混凝土。单个桁架各弦管之间竖向通过直腹杆、斜腹杆连接,横向通过横缀管连接。直腹杆、斜腹杆都采用Φ508×16mm钢管,横缀管采用Φ711×16mm钢管。拱肋节段划分按最大吊装重量不超过100t控制,节段间接头及合龙段在吊装阶段通过上、下弦管内设置的内法兰临时栓接,待拱肋合龙并调整拱轴线形后再将接头钢管焊接。拱脚弦管与拱座预埋钢管间采用外包弧形钢板围焊连接。
1.2 拱上立柱
拱上立柱采用钢管混凝土和空钢管排架。其中1#、2#、11#、12#四个较高立柱采用的钢管直径为457mm,壁厚为10mm,立柱内灌C55自密实补偿收缩混凝土,其余立柱采用的钢管直径为406mm,壁厚均为10mm,空钢管。主管间纵横向平联管采用的钢管直径为219mm,壁厚6mm,其内不灌混凝土。
2 动力特性计算与分析
2.1 动力特性计算
结构的动力特性分析是地震响应分析的基础,它能够反映结构自身固有的振动特性。根据结构动力学计算公式可知,结构的自振频率主要与质量、刚度和阻尼比有关。因此,正确求解桥梁结构的动力特性,在桥梁结构的动力分析计算中占极其重要的地位,尤其是前若干阶自振频率和振型模态分析更为重要,因为其在结构的抗震分析计算中起控制作用。本文采用多重Ritz向量法,利用通用有限元软件MidasCivil2020对模型进行自振特性分析,并计算出了桥梁结构的前90阶振型。表1列出了该大桥的前十阶自振周期、频率及相对应的振型特征形态,图3—图6为具有代表性的第一阶、第四阶、第六阶和第十阶振型图。

表1 拱桥前十阶自振特性表
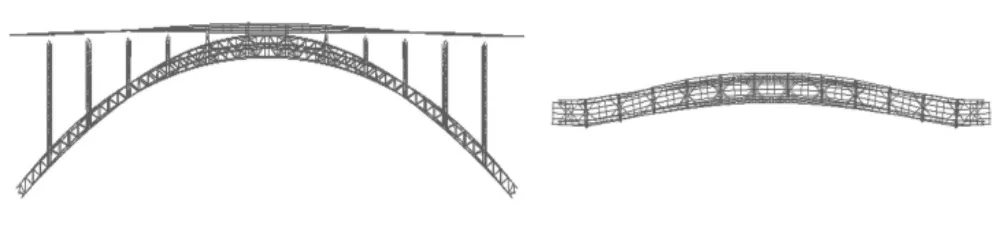
图3 第一阶振型
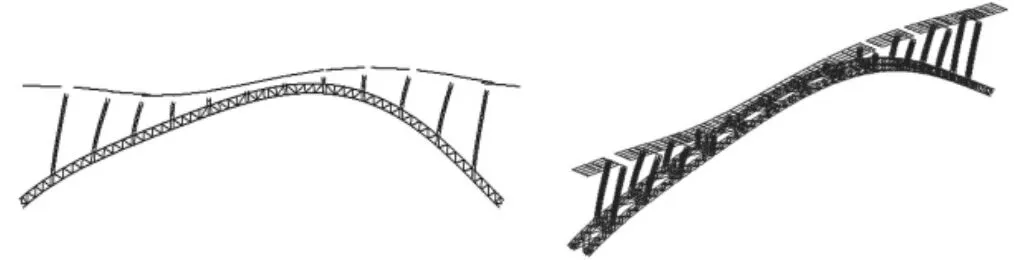
图4 第四阶振型

图5 第六阶振型

图6 第十阶模态
2.2 动力特性分析
(1)该桥振型分布较为密集,模型基频为0.318008Hz,模型前10阶自振频率范围为0.318008~0.967211Hz,1阶到10阶频率差幅度小于1Hz,说明该桥整体偏柔性(刚性桥梁基频范围一般在2.5~3.5Hz之间)。这与该桥桥宽较小而跨径较大的设计形式相吻合。
(2)第1阶振型表现为拱梁横向一阶对称弯曲,频率为0.318008Hz。从前10阶振型特性来看,其中横向振型有6阶,竖向振型有2阶,横向振动问题较为突出,这表明拱肋之间横向连接比较弱,横向刚度较小,因此大跨度拱桥设计时应注意加强横向刚度。
(3)该桥首先发生拱梁面外横向弯曲,直至第4阶振型表现为拱梁竖向反对称弯曲,频率为0.586461Hz,远远大于第1阶的对称横弯频率,说明该桥结构面外振动影响要强于面内振动影响,同时面外稳定性要弱于面内稳定性。
(4)第6阶振型为拱上立柱对称弯曲,由于结构比较复杂,因此会出现局部振动,这说明拱上立柱的抗弯能力较强,稳定性较强。拱上立柱是连接主拱圈和桥面系主梁的关键部件,在前10阶振型中,两者的振动趋于相同,说明拱上立柱起到了很好的作用,提高了桥梁的整体稳定性。
3 地震波的选取与调整
一般常用三种方法选择合适的地震加速度时程记录:一是直接利用强震记录,根据建设场地的地质条件,选择符合要求的实际地震波,但通常情况下,桥梁拟建场地没有可供选择的实际强震记录,即使有实际强震记录,还需对实际地震波进行幅值或周期的修正;二是规范化的经典地震波,常用的经典地震波有EICentro波(埃尔森特罗波)、Taft波(塔夫特波)、天津波等,可根据桥梁实际场地条件选取合适的地震波;三是人工合成地震波,人工拟合地震波主要根据规范设计的反应谱拟合而成,或者根据建设场地的基岩参数确定频谱特性、加速度峰值和震动持续时间,尽可能真实模拟地震加速度时程[5-7]。
本文根据第二种方法,拟采用塔夫特(1952 Taft Lincoln School Vertical)的强震地震波。Taft波的特征周期=0.353s,符合反应谱的特征周期0.35s,该波设计加速度峰值为0.1048g,持续时间为54.26s。对结构进行分析处理,采用本桥设计地震烈度7度,其设计基本加速度峰值为0.10g,结构基本周期为3.145s,所以将选取的地震波峰值、周期进行调整,水平向地震波放大系数为0.95,竖向地震波取水平向地震波峰值的0.65倍,持续时间取地震波的前30s输入。
4 行波效应
本文考虑顺桥向的行波效应对该桥梁地震时程响应的影响。假设地震波沿桥梁有限元模型顺桥向从左到右传播,则地震波到达左墩的时间为0s。该桥计算跨径为252m,考虑地震波的传播速度对桥梁结构的影响更具特征性,取地震波的传播速度分别为100m/s、500m/s、1000m/s[8],表2列出了不同速度的地震波到达不同桥墩的时间差。表3—表5为行波效应下主拱圈各位置三个方向的位移峰值和顺桥向一致激励下的位移峰值,表6—表11为行波效应下主拱圈各位置三个方向的内力峰值,图7为不同波速与一致激励下的纵向位移对比图,图8为不同波速与一致激励下的竖向剪力对比图,图9为不同波速与一致激励下的横向弯矩对比图。

图7 不同波速与一致激励下的纵向位移对比图

图8 不同波速与一致激励下的竖向剪力对比图
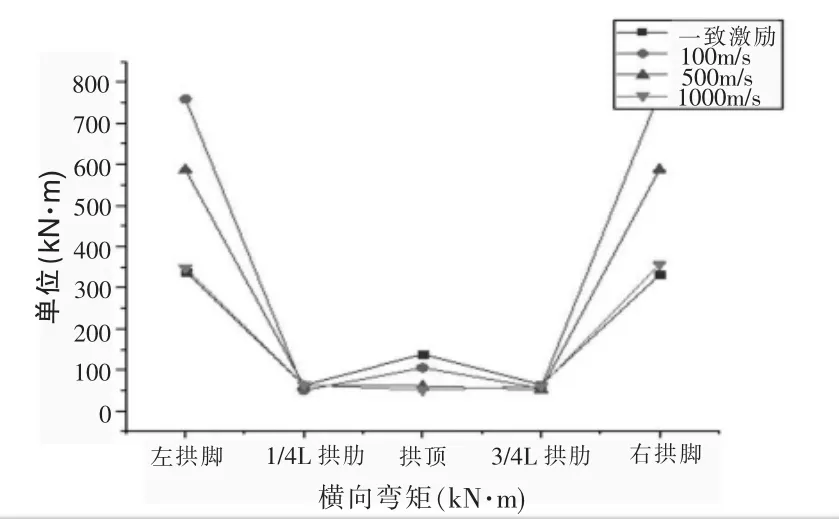
图9 不同波速与一致激励下的横向弯矩对比图

表2 不同速度地震波到达各桥墩的时间(s)
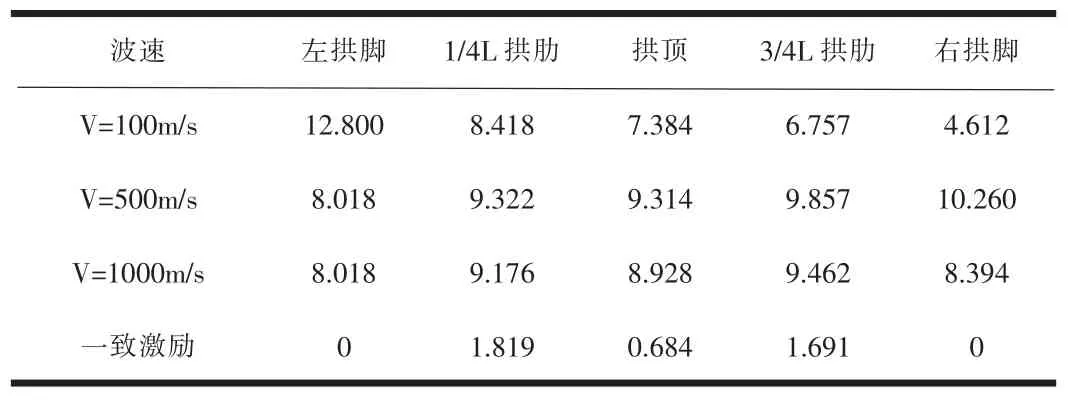
表3 不同速度地震波下主拱圈各位置最大纵向位移D×(cm)

表5 不同速度地震波下主拱圈各位置最大竖向位移Dz(cm)
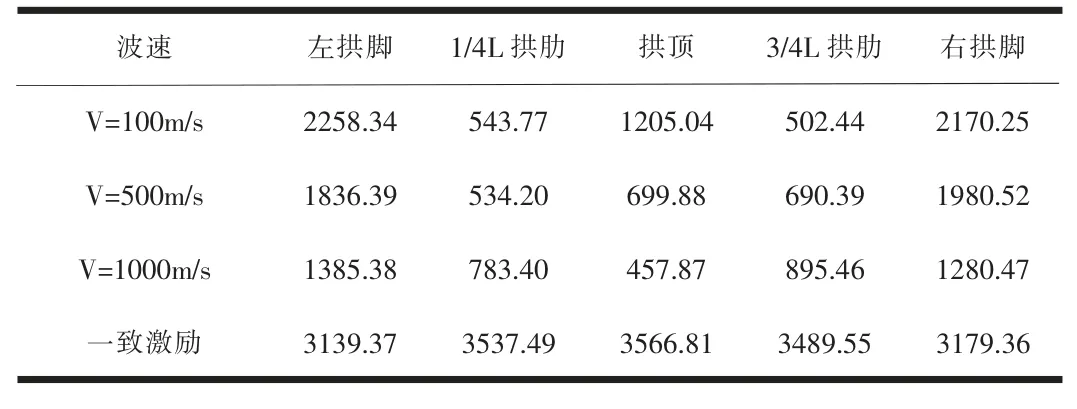
表6 不同速度地震波下主拱圈各位置最大轴力F×(kN)
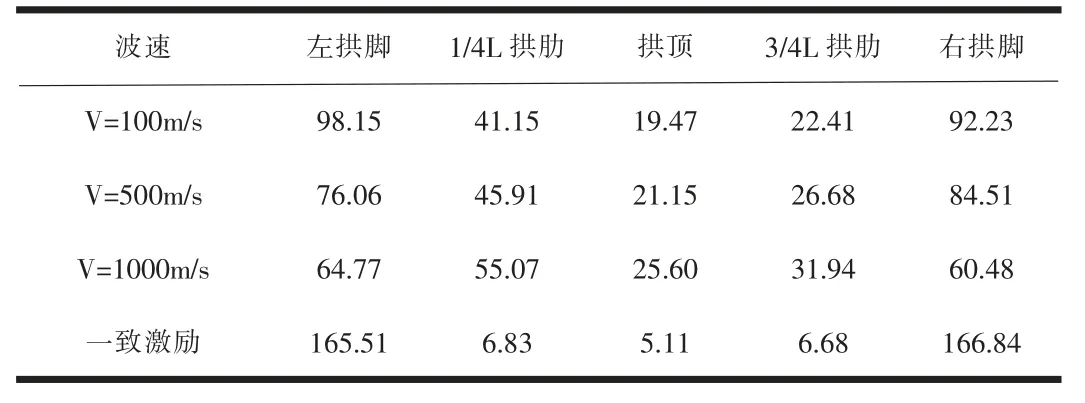
表11 不同速度地震波下主拱圈各位置最大竖向弯矩Mz(kN·m)
对表2—表5进行分析,可知:
(1)由表3可得,随着地震波速度的增加,除了左拱脚轴力有较小的减小以外,主拱圈各位置的纵向位移不断增大,当速度为100m/s时,地震作用于桥梁上的时间最长,此时主拱圈从左到右纵向位移逐渐减小,而且主拱圈纵向位移整体增幅较大,说明地震的延迟效应对纵向位移影响较大;
(2)由表4可得,随着地震波速度不断增大,主拱圈各位置的横向位移不断增大,主拱圈从左拱脚到右拱脚横向位移先减小再增大,拱顶横向位移最小,说明地震的延迟效应对横向位移影响较小;

表4 不同速度地震波下主拱圈各位置最大横向位移Dy(cm)
(3)由表5可得,随着地震波速度的不断增大,主拱圈各位置的竖向位移不断减小。主拱圈从左到右各位置位移基本呈现对称振动的趋势,且拱顶竖向位移最大。
对表6—表11进行分析,可知:
(1)由表6和表7可知,主拱圈各位置的轴力和横向剪力随着波速的增大而减小,当波速为100m/s时,左拱脚的轴力最大,随着地震波的传播,向右拱脚传播的地震波能量逐渐减小,拱顶的轴力减小到了左拱脚轴力的一半;
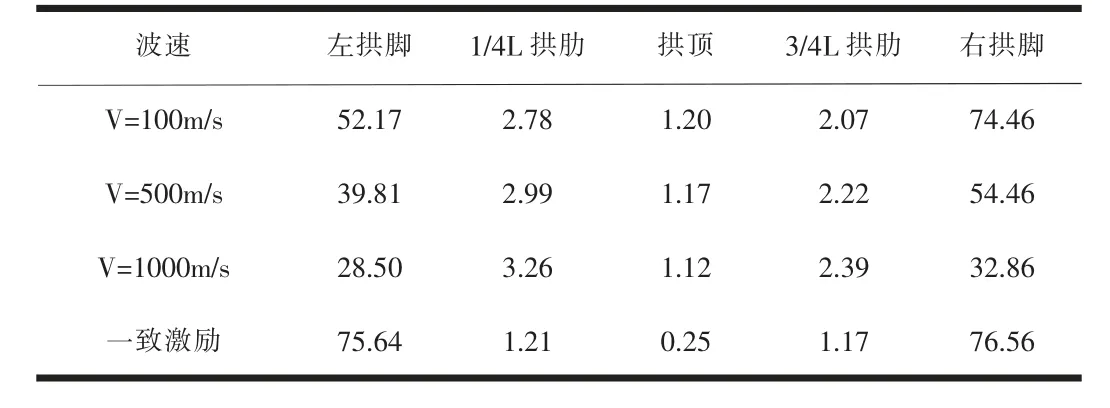
表7 不同速度地震波下主拱圈各位置最大横向剪力Fy(kN)
(2)由表8和表9可知,地震波传播速度的大小对主拱圈各位置的竖向剪力和扭矩有较大影响,其中左拱脚处竖向剪力的降幅为120.82%,拱顶处竖向剪力随着地震波传播,到了一个明显的极值,主拱圈各位置的扭矩变化相对较小;
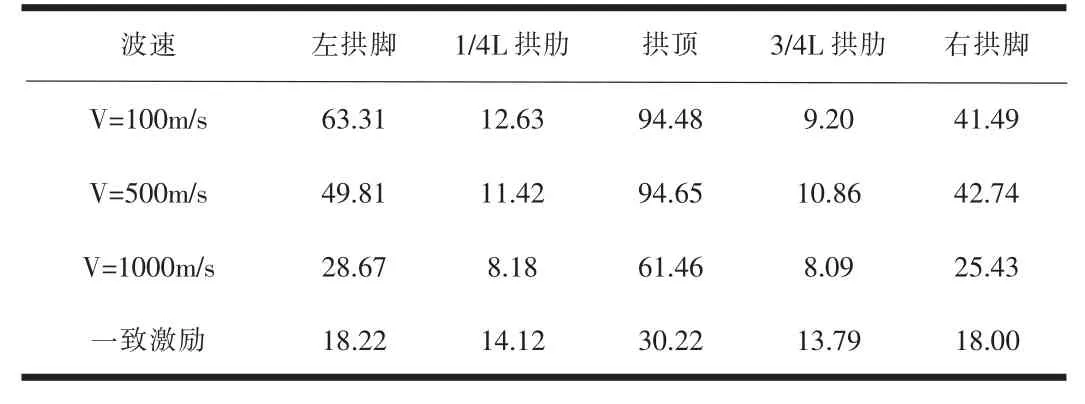
表8 不同速度地震波下主拱圈各位置最大竖向剪力Fz(kN)

表9 不同速度地震波下主拱圈各位置最大扭矩M×(kN·m)
(3)由表10和表11可知,波速为100m/s时,拱脚的最大横向弯矩为一致激励时最大横向弯矩的2.23倍。
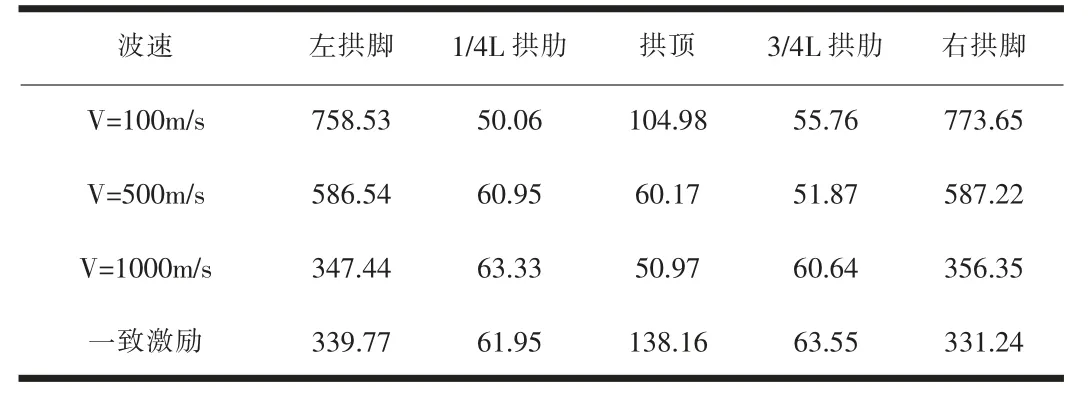
表10 不同速度地震波下主拱圈各位置最大横向弯矩My(kN·m)
从以上分析可知,随着波速的增大,主拱圈的内力逐渐减小,纵横向位移减小,竖向位移有略微增大。
5 结论
(1)波速的变化会极大地影响桥梁结构本身的内力和位移变化。
(2)与桥梁在一致激励下的结构响应对比,可以得出桥梁结构在行波效应的影响下,纵横竖三个方向的位移都大幅增加,除轴力、横向剪力和竖向弯矩有所减小以外,竖向剪力、扭矩和横向弯矩都有大幅增加。
(3)桥梁结构在地震响应的影响下,横向变形较大,设计时增加桥梁的横向刚度是提高抗震能力的有效方式,桥梁结构还可以提高整体和局部刚度、加装减隔震装置延缓行波效应对结构的影响。当桥梁跨径一定时,波速的大小决定了结构的时间迟滞效应,在讨论行波效应对桥梁结构的影响时,波速和桥梁跨径是相辅相成、成对出现的。
本文针对某特定跨径桥梁进行行波效应分析,可为该类桥梁或同跨径桥梁的抗震设计提供理论及工程实践参考。
